“四个基于”促进学生主动学习

一名学生完整认识体系的建构，能力的提高，行为习惯的养成，归根到底在于学生主动性的发挥. 那如何促进学生主动学习呢？笔者结合“复式折线统计图”的教学实践，从以下四个“基于”谈谈个人粗浅看法.

一、基于教材特点，自主阅读，理解概念

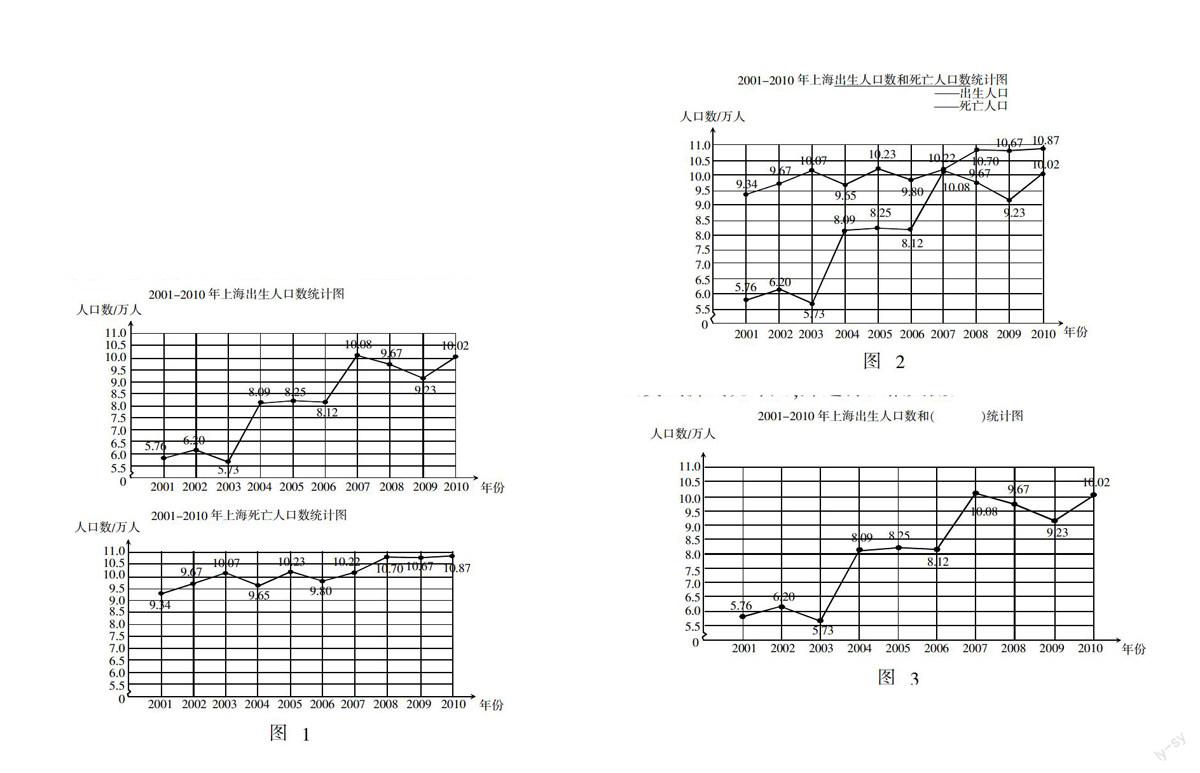
苏霍姆林斯基认为：学生学习越感到困难，他在脑力劳动中遇到的困难越多，他就越需要多阅读. 因为，阅读能激发学生的觉醒；阅读能带给学生思考，学生思考越多，他对知识的感受性就越敏锐. 例如人教版（2013版）教材五年级下册的“复式折线统计图”，当笔者在备课时，一直纠结为什么人教版（2013版）教材没有继续沿用实验版教材的例题“调查第9～14届亚运会中国韩国获金牌数情况”，而改成“调查2001-2010年上海的出生人口数和死亡人口数”. 在这个例题中，有几个专有名词把老师都给难住了. 如：人口老龄化社会、影响人口老龄化的重要影响因素、人口自然增长数、人口负增长，等等. 这几个专有名词对学生来说更是陌生. 在试教时笔者利用课堂时间给学生讲解，花掉很多宝贵时间，可学生还是似懂非懂，影响教学任务的完成. 后来笔者改变策略，把理解这几个专有名词延伸到课外，布置学生课前去查找相关资料阅读理解，课上汇报. 如此教学，大大提高学生学习的积极性和主动性. 很多老师在评课过程中都提到，这几个专有名词连老师都很模糊，如果孩子没有提前阅读，很难圆满地完成本节课的任务.

二、基于教学难点，制造冲突，突破难点

制造冲突不仅可以将新旧知识、事物关系沟通起来，而且能够培养学生学习的兴趣，活跃学生的思维，是一种非常适合突破教学难点的方法. 复式折线统计图的教学难点是让学生体验感悟将两幅单式折线统计图合并为一幅复式折线统计图的必要性. 为此，需要比较出生人口数和死亡人口数的变化情况. 为突破难点，笔者设计了如下三个问题，让学生用起立抢答的方式来完成.

1. 2006年的出生人口是多少万人？

2. 哪一年的死亡人口数最多？

3. 哪一年出生人口数和死亡人口数差距最大？

在抢答前两个问题时，全班学生在很短的时间内都起立抢答，而在回答第三个问题，过了一段时间才有两名同学起立抢答，形成强烈的对比. 此时，教师通过追问化解难点.

师：唉！为什么这道题只有两名学生会回答？

生：因为这道题有点难，它既要看上幅图，又要看下幅图，比较麻烦.

师：那你们有什么办法使它变得不再这么麻烦呢？

生：可以把这两幅图合并.

师：以前有过这样的学习经验吗？

生：以前学过复式条形统计图就是把两幅单式条形统计图合并.

师：下面请同学们试着把两幅单式折线统计图合并成一幅图.

当复式折线统计图画好时（图2），教师继续追问：现在你能很快回答第三个问题吗？生：能（学生很快说出正确答案）

通过以上环节，让学生深切感受到单式折线统计图的局限性，从而体会到学习复式折线统计图便于直观比较两组数据的变化特点，主动唤醒学生求知的欲望.

三、基于教学重点，自主探究，经历知识形成过程

《义务教育数学课程标准》（2011版）指出，在教学活动中，教师要选择适当的教学方式，因势利导、适时调控，努力营造师生互动、生生互动、生动活泼的课堂氛围，形成有效的學习活动. 学会绘制复式折线统计图是本课的教学重点，在教如何绘制复式折线统计图这个环节，笔者让学生在图3试画复式折线统计图，并进行汇报交流.

师：（教师展示学生作品：两条折线颜色一样）同学们，这两条折线，哪条是上海出生人口数？哪条是上海死亡人口数？

生：没办法看出来，因为他们颜色一样.

师：你有什么建议？

生：要用不同颜色进行区分.

师：哦！原来要用不同颜色的线区分上海的出生人口数和死亡人口数.

师：（展示第二名学生的作品：缺少图例）现在这两条折线它们颜色不一样了，你能区分哪条是出生人口数，哪条是死亡人口数了吗？

生：不能，因为没有图例.

师：（展示第三名学生作品：既区分颜色，又有图例，标题不完整）这幅图两条折线的颜色不同，也有图例，可以吗？

生：标题没写完整.

接着教师引导学生小结绘图注意事项：

1. 标题要完整

2. 要有图例

3. 要用不同颜色的线区分两组不同的数据.

师：还有不同想法吗？（展示用实线和虚线表示不同数据的画法）

最后让学生订正完善自己制作的复式折线统计图，教师再用课件演示一遍. 这样改变原有先认后画的顺序，让学生试着按自己的想法画出复试折线统计图，并在交流反馈中初步构建完整的复式折线统计图，更能发挥学生的积极主动性.

四、基于生活经验，自主分析，提高实践能力

数学对学生来说，就是利用自己的生活经验对数学现象的一种“解读”. 《义务教育数学课程标准》（2011版）指出，数学教学内容必须要选择贴近生活实际，有利于学生体验与理解，思考与探索. 与此同时，也要引导学生学会用数学的眼光去观察，分析日常生活中的事物，增强学生应用数学的意识，提高实践能力. 在本课教学时，为提高学生的分析、判断、预测能力，笔者设计了如下问题：

1. 甲乙两地月平均气温统计图.

（1）根据统计图（图4），你能判断一年气温变化的趋势吗？

（2）有一种树莓的生长期为五个月，最适宜的生长温度为7～10°C，这种植物适合在哪个地方种植？

（3）小明住在甲地，他们一家要在“十一”黄金周去乙地旅游，你认为应该做哪些准备？

此题重点是让学生进行数据分析，通过数据分析了解甲、乙两地的不同气候特点，进一步解决相应的实际问题，体会统计数据对解决问题的作用. 如根据甲乙两地月平均气温图可以确定树莓适合在乙地种植，因为乙地10月～次年3月的气温在3～11.1°C. . 根据甲乙两地月平均气温同学们可以大胆预设，小明住在甲地，他们一家要在“十一”黄金周去乙地旅游， 应该多准备一些厚的衣服，注意防寒保暖. 通过以上复式折线统计图的分析，学生做到了学以致用，发现生活中的统计应用价值，培养学生的预测能力.

课堂是学生学习场所，也是学生生活的重要组成部分，教师应该运用自己的智慧和创造力，让学生主动参与数学课堂学习活动，培养学生主动获取知识的学习能力，让课堂成为学生的智慧之旅.