一种线性校正到达时间差定位算法
朱国辉冯大政 周 延 赵海霞
(西安电子科技大学雷达信号处理国家重点实验室 西安 710071)
一种线性校正到达时间差定位算法
朱国辉*冯大政 周 延 赵海霞
(西安电子科技大学雷达信号处理国家重点实验室 西安 710071)
针对到达时间差(TDOA)定位中出现的非线性估计问题,该文提出一种线性校正TDOA定位算法。首先将高度非线性的TDOA定位方程组转化为一组关于辐射源位置的伪线性方程,利用加权最小二乘(WLS)估计进行初始求解;然后在此基础上通过一阶泰勒级数展开把伪线性方程组转化为关于估计偏差的线性加权最小二乘问题并进行求解,分析了所提算法在测量误差较小时的有效性。最后提出了一种基于加权最小二乘估计的恒加速度运动辐射源的定位方法,相应的估计性能在测量误差较小时也接近克拉美罗界(CRLB)。计算机仿真结果验证了该算法的有效性。
信号处理;无源定位;到达时间差;加权最小二乘估计;线性校正;恒加速度
1 引言
无源定位技术在跟踪[1]、导航[2]、无线通信和传感器网络[3]等领域有着广泛的应用。就具体的定位参数信息而言,主要包括到达时间(Time Of Arrival, TOA)、到达时间差(Time Difference Of Arrival, TDOA)、到达角(Angle Of Arrival, AOA)和到达频差(Frequency Difference Of Arrival, FDOA)等[4- 6];其中基于多站TDOA信息的定位技术对接收系统的要求较低,具有定位成本低、精度较高[7]等优点,因而受到越来越多的关注。
利用TDOA信息对辐射源进行定位本质上是一个非线性估计问题,可以利用迭代方法求解。目前常见的基于迭代求解的定位算法有泰勒级数法[8]和拟牛顿法[9]等,它们的收敛性依赖于初始值的选取和代价函数的非线性程度。当初始值接近真实值时,算法能快速收敛;但是在代价函数高度非线性并且初始值选择不好的情况下,容易落入到局部极小点,而且收敛性难以保证。基于封闭解的TDOA定位算法有球面相交(Spherical Intersection, SI) 法[10]、两级加权最小二乘(Two-step Weighted Least Squares(WLS))法[11]、近似最大似然估计(Approximate Maximum Likelihood, AML)法[12]和多维尺度分析(MultiDimensional Scaling, MDS) 法[13]等;其中Two-step WLS法在第2级加权最小二乘估计时涉及到开方运算,产生的定位结果具有模糊性 ,并且可能出现虚数解;而SI法和AML法将TDOA定位问题转化为二次多项式求解问题,当两根均为正数或出现虚数解时,根的选取对定位精度有很大影响。MDS法在加权矩阵的求解过程中出现矩阵奇异的情况,加载因子的选取对定位结果影响较大。为此,本文提出了一种线性校正TDOA定位算法,该算法首先利用加权最小二乘估计对伪线性定位方程组进行初始求解;然后将伪线性方程组转化为关于位置估计偏差的线性方程组进行求解;同时,本文分析了算法在测量误差较小时的有效性,并将所提方法应用到恒加速度运动辐射源的定位上。仿真结果表明该算法较传统算法有较好的定位性能。
2 多站TDOA定位模型
假定3维空间中任意分布的M个接收站,第i个接收站的位置坐标为si=[xi, yi, zi]T, i=1, 2,…,M,辐射源位置坐标为u=[x, y, z]T。辐射源u到接收站si的距离为

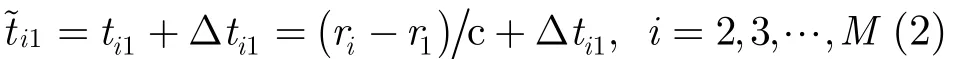
不失一般性,本文选取s1作为参考接收站,不考虑非视距传播的影响,根据TDOA定位原理可得式中~ti1为TDOA测量值,ti1表示信号从辐射源u到接收站si和参考接收站s1之间的真实时间差,c为真空中电磁波传播速度,Δti1为TDOA测量误差。
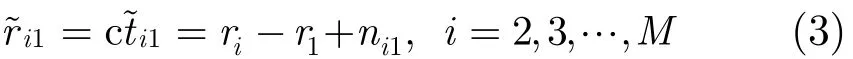
用c同时乘以式(2)两端,可以得到距离差定位方程:式中ni 1=cΔti 1表示相应的距离差测量误差。令fi1(u)=ri-r1,将式(3)写成矢量形式为

3 线性校正TDOA定位算法
3.1 加权最小二乘估计
由式(1)可知,距离差定位模型式(3)是关于辐射源位置u的高度非线性方程,将式(3)右端第2项r1移至左端,两边同时平方得

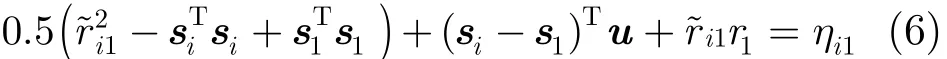
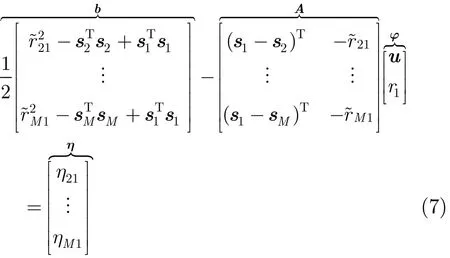
式(7)为关于φ的线性方程,对其进行加权最小二乘求解可得

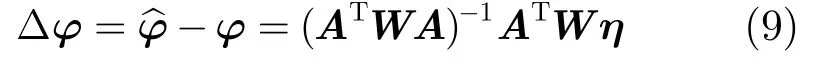
这个过程是在假设u与r1相互独立的前提下进行的,而事实上,它们受限于方程式(1)。
3.2 线性校正TDOA定位算法
由式(8)得到的辐射源位置ˆu只是一种粗估计,本文利用u和r1之间的关系,提出一种线性校正定位方法。考虑到实际值u与估计值ˆu之间存在偏差,不妨设此偏差为Δu,则实际位置矢量为=ˆ-uu
进行一阶泰勒级数展开可得
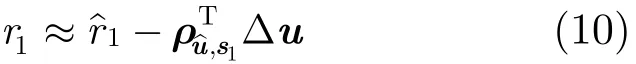


式中
对式(12)进行加权最小二乘求解可得
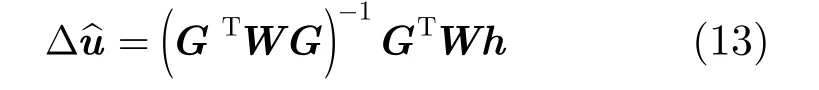
则校正后的辐射源位置为

下面求估计~u的偏差及协方差矩阵。将=Δ hGu +η和分别代入式(13)和式(14)可得
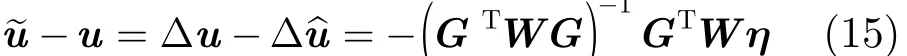
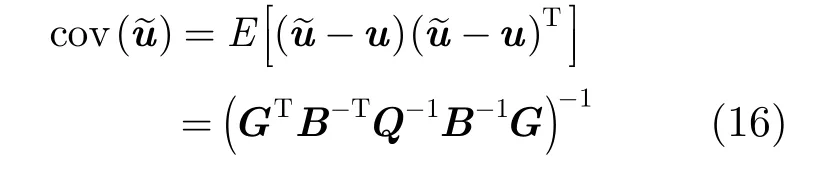
3.3 性能分析
克拉美罗界是所有无偏估计所能达到的下界,由文献[11]可知基于TDOA定位问题的克拉美罗界为

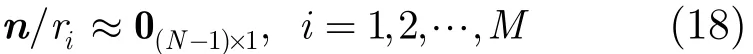
根据G,B的定义可知矩阵-1B G的第i-1行,
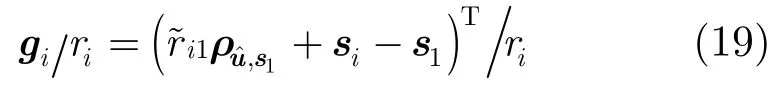
根据式(9)可将Δu表示为测量误差n21,n31,…,nM -1线性组合的形式,由文献[15]可知在条件式(18)下有



3.4 复杂度分析
采用浮点运算次数(floating-point operations, flops)作为算法复杂度的度量,1个flop表示一次加、减、乘、除或开方运算。由文献[16, 17]可知,对n×n维矩阵求逆需要(2n3-2n2+n)flops,对m×n维矩阵进行奇异值分解需要(4m2n+22n2)flops。因此,两级WLS法、MDS法和本文方法的复杂度分别约为9M2+33M+214,8M3+25M2+137和15M2+56M+94。可见,本文方法的复杂度介于两级WLS法和MDS法之间,但从下面的仿真中可以看出本文方法的性能要明显优于这两种方法;而泰勒级数法的复杂度约为(50M+19)l,其中l表示迭代次数,其取值依赖于初始值的选取;一般情况下,与闭式解相比,迭代算法需要更多的运算量。
4 基于多时刻TDOA测量值的运动辐射源定位算法
4.1 运动辐射源参数矢量加权最小二乘估计
常见的目标运动模型有匀速运动模型、匀加速运动模型以及变加速运动模型。其中,匀加速运动是一种典型的运动形式,在水下目标运动分析、SAR成像及目标跟踪等领域[1,18,19]有着重要的应用。基于此,本文提出一种利用加权最小二乘估计的恒加速度运动辐射源的定位方法。不妨设运动辐射源的初始位置、速度及加速度矢量分别为在第tk时刻,辐射源和接收站位置可表示为其中si,0和vi,0分别为第i个接收站的初始位置和速度,ai为加速度矢量。令时间矩阵为,则在t时刻辐射源和第i个接收站的位置k可分别表示为此时辐射源u到第i个接收站si, k的距离为相应的距离差定位方程为其中0,1,,
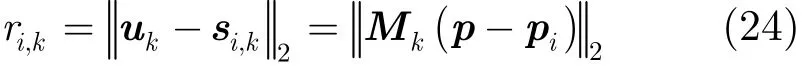

kK =…,1,2,,
iM =… 。将式(25)写成矢量形式可得


式(28)的加权最小二乘估计为

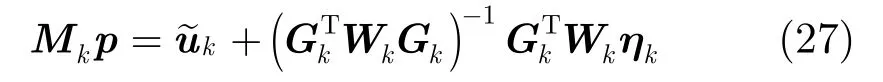
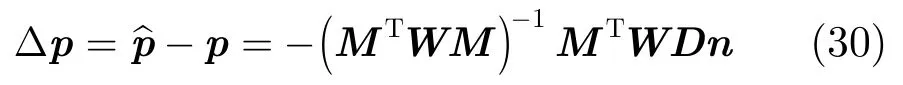
由于测量误差n为零均值,E[Δp]=09× 1,即由式(29)所得估计pˆ在测量误差较小时为无偏估计。由式(30)和W的定义可得估计pˆ的协方差矩阵为

4.2 性能分析
基于多时刻TDOA测量值的运动辐射源定位问题的克拉美罗界为[11]
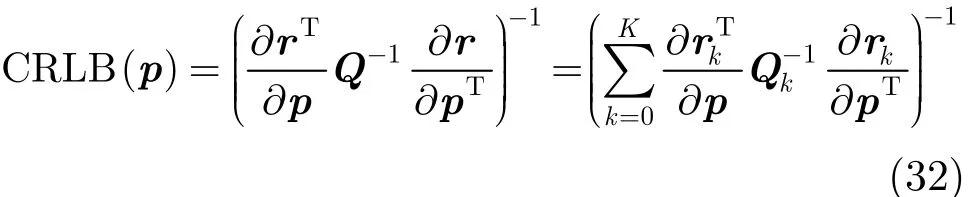



由3.3节中的式(22)及ρa, b的定义可得

将式(35)和式(36)分别代入式(32)和式(34)可知

即由式(29)所得的估计ˆp近似为有效估计。
5 仿真实验
为了检验文中方法对辐射源的定位性能,将该方法与两级WLS法、泰勒级数法、MDS法及克拉美罗界的仿真结果进行比较。采用估计均方根误差和估计偏差对各算法的定位性能进行衡量,其定义式分别为式中为第l次估计的辐射源初始位置、速度或加速度,L=104为蒙特卡罗仿真实验次数。表1 给出了5个接收站的初始位置si,0、速度vi,0及恒加速度ai信息。

表1 接收站初始位置、速度及恒加速度
假设各个时刻TDOA测量值服从均值为零、方差为σ2的高斯分布,则Qk满足对角线元素为c2σ2,非对角线元素为0.5c2σ2[11]。首先利用k=0时刻的TDOA测量值对辐射源初始位置u0进行估计。为了对比公平,用式(8)所得初始估计计算两级WLS法和MDS法的权值及作为泰勒级数法的迭代初值。
仿真1 近场辐射源初始位置坐标为u0=[285, 325,275]T,噪声功率c2σ2从10-1变化到102.5。图1(a),图1(b)分别为各算法随噪声功率变化时的辐射源位置估计偏差和均方根误差的统计结果。从图1(a),图1(b)可以看出,在噪声功率较小时,各算法对辐射源位置的估计偏差均接近零,这说明了文中方法在噪声功率较小时近似为无偏估计;另外,文中方法和两级WLS法、泰勒级数法及MDS法的均方根误差均接近克拉美罗界。随着测量误差的增加,各算法的估计偏差和均方根误差都会有所增加,其中两级WLS法最先偏离克拉美罗界,泰勒级数法的估计偏差和均方根误差均出现急剧增加的现象;而文中方法的估计偏差和均方根误差一直保持最小,具有较好的定位性能。
仿真2 远场辐射源的初始位置坐标为u0= [3000,2500,2000]T,噪声功率c2σ2从10-4变化到100。图2(a),图2(b)分别给出了各算法对远场辐射源位置估计随噪声功率变化的估计偏差和均方根误差的统计结果。从图2(a),图2(b)可以得出与仿真1中类似的结论,在噪声功率较小时,各算法对远场辐射源位置的估计偏差均较小,近似为无偏估计;几种方法的均方根误差都能够很好的达到克拉美罗界。随着噪声功率的增加,各算法的估计偏差和均方根误差均有所增加,而文中方法的估计偏差和均方根误差一直保持最小。

图1 各算法对近场辐射源位置的定位性能示意图
接下来利用多个时刻TDOA测量值对运动辐射源参数矢量进行估计。
仿真3 设运动辐射源的初始位置、速度及加速度分别为u0=[600,650,550]T, v0=[-200,150, 400]T,a=[30,20,-20]T。将式(29)所得结果作为泰勒级数法的迭代初始值,噪声功率c2σ2从10-2变化到100.8,图3(a),图3(b)和图3(c)分别给出了文中方法与泰勒级数法对运动辐射源参数矢量估计随噪声功率变化的均方根误差的统计结果。可以看出,K=5时的克拉美罗界要明显低于K=2时,这是因为在K=5时具有更多能利用的TDOA测量信息。文中方法与泰勒级数法在噪声功率较小时均接近克拉美罗界,这也验证了4.2节中关于所得辐射源参数矢量估计的协方差矩阵近似等于克拉美罗界的结论。随着噪声功率的增加,泰勒级数法的均方根误差在两种情况下均出现急剧增加的现象;而文中方法的均方根误差一直接近克拉美罗界,具有较好的定位性能。

图3 本文方法与泰勒级数法对运动辐射源的定位性能示意图
MDS法在求解过程中采用奇异值分解技术,并将最小奇异值作为对角加载因子,一方面会增加运算量,另一方面加载量的大小会对定位精度产生影响[6]。两级WLS法在第2步求解过程中利用u与r1之间的关系对初始估计uˆ进行优化,同时忽略了Δu和Δr1的高阶项,并且由于涉及到开方运算,会产生模糊解,甚至产生复数解;而本文方法对伪线性方程组进行线性化,进而求取偏差Δuˆ对估计uˆ进行校正。线性化过程中只忽略了Δu的高阶项,不涉及开方运算,因此不会产生模糊解及复数解,这也是本文方法性能优于两级WLS法的主要原因。从仿真实验也可以看出,本文方法要明显优于两级WLS法。由于TDOA定位问题高度非线性,泰勒级数法很容易出现发散或者局部收敛的现象,这在仿真实验中也得到了验证。
6 结束语
针对传统TDOA定位中出现的非线性参数估计问题,提出了一种线性校正TDOA定位算法。通过引入中间变量将高度非线性定位方程转化为关于辐射源位置的伪线性方程,并进行加权最小二乘求解;然后在此基础上把伪线性方程组转化为关于辐射源位置估计偏差的线性方程进行求解并对初始估计进行线性校正。本文分析了文中方法在测量误差较小时对辐射源位置的估计近似为有效估计。最后,提出了一种基于加权最小二乘估计的恒加速度运动辐射源的定位算法。实验结果表明所提方法具有较好的定位性能。
联合多种量测值进行定位能够提高定位精度,目前的联合定位场景如TDOA/FDOA及TDOA/ AOA等场景[3,6]受到广泛关注,本文方法的线性校正思想同样可以应用到这些定位场景。下一步将以本文结论为基础,针对接收站位置存在误差的情况,深入研究适用于接收站位置误差情况下的稳健定位方法。
[1] Dogancay K and Sakhtsari A H. Target tracking by time difference of arrival using recursive smoothing[J]. Signal Processing, 2005, 85(4): 667-679.
[2] Zhang H Q and Zhang Y G. A robust algorithm for multiple disjoint moving sources localization with erroneous sensor locations[J]. Journal of Communications, 2013, 8(6): 345-350.
[3] Gholami M R, Gezici S, and Strom E G. Improved position estimation using hybrid TW-TOA and TDOA in cooperative networks[J]. IEEE Transactions on Signal Processing, 2012, 60(7): 3770-3785.
[4] Huang J, Xue Y B, and Yang L. An efficient closed-form solution for joint synchronization and localization using TOA[J]. Future Generation Computer Systems, 2013, 29(3): 776-781.
[5] Chan Y T, So H C, Lee B H, et al.. Angle of arrival localization of an emitter from air platforms[C]. Proceedings of the 26th Annual IEEE Canadian Conference of Electrical and Computer Engineering, Regina, Canada, 2013: 1-5.
[6] Wang G, Li Y M, and Ansari N. A semidefinite relaxation method for source localization using TDOA and FDOA measurements[J]. IEEE Transactions on Vehicular Technology, 2013, 62(2): 853-862.
[7] 李万春, 魏平, 肖先赐. 一种新的稳健的TDOA定位算法[J].电子与信息学报, 2006, 28(11): 2019-2021.
[8] Fard H T, Atashbar M, Norouzi Y, et al.. Multireference TDOA-based source localization[J]. Turkish Journal of Electrical Engineer & Computer Sciences, 2013, 21(11): 1920-1929.
[9] Hao B and Li Z. BFGS quasi-Newton location algorithm using TDOAs and GROAs[J]. Journal of Systems Engineering and Electronics, 2013, 24(3): 341-348.
[10] Smith J O and Abel J S. Closed-form least-squares source location estimation from range-difference measurements [J]. IEEE Transactions on Acoustics, Speech, and Signal Processing, 1987, 35(12): 1661-1669.
[11] Y Chan T and Ho K C. A simple and efficient estimator for hyperbolic location[J]. IEEE Transactions on Signal Processing, 1994, 42(8): 1905-1915.
[12] Chan Y T, Hang H Y C, and Ching P C. Exact and approximate maximum likelihood localization algorithms[J]. IEEE Transactions on Vehicular Technology, 2006, 55(1): 10-16.
[13] Wei H W, Peng R, Wan Q, et al.. Multidimensional scaling analysis for passive moving target localization with TDOA and FDOA measurements[J]. IEEE Transactions on Signal Processing, 2010, 58(3): 1677-1688.
[14] 段凯宇, 张力军. 基于到达角Kalman滤波的TDOA/AOA定位算法[J]. 电子与信息学报, 2006, 28(9): 1710-1713.
[15] Yang L and Ho K C. An approximately efficient TDOA localization algorithm in closed-form for locating multiple disjoint sources with erroneous sensor positions[J]. IEEE Transactions on Signal Processing, 2009, 57(12): 4598-4615. [16] Chan F K W, So H C, and Ma W K. A novel subspace approach for cooperative localization in wireless sensor networks using range measurements[J]. IEEE Transactions on Signal Processing, 2009, 57(1): 260-269.
[17] Meyer C D. Matrix analysis and applied linear algebra [M]. Philadelphia: Siam, 2000: 119-120.
[18] Zhang Y J and Xu G Z. Bearings-only target motion analysis via instrumental variable estimation[J]. IEEE Transactions on Signal Processing, 2010, 58(11): 5523-5533.
[19] 孙兵, 周荫清, 陈杰, 等. 基于恒加速度模型的斜视SAR成像CA-ECS算法[J]. 电子学报, 2006, 34(9): 1595-1599.
朱国辉: 男,1987年生,博士生,研究方向为无源定位技术.
冯大政: 男,1959年生,教授,博士生导师,研究方向为盲信号处理、雷达信号处理、无源定位和阵列信号处理等.
周 延: 男,1987年生,博士生,研究方向为空时自适应信号处理.
A Linear-correction Based on Time Difference of Arrival Localization Algorithm
Zhu Guo-hui Feng Da-zheng Zhou Yan Zhao Hai-xia
(National Key Laboratory of Radar Signal Processing, Xidian University, Xi’an 710071, China)
A novel Time Differences Of Arrival (TDOA) localization algorithm based on linear-correction is proposed to address the nonlinear problem of TDOA positioning. Firstly, the proposed algorithm reformulates the highly nonlinear TDOA equations into a set of pseudo-linear ones and the Weighted Least Squares (WLS) estimator is used to obtain the initial emitter position estimation. Then a linear weighted least squares problem with respect to the estimation bias is formulated through utilizing first-order Taylor-series expansion to the pseudo-linear equations. The effectiveness of the proposed method is theoretically analyzed under small noise postulation. Finally, the extension to the general case of moving emitter with constant acceleration localization scenario is also presented and the corresponding estimation accuracy can achieve the Cramer-Rao Lower Bound (CRLB) as well. Computer simulation results demonstrate the effectiveness of the proposed algorithm.
Signal processing; Pssive location; Time Difference Of Arrival (TDOA); Weighted Least Squares (WLS) estimates; Linear-correction; Constant acceleration
TN971
A
1009-5896(2015)01-0085-06
10.11999/JEIT140313
2014-03-10收到,2014-06-13改回
国家自然科学基金(61271293)资助课题
*通信作者:朱国辉 zhugh@stu.xidian.edu.cn

