圆锥曲线最值问题常用解题方法及策略
新疆兵团第一师高级中学 李志刚
针对近年来的高考试题来看,教学中“圆锥曲线的最值问题”的命制借助《课程标准》与《考试大纲》的要求,圆锥曲线的最值问题是各种考试的常见题型,解析此类问题和解代数中的最值问题方法类似。但是圆锥曲线的最值问题与曲线有关,教学中可以根据学情不同,进行归纳和整理出:利用曲线的性质研究圆锥曲线的最值问题是它特有的方法。
一、化为二次函数,求二次函数的最值
依据条件求出用一个参数表示的二次函数解析式而自变量都有一定的变化范围,然后用配方法求出限制条件下函数的最值,就可得到问题的解。

例1曲边梯形由曲线及直所围成,试问通过曲线上的哪一点作切线,能使此切线从曲边梯形上切出一个最大面积的普通梯形。
[分析] 先求出适合条件的一条切线方程,再求出这条切线与直线的交点坐标,根据梯形面积公式列出函数关系式,再求出最值。
[解] 设为曲线上一点,过这点的切线的斜率是,故切线方程是
切线①与x=1的交点的纵坐标是,与x=2的交点的纵坐标是,所以切线①在曲线梯形上切出梯形的中位线长,梯形的高为1.故普通梯形的面积为
当时, 最大,故过点作切线能切出最大面积的普通梯形。
二、利用圆锥曲线性质求最值
有些问题先利用圆锥曲线的定义或性质给出关系式,再利用几何或代数方法求最值,可使题目中的数量关系更直观,解题方法更简捷。

例2 已 知 双 曲 线的右焦点为F,点A(9,2),试在双曲线上求一点M,使M的值最小,并求这个最小值。
[解]如图,作右准线l,作MN⊥l于N,作 AA´⊥A´于A´,由题意得。由双曲线的第二定义有
所以当且仅当AA´与双曲线右支的交点,即点M为时,取最小值。的最小值为。
三、化为一元二次方程,利用判别式求最值
把圆锥曲线的最值问题转化为含有一个未知量的一元二次方程,利用△≧0解得要求未知量的范围,然后确定其最值。
例3 直线l:y=x+9,椭圆C:,求以椭圆C的焦点F1,F2为焦点,且与直线有l公共点M的椭圆长轴最短的椭圆方程。
[分析]由于直线l与所求椭圆有公共点,可以由方程组得到一个一元二次方程,再利用判别式确定所求椭圆长轴的最小值。
[解]椭圆C的焦点设所求椭圆C´的方程为

椭圆的长轴最短时,a2=45
此时 x=-5,y=4,点M的坐标为(-5,4)
四、利用不等式求最值
列出最值满足的关系式,利用均值不等式中等号成立的条件求最值。
例4 定长为3的线段AB的两个端点在抛物线y2=x上移动,是线段M的AB中点,求M到y轴的最短距离。
[分析]设
故所求椭圆方程为,则,即求x的最小值。
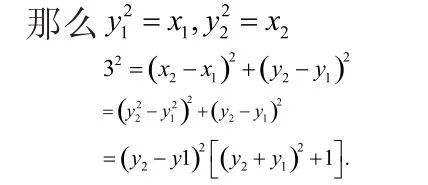
线段 AB的中点M(x,y)到y轴的距离为

当且仅当时,x取得最小值,此时,故M点到y轴的最短距离是
五、利用函数的性质求最值
有些圆锥曲线的最值问题可以先转化成为函数问题,然后利用函数的单调性、有界性等性质求最值。

例5 已 知 椭 圆与x轴、y轴的正半轴分别相交于点AB,当点p在第一象限内并在椭圆上变动时,求四边形OAPB的面积S的最大值。

六、利用平面几何的有关知识求最值
对于有些圆锥曲线求最值问题,可以将其转化为平面几何问题,借助一些平面几何知识求最值。
例6 已知椭圆,点A(4,0)是它的右焦点,B(2,2) 是椭圆内一点,M是椭圆上一动点,求|MA|+|MB|的最大值和最小值。

[分析]左焦点A´(-4,0),由椭圆定义知|MA|+|MA´|=10 ,而|MB|·|MA´|·|A´B´|在同一三角形中,利用三角形三边之间的关系式求最值。
[解]椭圆左焦点A´(-4,0),由椭圆定义可得|MA|+|MA´|=10。
如图:

当点M在BA´的延长线上时,|MA|+|MB|有最大值,即

如图,

即当点M在A´B的延长线上时,|MA|+|MB|有最小值,即

通过试题的讲解与分析,引导学生从不同的角度来加以认知和掌握圆锥曲线。针对圆锥曲线的最值问题从方程与曲线着手,也反映了数学问题中的数与形的密切关系,这类问题涉及的数学知识较多,解题方法灵活。
因此,求圆锥曲线最值问题能进一步的促进数学知识的有机联系和融会贯通,也能不断地使学生的数学阶梯技能得到全面训练与提升。

