考虑土体材料二维空间变异特性的边坡可靠度分析

褚雪松,李 亮,吕 惠

(青岛理工大学土木工程学院,山东青岛 266033)

考虑土体材料二维空间变异特性的边坡可靠度分析

褚雪松,李 亮,吕 惠

(青岛理工大学土木工程学院,山东青岛 266033)

为了更合理地分析边坡的可靠性,提出了考虑土体二维空间变异特性的边坡可靠度分析方法,将边坡区域离散为系列单元,假设单元内土体材料参数完全相关,通过假定的自相关函数确定单元之间土体材料参数的相关系数,采用子集模拟法抽样,运用和声搜索算法搜索最小的安全系数作为该次抽样的结果。将提出的可靠度分析方法应用于两个边坡实例的可靠度分析中,并与已有结果进行对比分析,结果表明,考虑土体材料参数的空间变异特性后,边坡的破坏概率降低,边坡可能的破坏区域逐渐增多。

边坡稳定;空间变异特性;可靠度分析;子集模拟方法;极限平衡法;破坏概率

基于极限平衡的确定性分析方法仍然是当前边坡稳定分析的主要手段之一,但是越来越多的研究表明,可靠度分析方法考虑了土体材料的变异特性,可以作为确定性分析方法的有益补充[1-2]。导致土体材料参数变异特性的原因有很多,比如土体材料本身的空间变异、试验方法、数学模型等[3],本文仅考虑土体材料本身固有的空间变异特性对边坡可靠度的影响。龚勋等[4]采用二维随机场与蒙特卡罗方法相结合,将土体的黏聚力作为一个空间二维随机场研究了土体空间变异特性对浅基础极限承载能力的影响;李典庆等[5]利用随机响应面法进行了边坡可靠度分析;以上方法均是在有限元方法的框架之内完成的,国外Griffiths等[6-8]也在有限元方法的框架之内开展了一系列有意义的工作。而极限平衡方法仍然是相对较简单且易于工程应用的方法之一,因此有必要在极限平衡框架之内,提出考虑空间变异特性的边坡可靠度分析方法。虽然JI等[9]在极限平衡方法的框架之内,提出了基于Excel的边坡可靠度分析方法,然而其模拟土体材料二维空间变异特性的手段较为复杂,本文提出一种基于单元的二维空间变异特性模拟方法(图1),并与文献[9]的结果进行对比。

图1 二维空间变异特性模拟示意图

1 土体材料空间变异特性

将图1所示边坡区域离散为20个单元,每个单元中土体材料的参数比如密度ρ、黏聚力c、内摩擦角φ等都是完全相关的,不同单元之间土体材料参数是相关的,相关系数可由自相关函数确定,本文采用经典负指数自相关函数来确定[10]:

式中:ρi,j为单元i、j中参数的相关系数;xi、yi分别为第i个单元形心的x、y坐标;xj、yj分别为第j个单元形心的x、y坐标;λx、λy分别为x、y方向上土体材料的自相似距离,Degroot等[11]研究表明,λy在0.5～3.0之间,λx在15～30之间。由公式(1)可知,在自相似距离一定的前提下,两个单元之间的距离越大,单元土体材料参数之间的相关系数越小。当λx→+∞、λy→+∞时,所有单元土体材料参数之间的相关系数均为1,图1所示边坡即成为所谓的均质边坡。

如上所述,空间变异特性实际上是通过考虑不同单元材料之间的相关系数来实现的,可根据划分的单元和公式(1)计算相关系数。以图1所示的边坡为例,假设只考虑每个单元内土体材料的c、φ作为随机变量,则共有40个随机变量,需要构造一个40×40的相关系数矩阵,图2为相关系数矩阵示意图。本文基于单元的二维空间变异特性的模拟实际上是随机场均化的一种特例,单元的尺寸可以控制在其相应2倍的自相似距离以内[12]。图2中ρc-φ是c与φ之间的相关系数,其一般是负相关的[1],图2示意图中假设所有单元的c与φ之间相关系数均相等,当然也可以根据实际情况,指定不同的相关系数,在此不再赘述。

2 基于子集模拟法的边坡可靠度分析

子集模拟法是一种适用于研究小概率事件的高效随机模拟方法,其基本思路是用若干中间失效事件表达小概率的失效事件,小概率失效事件的概率值可以表示为相应中间失效事件概率值的乘积[13-16]。通过这种方式,将小概率事件模拟问题转化为一系列发生概率较大的中间失效事件的模拟问题。在模拟过程中,通过马尔科夫链原理进行条件样本抽样,使样本空间逐步逼近小概率事件发生的失效区域,具体说来,在根据当前样本产生备选样本时,采用文献[13]提出的用建议分布函数产生备选样本点,下面在极限平衡方法框架内对子集模拟法的步骤进行描述。

2.1 基于极限平衡法的功能函数

子集模拟法是在蒙特卡罗法的基础上发展而来的。蒙特卡罗法中最基本的方法就是抽样,即产生符合土体参数分布的一系列值,土体参数一般假定服从正态或者对数正态分布,后基于这一系列土体参数值进行确定性分析[1]。本文基于圆弧滑动面假定,利用简化毕省普法[17]计算滑动面的安全系数,采用和声搜索算法[18-20]搜索最小的安全系数及其对应的滑动面作为某次抽样的结果。在可靠度分析中边坡失稳与否是通过判断功能函数值是否小于零来实现的,若某次抽样的结果小于零,则认为边坡失稳,所以本文的功能函数G定义为

式中:X为土体参数向量;Fsmin(X)为相应于X的边坡最小安全系数;m为随机变量个数。

2.2 子集模拟法步骤

a.利用常规蒙特卡罗法产生一系列抽样值Xi=(xi1,xi2,…,xim)(i=1,2,…,N),N为抽样个数,计数器J=0。

b.对于某一抽样值Xi进行确定性分析,利用和声搜索算法找出最小的安全系数Fsi(i=1,2,…,N)。

c.将Fsi按升序排列,同时更新Xi。

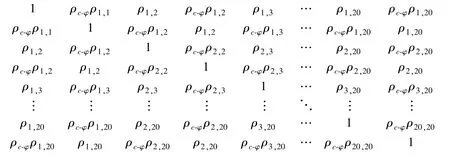
图2 相关系数矩阵

e.将前Nc个抽样值作为初始值,分别产生1/p0个条件抽样值,以第j个初始抽样值Xj为例,其相应的独立标准正态分布空间内的值为ξj1,ξj2,…, ξjm,由公式(3)计算其上、下限:

式中:uk、lk分别为第k个参数的上、下限;ηk为N个抽样值的标准差;xu为N个抽样值的均值;w为常量,一般取2.0[12]。

a.根据式(3)所求上、下限,随机生成ξ＇jk。

e.对前Nc个抽样值中的每一个均执行步骤a、b、c、d,如此共产生N个新的条件抽样值,即目前N个抽样结果均小于fs,J。

综上可知,子集模拟法共需要N、w、p0这3个参数,根据文献[12]研究的结果,本文算例分析中取N=500,w=2.0,p0=0.1。子集模拟法得到的pf即是边坡的破坏概率。

3 算例分析

对文献[9]中分析的两个算例利用本文可靠度分析方法(以下简称本文方法)重新进行计算,并将结果与文献[9]结果进行对比分析。

3.1 算例1

图3为修建在软土地基上的边坡,其中上部土层的参数作为定值,ρ=1 900 kg/m3,c=5 kPa,φ= 30°。下部软土层的不排水强度cu作为正态分布随机变量,其均值为25 kPa,变异系数Cov=0.25,即cu的标准差为6.25 kPa。软土层的密度视为定值,且与上部土层密度相等。文献[11]研究表明,λy在0.5～3.0之间,λx在15～30之间,所以在划分单元时,宽度间距要小于土层参数的λx,高度间距要小于λy,由于文献[9]假定λx=20m,λy=2m,本文将下部软土层划分为12个单元,宽度间距10m,高度间距2m。

图3 软土地基上的边坡离散示意图

首先利用自编的Fortran程序进行确定性分析,即将下部软土层的cu取为均值,利用简化毕肖普法计算给定滑动面的安全系数,采用和声搜索算法找出最小安全系数及其对应的滑动面(确定性临界滑动面);其次不考虑软土层的空间变异特性,即12个单元之间的cu是完全相关的,进行了边坡破坏概率的求解,最后根据文献[9]给出的自相似距离,进行4种不同参数组合下的计算。

3.1.1 确定性分析

图4为确定性分析得到的确定性临界滑动面,其对应的简化毕肖普安全系数为1.476,文献[9]给出了Spencer法的结果为1.462,将本文的确定性临界滑动面用Spencer法重新进行了计算,其安全系数为1.466,这与文献[9]的1.462基本一致,证明本文自编的Fortran程序是正确的。

图4 确定性临界滑动面(算例1)

3.1.2 完全相关的破坏概率

当下部软土层的cu在空间上完全相关时,利用本文的可靠度分析方法进行边坡破坏概率的计算,得到pf=9.08%。对于子集模拟法的每次抽样,均须利用和声算法搜索出对应的最小安全系数及其对应的滑动面,图5为计算过程中每次抽样的最小安全系数对应的滑动面集合(即破坏概率对应的滑动面集合),由此可以看出,边坡最可能的破坏区域(下同)。由图5可见,不考虑cu空间变异特性时,边坡主要有两个破坏模式,这为边坡的设计与治理提供了决策依据。

图5 破坏概率对应的滑动面集合(算例1)

3.1.3 几种参数组合的破坏概率

表1为文献[9]考虑的4种参数组合,利用本文方法重新进行了计算,同时与文献[9]的计算结果进行对比,两种方法所得规律基本一致,破坏概率pf在同一数量级,具体的差别有可能是不同的条块数以及不同的搜索算法导致,综合来看,文献[9]计算方法可能没有找到某一抽样的最小安全系数,导致破坏概率偏小。

表1 破坏概率计算结果对比(算例1)

图6为破坏概率对应的滑动面集合比较。由图6(a)可见,λx=λy=1000m时,所得图形与图5基本一致,即自相似距离趋于+∞时,相当于不考虑土层参数之间的空间变异性,即完全相关。由图6(b)知,当λy=2m时,边坡最可能的破坏区域增加为4个,这说明考虑土层参数的空间变异性以后,虽然边坡可能的破坏区域增加,但最终破坏概率降低,这与文献[9]的结论一致。

图6 破坏概率对应的滑动面集合比较(算例1)

3.2 算例2

图7为c-φ边坡离散示意图,其中密度在计算中视为定值(1900 kg/m3),分别将c＇、φ＇作为正态分布随机变量考虑,其均值以及变异系数Cov分别为15 kPa、0.3以及23°、0.1,即c＇和φ＇的标准差分别为4.5 kPa和2.3°。将边坡区域划分为28个单元,宽度间距5m,高度间距2m,其示意图如图7所示。c＇、φ＇之间的相关系数为-0.5。

图7 c-φ边坡离散示意图

图8 确定性临界滑动面(算例2)

3.2.2 完全相关的破坏概率

当仅考虑c＇、φ＇之间的相关系数,不考虑c＇与φ＇在空间上的变异特性时,应用本文方法进行边坡可靠度分析,得到的破坏概率为9.28%,图9为破坏概率对应的滑动面集合。

图9 破坏概率对应的滑动面集合(算例2)

3.2.1 确定性分析

图8为确定性分析得到的确定性临界滑动面,其对应的简化毕肖普安全系数为1.213,文献[9]给出了Spencer法的结果为1.226,将本文的确定性临界滑动面用Spencer法重新进行计算,其安全系数为1.223,这与文献[9]的1.226基本一致。

3.2.3 几种参数组合的破坏概率

表2为文献[9]的4种参数组合,利用本文方法进行了计算,同时与文[9]结果进行对比,两种方法所得规律基本一致,破坏概率pf在同一数量级。破坏概率对应的滑动面集合如图10所示,可以得到与算例1相同的规律,不再赘述。

表2 破坏概率计算结果对比(算例2)

图10 破坏概率对应的滑动面集合比较(算例2)

4 结 论

a.考虑土体材料参数的空间变异特性后,边坡的破坏概率降低,即不考虑土体材料参数的空间变异特性时,所得破坏概率偏大。

b.由最小安全系数对应的滑动面集合来看,考虑土体材料参数空间变异特性以后,边坡可能的破坏区域逐渐增多。

c.基于划分单元的空间变异特性可靠度分析方法可以尝试应用于边坡可靠度分析。

[1]陈祖煜.土质土坡稳定分析:原理·方法·程序[M].北京:中国水利水电出版社,2003:372-373.

[2]DUNCAN J M.Factors of safety and reliability in geotechnical engineering[J].Journal of Geotechnical and Geoenvironmental Engineering,2000,126(4):307-316.

[3]WHITMAN R V.Organizing and evaluating uncertainty in geotechnical engineering[J].Journal of Geotechnical and Geoenvironmental Engineering,2000,126(7):583-593.

[4]龚勋,张冬梅,黄宏伟.二维空间随机场的浅基础极限承载力可靠度分析[J].地下空间与工程学报,2012 (增刊2):1676-1679.(GONG Xun,ZHANG Dongmei, HUANG Hongwei.Reliability anlysis of allowable pressure on shallow foundation based on 2D random field[J]. Chinese Journal of Underground Space and Engineering, 2012(Sup 2):1676-1679.(in Chinese))

[5]李典庆,周创兵,陈益峰,等.边坡可靠度分析的随机响应面法及程序实现[J].岩石力学与工程学报,2010,29 (8):1513-1523.(LI Dianqing,ZHOU Chuangbing, CHEN Yifeng,et al.Reliability analysis of slope using stochastic response surface method and code implementation[J].Chinese Journal of Rock Mechanics and Engineering,2010,29(8):1513-1523.(in Chinese))

[6]GRIFFITHS,D V,FENTON,G A.Probabilistic slope stability analysis by finite elements[J].Journal of Geotechnical and Geoenvironmental Engineering,2004, 130(5):507-518.

[7]GRIFFITHS D V,HUANG J,FENTON GA.Influence of spatial variability on slope reliability using 2-D random fields[J].Journal of Geotechnical and Geoenvironmental Engineering,2009,135(10):1367-1378.

[8]GRIFFITHSD V,HUANG J,FENTON G A.Probabilistic infinite slope analysis[J].Computers and Geotechnics, 2011,38(4):577-584.

[9]JI J,LOW B K.Modeling 2-D spatial variation in slope reliability analysis using interpolated autocorrelations[J]. Computers and Geotechnics,2012,40(3):135-146.

[10]LI K S,LUMB P.Probabilistic design of slopes[J]. Canadian Geotechnical Journal,1987,24(4):520-535.

[11]DEGROOT DJ.Analyzing spatial variability of in situ soil properties[J].Geotechnical Special Publication,1996,58 (1):210-238.

[12]VANMARCKE E H.Probabilisticmodeling of soil profiles [J].Journal of the Geotechnical Engineering Division, 1977,103(11):1227-1246.

[13]AU S K,BECK J L.Estimation of small failure probabilities in high dimensions by subsetsimulation[J]. Probabilistic Engineering Mechanics,2001,16(4):263-277.

[14]AU SK,BECK J L.Subset simulation and its application to seismic risk based on dynamic analysis[J].Journal of Engineering Mechanics,2003,129(8):901-917.

[15]AU S K,CAO Z J,WANG Y.Implementing advanced monte carlo simulation under spreadsheet environment [J].Structural Safety,2010,32(5):281-292.

[16]宋述芳,吕震宙.基于马尔可夫蒙特卡罗子集模拟的可靠性灵敏度分析方法[J].机械工程学报,2009,45 (4):33-38.(SONG Shufang,LV Zhenzhou.Structural reliability sensitivity ananlysis method based on Markov Chain Monte Carlo Subset simulation[J].Journal of Mechnical Engineering,2009,45(4):33-38.(in Chinese))

[17]BISHOP A W.The use of the slip circle in the stability analysis of slopes[J].Geotechnique,1955,5(1):7-10.

[18]GEEM Z W,KIM J H,LOGANATHAN G V.A new heuristic optimization algorithm:harmony search[J]. Simulation,2001,76(2):60-68.

[19]李亮,褚雪松.边坡临界滑动面与临界可靠度滑动面对比分析[J]华中科技大学学报:自然科学版,2012,40 (9):81-85.(LI Liang,CHU Xuesong.Comparative analysis between critical slip surface and critical reliability slip surface of slopes[J].Journal of Huazhong University of Science and Technology:Natural Science Edition,2012, 40(9):81-85.(in Chinese))

[20]李亮,褚雪松,郑榕明.Rosenblueth法在边坡可靠度分析中的应用[J].水利水电科技进展,2012,32(3):53-56.(LI Liang,CHU Xuesong,CHENG Yungming. Application of Rosenblueth method in reliability analysis of soil slopes[J].Advances in Science and Technology of Water Resources,2012,32(3):53-56.(in Chinese))

Reliability analysis of slope stability considering two-dimensional spatial variability of soil

CHU Xuesong,LI Liang,L‥U Hui(School of Civil Engineering,Qingdao Technological University,Qingdao 266033,China)

A method for slope system reliability analysis considering spatial variability of soil is developed to rationally evaluate the reliability of slope stability.The basic idea is that the slope domain is discretized into a series of“elements”, within each of which the soil property is fully correlated.The correlation coefficient among soil properties from different elements is obtained assuming autocorrelation function.Sets of random samples are generated by subset simulation,and harmony search algorithm is adopted to search the minimum factor of safety as the corresponding output.The method is applied to two examples to analyze the reliability and then compare it with existing results.Overall,the results show that the failure probability is lower than the case without considering the spatial variability and the potential failuremodes are greater than thatwithout taking into account the spatial variability.

slope stability;spatial variability;reliability analysis;subset simulation method;limit equilibrium method; failure probability

TU441

A

1006-7647(2015)02-0032-05

10.3880/j.issn.1006 7647.2015.02.007

2013-11-05 编辑:周红梅)

国家自然科学基金(51274126,51008167);大连理工大学海岸与近海工程国家重点实验室开放基金(LP1214)

褚雪松(1977—),女,辽宁铁岭人,副教授,博士研究生,主要从事岩土防灾减灾研究。Email:celldl@126.com