施工缝数值模型及验证

于 婧,刘小军

(西安建筑科技大学土木工程学院,陕西西安 710055)

施工缝数值模型及验证

于 婧,刘小军

(西安建筑科技大学土木工程学院,陕西西安 710055)

为了解决施工缝在钢筋混凝土结构数值计算中的模拟问题,根据已有研究成果,结合施工缝的形成及受力特点,选用合适的模型进行模拟。该模型运用纤维模型的相关研究成果,并综合考虑了施工缝周围区域的平均剪切效应,同时考虑法向拉压性能和切向剪切性能。借助OpenSees软件平台,提出施工缝模型的建模流程,并对4根带缝柱以及两榀RC平面框架的拟静力试验进行了数值模拟。最大荷载和力位移滞回曲线的试验与计算结果表明,该模型可以模拟沿施工缝面的剪切滑动和施工缝面开裂以后钢筋产生较大的滑移所造成的捏缩现象,应用该模型计算的结果与试验结果吻合较好,验证了施工缝模型的合理性和有效性。

施工缝;接缝单元;钢筋混凝土结构;OpenSees软件;数值模型;模型验证

对施工缝基本力学性能研究结果[1-5]表明,作为混凝土浇筑不连续部位,施工缝处的抗拉和抗剪性能均低于整浇混凝土,而且在复合应力和循环荷载下,强度和刚度退化会加剧,因此一旦在实际地震中出现较大的竖向和水平地震分量,施工缝有可能处于拉剪复合受力的状态,造成提前破坏。

施工缝的受力特点明显异于整浇混凝土,且在特定情况下有可能成为结构或构件的薄弱部位,在对现浇钢筋混凝土结构进行数值计算时应能准确体现这一点,但目前的此类计算中,一般均忽略施工缝的影响,按整浇结构进行分析,其中一个重要的原因是没有合适的施工缝模型。

由于接缝面复杂的应力关系和对接触问题的描述存在困难,有关接缝模型方面的研究较少。张卫东等[6]对两榀在不同部位设置施工缝的两层两跨框架采用ANSYS软件进行了计算分析,并采用Combin39弹簧单元模拟施工缝,结果表明施工缝的位置对结构的抗震性能影响是比较明显的;文中仅提到采用Combin39弹簧单元来模拟施工缝,但是对于为何使用该单元模拟施工缝、参数如何取值以及是否经过验证均没有给出说明。

值得借鉴的是有些学者针对土和结构的接触面进行了一些试验研究,并提出一些简化的接触面剪切模型。李通林等[7]研究了不同类型的岩体结构面在剪切过程中应力传递的过程和特点,对剪切过程中结构面的接触及破坏状态作了详细的描述。段云岭等[8]针对水利土木大型混凝土结构中新旧混凝土及岩体与混凝土的交界面,提出了一种材料非线性的接缝数值模型。孙吉主等[9]基于边界面的概念建立了适用于动力问题分析的接触面的边界面塑性模型,以描述接触面剪切应力与剪应变的滞回特性。

另外,应用较广泛的此类接触面模型还有Clough等[10]提出的子-ωs双曲线模型、Brandt[11]提出的简化子-ωs模型、Desai等[12-13]提出的循环荷载作用下接触面非线性弹性模型(并首次将损伤力学的基本理论应用于接触面本构关系)、Boulon等[14]提出的接触面弹塑性模型等,这些模型有一个共同的特点,就是剪切变形都是依据直剪试验的子-ωs关系曲线。

施工缝由接缝面和穿过缝面钢筋两种不同的材料组成,并且各自在法向和切向承担不同的力传递功能,这与上述研究的界面存在很大不同,因此无法用上述界面模型来模拟施工缝,必须建立能描述施工缝独特传力机制的数值模型。本文结合施工缝的形成特点和受力特点,选用文献[15]建立的施工缝模型,借助OpenSees软件平台,提出了施工缝模型的建模流程;并在此基础上,完成对4根带缝柱拟静力试验以及两榀RC平面框架试验的数值模拟,通过数值计算与试验结果的对比,验证施工缝模型的合理性和有效性。

1 施工缝模型简介

建立施工缝模型即是在接缝面处另设接缝单元,根据现有的有限元模型研究成果,接缝单元模型可以选择如下形式:分离式平面模型、分离式实体模型和截面模型。分离式平面模型一般用于二维平面结构,采用四节点等参元,单元厚度很小,如图1(a)所示;分离式实体模型一般用于三维立体结构,采用八节点等参元,单元厚度仍然很小,如图1(b)所示;截面模型根据所选定自由度的不同可分别用于二维或三维结构中,截面允许沿不同自由度被赋予不同的材料性能,如图1(c)所示。图中整体坐标系为Oxyz,单元局部坐标系为O＇d1d2d3,其中d1沿缝的厚度方向,d2、d3沿缝面方向,单元坐标系与整体坐标系夹角为α。

根据施工缝的特点,可选取3种接缝单元模型中的截面模型来模拟施工缝。截面模型根据被赋予的材料属性不同,可以模拟施工缝不同自由度的力学性能,并且截面模型可以运用纤维截面(fiber section)的相关研究成果,通过选用合适的材料单轴本构关系即可达到较高精度的计算结果。有关施工缝模型的基本描述,可参考文献[15],下面只选取与本文相关内容作简要说明。

图1 3种接缝单元模型

施工缝具有独特的受力特点,主要由接缝面混凝土和穿过缝面纵向钢筋两部分来承担。混凝土法向不能传递拉应力,只能传递压应力和剪应力;纵筋可以传递拉应力、压应力和剪应力。另外,轴力会显著影响施工缝的力学性能,建立的施工缝模型必须能准确体现这一点。基于此,该施工缝模型以纤维截面模型为基础。但是单纯的纤维模型无法考虑剪切效应,而施工缝处的剪切性能是另一个不容忽视的重要参数。建立的施工缝模型必须能同时考虑法向拉压性能和切向剪切性能,施工缝模型的剪切性能可以由试验中得到的能反映施工缝周围区域平均剪切效应的基于截面的剪切恢复力模型来描述。这样做的优点是避开了分析不同组分在施工缝处复杂的剪力传递机理,大幅度减小了工作量,且能对施工缝的剪切恢复力关系进行综合描述,缺点是无法考虑剪力与轴力、弯矩的耦合作用。

法向受力性能由界面拉压弹簧(interface-TC spring)描述,切向受力性能由界面剪切弹簧(interface-shear spring)描述,由此,建立的施工缝模型就能同时考虑切向剪力性能和法向拉压力性能,如图2所示。由于施工缝沿轴向没有长度,节点i、j之间距离设为0,界面拉压弹簧的属性通过定义纤维截面来实现,对混凝土纤维和钢筋纤维分别选择符合施工缝处接缝混凝土力学特点和穿过缝面钢筋力学特点的材料本构模型。混凝土纤维划分为核心区混凝土和保护层混凝土,核心混凝土通过计算加强系数来考虑箍筋的影响作用。界面剪切弹簧的属性通过定义基于施工缝处截面的剪切本构模型来实现。关于施工缝模型的刚度矩阵推导详见文献[15]。

图2 施工缝模型

2 施工缝模型在数值计算中的应用

建立数值模型的另一个重要步骤是完成其与有限元软件的衔接,即解决力学模型的应用问题。本文以OpenSees软件为平台,按照OpenSees中的建模流程[16]说明如何应用施工缝模型进行非线性分析。该程序内部源码完全开放并具有面向对象编程的特点,用户可以根据实际情况,自主加入新的单元类型、改进材料的本构关系、实现更高效的迭代方法等。核心代码按功能可分为三大模块,即建立有限元模型、进行(非)线性分析和控制输出计算结果。具体步骤如图3所示。

图3 带缝柱数值分析流程

3 施工缝模型的验证

按照上述建模流程,对4根带缝柱拟静力试验[17]以及两榀RC平面框架试验[18]进行数值模拟,通过数值计算与试验结果的对比,验证施工缝模型的合理性和有效性。

3.1 材料本构模型及参数取值

对于纤维截面模型来说,纤维材料本构模型的选取对整个数值分析的结果至关重要。OpenSees中现有的材料对象非常丰富,本文计算中选用concrete01和concrete02两种混凝土材料,钢筋材料选用steel01和steel02。关于选用的混凝土和钢筋材料本构关系详细描述见文献[15],均是与试验结果吻合较好且计算效率较高的模型。选用Bond_SP01模型[19]描述施工缝处的钢筋滑移特性,该钢筋滑移本构模型可用于模拟钢筋混凝土构件端部(如柱、剪力墙与基础相交的根部或构件之间的交界处)转动引起的纵筋滑移,是沿锚入相邻构件的纵筋的应变渗透作用。施工缝处的剪力传递机制比较复杂,可以看做缝面混凝土的摩擦力和纵筋的销栓作用的集合,与轴向荷载、钢筋与混凝土强度、纵筋配筋率等均有很大关系。文献[15]结合试验提出的基于截面的剪切恢复力模型可用于描述施工缝周围塑性铰区的综合剪切性能。本文计算的模型均取自试验中的试件,非线性分析中钢筋和混凝土材料的参数均取自试验中的实测值。

3.2 带缝柱的数值模拟

文献[17]对一组根部带有施工缝的钢筋混凝土柱进行了拟静力试验,主要考察施工缝对柱抗震性能的影响,试件的尺寸及配筋如图4所示。

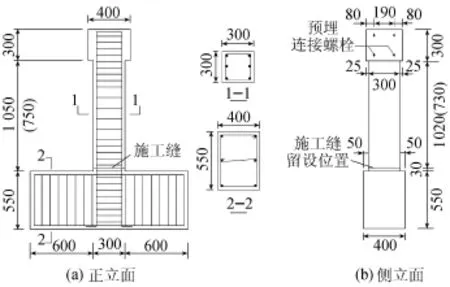
图4 试件尺寸及配筋(单位:mm)

为了验证加入施工缝模型后的计算效果,对各试件均按照加入施工缝模型和传统的不考虑施工缝影响的方法分别建模计算(以下分别简称为带缝模型和传统模型)。虽然试验中测量数据显示整浇柱的剪切变形分量所占比重比带缝柱小,但是本身也不可忽略,因此,传统模型中对非线性梁柱单元加入弹性剪切材料以近似考虑剪切变形的影响。各构件正反向(即推和拉)最大荷载的计算值与相应试验值的对比及误差分析见表1,各构件的力-位移滞回曲线对比结果见图5。

表1 最大荷载的计算结果与试验结果比较

图5带缝柱力-位移滞回曲线试验结果与数值计算结果对比

由表1、图5可见,按照带缝模型计算的最大荷载值与按照传统模型计算的值相差不大,均与试验结果较为接近,误差一般不超过10%。其中两种模型计算的正向(即推)最大荷载均与试验结果更为相近,而反向(即拉)最大荷载均与试验结果相差较大,这一方面是因为数值计算中无法很好地模拟裂缝因闭合而重新参与受力以及钢筋的“包兴格效应”;另一方面是因为试验中的加载制度在位移控制阶段,是根据屈服位移的整数倍来控制位移增长幅度的,而正反向的屈服位移一般并不相同,这也造成后达到屈服的反向最大荷载比较大。

但是两种模型的计算结果在模拟力位移滞回曲线的走势规律上差别明显,按照带缝模型计算的结果与试验数据吻合得比较好。分析其原因,主要在于传统模型忽略了施工缝的影响,无法考虑沿施工缝的剪切错动以及缝面开裂后钢筋较大滑移所造起的捏缩现象。

3.3 平面框架的数值模拟

对文献[18]完成的两榀RC平面框架试验进行数值模拟。文献[18]试验试件采用两层两跨的RC平面框架,框架的尺寸和配筋如图6所示。共制作两个试件,一个是整浇框架,编号MF;另一个是带施工缝框架,施工缝留设在每层柱底部与梁上表面交界处(图中CJ),编号FCJ。试验采用低周反复加载,边柱和中柱对应试验轴压比分别为0.171和0.267,水平加载制度采用力与位移混合控制方法,构件屈服以前采用力控制,每级荷载循环1次,构件屈服以后采用位移控制,级差为屈服位移的整数倍,每级荷载下循环3次。

图6 框架尺寸及配筋(单位:mm)[18]

对两榀框架分别建模进行数值模拟,梁和柱选用基于柔度法的非线性梁柱单元,单元截面采用纤维截面。截面纤维离散时采用较为均匀的划分方式,梁与柱截面均区分保护层混凝土与核心混凝土,对核心混凝土通过约束加强系数考虑箍筋的影响作用。截面纤维数目需达到一定数量才可认为数值积分结果的精度满足要求,本文分析中柱截面核心混凝土纤维划分为10×10,梁截面核心混凝土纤维划分为4(宽)×20(高),这样即认为有足够的计算精度。柱和梁纤维截面的划分如图7所示,其中施工缝模型的纤维截面划分与对应的柱截面一样。

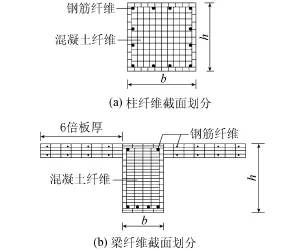
图7 柱和梁纤维截面划分

带缝框架在施工缝位置加入施工缝模型,参数取试验实测值。两个框架顶层力位移滞回曲线的试验值和数值模拟结果对比如图8所示,最大荷载对比结果如表2所示。

表2 最大荷载的计算结果与试验结果比较

由表2和图8可见,两个框架顶层的滞回曲线的数值模拟结果基本与试验结果一致,但是试验滞回曲线有明显下降段,数值模拟的滞回曲线未出现明显下降段。就最大荷载而言,计算结果与试验结果相差不大,最大不超过10%。由于本文更关心的是带缝框架与整浇框架的对比情况,由计算结果可见,带缝框架的最大荷载计算值比整浇框架低,但相差不超过2%,与试验情况基本相符;带缝框架的力位移滞回曲线比整浇框架捏缩明显,能反映整浇框架的耗能能力略好的试验结果;两个框架的相对变形相差不大,与试验结果一致。因此,可认为本文选用的整体框架数值建模方法基本比较合理,施工缝数值模型的应用基本能与试验结果保持一致。

4 结 语

对带缝柱的数值计算结果显示,应用带缝模型计算结果与试验结果吻合较好。而传统模型由于忽略施工缝的影响,无法考虑沿施工缝的剪切错动以及缝面开裂后钢筋较大滑移所造起的捏缩现象,在模拟滞回曲线的走势规律上与试验结果差别较大。两榀平面框架的顶层力位移滞回曲线的数值计算与试验结果一致,尤其体现在带缝框架与整浇框架在最大荷载和力位移滞回曲线特点上的差别,该施工缝数值模型的应用能使计算结果与试验结果保持一致。

图8框架顶层力位移滞回曲线试验结果[18]与计算结果对比

[1]WATERS T.A study of the tensile strength of concrete across construction joints[J].Magazine of Concrete Research,1954,6(18):151-153.

[2]宋玉普,魏春明.混凝土施工缝接缝面劈拉强度试验研究[J].混凝土,2006(6):22-25.(SONG Yupu.WEIChunming.Experimental research on the splitting tensile strength for joint surface of concrete construction joint [J].Concrete,2006(6):22-25.(in Chinese))

[3]MONKSW L.Treatment of construction joints[J]. Concrete,1974,8(2):28-30.

[4]ISAO U,YOSHIDA N,MORISHITA S.Evaluation of mechanical properties of construction joint between new and old concrete under combined tensile and shear stresses[J].Journal of the Society of Materials Science, Japan,1998,47(1):73-88.

[5]MATTOCK A H.Cyclic shear transfer and type of interface [J].Journal of the Structural Division,ASCE,1981,107 (10):1945-1964.

[6]张卫东,王振波,朱方之.施工缝位置对框架结构抗震性能的影响[J].低温建筑技术,2007,118(4):46-48. (ZHANG Weidong,WANG Zhenbo,ZHU Fangzhi. Influence of position of construction joint on seismicresistance behavior of reinforced concrete frame[J].Low Temperature Architecture Technology,2007,118(4):46-48.(in Chinese))

[7]李通林,王艳辉.结构面非线性剪切模型的探讨[J].重庆大学学报,1990,13(3):54-59.(LI Tonglin,WANG Yanhui.An investigation on nonlinear shear model of discontinuity[J].Journal of Chongqing University,1990, 13(3):54-59.(in Chinese))

[8]段云岭,刘华北.材料非线性接缝模型[J].清华大学学报:自然科学版,2000,40(8):98-101.(DUAN Yunling, LIU Huabei.Materialnonlinear jointmodel[J].Journal of Tsinghua University,2000,40(8):98-101.(in Chinese))

[9]孙吉主,施戈亮.循环荷载作用下接触面的边界面模型研究[J].岩土力学,2007,28(2):311-314.(SUN Jizhu, SHIGeliang.Bounding surface model for soil-structure interface under cyclic loading[J].Rock and Soil Mechanics,2007,28(2):311-314.(in Chinese))

[10]CLOUGH GW,DUNCAN JM.Finite element analysis of retaining wall behavior[J].Journal Soil Mech&Found Engrg Div,ASCE,1971,97(12):1657-1674.

[11]BRANDT JR T.Behavior of soil-concrete interfaces[D]. Edmonton:The University of Alberta,1985.

[12]DESAIC S,DRUMM E C,ZAMAN M M.Cyclic testing and modeling of interfaces[J].Journal of Geotechnical Engineering,1985,111(6):793-815.

[13]DESAIC S,MA Youzhi.Modeling of joints and interface using the disturbed state concept[J].Journal for Numerical and Analysis Methods in Geomechanics,1992, 16:623-653.

[14]BOULON M,NOVA R.Modeling of soil structure interface behavior:a comparison between elastoplastic and rate-type laws[J].Computers and Geotechnics,1990,17(9): 21-46.

[15]李英民,于婧,夏洪流.施工缝模型及在钢筋混凝土柱非线性分析中的应用[J].土木建筑与环境工程,2011, 33(5):1-6.(LI Yingmin,YU Jing,XIA Hongliu. Construction joint modeling and its application in nonlinear analysis of RC columns[J].Journal of Civil, Architectural&Environmental Engineering,2011,33(5): 1-6.(in Chinese))

[16]MAZZONIS,KENNA F M,SCOTT M H,et al.Opensees users manual[R].Berkeley:PEER,University of California,2006.

[17]李英民,于婧,夏洪流.施工缝对框架柱抗震性能影响的试验研究[J].土木工程学报,2011,44(增刊1):81-86.(LI Yingmin,YU Jing,XIA Hongliu.Experimental research on seismic behavior of frame columns with construction joint[J].China Civil Engineering Journal, 2011,44(Sup1):81-86.(in Chinese))

[18]魏春明.现浇钢筋混凝土框架结构施工缝抗震性能[D].大连:大连理工大学,2006.

Verification of construction joint numerical model

YU Jing,LIU Xiaojun(College of Civil Engineering,Xi’an University ofArchitecture and Technology,Xi’an 710055,China)

In order to solve the problem of construction joint simulation in numerical calculation of reinforced concrete structure,according to the existing research,a suitable model was chose based on the formation and stress features of construction joint.Related research of fibermodel,the average of shear effect in peripheral region of construction joint,as well as normal and tangentialmechanical propertieswere comprehensively considered in themodel.By using the OpenSees software,numerical calculation of pseudo static tests on four columns with construction joint and two plane frames was performed and the modeling flow was proposed.The test results of maximum load and the law of force-displacement hysteretic curves and the calculated results showed:the construction jointmodel could simulate the shrinkage phenomenon due to shear slide along construction joint face and the far steel bar-slip.The test results are in close agreement with the calculated results,thus confirming the rationality and validity of the construction jointmodel.

construction joint;joint element;reinforced concrete structure;OpenSees software;numerical model; modeling verification

TU375

A

1006-7647(2015)02-0037-06

10.3880/j.issn.1006 7647.2015.02.008

2014-04-29 编辑:熊水斌)

国家自然科学基金(51208407);西安建筑科技大学人才科技基金(RC1233)

于婧(1982—),女,河南开封人,讲师,博士,主要从事混凝土结构防震减灾研究。E-mail:yujing1506@163.com