明渠紊流与床面形态相互作用研究进展

唐立模,孙会东,刘全帅

(1.河海大学水文水资源及水利工程科学国家重点实验室,江苏南京 210098; 2.河海大学水利水电学院,江苏南京 210098)

明渠紊流与床面形态相互作用研究进展

唐立模1,2,孙会东2,刘全帅2

(1.河海大学水文水资源及水利工程科学国家重点实验室,江苏南京 210098; 2.河海大学水利水电学院,江苏南京 210098)

结合国内外最新研究动态,从明渠紊流与床面形态相互作用的研究方法、明渠紊流特点、紊流对沙波形态的影响、床面形态对紊流的反作用等方面对明渠紊流与床面形态相互作用进行了综述。当前明渠紊流特性、二维沙波床面水沙运动特性等方面的研究已经取得丰富成果,但尚不能很好地解释天然河流中的水沙输移机理;由于试验测量方法的限制,复杂床面条件下的水沙相互作用研究在相当长时间内没有取得突破性的成果,亟需探索和引入无干扰、高精度的三维瞬态全场测量技术;床面几何形态、沙波发展演变方面的研究相对成熟,但床面的稳定机理尚存在分歧,理论模型和数学模型均不够完善,尤其沙波内部渗流与明渠紊流综合作用下的床面稳定性和泥沙运动特性研究还比较少,是今后进一步探索的方向,其成果可为揭示三维沙波床面紊流与泥沙相互作用机理提供必要的前提。

明渠;紊流结构;紊动特性;床面形态;沙波演变;综述

天然河流的流态常见为紊流,床面附近的近壁区是紊流研究的重要区域,水流相干结构的产生、沙波床面的形成与发展都是在这一区域发生。近壁区域的水流运动是河流泥沙运动的能量来源,使得河道床面形态发生改变,形成沙纹沙垄等各类床面形态。相应地,床面形态的存在也改变了冲积河流的水流结构,对水流阻力和泥沙输移均产生影响。水流结构与床面形态相互作用、相互影响,研究二者间的相互作用机理是泥沙运动力学的基础理论课题,其成果对于研究明渠泥沙输移机理、河道冲淤演变规律以及河道中污染物输移机制等课题都有重要意义。本文总结分析了近年来明渠紊流与床面相互作用的研究成果,并对这一问题的研究方向进行了展望。

1 明渠紊流与床面形态相互作用的研究方法

目前,明渠紊流结构与床面形态相互作用的研究方法主要包括试验研究和数值模拟两大类,试验研究又分为定床试验和动床试验。定床试验通过概化二维或三维床面形态模拟真实床面,动床试验是在床面铺沙且形成床面形态条件下研究紊流结构、分析床面形态特征。定床条件由于对真实床面做了简化且少了床面这一可动边界,紊流结构较易测量,但是其结果和真实床面有差异;对动床情况,床面边界可动给紊流观测带来很大的困难,目前动床试验主要用于研究床面的形态特征、床面发展演变等。紊流结构的测量仪器包括:声学多普勒流速仪(ADV)、粒子图像测速仪(PIV)、激光多普勒流速仪(LDV)等,床面特征的测量可以采用超声地形仪测量、停水后用测针测量和用摄像机拍摄测量等方法。

数值模拟在精确模拟床面形态、增强流场可视化效果、节约试验成本等方面有着独特的优势。常用的数值模拟方法有直接数值模拟(DNS)法和大涡模拟(LES)法。直接数值模拟计算结果准确,但计算量大,只适用于小雷诺数和中等雷诺数情况,不适用于较高雷诺数情况;大涡模拟由于对控制方程进行了简化,精度要低于直接数值模拟。Bhagangar等[1]在摩阻雷诺数Re子=400时,采用DNS法模拟计算了床面粗糙形态对水流的影响;Robert[2]采用DNS法研究了雷诺数对明渠水流的影响,其模拟最大雷诺数达到590;Imran[3]通过DNS法研究了Re子=619时,床面存在凸起条件下涡结构的特性,其对涡结构的模拟需要更大的计算量。从这些研究的计算条件可以看出,直接数值模拟方法受到计算量的限制,摩阻雷诺数只能局限于中等强度,有一定的局限性。在大涡模拟方面,Bomminayuni等[4-6]成功地模拟了粗糙床面、二维概化沙纹条件下的紊流结构,他们的计算成果都和相应的实验数据吻合良好,但尚未扩展到动床条件下的模拟。

2 明渠紊流特点

2.1 明渠紊流的时均流速

Nezu等[7]对光滑明渠水流进行了研究,根据水流距壁面的距离将水流分为主流区和近壁区,以壁面的法向为y向,水深为h,y/h＜0.2的区域称为近壁区,y/h≥0.2的区域称为主流区;又将近壁区分成黏性底层、对数区、过渡区三部分。各区的流速分布见表1,表中:

式中:U为瞬时流速;U*为摩阻流速;ν为运动黏滞系数;h为水深。表1中κ、A、П为常数,其中A= 5.29±0.47,κ=0.412±0.11,随着底坡或弗劳德数的增加,A有减小的趋势,陈兴伟等[8]认为样本容量对A值有一定的影响,样本容量增大时,A更趋于稳定。

表1 流速垂线分布

2.2 明渠紊流的紊动特性

Nezu等[9-11]对明渠紊动强度进行了研究,认为各个方向的紊动强度与相对水深成指数关系,边壁附近处因受空间的限制,紊动强度为零,离边壁稍远,紊动强度迅速增大达到一个峰值,主流区垂向紊动强度接近摩阻流速,纵向紊动强度大于垂向紊动强度。Song等[12]对挟沙情况下的明渠水流紊动特性进行了研究,同样得出紊动强度沿水深符合指数分布的结论。

Nezu等[9-11]还分析了明渠紊流的雷诺应力分布规律,认为近壁区由于黏性底层的影响,雷诺应力从床面开始由零增加到最大值,该极值一般位于0.1～0.2倍水深处,然后垂向正向呈线性递减趋势,在自由水面处减小到零,雷诺应力在外区服从线性分布。Yang[13]通过理论分析建立了雷诺应力与床面剪切力和速度分布的理论模型,并根据实测雷诺应力值和速度分布情况来反推床面剪切力,这是传统的测量方法很难做到的。Auel等[14]通过LDV试验研究了非恒定流条件下的雷诺应力影响因素,认为雷诺数和弗劳德数对雷诺应力分布不产生影响,而宽深比对其影响明显,边壁处的雷诺应力比中心处大20%～50%。

2.3 明渠紊流的紊流结构

毛野等[15]采用流场综合分析法将流动显示与计算机图像处理相结合,对紊动猝发现象进行了研究,结果表明雷诺数增大时,喷射更多的由单体喷射变为群体喷射,喷射角度、喷射和清扫的尺度有增加的趋势。紊流的猝发是拟序的,但是紊流发生的时间和位置是随机的,前人大多采用平均猝发周期来反映猝发的频率。Noguchi等[16]通过PIV试验对清水条件下喷射和清扫的平均猝发周期进行了研究,统计认为平均猝发周期的概率分布服从对数分布,喷射和清扫的平均周期几乎相等,TUmax/h≈1.83。

以往研究表明,涡结构是紊流内部的大尺度结构,发夹涡是一种用来描述紊流相干结构演变的模型。Adrian[17]认为发夹涡的发展模型能够作为涡量传输、近壁区动量传输和紊动能传输的一种解释方式,但是水流紊动并不是完全由发夹涡导致,因为流速梯度也能够产生水流紊动。Herpin等[18]对流向涡进行了研究,得出相似的结果,并认为在床面附近各涡之间相互影响强烈,当距床面超过一定距离时,各涡相互独立;同时还建立了涡密度模型,即随着水深的增加,涡密度增加,并有相同的旋度,流向涡和横向涡的涡半径在不同的雷诺数下,无量纲值的变化趋势是一致的,但受空间分辨率的影响其绝对值不同,涡半径随水深的增加而增加,在对数区增长缓慢。Roussinova等[19]通过正交分解法对明渠紊流的紊动猝发和涡结构进行了分析,结果显示均匀动量区的空间变化与涡结构的运动相匹配,流动显示结合象限分析法更能从本质上分析涡结构对紊流的影响。

由以上分析可知,对明渠紊流的研究目前已经取得相当多的成果,对流速分布规律、紊动特性分布规律等也已经较全面地了解,但对紊流拟序结构的研究,定性研究较多,定量研究成果尚未获得共识,紊流结构的产生机理还不明确。随着逐渐成熟的二维、三维PIV流场瞬时测量技术的发展,通过对流场样本的大规模采集和数据统计分析,紊流拟序结构研究有望取得更多的突破。

3 紊流对床面形态的影响

天然河道中,随着水流的增强,河流床面会出现沙纹、沙垄、平整过渡、逆行沙垄等不同形态。研究紊流对床面形态的影响,主要包括床面发展不同阶段几何形态特征研究、床面形态随时间发展变化研究、沙波的形成与演化机理研究等方面。

3.1 沙波几何形态的影响因素

3.1.1 小沙纹的几何形态

小沙纹是床面发展成沙纹之前的状态,在缓流条件下形成,小沙纹随时间的推移发展成沙纹、沙垄。Coleman[20]通过实验得出小沙纹的表达式:

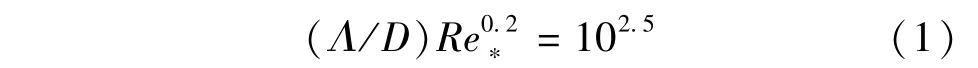
该式不适用于层流。随后Coleman等[21]又给出了小沙纹适用层流条件的表达式:

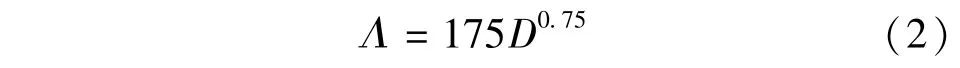
式中:Λ为小沙纹波长;D为泥沙粒径;Re*为沙粒雷诺数。由式(1)和式(2)可知,明渠层流和紊流条件下,小沙纹的产生有一种相似的机制,水流紊动的研究是小沙纹成因分析的基础,水流特性和沙纹形成存在着内在的相关关系。Rauen等[22]通过渐变宽度的水槽试验,统计分析得出小沙纹的高度符合对数正态分布,小沙纹的最大高度为7mm,波高表达式可写为

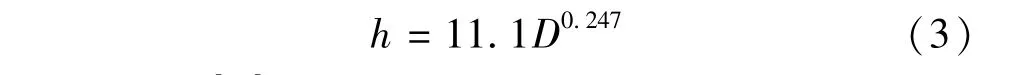
此外,Baas[23]也进行了此方面的研究,获得了类似的成果。

3.1.2 沙纹的几何形态

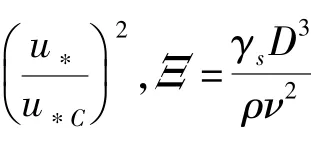
3.1.3 沙垄的几何形态

沙垄属于大尺度床面形态,沙垄的波长正比于水深。van Rijin[27]针对低水流能态区和过渡区的沙垄床面形态,提出了明确床面形态尺度的方法,得出的沙垄波长Λd≈7.3h;Yalin等[24]通过大量试验分析得出沙垄波长Λd≈6 h,二者的结论很相似,认为沙垄的波长和水流相干结构的水平猝发长度相同,这说明水流结构和床面形态有一定的相关性。

Mark等[28]通过水槽试验研究沙波形态,结果表明当宽深比大于10时,床面形态特征值(包括各个点的波高、波长、波峰的高度、波谷的高度)的平均值与标准差呈线性关系,宽深比小于10时呈指数关系;当选取床面特征值的概率密度在95%以上的值来估算床面特征值时,床面形态特征值的平均值与其标准差呈线性关系,其结论在工程上有较好的应用。Coleman等[29]通过水槽试验统计分析各类床面各个位置的床面高度,同样认为沙波的波高平均值是其标准差的函数,并通过床面高度偏态系数和峰态系数来判别不同的床面形态(平整、沙纹、沙垄等),床面稳定时,偏态系数和峰态系数趋于定值。

3.2 沙波随时间的发展

床面从平床发展到稳定的过程中,沙纹、沙垄的形态随时间的变化而变化,大量研究表明,沙波随时间的发展变化受床面初始状态、泥沙粒径、摩阻流速等因素影响。Singh等[30]通过试验研究沙波的发展过程,利用声学仪器记录运动沙波的瞬时波高,发现床面形态发展初期床面发展得更快,小粒径泥沙、流量较小的水流更有利于通过非线性理论准确地预测床面形态。Coleman等[31]通过大量试验得到了初始床面为非平床的床面几何形态随时间变化的表达式:

式中:tefc为从初始状态到稳定状态的时间;t为初始状态到床面稳定之前任意床面状态的时间;P为任意时刻沙波形态参数(波长或波高)的平均值;Pi、Pe为初始和平衡状态下的沙波形态特征参数的平均值;D50为泥沙中值粒径;ρs为泥沙密度;ρ为水的密度;ν为运动黏滞系数。

Raudkivi[32]对床面从平床发展到稳定的时间进行了研究,认为床面在一定水流条件下达到稳定的时间取决于床面切应力的大小和沙粒的粒径,得出冲淤平衡的时间表达式为

式中:te为冲淤平衡时间;a、b为系数,a=1 000、230、6800,b=3.0、2.4、4.3,对应的泥沙粒径D= 0.095mm、0.16mm、0.238mm;θ为无量纲切应力; θc为泥沙起动的临界切应力。Raudkivi试验的泥沙粒径组次较少,难以代表一般规律。Coleman等[31]通过大量试验给出了冲淤平衡时间的幂指数表达式:

式中t*为无量纲化的冲淤平衡时间。Coleman的公式试验组数更多、粒径选择范围更广,有更广泛的适用性。

3.3 沙波的形成机理

床面附近局部扰动引起的近壁流层波动、床面受力不平衡、紊流拟序结构等因素都会影响床面的冲淤和沙纹的形成。冲积河流的河床是由松散的、大小不等的泥沙颗粒组成的,要想保持河床表面的绝对平整是不现实的。另一方面,水流的紊动性质使床面的水流强度因时因地有所不同,当某一点的紊动强度忽然增加到一定程度时,水流即从河床带起泥沙产生冲刷,而在稍下游的地方,紊动强度没有那么大时,又会造成淤积。随后淤积造成水流分离,使得同样的冲刷淤积过程继续向下游延伸,最后形成一系列的起伏。

关于沙波的形成机理,国内外不少学者提出了各自的理论模型,并通过实验数据进行了验证。Ji等[33]引入了恒定涡输运方程和Bagnold泥沙输运方程,用非线性理论来描述紊流和泥沙输移,认为非线性理论能更合理地解释床面的形成。Zhou等[34]在低流态下,运用线性和非线性的普通差分模型,得出了从泥沙起动到平衡的过程中,沙纹波长和波高的变化规律,也认为非线性模型更好。Franklin[35]发展了三维沙纹不稳定理论,认为沙纹模型中最不稳定的是纵向模型,纵向模型和倾斜模型相结合能够建立沙纹的三维模型,并在模型中考虑了不稳定涡的作用。白玉川等[36]认为,沙纹的尺度较小,主要由明渠层流不稳定性和床面附近层流的小尺度拟序结构发展演化所致,如果扰动产生的切应力接近床面泥沙固有频率,则泥沙颗粒产生共振,床面发生最大的响应,沙纹发展速度最快。Colombini等[37]通过线性理论的方法分析了沙纹沙垄的形成机理,认为沙纹、沙垄的形成是因为床面形态相对剪切力的滞后,沙纹是在较小的沙粒雷诺数和希尔兹数下形成的,沙垄是在较大的沙粒雷诺数和希尔兹数下形成的,沙波的成因与希尔兹数、沙粒雷诺数、弗劳德数、粗糙雷诺数都有关。

4 床面形态对紊流的影响

沙纹、沙垄是天然河流中常见的床面形态,床面形态从根本上改变水流的边界,对水流结构产生明显的影响。掌握各种床面形态下的紊流结构特点是研究床面对水流响应的基础,也是进一步研究水沙相互作用的基础。

4.1 床面粗糙度对紊流的影响

床面粗糙导致了紊流在空间上受位置的影响,特别是在高雷诺数、小水深条件下,床面粗糙度对水流紊动特性、涡结构、床面阻力均产生重要的影响,但由于床面形态的多样性,床面等效粗糙度等问题还存在不同的看法。

Bhagangar等[1]通过DNS法研究床面粗糙度对水流紊动特性的影响,认为床面粗糙区的高度为床面突起高度的1.1倍,粗糙体的尺寸决定紊流能否影响到外区,床面粗糙使得紊流各个方向的紊动强度降低,紊动强度的峰值减小,使低速带的宽度增加,流向涡的半径增大,涡在垂向上延伸得更远。Bomminayuni等[4]用LES方法模拟床面粗糙度对紊流的影响,用象限分析法统计了喷射和清扫在雷诺应力和异性湍流中占的比例,认为粗糙床面的紊流异性比光滑床面要小,紊流特性方面的结论与Bhagangar的结论基本一致,紊动强度峰值随着粗糙度增加而减小,但是横向紊动强度变大,这与Bhagangar的结论不同,可能是他们在模拟中选用了不同形状和不同分布的粗糙体导致的。Roussinova等[38]认为,紊流异性和床面粗糙体的间距p与高度h的比值有关,p/h的值决定了紊流异性增大还是减小,粗糙体的密度与分布对紊流的影响很重要。王宪业等[39]通过水槽试验对粗糙床面的阻力进行了研究,得出了床面阻力与雷诺数、相对粗糙高度的关系,认为粗糙床面阻力增加,能量由平均流速向紊动能转化,并对Rouse的床面阻力系数公式做了进一步的改进,赵锦程等[40-41]也分别获得了和王宪业类似的结论。

床面粗糙度对明渠紊流喷射角度、喷射和清扫的尺度以及平均猝发周期等有很大影响。毛野等[15]采用流场综合分析法将流动显示与计算机图像处理相结合,在不同表面糙率的条件下重点研究了紊流的猝发形态和特性,结果表明增大粗糙雷诺数使群体喷射现象增多,喷射角度、喷射高度、平均猝发周期、喷射尺度以及清扫尺度均趋于增大。Imran[3]通过DNS法模拟了粗糙床面下的涡结构变化,研究表明在水流分离和压力梯度的作用下,涡的密度增加,涡半径减小,说明产生了新的涡,同时涡的平均尺度发生了调整。Hardy等[42]通过流动显示技术(DPIV)研究了粗糙床面的相干结构,并通过小波分析法计算分离区的长度,认为床面粗糙引起的水流尾迹摆动是产生大尺度相干结构的直接原因,同时还研究了雷诺数对大尺度结构的影响,随着雷诺数增大,相干结构更明显,紊动强度也更大。

4.2 沙波床面对紊流的影响

沙波顶部会产生边界层水流分离,在波峰和再附着点之间形成回流区,波谷附近的低速流体和它上层的高速流体相互作用,形成了剪切混合层,演变成猝发、喷射、泡漩等现象。沙波附近的紊流结构对冲积河流的泥沙运动有重要的作用。

4.2.1 沙波形态对紊流特性的影响

沙波床面的流速分布不同于平床,回流区内流速分布不再符合对数律,产生了负值。在外区,不同沙波形态下的流速和雷诺应力与平床情况基本相同。Noguchi等[43-44]在运动沙波床面上测量了不同时间、不同床面位置处的水流瞬时流速,认为波峰处的时均流速较明渠变化不大,波谷处由于反向流的作用,时均流速变化较大;随着沙波的发展,波峰的流速有增大趋势,再附着点和波谷处的流速受水流回流的影响而变得更小,背水面的紊动强度和雷诺应力增大。Omidyeganeh等[45]利用大涡模拟的方法研究了三维沙垄床面紊流,通过改变沙垄的波峰变形幅度、沙垄波长,分析它们对紊流结构的影响,结果表明:沙垄波峰处的流动分离改变了壁面压力分布,也导致了高动量流体结构和低动量流体结构在床面的重新分布,三维床面增加了床面的水流拖曳力,无量纲化的紊动能较二维情况小。Xie等[6]通过大涡模拟研究了二维沙垄床面的紊流特性,认为沙垄床面产生的紊流受自由表面变形的影响,通过比较表面可变形法和表面约束法,提出考虑表面变形的方法更准确,其模拟在高雷诺数、小水深下完成,很好地体现了二次流的作用。

4.2.2 沙波对再附着点的影响

床面形态影响水流的分离长度,回流区的大小由波长、波高和水流强度决定。Liu[46]通过改变沙波模型的波长和波高进行了试验,分析认为波高越大,水流分离长度越大,分离长度是波高的4.2～7.74倍;López等[47]通过概化模型模拟了沙纹到沙垄过渡的过程,得出分离长度为3.7～5.9倍波高的结论。两者的研究成果有所差异,是因为试验过程中,模型的尺寸、水流的强度都不尽相同。对于真实沙波床面的情形,Noguchi等[43-44]实测了沙波形成各个阶段的水流特性,分析了沙波形态的影响,认为随着沙波的发展,分离长度增大,最后趋近于5.5倍波高。

4.2.3 沙波床面对紊流高阶矩的影响

床面形态对高阶矩的影响主要包括对紊动产生项、紊动消耗项、紊动能的影响。紊动产生项值的大小反映能量从平均流速向紊动能转化的多少,紊动消耗项则反映紊动能损失的多少。Noguchi等[43]研究了床面形态对紊动产生项和消耗项的影响,指出紊动产生项在水流分离处最大,紊动消耗项在回流区最大,说明紊动能在水流分离处产生的更多,在回流区消耗的更多。López等[47]通过改变床面形态模拟沙纹到沙垄过渡的过程,发现在床面发展过程中紊动产生项的值增大,认为紊动对床面的发展起促进作用。

4.2.4 沙波床面对紊流结构的影响

沙波顶部的水流分离产生了分离涡,剪切层内的水流向内作用形成清扫,向外作用形成泡漩。Stoesser等[5]利用大涡模拟计算研究了二维沙波附近的水流结构,认为在再附着点附近,因为二次流的不稳定性,流线弯曲并且向外运动导致泡漩涡发展成发夹涡。Nezu等[48]研究了沙波背水面的三维涡结构,认为分离涡的平均周期随雷诺数的增加而减小,泡漩涡的平均周期随雷诺数的增加而增加;泡漩涡的涡强度更大。毛野等[15]通过概化沙纹试验,研究得出分离涡的平均周期为0.46 s。Liu[46]研究了沙波形态对涡脱落周期的影响,认为波高越大,涡脱落周期越长。Chang等[49]通过改变沙垄的形态研究发夹涡的产生机理,提出发夹涡是由床面附近的干扰导致的,并对带状结构的形成起到了关键作用,非对称的沙垄形态更有利于发夹涡的形成。Keshavarzi等[50]通过水槽试验结合图像处理技术研究了沙纹床面的紊流结构,发现清扫的发生频率与沙波形态变化趋势一致,而喷射的发生频率与沙波形态变化趋势不一致,提出泥沙的运动是被清扫作用控制的,并据此解释了沙波迎水面冲刷、背水面淤积的现象。

4.2.5 运动沙波床面对水流结构的影响

Gyr等[51]研究了泥沙运动对水流的影响,认为泥沙输移使流速偏离对数律的程度减小,对摩阻流速的影响可达到30%;同时泥沙输移使得清扫的强度更高,沿垂向分布更加均匀,清扫的平均猝发周期则不受影响。Dey等[52]研究了泥沙刚刚起动时其对水流的影响,提出运动床面流速比定床更接近对数律的原因是紊动产生项更小,从而更少的能量从平均流速转移到紊动能,使得流速更小地偏离对数律;同时还分析了清扫强度加大的原因,认为流向和垂向向下的雷诺应力分量增大,流体更多地向前、向下运动。

5 总结及展望

拟序结构的发现为明渠紊流研究注入了新的活力,随着流动测试技术的发展,紊流拟序结构的内在机理研究正在逐步深入,这为床面形态和床面稳定的研究奠定了更坚实的基础。由于水沙相互作用的复杂性,还有很多机理性的问题没有得到解决。笔者认为今后应在以下几方面开展进一步研究:

a.三维床面形态对紊流结构的影响。目前沙波床面的研究多数采用二维概化模型,而天然河流中的床面形态多为三维的,这就使得当前多数的研究成果并不能真正反映实际河流的水沙运动特性,因此开展三维床面的紊流结构研究具有重要的理论和实践意义。

b.新的流体运动测量技术在水沙运动试验中的应用。目前对于非平整床面上水流结构、泥沙运动的研究,更多采用的是数值模拟方法,试验研究由于受到测量方法的限制,在相当长一段时间内没有取得突破性的成果。随着现代流体测量技术的发展,高精度的三维瞬态全场测量方法正在逐步研究完善,如何将其尽快应用于紊流拟序结构和泥沙运动力学试验当中,是今后应进一步努力的方向。

c.沙波床面内部渗流作用对泥沙运动特性的影响。当前大多数有关沙波床面水沙运动的研究,往往只是将床面形态作为一个固定或可动的边界,实际上沙波内部同样存在水流运动,渗流的作用将改变迎水坡、背水坡等不同位置处泥沙颗粒的受力状态,从而使泥沙的起动、扬动特性发生更为复杂的变化。开展明渠紊流与床面渗流综合作用下泥沙运动特性的研究,对于进一步丰富完善泥沙运动力学、河床演变学理论具有重要意义。

[1]BHAGANGAR C,KIM J,COLEMAN G.Effect of roughness on wall-bounded turbulence[J].Flow Turbulence and Combustion,2004,72(2/3/4):463-492.

[2]ROBERT D.Direct numerical simulation of turbulent channel flow up to Re子=590[J].Physics of Fluids,1999, 11(4):943-945.

[3]IMRAN S.Vortical Structures in wall-bounded turbulent flow with recirculation[C]//13th European Turbulence Conference.Lille:IOP Publishing Ltd.,2011:1-15.

[4]BOMMINAYUNIS,STOESSER T.Turbulence statistics in an open-channel flow over a rough bed[J].Journal of Hydraulic Engineering,2011,137(11):1347-1358.

[5]STOESSER T,BRAUN C,VILLABA G,et al.Turbulence structures in flow over two-dimensional dunes[J].Journal of Hydraulic Engineering,2008,134(1):42-55.

[6]XIE Zhihua,LIN Binliang,FALCONER R A.Turbulence characteristics in free-surface flow over two-dimensi-onal dunes[J].Journal of Hydro-Environment Research,2014, 8(3):200-209.

[7]NEZU I,NAKAGAWA H.Turbulence in open channel flows[M].Rotterdam:A.A.Balkema,1993.

[8]陈兴伟,林炳青,林木生.样本容量对明渠垂线流速分布对数公式拟合的影响[J].水利水电科技进展,2013, 33(5):35-37.(CHEN Xingwei,LIN Bingqing,LIN Musheng.Impact of sample size on the log-law fitting of vertical velocity distribution in open-channel flows[J]. Advances in Science and Technology ofWater Resources, 2013,33(5):35-37.(in Chinese))

[9]NEZU I.Open-channel flow turbulence and its research prospect in the 21st century.[J]Journal of Hydraulic Engineering,2005,131(4):229-246.

[10]TAMIMIS.On Turbulent flow near a wall[J].Journal of Communication and Computer,2012,23(11):1104-1109.

[11]NIKORA V,KOLL K,MCEWAN I,et al.Velocity distribution in the roughness layer of rough-bed flows[J]. Journal of Hydraulic Engineering,2004,130(10):1036-1042.

[12]SONG T,GRAF W.H.Velocity and turbulence distribution in unsteady open-channel flows[J].Journal of Hydraulic Engineering,1996,122(3):141-154.

[13]YANG Shuqing.Depth-averaged shear stress and velocity in open-channel flows[J].Journal of Hydraulic and Engineering,2010,136(11):952-985.

[14]AUEL C,ALBAYRAK I,BOES M.Turbulence characteristics in superitical open channel flows:effects of froude number and aspect ratio[J].Journal of Hydraulic Engineering,2014,140(4):278-286.

[15]毛野,杨华,袁新明.表面糙率与明渠紊流猝发现象[J].水利学报,2002,33(6):53-59.(MAO Ye,YANG Hua,YUAN Xinming.Bed surface roughness and bursting phenomena in open channel[J].Journal of Hydraulic Engineering,2002,33(6):53-59.(in Chinese))

[16]NOGUCHIK,NEZU I.Particle turbulence interaction and local particle concentration in sediment-laden openchannel flows[J].Journal of Hydro-Environment Research 2009,3(2):54-68.

[17]ADRIAN R J.Hairpin vortex organization in wall turbulence[J].Physics of Fluids.2007,19(4):4-13.

[18]HERPIN S,STANISLAS M,FOUCAUT J M,et al. Influence of the reynolds number on the vortical structures in the logarithmic region of turbulentboundary layers[J]. Journal of Fluid Mechanics,2013,716:5-50.

[19]ROUSSINOVA V,SHINEEB A M,BALACHANDAR. Investigation of fluid structures in a smooth open-channel flow using proper orthogonal decomposition[J].Journal of Hydraulic Engineering,2010,136(3):143-154.

[20]COLEMAN SE.Initiation of bedforms on a flat sand bed [J].Journal of Hydraulic Engineerin,1996,122(6):301-310.

[21]COLEMAN SE,ELING B.Sand wavelets in laminar openchannel flows[J].Journal of Hydraulic Research,2000,38 (5):331-338.

[22]RAUENW B,LIN B L.Transition from wavelets to ripples in a laboratory flume with a diverging channel[J]. International Journal of Sediment Research,2008,23(1): 1-12.

[23]BAAS J H.A flume study on the development and equilibrium morphology of current ripples in very fine sand [J].Sedimentology,1994,41(8):185-209.

[24]YALIN M A M,FERREIRA DA SILVA.Fluvial processes [M].Delft,the Netherlands:IAHR Monography,2001.

[25]赵连白,袁美琦.泥沙运动规律的试验研究[J].泥沙研究,1995(1):22-33.(ZHAO Lianbai,YUAN Meiqi. Experimental study on sand waves[J].Journal of Sediment Research,1995(1):22-33.(in Chinese))

[26]张瑞瑾.河流泥沙动力学[M].北京:水利电力出版社, 1989.

[27]van RIJIN L C.Bed forms and alluvial roughness[J]. Journal of Hydraulic Engineering,1984,110(12):1733-1754

[28]MARK C F,BLOM A,HULSCHER S J M H. Quantification of variability in bedform geometry[J]. Journal of Geophysical Research,2008(113):3-30.

[29]COLEMAN SE,NIKORA V I,ABERLE J.Interpretation of alluvial beds through bed-elevation distributionmoments [J].Water Resources Research,2011,47(11):505-519.

[30]SINGH A,LANZONI S,WILCOCK P R.Multiscale statistical characterization ofmigrating bed forms in gravel and sand bed rivers[J].Water Resources Research,2011, 47(12):526-552.

[31]COLEMAN S E,ZHANG M H,CLUNIE T M.Sedimentwave development in subcritical water flow[J].Journal of Hydraulic Engineering,2005,131(2):106-111.

[32]RAUDKIVI A.Journal of ripples on a stream bed[J]. Journal of Hydraulic.Engineering,1997,123(1):58-64.

[33]JIZG,MENDOZA C.Weakly non-linear stability analysis for dune formation[J].Journal of Hydraulic Engineering, 1997,123(11):979-985.

[34]ZHOU D C,MENDOZA.Growth model for sand wavelets [J].Journal of Hydraulic Engineering,2005,131(10): 866-876.

[35]FRANKLIN E M.Three-dimensional sand ripples as the product of vortex instability[J].Applied Mathematical Modeling,2012,37(5):3193-3199.

[36]白玉川,徐海珏.沙纹床面明渠层流稳定性特征的研究[J].中国科学E辑:工程科学材料科学,2005,35(1): 53-73.(BAIYuchuan,XU Haiyu.Stability characteristics of laminar flow over sand waves bed in open channel[J]. Science in China Ser E:Engineering&Materials Science, 2005,35(1):53-73.(in Chinese))

[37]COLOMBINI M,STOCCHINO A.Ripple and dune formation in rivers[J].Journalof Fluid Meahanism,2011, 673:121-131.

[38]ROUSSINOVA V,BALACHANDAR R,BISWAS N. Reynolds stress anisotropy in open-channel flow[J]. Journal of Hydraulic Engineering,2009,135(10):812-824.

[39]WANG Xianye,SUN Yi,LU Weizhen,et al.Experimental study of the effects of roughness on the flow structure in a gravel-bed channel usig particle image velocimetry[J]. Journal of Hydraulic Engineering,2011,16(9):710-716.

[40]赵程锦,邱秀云.底坡对人工渠道糙率影响的试验[J]水利水电科技进展,2013,33(6):48-51.(ZHAO Chengjin,QIU Xiuyun.Experimental study on effect of bottom slope on the artificial channel roughness[J]. Advances in Science and Technology ofWater Resources, 2013,33(6):48-51.(in Chinese))

[41]朱文谨,李瑞杰.感潮河段底床阻力特性分析[J].水利水电科技进展,2009,29(6):25-28.(ZHU Wenjin,LI Ruijie.Analysis on the riverbed resistance characteristic of tidal river[J].Advances in Science and Technology of Water Resources,2009,29(6):25-28.(in Chinese))

[42]HARD R J,BEST J L,LANE S N,et al.Coherent flow structures in a depth-limited flow over a gravel surface: The role of near-bed turbulence and influence of Reynolds number[J].Journal of Geophysical Research,2009,114 (1):3-21.

[43]NOGUCHIK,NEZU I,SANJOU M.Turbulence structureand fluid-particle interaction sediment-laden flows over developing sand dunes[J].Environmental Fluid Mechanics,2008,8(5/6):569-578.

[44]NEZU I,SANJOU M.PIV and PTV measurements in hydro-sciences with focus on turbulent open-channel flows [J].Journal of Hydro-Environment Research 2011,5(4): 215-230.

[45]OMIDYEGANEH M,PIOMELLIU.Large-eddy simulation of three-dimensional dunes in a steady,unidirectional flow:part 1.turbulence statistics[J].Journal of Fluid Mechanism,2013,721:454-483.

[46]LIU Shihe.Turbulent coherent structures in channels with sand waves[J].Journalof Hydraulic Dynamics,2002(2): 106-110.

[47]LÓPEZ F,FEMANDEZ R,BEST J.Turbulence and coherent flow structures associated with bedform amalgamation[J]Water Resources,2004(10):1-10.

[48]NEZU I,ADOTA A.Three-dimensional structure of space time correlation on coherent vortices generated behind dune crest.[J].Journal of Hydraulic Researches,1999, 37(1):945-958.

[49]CHANG K,CONSTANTINESCU G.Coherent structures in flow over two-dimensional dunes[J].Water Resources Research,2013,49(5):2446-2460.

[50]KESHAVARZI A,BALL J,NABAVI H.Frequency pattern of turbulent flow and sediment entrainment over ripples using image processing[J].Hydrology and Earth System Sciences,2012(16):147-156.

[51]GYR A,SCHMID A.Turbulent flows over smooth erodible sand beds in flumes[J].Journal of Hydraulic Research, 1998,36(6):1003-1007.

[52]DEY S,SARJAR S,SOLARI L.Near-bed turbulence characteristics at the entrainment threshold of sediment beds[J].Journal of Hydraulic Engineering,2011,137 (9):945-958.

Research development of the interaction between turbulence structure and bedforms in open channel

TANG Limo1,2,SUN Huidong2,LIU Quanshuai2(1.State Key Laboratory of Hydrology-Water Resources and Hydraulic Engineering,Hohai University,Nanjing 210098,China;2.College ofWater Conservancy and Hydropower Engineering, Hohai University,Nanjing 210098,China)

According to the latest researches at home and abroad,this paper summarized the research developments of the interaction between turbulent structure and bedforms,including research methods,turbulence characteristics in open channel flow,bedforms morphology influenced by turbulence,and turbulence characteristics influenced by bedforms.A greatmany achievements on the research of turbulence characteristics in open channel flow and characteristics ofwater flow and sedimentmotion over 2D bedforms have been obtained,yet the results cannot perfectly explain the sediment transport mechanism in natural rivers.Due to the limitation ofmeasurement technology,the research on interaction of turbulence and sedimentmovement under complex bedforms condition has not got obvious achievement for a long time.It is urgent to explore and introduce undisturbed and precise 3D flow measurement technologies.The geometrical morphology and evolution process of bedforms have been well known,while the mechanism of bedforms stability is controversial,neither theorymodels nor numericalmodels aremature enough,especially bedforms stability and sand movement characters under the combined action of interstitial flow and open channel flow are notwidely studied,which will be a research hot point in the future and become the basic of interaction mechanism between turbulence and sedimentmovement.

open channel;turbulence structure;turbulent characteristic;bedforms;bedforms evolution;review

TV143+.1

A

1006-7647(2015)02-0077-08

10.3880/j.issn.1006 7647.2015.02.016

2014-07-15 编辑:熊水斌)

国家自然科学基金(51479070,51125034)

唐立模(1977—),男,山东烟台人,副教授,博士,主要从事泥沙运动力学与河流动力学研究。E-mail:tanglimo@hhu.edu.cn