几何分布变异系数的贝叶斯估计

丁祖琴

(淮阴师范学院 数学科学学院, 江苏 淮安 223300)

几何分布变异系数的贝叶斯估计

丁祖琴

(淮阴师范学院 数学科学学院, 江苏 淮安 223300)

在熵损失函数下,研究了几何分布变异系数的贝叶斯估计问题,得到了变异系数的贝叶斯估计的一般形式和精确形式,并证明了它的可容许性.同时给出了变异系数的多层贝叶斯估计以及置信水平为1-α的贝叶斯置信区间.

几何分布; 变异系数; 熵损失函数; 贝叶斯估计; 置信区间

0 引言

几何分布是常见的离散分布之一,其统计特征及参数的估计和性质已得到广泛的研究[1-3].几何分布的变异系数也是应用统计学中一个常用的参数,在保险理论、可靠性以及医院统计等方面都有广泛的应用,但现代统计文献中对几何分布变异系数估计问题的理论研究却不多见.

本文讨论熵损失函数下几何分布变异系数的贝叶斯估计问题.在第一部分给出了几何分布变异系数熵损失函数的具体形式;第二部分给出了熵损失函数下对任何先验分布,几何分布变异系数的贝叶斯估计形式;第三部分给出了先验分布为指定分布时变异系数的贝叶斯估计的精确形式并证明其是容许估计;第四部分讨论了变异系数的多层贝叶斯估计的表达式;第五部分给出置信水平为1-α时参数的贝叶斯置信区间.

1 熵损失函数

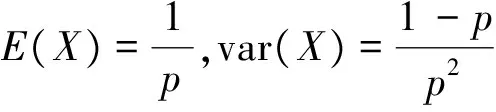
f(x1,x2,…,xn|p)=pn(1-p)T-n,

从而得到样本关于参数θ的联合概率函数为

f(x1,x2,…,xn|p)=(1-θ2)nθ2(T-n)

(1)

下面我们从样本X1,X2,…,Xn出发,在熵损失函数下求参数θ的估计.

θ的熵损失函数定义为[4]:

(2)

式(2)中,δ是θ的判决空间的一个估计.将参数θ的联合概率函数代入上述定义并化简整理可得

(3)

2 变异系数θ的贝叶斯估计

定理1 记X=(X1,X2,…,Xn),具有形如式(1)的联合分布,则在熵损失函数(3)下,对任何先验分布,几何分布变异系数θ的贝叶斯估计为

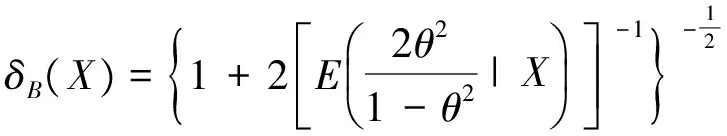
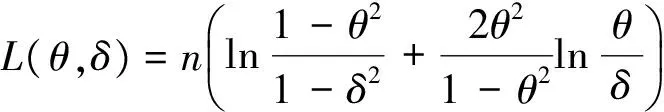
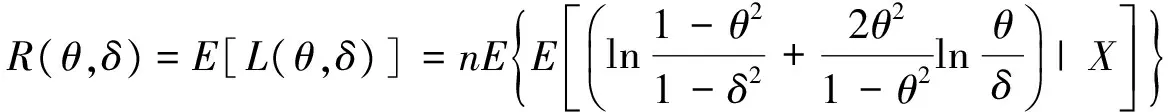
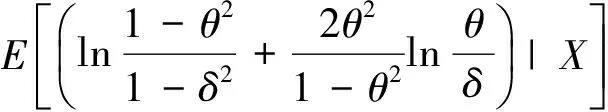
对h(δ)求导并令其为0,得

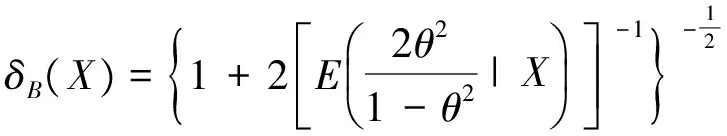
3 给定先验分布下,贝叶斯估计的具体形式

证明 由式(1)式及定理条件中给定的先验分布,得参数θ和样本X的联合分布为

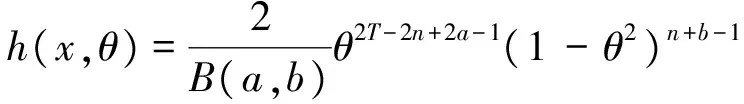
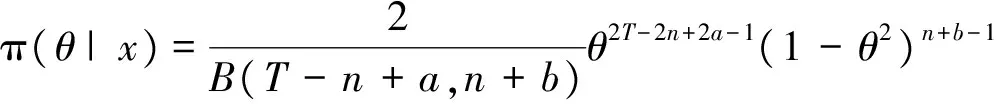
据此,可以计算

引理1[5]在给定的贝叶斯决策问题中,假如对给定的先验分布π(θ)的贝叶斯估计δB(X)是唯一的,则它是容许的.

证明 易证熵损失函数(3)关于δ是严凸的,从而贝叶斯估计δB(X)必唯一,再由引理1可得结论.

4 变异系数θ的多层贝叶斯估计

在理论上没有限制多层先验只分两步, 可以是三步或更多步, 但在实际应用中多于两步的先验是罕见的. 对第二步先验π2(λ), 用主观概率或用历史数据给出是有困难的, 因为超参数常常无法观察, 甚至连间接观察都难于进行. 这样用无信息先验作为第二步先验是一种好的策略, 但是必须满足试验结果的某些特性.

如果试验总次数n较大, 说明产品的可靠度大的可能性大, 所以选择p的先验分布应以增函数为宜[6].

取可靠度p的先验分布为Be(b,a)分布,a,b为超参数, 并设其独立. 由于只有在a<1且b>1时, 先验密度函数Be(b,a)关于p为增函数, 所以取a,b的超先验分布密度分别为均匀分布[7]

π2(a)=U(0,1),π2(b)=U(1,c),

c为常数,但是为了保证估计的稳健性,c不宜过大.

定理4 对几何分布G(p),在给定上述两层先验分布和熵损失函数(3)下,θ的两层贝叶斯估计为

证明 由上述两层先验分布可知,θ的先验分布为

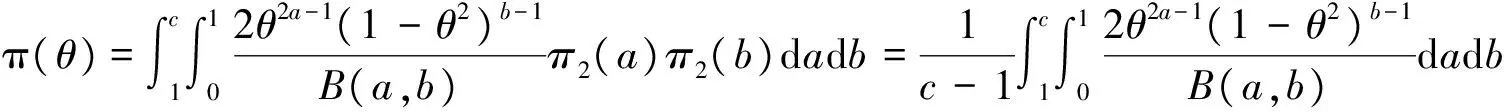
故参数θ和样本X的联合分布为

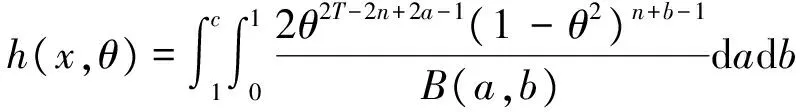
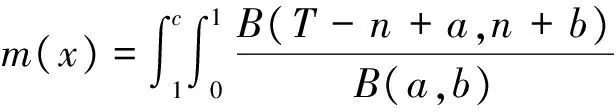
进一步可求得

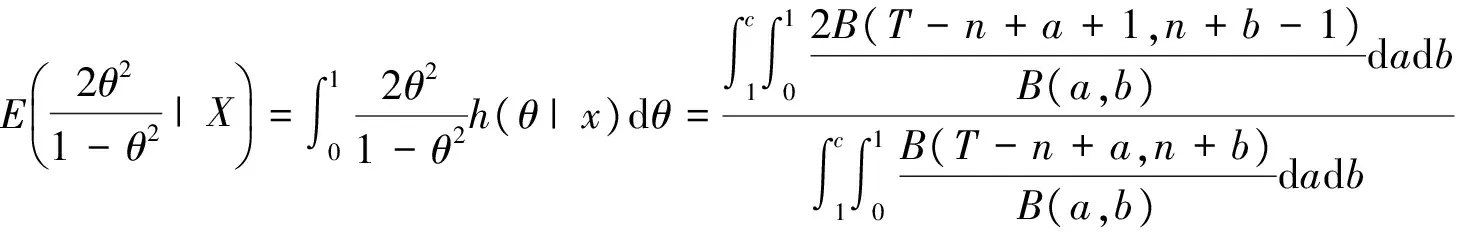
从而得熵损失下θ的两层贝叶斯估计为

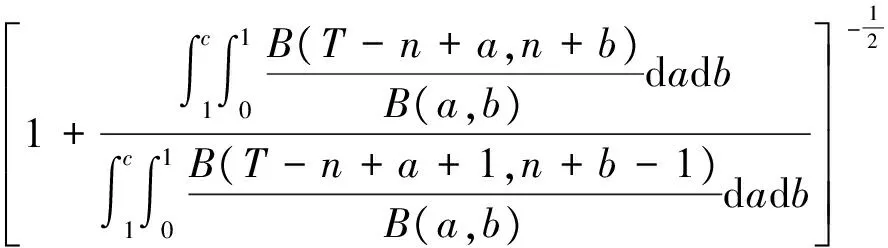
5 θ的置信水平为1-α的贝叶斯置信区间

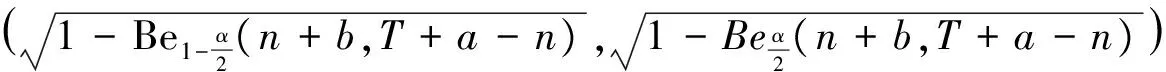
证明 由于θ的先验分布为

则几何分布可靠度p=1-θ2的先验分布为

其中a>0,b>0,即为贝塔分布Be(b,a),从而p的后验为

h(p|x)∝pn+b-1(1-p)T+a-n-1,

即为Be(n+b,T+a-n).对给定α∈(0,1),有

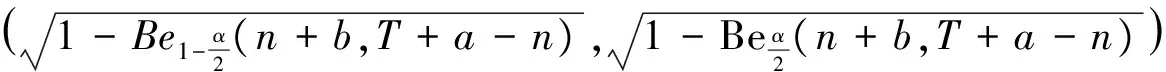
[1] 徐晓玲,王蓉华,费鹤良.几何分布的几个性质[J].数学研究,2008,41(1):103-112.

[2] 赵喜林.几何分布可靠度的截尾Bayes估计[J].武汉科技大学学报:自然科学版,2004,27(1):93-95.

[3] 韩明,崔玉萍.几何分布可靠度的估计[J].运筹与管理,2001,10(4):35-38.

[4] 王德辉,赖民,宋立新.熵损失函数下Poisson分布参数倒数的Bayes估计[J].吉林大学:自然科学学报,2000(4):17-22.

[5] 茆诗松,王静龙.高等数理统计[M].北京:高等教育出版社,1998:367-372.

[6] 韩明. 多层先验分布的构造及其应用[J].运筹与管理, 1997(6):31-40.

[7] 王德辉,牛晓宁. 熵损失函数下巴斯卡分布参数的Bayes估计[J].吉林大学:自然科学学报, 2001(1):19-22.

[责任编辑：李春红]

Bayesian Estimation of Geometric Distribution Variation Coefficient

DING Zu-qing

(School of Mathematical Sciences, Huaiyin Normal University, Huaian Jiangsu 223300, China)

This paper studies the Bayesian estimation problem of geometricdistribution variation coefficient under entropy loss function, obtains thegeneral form and precise form of Bayesian estimation of variation coefficient,and proves its admissibility. Then the paper gives multilayer Bayesianestimation of variation coefficient and Bayesian confidence interval with confidence level1-α.

geometric distribution; variation coefficient; entropy loss function; bayesian estimation; confidence interval

2015-06-07

丁祖琴(1977-),女,江苏淮安人,讲师,硕士,研究方向为数理统计. E-mail: freedingd@163.com

O212.8

A

1671-6876(2015)04-0291-04