基于科学实验室系统的受迫振动特性研究

邢 起 曲连晔 倪 晨 方 恺 何雨华 郭先红

（同济大学物理科学与工程学院，上海 200092）

受迫振动是一种在自然界普遍存在的物理现象，用波尔共振仪研究受迫振动特性是研究受迫振动的典型例子之一，有助于增强对振动的理解.传统的实验方法通过测量波尔共振仪的振幅和周期得到阻尼系数、幅频特性和相频特性曲线，无法实现对摆轮实时运动状态的描述，不利于直观全面掌握运动的物理规律[1，2].本文在传统实验方法的基础上，利用转动传感器和PASCO平台对摆轮的运动特性进行了全面分析，不仅得出阻尼系数β的值以及幅频和相频特性曲线，而且通过实时测量直观地展示了摆轮的运动状态，提高了实验精度.实验采用Science Workshop 750Interface接收数据、转动传感器CI-6538和多功能的数据处理软件Datastudio，实现了对波尔共振实验的自由振动、阻尼振动及受迫振动的分析.

1 PASCO系统简介

PASCO系统由美国PASCO公司开发研制，利用传感技术将非电学量转换为电学量，通过计算机实现高效、准确采集，并将实验的数据图表实时地显示，准确形象地展示各物理量的变化规律.在物理实验方面，设备涵盖了力、热、光、电、机械波及原子物理等上百个实验.其通用的数据采集系统 “科学工作室”（Science Workshop），是一种应用于科学实验的数据收集系统.“科学工作室”主要由3部分组成：计算机接口、传感器和软件.PASCO系统是采用传感器和数据采集器接口，通过Datastudio操作平台进行控制和数据采集的物理实验系统.用PASCO的Since Workshop系统设计实验，实验系统如图1所示[3-5].

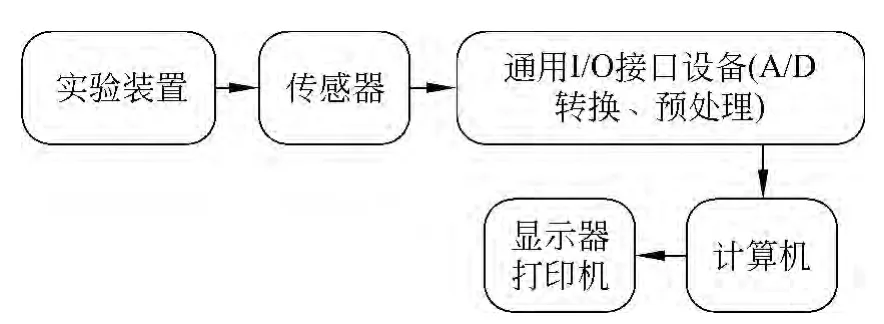
图1 PASCO实验系统原理框图

2 实验原理

在受迫振动状态下，系统除了受到策动力的作用外，同时还受到回复力和阻尼力的作用.所以在达到受迫振动的稳定状态时，物体的位移、速度变化与策动力变化不是同相位的，而是存在一个相位差.在无阻尼的条件下当策动力频率与系统的固有频率相同时产生共振，振幅最大，相位差为90°.

波尔共振仪实验采用摆轮在电磁阻尼力矩作用下作阻尼振动，在外加驱动力作用下做受迫振动的方法，来研究受迫振动特性，可直观地显示机械振动中的一些物理现象.当摆轮受到周期性策动力矩M＝M0cosωt的作用，并在有空气阻尼和电磁阻尼的媒质中运动时（阻尼力矩为-β·（dθ／dt）），其运动方程为

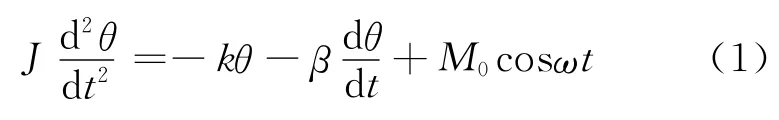
式中，J为摆轮的转动惯量，-kθ为弹性力矩，Μ0为强迫力矩的幅值，ω为强迫力的圆频率，β为阻尼系数.

式（1）的通解为

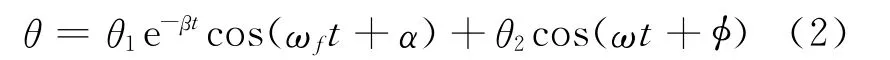
由式（2）可见，受迫振动可分成两部分：

第一部分，θ1e-βtcos（ωft＋α）与初始位置有关，经过一定时间后衰减消失.

第二部分，说明强迫力矩对摆轮做功，向振动体传送能量，最后达到一个稳定的振动状态.

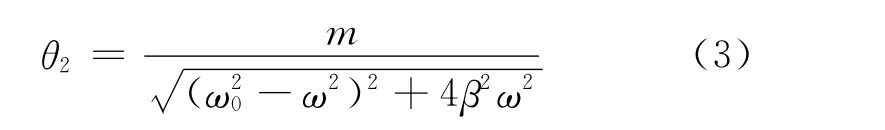
它与强迫力矩之间的相位差为

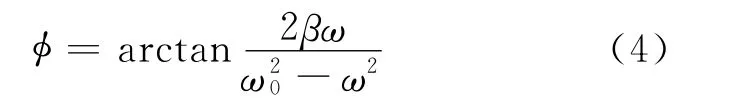
由式（3）和式（4）可看出，振幅θ2与相位差φ的数值取决于强迫力矩M、频率ω、系统的固有频率ω0和阻尼系数β，而与振动初始状态无关.

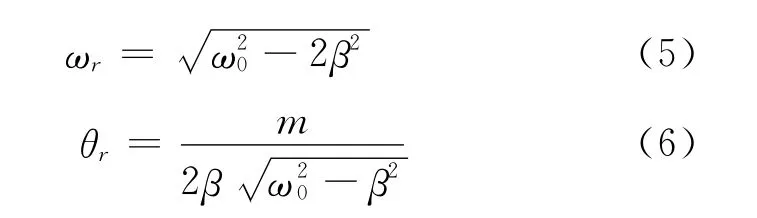
式（5）和式（6）表明，阻尼系数β越小，共振时圆频率越接近固有频率，振幅θr也越大，图2和图3表示在不同β时受迫振动的幅频特性和相频特性[6].

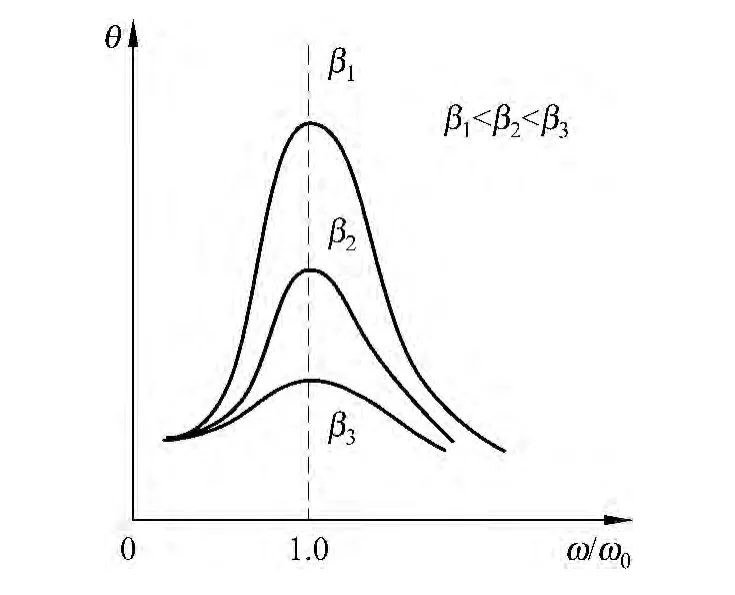
图2 幅频特性

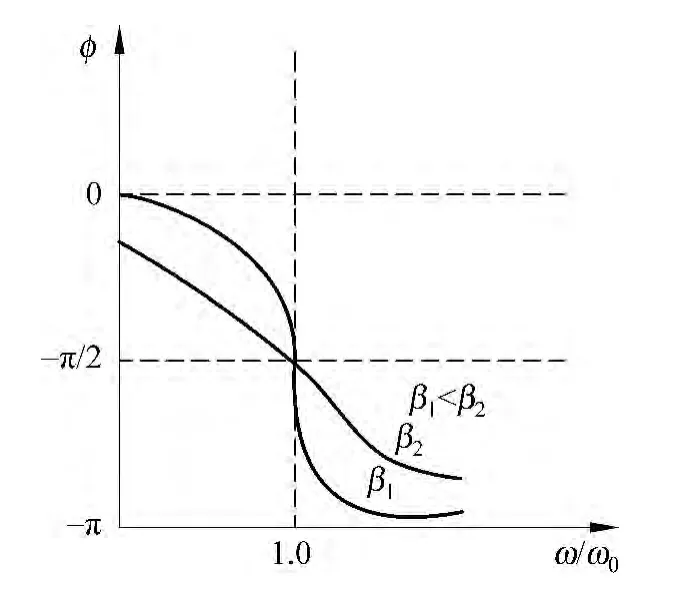
图3 相频特性

3 实验装置

传统实验一般采用光电门测定波尔共振仪的振幅和周期，为了获得提供策动力的电机及摆轮的实时运动状态，我们利用两个转动传感器分别测量其角位移随时间的变化过程，并通过Datastudio软件进行数据拟合得到其振幅和周期.

为确保摆轮与转动传感器运动同步，我们分别采用滑轮及轻触连接的方法将两个转动传感器与摆轮及电机转盘相连接.实验装置如图4所示.细线一端固定连接到摆轮上，另一端连一个5g的砝码自然下垂，中间缠绕在转动传感器的滑轮上，以此测量摆轮的运动状态.电机运动状态的测量，通过与另一转动传感器的滑轮直接轻触连接实现.

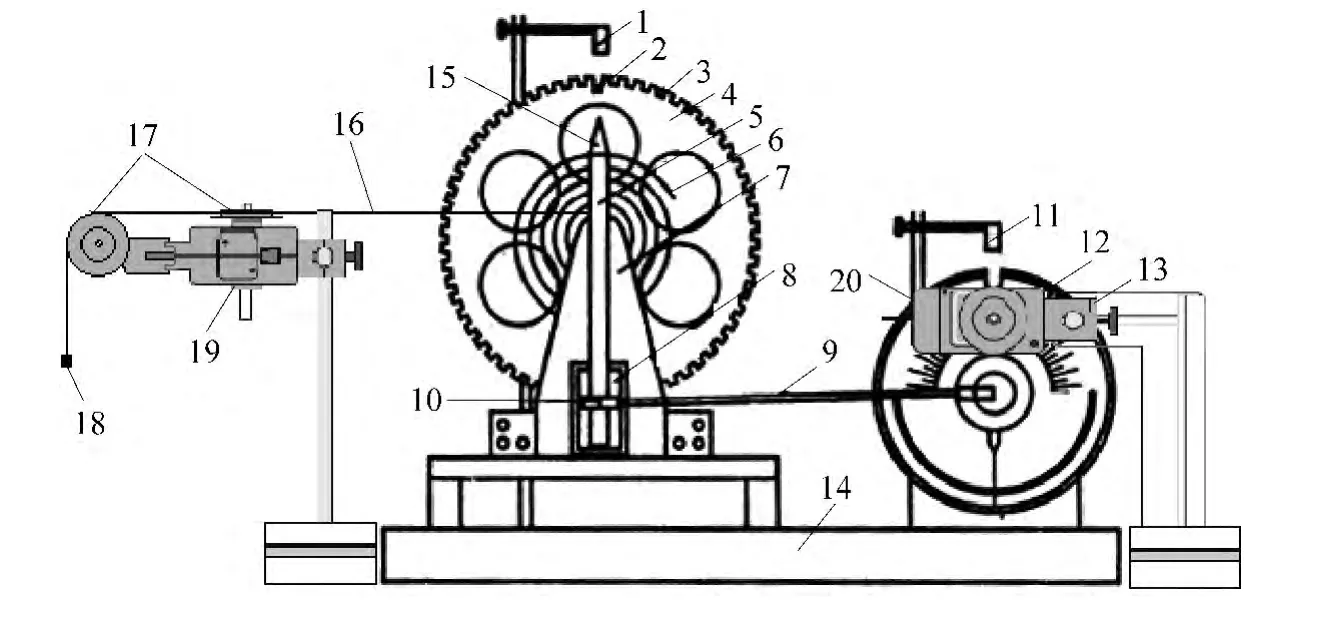
图4 实验装置图

实验装置水平放置，转动传感器1测量摆轮的运动状态，转动传感器2测量电机运动状态，将两传感器连接到Science Workshop750接口上，并将其连接到计算机.

4 实验过程与数据分析处理

4.1 阻尼系数β的测定

设置摆轮初始转过的角度为150°，采用PASCO系统，在Datastudio软件中记录下振动角度的实时数据点.横轴为时间，纵轴为摆轮转过的角度.显然，摆轮在做周期性衰减振动.

我们将数据点导入到Origin软件中，作出图像，并对图像进行曲线拟合，

图5（a）为关闭电磁阻尼开关，自由释放摆轮情况下的振幅随时间变化曲线，图5（b）、图5（c）和图5（d）分别为仪器所设定的电磁阻尼“1”、“2”、“3”挡下的振幅随时间变化曲线.

图5（a）情况下小阻尼振动方程为

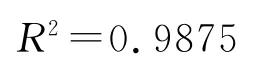
由振动解析式可知，自由振动条件下的阻尼系数为0.01162，周期为2π／3.9904＝1.5746s.

由于空气阻尼以及轴承摩擦等阻尼的存在，自由振动下系统振动也会有略微的衰减.在振动后期，函数图像拟合偏离实验值较大，实际振动的衰减相比拟合出的曲线更为强烈，周期也略大，可以看出弹簧的非线性效应以及轴承的摩擦存在对结果有一定的影响[7].

对于电磁阻尼1、2、3挡下，我们采用同样的数据拟合方法，分别得到它们的振幅时间图、曲线拟合图像以及拟合函数.经拟合得各阻尼挡下阻尼系数β如表1所示.

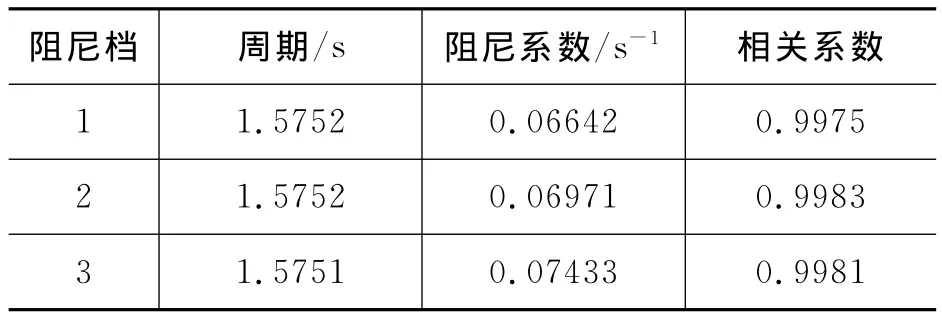
表1 各电磁阻尼挡下的阻尼系数β值

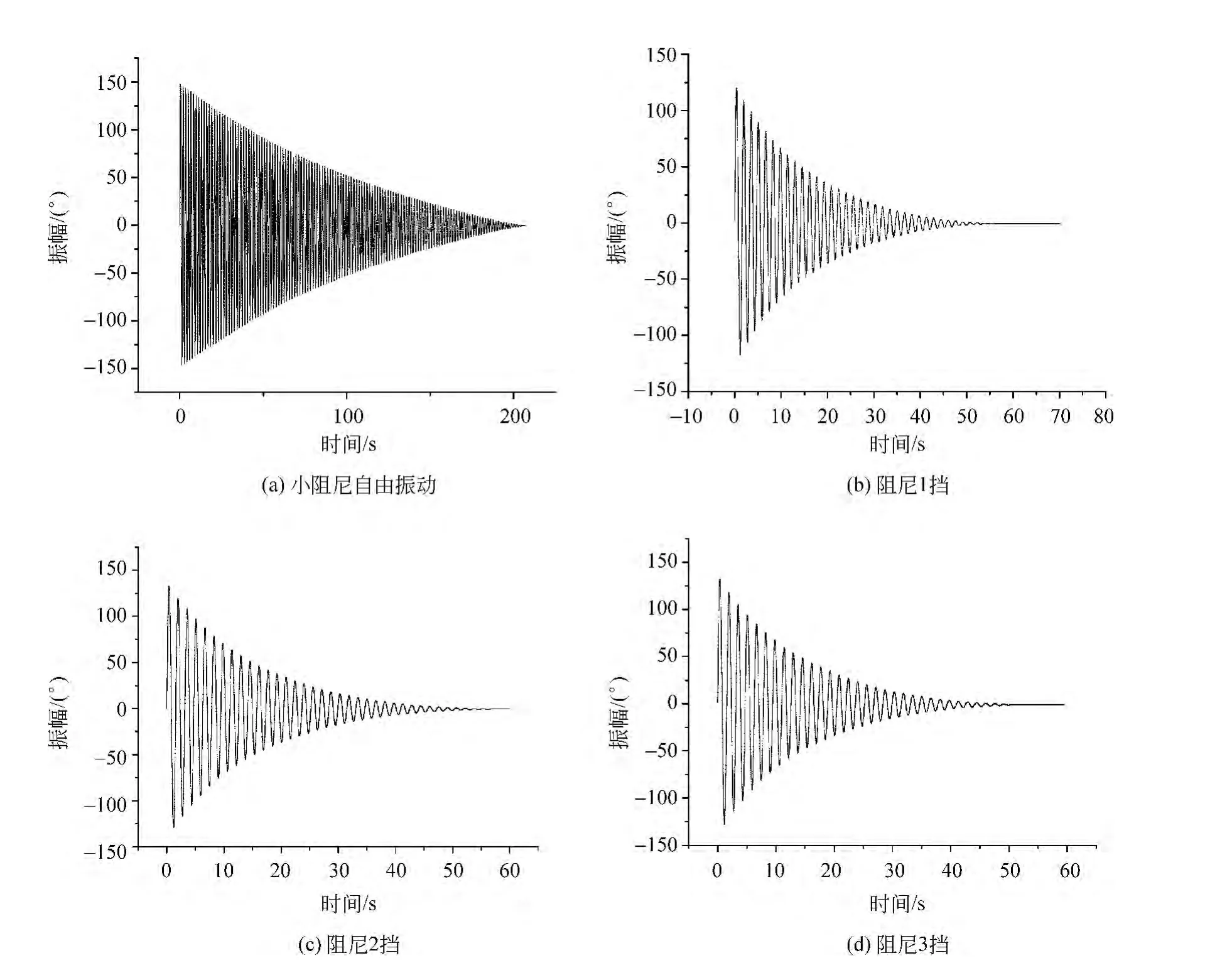
图5 阻尼振动条件下摆轮的振幅随时间变化曲线

相比于关闭电磁阻尼开关小阻尼时，阻尼增大后，阻尼系数明显增大，周期也有小幅度增加.

4.2 摆轮的幅频特性与相频特性

1）幅频特性

在实时测量法中，对于系统稳定时的振幅，可以从实时测量记录的数据点中得到.在Datastudio软件中，我们选取最终系统稳定时的足够数据点，并对这些点进行正弦曲线拟合，得到正弦函数，从函数表达式中可以直接读出系统稳定振动时的振幅和周期，如图6情况下摆轮的最终振幅为60.9°，周期T为1.52s.

利用上面的方法，改变电机转速，分别测量摆轮振幅和周期的变化.在阻尼1挡下，摆轮振幅随电机转速变化的数据，利用Origin绘制幅频特性曲线，如图7所示.

2）相频特性

在以上的测量过程中，若分别以策动力振幅和摆轮振幅为坐标系的横纵轴作图，形成稳定的李萨如图（见图8），则可计算摆轮与电机的相位差.

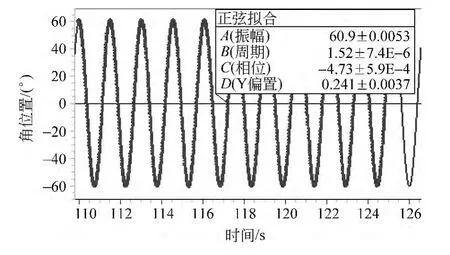
图6 摆轮振幅实时测量图表

阻尼1档下，电机驱动周期为1.5251s时得到的李萨如图，此时二者的相位差162.5°.用同样的方法，可测得电机不同驱动频率下的相位差.利用Origin绘制幅频特性曲线，如图9所示.

综上所述，利用PASCO系统对摆轮与电机的振动角位移进行实时测量，可得到摆轮位移共振下的幅频特性曲线与相频特性曲线，实验结果与符合位移共振理论模型.

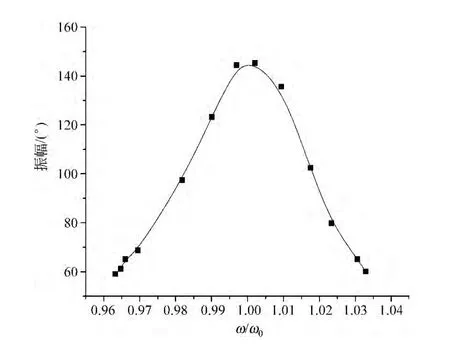
图7 幅频特性曲线

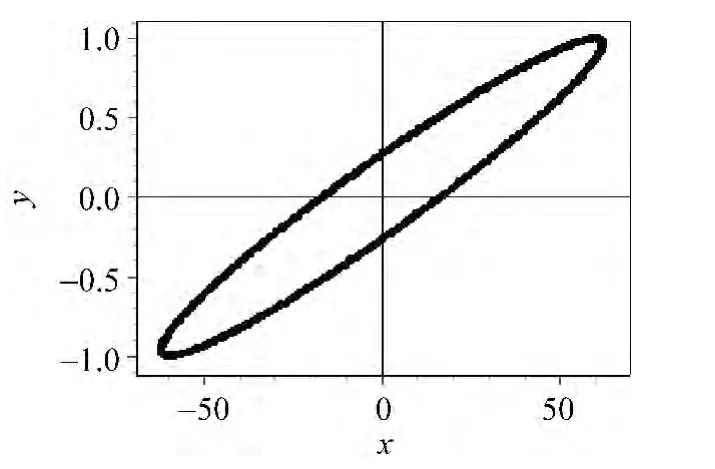
图8 摆轮和电机振动形成的李萨如图

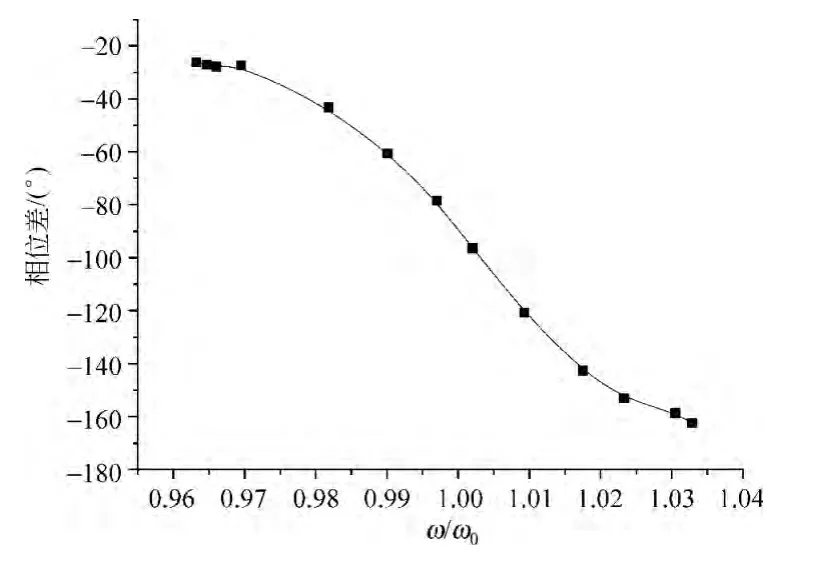
图9 相频特性曲线

4.3 观察分析受迫振动的耦合图像

在受迫振动中，我们利用PASCO系统实时测量，记录下整个振动过程.在实验中，我们将摆轮从开始被电机带动振动，经历耦合，到最终与电机一起稳定振动的图像，通过Datastudio软件记录下来，整个振动过程如下：

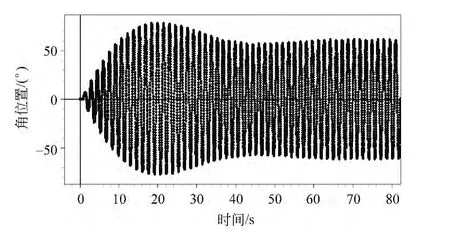
图10 摆轮振动的全过程图

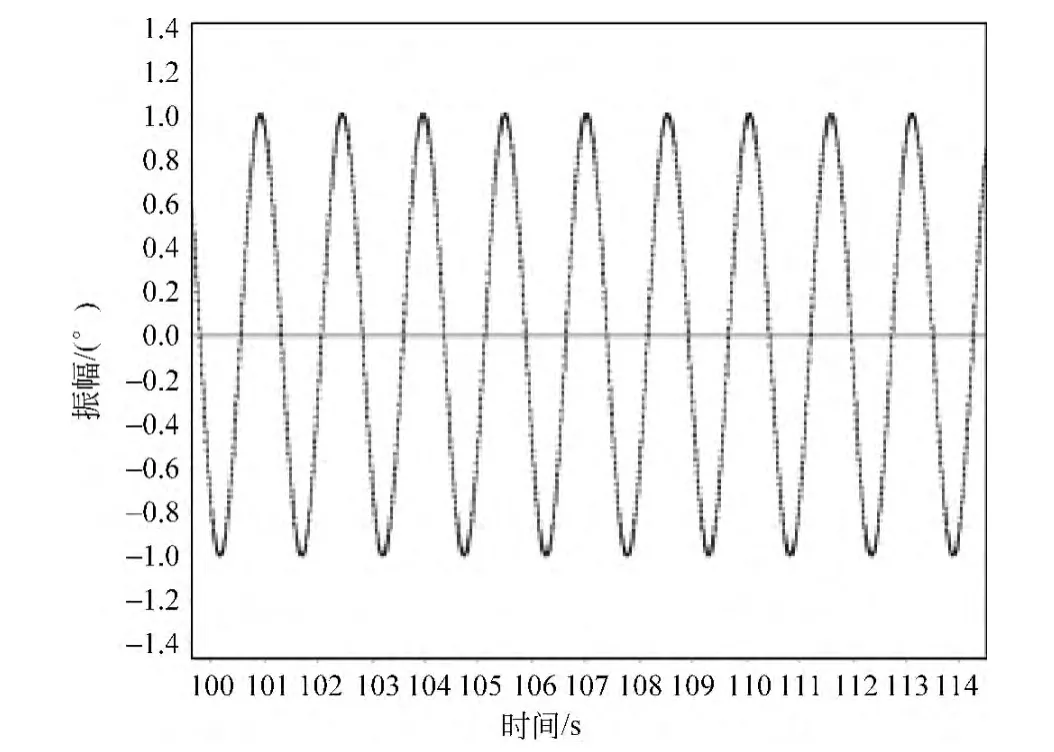
图11 电机稳定振动

观察图形发现，在达到共振前，摆轮的振动出现了类似耦合摆中“拍”的现象（图10），摆轮的运动是自身振动和电机带动（图11）两个谐振动合成的“拍”，振幅时大时小有节奏地变化.达到稳定振动的标志就是振幅最大且不再随时间变化（图12），此时摆轮周期与电机周期相同.在式（2）中提到，受迫振动可分成两部分：第一部分，θ1e-βtcos（ωft＋α）与初始位置有关，经过一定时间后衰减消失.摆轮振动过程中，前期不稳定的“拍”的现象也就是公式中第一项衰减的过程，最后达到的稳定状态，也就是第二部分，强迫力矩对摆轮做功，向振动体传送能量，最后达到的稳定振动状态.

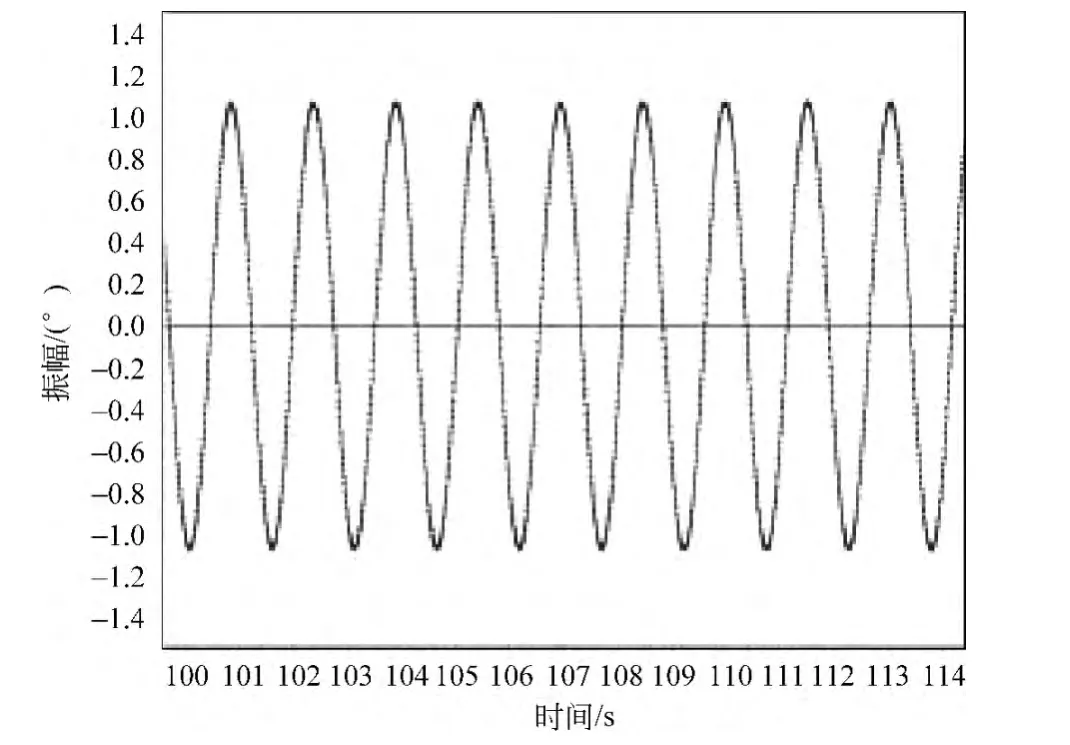
图12 摆轮稳定振动

4.4 误差分析

在对实验仪器的改装中，增加了传感器以及测量摆轮的传感器的连接中采用了细线悬挂重物带动滑轮转动的方式，因此会导致摆轮的转动惯量J增加，由ω20＝k／J可知，其ω0偏大，因此在整个实验中我们得到的周期值T偏小.若采用无触点的角度传感器，则可减小因此而产生的系统误差[8].另外，通常理论分析认为弹簧的弹性系数k为常数，实际当摆轮的振幅较大时，弹簧超出弹性限度，对实验结果造成影响.此外仪器的系统误差也会造成一定的影响，尤其是在传感器的连接时，策动力电机的转动半径与传感器的不同，测量直径时无法避免产生系统误差，导致半径比不准确.因此会导致相位差不能长时间保持稳定.

5 结语

基于PASCO实验测量平台，不仅可实时观测摆轮在自由振动、弱阻尼振动及受迫振动状态下的运动图像，使实验过程更直观且易于理解.还可通过Datastudio软件或Origin等数据处理软件，对数据进行计算分析，使实验结果更为准确.通过观测受迫振动中摆轮的完整运动过程，有助于理解受迫振动的物理现象的本质，拓展原有的大学物理实验教学内容和测量方法，深入掌握其物理规律.

[1]陆廷济，胡德敬，陈铭南.物理实验教程[M].上海：同济大学出版社，2000：66-72.

[2]方恺，等.物理实验学习册[M].上海：同济大学出版社，2011：49-56.

[3]兆雪.浅谈PASCO设备的管理[J].延安职业技术学院学报，2010（10）：66-67.

[4]陈竹.探索实验室——美国PASCO整体解决方案[J].中国教育技术装备，2005（4）：53-56.

[5]林淑淇，等.基于PASCO系统的简谐运动特性研究[J].物理通报，2014（2）：83-86.

[6]朱华泽.用波尔共振仪研究受迫振动特性[J].大学物理实验，2011（6）：57-60.

[7]董霖，等.波尔共振实验“异常现象”的研究[J].大学物理，2010（2）：57-60.

[8]程敏熙，等.周期性外力驱动的混沌摆[J].物理实验，2009（1）：7-13.