信息化舰炮武器动态精度试验样本量及标准差算法
王立红,武瀚文
(解放军92941 部队,辽宁葫芦岛 125001)
舰炮武器是体系对抗及联合打击中不可或缺的“火力元”,是火力无缝联接中的“神经元”。以信息化弹药为特征的信息化舰炮武器系统具有开放式体系结构,与传统大中口径舰炮武器系统相比,时序更加复杂化、主配弹种、打击范围和作战能力以及试验鉴定的方法和手段等方面均存在很大差别。动态精度是舰炮武器系统的一项重要指标,动态精度试验的样本量与估计的精确度、置信度、试验质量和试验消耗密切相关;信息化弹药相对昂贵,所以信息化舰炮武器动态精度试验样本量设计是靶场试验面临的新课题,直接关系到产品质量和试验消耗。如果试验样本量选择不合理造成子样数太多,会造成试验消耗过大;如果真值精度低、子样数不够则难以保证评估精度。
1 点估计与样本量
舰炮武器系统的多项技术指标是服从正态分布的随机变量,即使有些非正态分布随机变量,只要采集样本量足够大,母体也渐近于正态分布,对这些随机变量采用点估计是常用的主要方法。假设X1,X2,…,Xn,是由试验总体X∈N(μ,σ2)中观测的一组样本,其中总体参数μ 和σ2是未知的。如果试验观测是独立的,那么,总体参数μ 和σ 就可以用样本平均值和样本标准偏差Sx来进行估计。和Sx就称为总体参数μ 和σ 的点估计。点估计是对总体参数的最佳单值预测,当估计量的数学期望等于被估参数时,称为无偏估计,否则称为有偏估计。
样本均值

样本标准差

修正的样本标准差

样本的r 阶原点矩

样本的r 阶原点矩

其中:Sx为样本标准差,通常用于子样数大于30 ~50 时为修正的样本标准差,通常用于子样数小于30 的情况下;为样本方差; 在舰炮武器试验中通常用来统计系统精度,
运用统计分析方法,必须要有一定的样本量,才能保证对参数估值的估计精度。通常样本量越大,估计精度就越高。但是对于信息化舰炮武器系统试验,信息化弹药等费用昂贵造成试验消耗较大,所以不可能进行大量的试验次数。所以工程实践中要按小子样情况处理[1-2]。
2 约束测量条件下试验样本量
2.1 动态精度指标及试验测量要求
动态精度指标的含义是:在典型目标按典型规律运动条件下,武器系统安装在舰艇上、按战斗方式工作时,炮口的指向误差。一般采用系统误差与随机误差来描述[3]。
在动态精度试验中,真值参数主要包括目标相对于跟踪传感回转中心的距离、方位角、高低角,目标运动参数等,一般真值测量设备的采样频率与录取系统的采样频率相同,而且至少要保证在误差相关时间内有一定的采样。真值测量设备可以用光测设备、雷达、GPS 等多种手段[4];武器平台的纵摇角及横摇角瞬时值真值,其精度一般要比被试武器系统参数的精度高一个数量级,以满足武器系统及相关单机的试验要求。根据误差测量理论[5-6],靶场真值参数精度与相应的被试参数精度的关系必须满足“1/3”和“1/10”法则。当X0的精度满足式(6)、式(7)时,X0的误差ΔX0可以忽略不计。

式中:X、X0分别为被试参数和真值参数; ΔX0、ΔX 分别为真值参数误差和被试参数误差;E(ΔX0)、E(ΔX)分别为真值参数误差均值和被试参数误差均值。
2.2 样本量算法
随机变量x 服从正态分布,即x ~N(μ,σ)。通过试验获得一个容量为n 的子样,子样均值子样标准差Sx。由于采样的随机性,统计量仍为随机变量。假设误差序列为X=x1,x2,…,xn,当子样数n 为有限时,误差均值的点估值为

Sx均方差为


靶场试验中,样本均值的均方差与样本标准偏差之比称为相对精度θ,假设样本标准偏差估计的置信概率取0.683,相对精度θ 取0.1。用、Sx作为母体特征量μ、σ 的估值,要相对足够小,即:

为使式(12)、式(13)同时成立,n≥100,则样本量n =100。通常动态精度试验中靶场最关心的样本量为有效航次,而根据求得的样本量和独立采样数可以确定有效航次。假设独立采样数为10 次,则可以初步确定有效航次为10个; 如果采样数15 次,则有效航次为7。
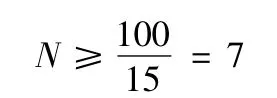
2.3 样本标准差算法
在常规舰炮武器试验中通常使用修正的样本标准差Sx来进行误差的统计分析。但对于小子样,Sx并不是一个很好的估值,中西方相关文献[7]均已提及要进行均方根统计修正。所以对于信息化舰炮武器应使用有偏估计的样本标准差


式中a 取值如表1 所示。

表1 α 参考值表
3 等精度测量条件下试验样本量
随着计算机及网络通信等高新技术的不断发展及在武器系统中的应用,武器系统的精度与靶场真值测量设备精度的差距越来越小,特别是在仿真试验中,有时会达到了同一数量级甚至等精度,严格按照“1/3”和“1/10”法则,在这种条件下测量的参数是无效的。所以,靶场测控装备的保障要求将大大提高,文献[8 -9]表明通过选择增大样本量可以补偿精度的不足。下面首先将等精度测量分为测量误差为零和存在测量误差两种情况,然后分别对其样本标准差精度计算公式进行推导,进而求出等精度条件下的试验样本量。
3.1 推导样本标准差精度
假设测量随机误差为ξ(ξ1,ξ2,ξ3,…),被试品进行了n次试验,被试品真实精度为测量设备固有精度
1)测量误差为零
当测量误差等于零时,观测结果X(X1,X2,…,Xn),设S″x的精度为D(S″x),从式(14)入手,则:

又因为

所以:

2)测量误差不为零
当测量误差不等于零时,观测结果Y(Y1,Y2,…,Ynξ),为测量误差不等于零时为抵消影响所进行的试验次数,同理可知
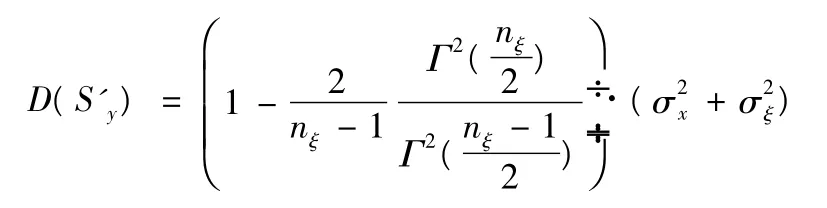
3.2 求取等精度测量试验样本量
在等精度测量条件下,欲求取试验样本量,需要满足

则将有以下关系式

运用图解法及插值等进行大量计算[9]可得

即在等精度测量条件下,若使方差估值精度维持在相同水平上,试验次数应该大于精度鉴定指标,近似取2 倍。该方法的实质是以增大试验次数来补偿测量误差的不利影响,使有无测量误差情况下,两者估值精度维持在相同水平。
4 仿真验证
在实际工作中,首先将模拟的航路参数注入某仿真测试系统,在“1/3”和“1/10”法则约束测量条件下选择子样数为n,在等精度测量条件下选择子样数为2n,驱动仿真测试系统运行,两种条件下仿真测试结果均满足工程实践要求。等精度条件下的仿真算例如下。
4.1 模拟航路参数
1)模拟岸上目标航路
初始距离为2 km,方位角为350°,高低角为1.2°,高度为40 m;模拟舰艇参数:速度为30 kn,航向为30°;横摇幅值为15°,横摇周期为12 s;纵摇幅值25°,纵摇周期为10 s。
2)模拟空中目标航路
初始距离为20 km,航向为240°,方位角为60°,高低角为1.432°,速度为680 m/s,高度为500 m;模拟舰艇参数:速度为30 kn,航向为30°;横摇幅值为10°,横摇周期为8 s;纵摇幅值15°,纵摇周期:10 s。
3)模拟海上目标航路
初始距离为3 km,航向为255°,方位角为70°,高低角为0°,速度为10 m/s,高度为0 m;模拟舰艇参数为速度30 kn,航向为30°;横摇幅值为7°,横摇周期为10 s;纵摇幅值11°,纵摇周期为10 s。
4.2 模拟测试
按照4.1 模拟岸上、空中和海上3 类目标航路参数,分别注入某仿真测试系统中,并将该系统的理论值计算精度与被试系统精度设置为同一数量级,模拟有效航次数设定为2n,在此条件下驱动系统运行,系统工作正常,仿真测量结果如表2 所示,岸上目标动态精度仿真测试误差曲线如图1 所示。对精度测量结果及误差曲线分析表明:等精度条件下,在模拟试验中应用此样本量算法可以满足要求。

表2 仿真测试结果

图1 岸上目标误差曲线
5 结论
本研究从靶场试验设计的角度,针对信息化舰炮武器的特点,提出了在等精度测量及“1/3”和“1/10”法则约束条件下的试验样本量算法,并在模拟试验中进行仿真验证。因此,在信息化舰炮武器试验中,在保证精度评估置信度的前提下,如果测控设备精度足够高,可以改进样本量算法来减少子样数,达到节省试验经费、降低试验消耗的目的;如果测控设备精度不够高,那么可以适情通过增大样本量来弥补精度的不足,特别是在仿真试验中,该方法可行有效。
[1]孙锦,李国林,许诚.小子样条件下导弹靶场试验综合评定方法[J].火力与指挥控制,2014,39(9):179-180.
[2]段中岳.反导武器系统小子样试验鉴定技术研究[D].长沙:国防科学技术大学,2007.
[3]夏小华,刘奎永,冯元伟.舰炮武器试验中目标坐标真值修正方法[J].指挥控制与仿真,2012,34(6):134-136.
[4]姚飞娟,王建强,杜娟,等.精度鉴定试验中GPS 测姿方法及测姿精度分析[J].电子测量技术,2013,36(8):49-50.
[5]武小悦,刘琦.装备试验与评价[M].北京:国防工业出版社,2008:256-299.
[6]邢昌风,李敏勇,吴玲.舰载武器系统效能分析[M].北京:国防工业出版社,2008:12-14.
[7]周淦林.小子样下均方根统计的修正问题[J].海上试验靶场,1991(6):2-5.
[8]周淦林.关于测量设备与被试品处于等精度条件下的试验设计问题[R].出版地不详:[出版社不详],2009.
[9]朱绍强,李相民.舰炮武器系统仿真试验可信性评估方法[J].火力与指挥控制,2014,39(10):36-40.
[10]钱贵鑫,由大德,李进军,等. 舰炮作战训练数据录入与分析系统总体框架设计[J].兵工自动化,2014(12):32-34.

