飞机对水下目标探测干扰磁场模型化补偿算法

焦安龙，张 宁，庞学亮

(1. 91439 部队460 所，辽宁大连 116041;2.海军工程大学兵器工程系，武汉 430033)

在飞机材料和结构形状确定的条件下，飞机干扰磁场与飞行姿态、航速、航行地区的磁场矢量密切相关，飞机干扰磁场包括飞机的剩磁场、磁化磁场和涡流磁场等3 部分［1］。飞机直航时，飞机背景磁场可分为恒定成分和变化成分，其中恒定成分的大小一般在10 ～100 nT 范围内，变化成分的大小为几nT 量级，和地磁测量的应用背景有区别，以精确磁探为目标的磁探仪，要重点关注对干扰磁场变化成分的补偿。当对飞机背景磁场的补偿效果达到90%时，补偿后飞机背景磁场干扰的变化成分将降到0.1 nT 以下，可以保证较远距离磁性目标的有效探测。

Tolles-Lawson 方程是被广泛应用的飞机磁场模型，本文考虑地磁总强度的变化对涡流场的影响，对飞机Tolles-Lawson 模型进行改进，并从方向余弦获取以及模型参数估计方面对补偿算法进行设计。最后的算法数据仿真表明，本文算法能有效的补偿飞机磁场干扰，显著的提高对远场弱磁信号的探测能力。

1 飞机背景磁场建模及模型改进

飞机剩余磁场、感应磁场和涡流磁场矢量分别用Hp、Hi、Hw表示。建立飞机磁场模型坐标系，磁探设备探头以拉杆式悬于飞机尾部，以磁探头为坐标中心，X 轴与飞机纵轴平行，向前为正;Y 轴与飞机横轴平行，向右为正;Z 轴与飞机的垂直轴平行，向下为正，如图1 所示。

地磁场矢量H0的方向由地磁场与X，Y，Z 轴形成的方向角θi0= (X0，Y0，Z0)决定，其方向余弦为(cosX0，cosY0，cosZ0)。

图1 飞机磁场建模坐标系

Tolles-Lawson 方程建立的涡流磁场模型中，都是假设地磁场恒定不变，没有考虑上式右边的最后一项，表示的是由于地磁场总强度变化引起的涡流磁场，在高精度目标磁场测量中这一项是必须考虑的，特别对于飞机地磁变化率相对较大，这一项更需要考虑。所以模型的求解就是利用测量数据求解式(5)线性方程中的17 个未知系数。

恒定磁场可以视为短时间稳定不变，表示为

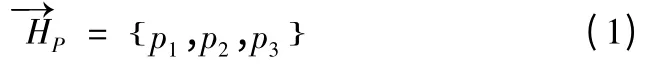
感应磁场各分量与地磁场在飞机的各个轴上的投影成正比，定义感应矩阵K，则感应磁场可表示为下式［2，3］

一个课时很难完成所有教学任务，因此教师可在课前录制微视频（如摄像软件的使用和spss软件使用方法）来提高上课效率。另外，教师也可通过培训兴趣小组，让兴趣小组成员在上课期间充当每组的“小组长”来帮助带动其他同学更快完成本节实验拓展课的教学任务。

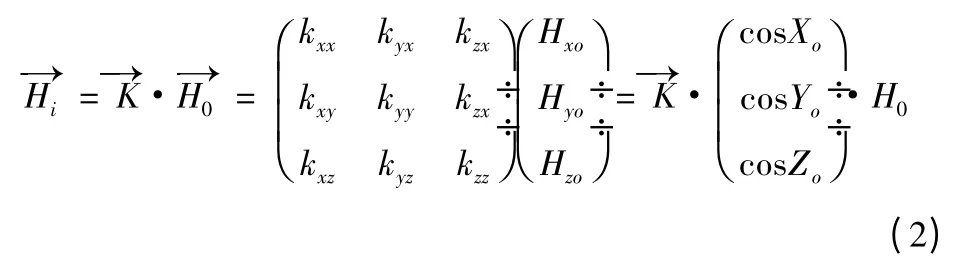
而涡流磁场与投影到各坐标轴磁场的变化率成正比，定义涡流矩阵，则涡流磁场可表示为下式

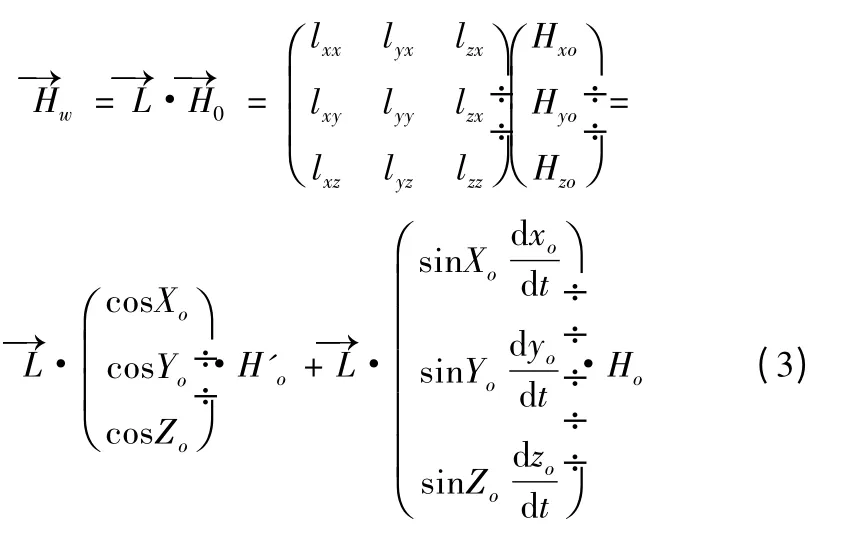
则光泵磁探仪测得的总磁场即为

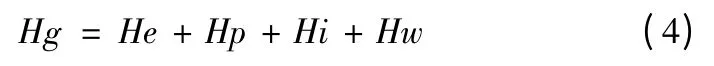
Hg为测量的总磁场，包括地磁场He 和干扰磁场。由于地磁场的变化率较小，利用高通滤波器，就可以从测量数据中消除地磁场和模型中的不变量，剩下的就是干扰磁场，也就是下式中的ΔHg。整理可得

2 方向余弦获取

在目标磁探中，目标磁矢量未知，而三轴磁强计测量的是总磁场矢量，直接测量目标磁场的方向余弦是不可能的，必须利用总磁场的方向余弦求得目标磁场的方向余弦。

设地磁矢量为He，背景磁场矢量为Hb，He和Hb的夹角为α，如图1 所示。He和Hb的合成矢量为H，则通过三角几何可以求得He和H 的夹角β 的余弦为［5］

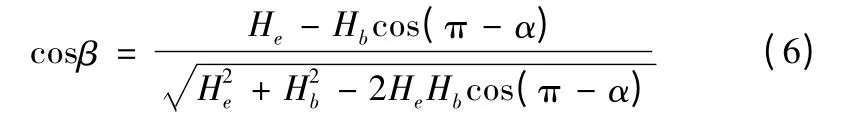
实际测量中，利用三轴磁强计测量地磁的方向余弦，但是三轴磁强计存在测量误差，这种误差对方向余弦产生影响。设三轴磁强计测量的三轴分量分别为Hx，Hy，Hz，则方向余弦的计算公式

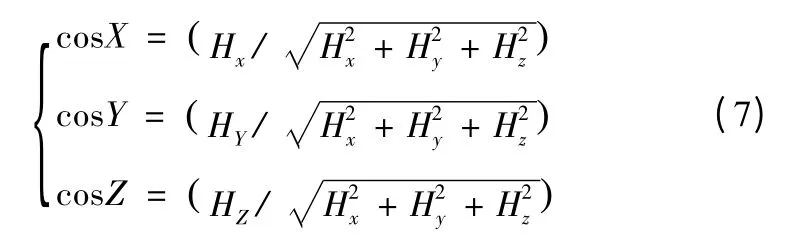
利用微分公式可以求得由于Hx，Hy，Hz的测量误差引起的方向余弦计算公式为

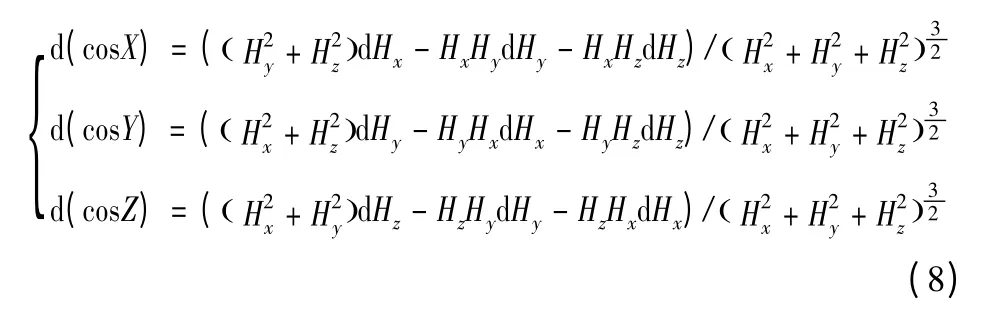
分析可以看出，由于三轴磁强计的测量误差，引起的的方向余弦的测量误差数量级为10-3nT，总地磁矢量和地磁矢量的夹角的余弦的数量级为10-5nT，同三轴磁强计由于测量误差引起的误差差两个数量级。在测量精度要求不大于0.2 nT 的情况下完全可以忽略这种误差对测量的影响。也就是可以用三轴磁强计测量的方向余弦代替目标磁场的方向余弦，不用考虑背景磁场对测量地磁方向余弦的影响。

3 基于偏最小二乘法的参数估计

由于高速飞行器背景磁场模型存在复共线性，利用高斯消元、迭代等常规方法无法精确求解，本文利用偏最小二乘法进行模型参数估计。

算法原理:设有q 个因变量y1，y2，…，yq和p 个自变量x1，x2，…，xp，为了实现自变量系数的估计，采集n 个样本点，构成数据表:X =［x1，x2，…，xp］n×p和Y =［y1，y2，…，yq］n×q。偏最小二乘回归分别在X 和Y 中提取主成分t1和u1，t1是x1，x2，…，xp的线性组合，u1是y1，y2，…，yq的线性组合。在提取这2 个成分时必须满足如下要求:t1和u1应尽可能地携带它们各自数据表中的变异信息;t1和u1的相关程度达到最大。

在第一个主成分t1和u1被提取后，及Y 对u1的回归，如果回归方程已经达到满意的精度，则算法终止。否则，将利用X 被t1解释后的残余信息以及Y 被u1解释后的残余信息进行第二次成分提取。如此往复，直到能达到一个较满意的精度为止。若最终对X 选取了m 个成分t1，t2，…，tm，将通过实施Y 对t1，t2，…，tm的回归(m ＜rank(A))，然后表达成Y 关于原变量x1，x2，…，xp的回归方程，可以实现对变量系数的估计。

为了消除X 矩阵中与Y 无关的信息，也就是测量数据的噪声，这要求X 的线性组合与Y 无关，满足下面方程

所以ξ 属于XY'的正交补空间。方程两边同时乘以X'Y，显然X'Y 不为零，则式(4)变为

由于 R(［X' Y］p×1)= R(［X' Y］1×p)= 1，故R(［X'YY'X］p×p)=1，因此X'YY'X 是秩为1 的方阵，ξ 为X'YY'X 特征值为零的特征向量，记X'YY'X 的p-1 个特征值为零特征向量为ξ1，ξ2，…，ξp-1。［ξ1，ξ2，…，ξp-1］张成的线性空间为W⊥，则ξ∈W⊥，ξ 可以表示成ξ1，ξ2，…，ξp-1的线性组合。令Φ=［ξ1，ξ2，…，ξp-1］，则ξ=Φγ。

为了尽量消除与因变量无关的信息，就要寻找使得Xξ=XΦγ 方差达到最大的γ。根据推导［5］γ 是使Φ'X'XΦ 具有最大特征值所对应的特征向量。记Φ'X'XΦ 较大特征值的特征向量为ζ1，ζ2，…，ζk(k≤p)，定义矩阵Γ =［ζ1，ζ2，…，ζk］，则Π=XΦΓ 就是X 矩阵中与Y 无关的信息。

因此将X 矩阵投影到Π 列向量所张成的正交补空间上，可以消除掉X 中与Y 无关的信息。根据最小二乘原理［5］，推导出正交投影算子为ΡH⊥=Π(ΠΠ')-1Π'，则得到的投影矩阵为

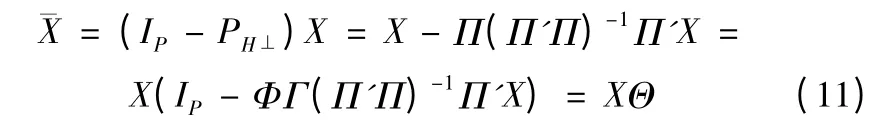
4 算法仿真分析

飞机的学习采用四航向法，即飞机在空旷高空地带(地磁场没有明显异常变化)，进行东西南北4 个方向的机动学习，每个方向分别做横滚、俯仰、摇摆标准机动。同步采样机进行16 位多通道同步采样。基于上述学习过程，对北纬55°空域进行了某个航次的四航向数据仿真，如图2 所示。

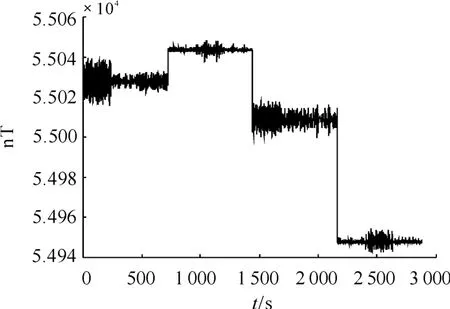
图2 四航向学习仿真数据

进行学习，基于偏最小二乘估计得到的飞机磁场17 个参数的值，与预置的真值比较，如表1。

对比分析可见，基于偏最小二乘回归估计求解高阶的复共线性方程，可以很好的将解的误差控制在10%以内，尤其是“大”数，解的误差＜5%，这为高精度实时补偿打下坚实基础。

对北纬40° ～60°的仿真数据进行实时补偿:图3(a)对某3 000 nT 量级磁源目标进行建模，计算得400 垂直距离，400 正横距处的目标信号，信号的峰峰值约为1.2 nT。图3(b)为探测光泵输出的磁场数据，迭加了图3(a)的目标信号，但背景噪声已经完全掩盖了目标信号。图3(c)为进行中值滤波(步长k=9)、高通通滤波(延时参数k =100)和布莱克曼窗平滑(宽度2 s)的磁场信号，目标信号在50 ～70 s的时间点上，还是被完全掩盖。图3(d)为进行了模型化滤波的结果。飞机干扰磁场在图3(c)信号的基础上，又被衰减90%以上，目标瞬态信号(70 s 时段信号)被较好的保留。

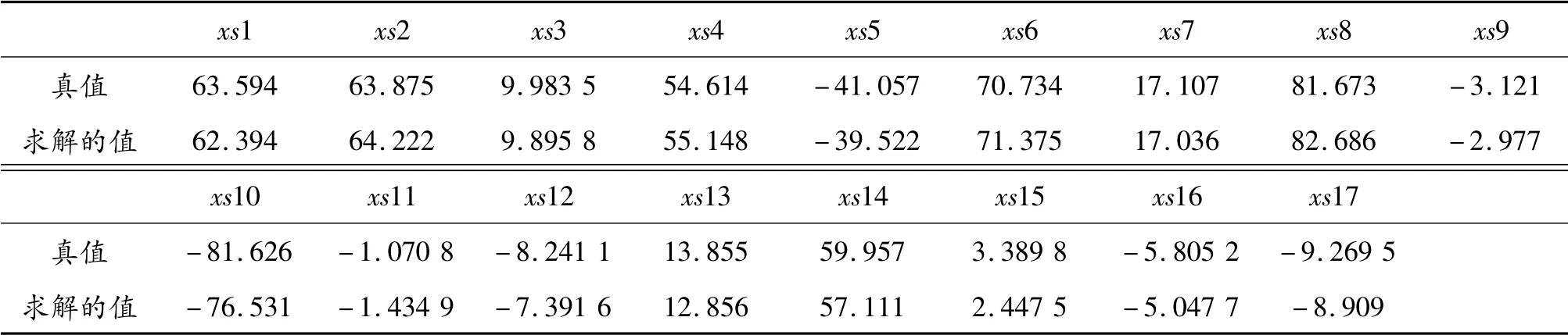
表1 飞机参数求解

结果对比分析可见，本文改进的17 参数的飞机磁场模型，能较好的拟合飞机自身的干扰磁场，利用磁场三分量获取方向余弦的方法合理、实用，基于偏最小二乘回归算法可以比较精确的求解高阶复共线性参数方程，使得模型化补偿算法能90%以上的补偿掉飞机背景干扰场，从而大大提高航空磁探系统对远场弱磁目标的探测能力。另外，由图2 对比可见，本模型的补偿算法拥有较好的时域分辨率，可以准确的保留多目标瞬态信号，有利于多目标的实时辨识。

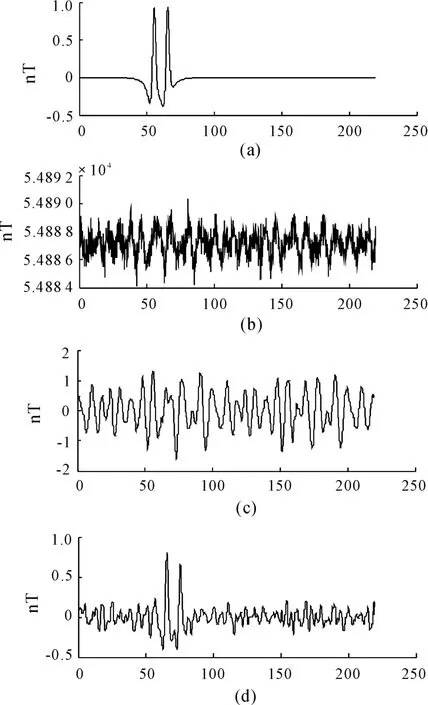
图3 飞机磁场探测模型化补偿效果

4 结束语

高精度航空磁探在民用和军用方面需求的提高，对飞机干扰磁场的建模精度有更高的要求，本文基于Tolles -Lawson 磁场模型，考虑了地磁总强度的变化引起的涡流场，改进飞机背景磁场模型，对方向余弦的获取做了分析，并基于偏最小二乘法对模型参数进行估计。对算法进行了数据仿真，结果表明模型化补偿的方法能有效的衰减飞机本身的磁场干扰，保留瞬态的微弱磁场信号，显著提高了信噪比。

［1］Tolles W E，Lawson J D.Magnetic compensation of MAD equipped aircraft［J］.Airborne Instruments Lab.Inc.，Mineola，N.Y.，1950(6):201-203.

［2］Tolles W E. Compensation of induced magnetic fields in MAD equipped aircraft［J］. Airborne Instruments Lab，OSRD 1386，1943(4):320-323.

［3］Leliak P. Identification and evaluation of magnetic field sources of magnetic airborne detector equipped aircraft［J］.IRE Trans Aerosp Navig Electron，1961(9):75-77.

［4］王金根，龚沈光，刘胜道.磁性目标的高精度建模方法［J］.海军工程大学学报，2001，13(3):49-52.

［5］吴文福.16 项自动磁补偿系统［J］.声学与电子工程，1993(4):14-21.

［6］何敬礼. 飞机磁场的自动补偿方法［J］. 物探与化探，1985(9):464-469.

［7］Bickel S H. Small signal compensation of magnetic fields resulting from aircraft maneuvers［J］.IEEE Trans.on AES.1979，AES-15(4):515-525.