一种基于五元圆阵的星载相位干涉仪定位求解法

【装备理论与装备技术】

一种基于五元圆阵的星载相位干涉仪定位求解法

李晓星，王磊

(中国电子科技集团公司 第三十六研究所, 浙江 嘉兴314033)

摘要：在星载5元圆阵的基础上，利用卫星在不同位置测得的信号相位差，提出了一种基于可能目标反解相位求最优的单星无源定位方法，给出了定位和去除模糊解的原理与计算过程，并用仿真验证了该方法在去定位模糊解的有效性。

关键词：，五元圆阵；单星无源定位；相位干涉仪；测向；解定位模糊

收稿日期：2014-10-16

作者简介：李晓星(1980—)，男，工程师，主要从事数字信号处理、无线电测向与定位研究；王磊(1982—)，男，工程师，硕士，主要从事数据挖掘、无线电测向与定位研究。

doi:10.11809/scbgxb2015.02.012

中图分类号：V423.43

文章编号：1006-0707(2015)02-0041-03

本文引用格式：李晓星，王磊.一种基于五元圆阵的星载相位干涉仪定位求解法[J].四川兵工学报，2015(2):41-43.

Citationformat:LIXiao-xing,WANGLei.SolvingMethodofPassiveLocationBasedon5-ElementUCASpacebornePhaseInterferometers[J].JournalofSichuanOrdnance,2015(2):41-43.

SolvingMethodofPassiveLocationBasedon5-ElementUCA

SpacebornePhaseInterferometers

LIXiao-xing,WANGLei

(No.36ResearchInstitute,ChinaElectronicsTechnologyGroupCorporation,Jiaxing314033,China)

Abstract:A method of passive location based on 5-element UCA spaceborne phase interferometers was put forward by using optimal value on the phase solution of possible targets. The computation method and algorithm of passive location and ambiguity solving method were given. The effectiveness of this method in locating the fuzzy solution was verified by simulation.

Keywords: 5-elementUCA;singlesatellitepassivelocation;phaseinterferometers;direction-finding;solvingpassivelocationambiguity

利用电子侦察卫星对辐射源进行测向定位在军事领域内有着广泛的应用，对于实施针对性电子干扰和军事打击具有重要作用。其中，单星测向定位法可快速定位辐射源，工作方式简单。文献[1]中提出了一种单星测向定位方法，用星上二维相位干涉仪测量来波信号相位差，进而求得辐射源的方位角和俯仰角，通过示向线与地球球面相交的方法确定辐射源位置。文献[2]中提出了在低轨卫星运动中多次测向、通过聚类处理获得定位结果的方法。

虽然文献[1]中提出了单星二维相位干涉仪定位的基本模型和方法，但没有解决二维相位干涉仪测向可能存在的相位模糊问题，文献[2]中利用低轨卫星运动过程中真实辐射源定位点位置收敛这一前提，消除了定位模糊，但也引入了可能的聚类结果参数敏感等新的问题。

本文以低轨星载五元圆阵的二维相位干涉仪测向为研究对象，结合文献[3]中的最小二乘相位最优拟合思路，实现了无模糊的无源定位计算。

1星载五元圆阵二维相位干涉仪定位原理

1.1五元圆阵二维相位干涉仪测向的求解模型

以图1中均匀分布的五元圆阵为例进行说明，某入射信号方位角为α，仰角为β，在圆心处虚拟构造阵元0，假设其相位为0°，由φi=φi-φ0，得到阵元1~5的相位表达式如下

(1)

其中：d为任一阵元至虚拟阵元的基线长；λ为波长；D为图 1中五角星对角基线长。

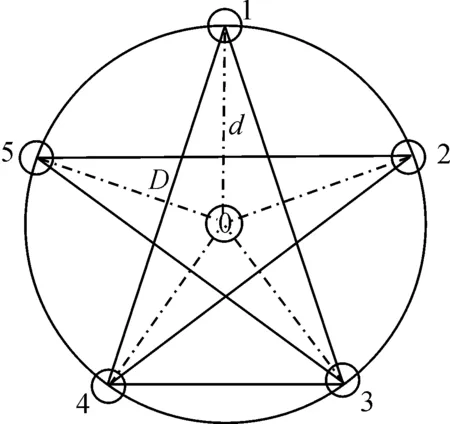
图1　五元圆阵

由式(1)，则对角基线的相差组为

(2)

由式(1)，得到如下

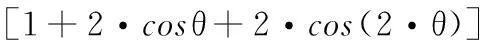
(3)

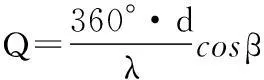
由阵元关系，得如下

(4)

化简后得到

(5)

由式(2)、式(5)，可得到入射仰角及方位角的计算公式：

(6)

(7)

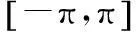
(8)

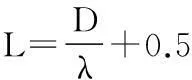
1.2星载测角定位求解模型

记在瞬时t时刻，卫星轨道坐标系OX、OY、OZ三轴在WGS-84坐标系中的方向余弦分别为：lx，ly，lz，mx，my，mz，nx，ny，nz；卫星当前时刻的位置(WGS-84)：gpsx，gpsy，gpsz；卫星当前时刻的速度(WGS-84)： vx，vy，vz。

设为xq，yq，zq为卫星轨道坐标系上的一点，则转换为WGS-84坐标下的xw，yw，zw公式如下

(9)

卫星测得辐射源目标方位角为α，仰角为β，假定卫星辐射源两点距离为d，则取入射波上的一点，则在卫星测向坐标系中的坐标定义为

(10)

(xt′,yt′,zt′)由结合卫星姿态参数和式(9)、式(10)，转换为WGS-84坐标(xt,yt,zt)后，与(gpsx,gpsy,gpsz)确定一条直线，与地球面的交点即为定位点。联立一下方程(9)、式(10)、式(11)、式(12)，即可得出定位点(与卫星距离较近的点即定位点)。

(11)

(12)

其中：a=6 378.145km；b=6 356.755km。

2求解方法

假定卫星飞行过程中，完成对辐射源P的n次相位采集，则得到一组天线阵元的相位差，如下，(Δφij)1…(Δφij)k…(Δφij)n，其中i∈{1,2,3,4,5},j=mod(i+2,5)。

任取一组相位(Δφij)k，由式(8)，假设-L≤ki≤L，i∈{1,2,3,4,5}，则可以得到(2L+1)5组相位组合，结合卫星相位提取时刻的轨道数据，用式(6)~式(12)可以得到(2L+1)5组测角结果和定位结果(α，β，w)j，1≤j≤(2L+1)5，w为方位角α、俯仰角β对应的定位结果。

由式(8)中wj必定存在一个最优值，其余为模糊值。对每一个的wj值，结合t1~tn时刻的相位测量值和轨道参数如下

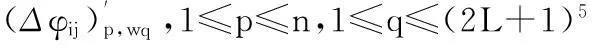
基于最优定位点的理论相差与实测值相差符合性最优这一原则，最小二乘最优得到

(13)

当V值达到最小时，对应的Wq为最优定位结果。

以上求解过程中，只是求解除了第k组中的最优定位结果，对于辐射源天线指向天顶的目标，第k组可以选择信号幅度最强的一组，因为此时的俯仰角最高，理论定位误差小。对于其他情况可以选择多组k值，则得到多个最优定位结果，由于不存在模糊问题，可以直接统计出定位统计结果。

此外，由于多个阵元的存在，导致存在(2L+1)5组组合，在优化过程中可以利用阵元的不同长短基线组合的回路去除大部分的组合，如图 1所示，利用Δφ14+Δφ43+Δφ31=0可去除部分组合项。

3算法的仿真实验

用STK仿真一颗轨道高度为400km的太阳同步圆轨道卫星，假定辐射源位置(经度-84°，纬度33.8°)，在不考虑卫星姿态的情况下，可以得到卫星与辐射源的相对的方位角和俯仰角。

利用式(1)可以得到对应的测量Δφij，并加入均方根20°的相位误差。另设定卫星在运动过程中每1s完成一次测向定位，共仿真5min，俯仰角变化，如图2所示。

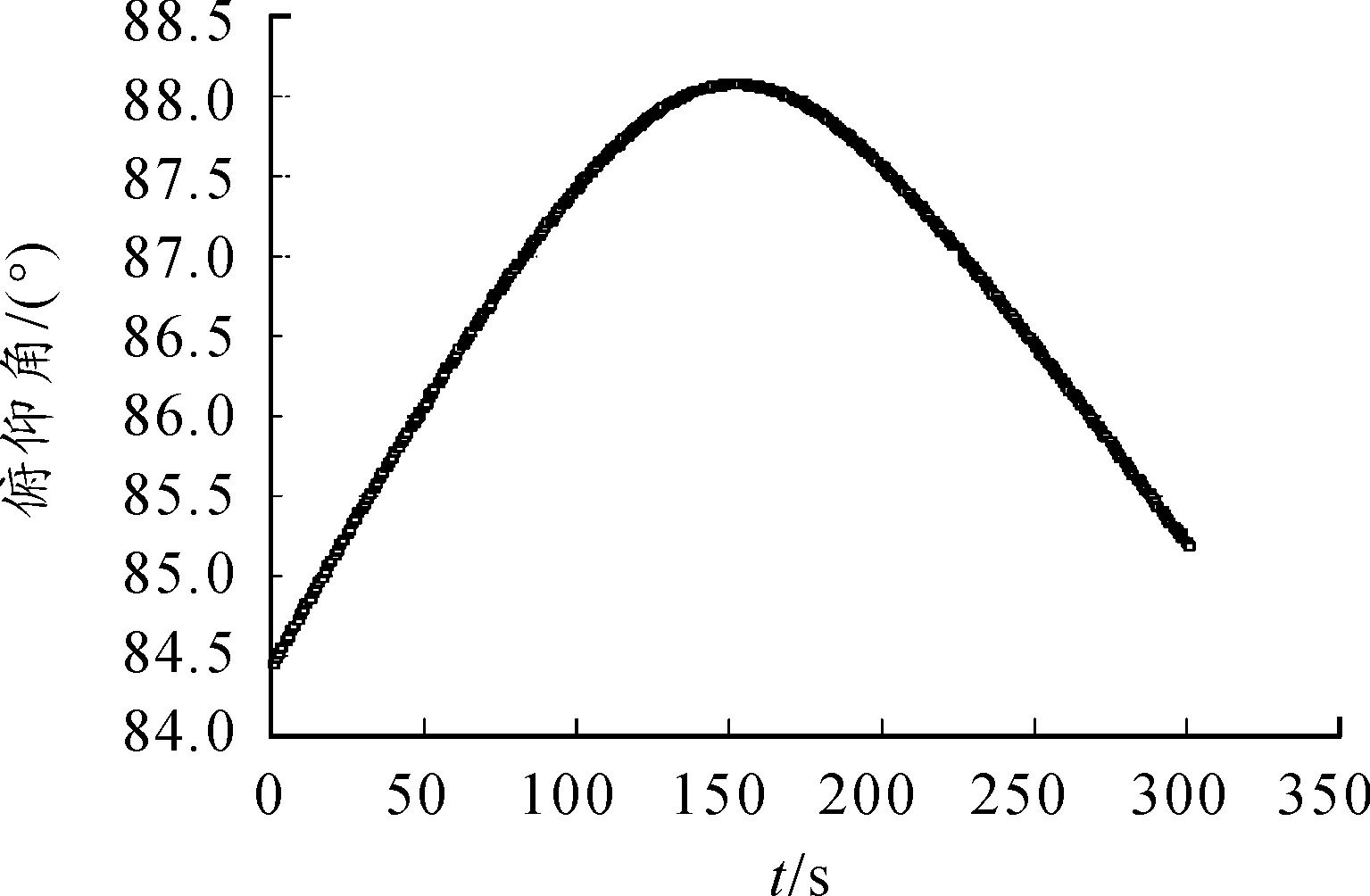
图2　卫星与辐射源的仰角变化图

取俯仰角88.07°时的卫星轨道位置，利用式(6)、式(7)得到所有可能的测角结果，利用式(9)～式(12)可以得如图3所示结果。

按前述的求解方法，可以得到式(13)的V值分布如图4所示。其中V最小时对应的位置即辐射源的最优位置(经度84.40°，纬度33.95°)，证明了算法的有效性。

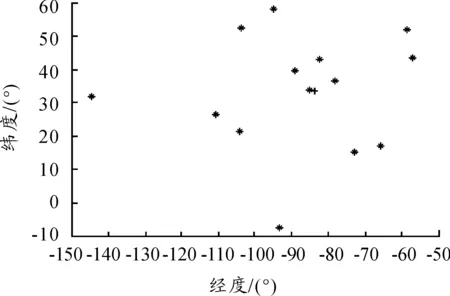
图3　所有可能的定位结果示意图

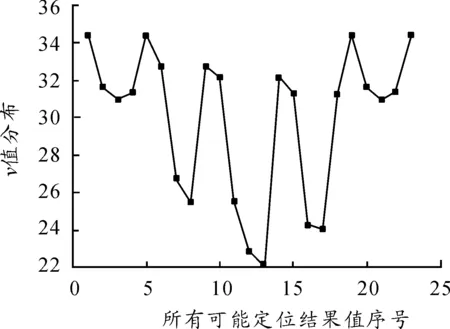
图4　 V值分布

4结束语

本文提出了一种基于五元圆阵的星载相位干涉仪定位求解法，相比最小二乘测向算法，具有运算量小的优势，适合星上实现；相比单次瞬时测量的测向定位算法，由于本方法利用了一轨中多次测量数据(入射角的不断变化)，具有较强的解模糊能力和较强的测量误差的容差能力，具有一定的工程应用价值。后续研究，考虑利用本文提出的定位结果，引导计算多次瞬时测量的解模糊结果，再利用聚类算法提高测量精度。

参考文献：

[1]陆安南.单星无源测向定位及精度分析[J].电子科学技术评论，2000(1):696-700.

[2]陆安南.基于模糊测向结果的单星无源定位法[J].电子对抗，2002(3):6-11.

[3]陆安南，杨小牛.最小相位误差单星无源定位法[J].上海航天，2007(3):6-9.

(责任编辑周江川)