新课程理念下中学数学总复习点滴思考—学会反思、走出题海
华中师范大学第一附属中学朝阳学校 刘振华
在当前初三总复习阶段中,许多学生整天埋头于题海,认为“不进题海难攻题”。题海战术究竟灵不灵?我认为学生适量练题是非常必要,但靠题海战术是不可取的。解题并不是单纯为求得问题的结果,真正的目的是为了提高学生运用知识的能力。面对浩瀚题海,老师应把题海留给自己,而多教会学生进行反思、整理、归纳、总结,增强学生清醒的复习意识,逐步学会自主学习。
荷兰数学家和教育学家费赖登塔尔认为:“反思”是数学思维的特征,是数学创造强有力的动力。我认为在复习中可从以下几个方面引导学生反思。
一、对数学概念的反思
数学概念是人类对现实世界的空间形式和数量关系的简明概括及反映。它是数学学科的精髓,是构建知识网络的出发点,也是中考考查的重点,是学生进行计算、解答、证明的依据。
(一)整理同属种概念,形成知识体系
在初中数学中,绝大部分概念间的关系是属种关系,因此给概念下定义也主要以属种定义为主。
例如,复习四边形这一单元时,我借助图形先讲解“属”概念:两组对边分别平行……然后再给出“种差”:一个角是直角……学生在图示的启示下复习平行四边形、矩形、菱形、正方形、梯形、等腰梯形、直角梯形等概念。
(二)判别反思,准确表述概念
数学概念是用科学的精炼的数学语言概括表达出来的,它所揭示事物的本质属性必须确定、无矛盾、有根有据、合情合理的。
在复习时,设置一些较易混淆的概念,让学生判断、反思概念,使学生更能准确表述概念,促进学生思维的严密性、深刻性。
例如,下列说法正确的是( )
A、有理数都是有限小数
B、带根号的数是无理数
C、无限小数都是无理数
D、无理数都是无限小数
让学生通过判定,准确表述无理数、有理数的概念,选择 D。
(三)错误中反思,真正认识概念本质
每一个数学概念都有这样或那样的限制条件,如果忽略了这些条件就可能导致解题错误。因此在解题后帮助学生从对错误的反思中激起对概念更为深刻的正面思考,使学生真正认识概念的本质。
二、对基本问题的反思
数学中的基本问题包括公式、法则、性质、公理、定理、基本图形、图象等。复习时反思基本问题是否真正弄懂弄通,基础知识能否真正掌握,平时碰到的问题中有哪些可归结为基本问题。
例如,有理数加法用加法法则,判定三角形全等用全等三角形判定定理等。
三、对数学思想方法的反思
数学思想方法是解题的灵魂。初中阶段经常运用的数学思想方法有:转化思想、数形结合思想、分类讨论的思想、方程的思想、函数的思想等,突出这些数学基本思想方法就相当于抓住中学数学知识的精髓。
(一)转化思想
前苏联数学家雅诺夫斯卡娅在回答解题意味着什么时说:“解题就是意味着把所要解决的问题转化为已经解过的问题。”
例 :已知a是方程x2+3 x +1 = 0的根,求(2 a + 1)2− 2 (a2−a )+4的值。
解答此题时,学生可解一元二次方程求出x的值即a的值,但x非整数容易出错。于是,引导学生仔细观察,发现可根据方程根的概念,把a代入得a2+3a +1 = 0,然后把a2+3a 看作整体再代入化简式中。通过等价变换,把繁难问题转化为简单问题来处理。
(二)数形结合思想
我国数学家华罗庚曾指出 :“数无形时少直观;形无数时难入微”。这充分说明数与形的辩证关系。教师在指导学生解题时,应有意识地运用数形结合的思想,由形到数,由数到形的多次反复,寻求最佳的解答途径,使学生能从中体会到数形结合思想在解题中起到的重要作用。
第一,以“形”直观表达“数”,可以把抽象的数转化为形,从而避免繁琐的运算,简捷解题。
第二,以“数”精确研究“形”,可以把复杂的“形”转化为具体的“数”,从而使问题更容易解决。
(三)分类讨论的思想
在解题过程中,当条件或结论不唯一时,会产生几种可能性,就需要分类讨论。
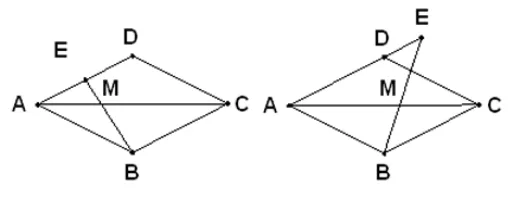
例如,己知菱形ABCD的边长是6,点E在直线AD上,DE=3,连接BE与对角线AC相交于点M,求MC;AM的值。
分析:学生自己画图分析,在充分理解“点E在直线AD上”的基础上,对题目进行分类讨论。
(四)方程的思想
许多数学问题的解决都离不开方程,例如,函数表达式或方程中未知数的确定,几何题中边长、角度、面积的求解、应用题等,都可以通过寻找已知量与未知量之间的相等关系,适当设元,列出方程或方程组,从而解决问题。
(五)函数的思想
函数所揭示的是两个变量之间的对应关系,就是一个量的变化引起了另一量的变化。在数学中总是设法将这种对应关系用解析式、图象或表格表示出来。这样可充分运用函数的知识、方法解决问题。
四、对常见错误的反思
俗话说“吃一堑,长一智”。对错误的进行反思,从中得到教训,更能使人印象深刻。在复习过程中,还要特别注意引导学生对常出现错误进行反思:出现错误的原因是属知识的遗忘,还是粗心大意,找出出错的症结,从而纠正错误,同时也加深对知识的理解。
在复习过程中,教师要经常引导学生对所做的题目进行检查,对所用的知识点进行回顾与反思,帮助学生整理思维过程,概括解题的关键,提炼数学思想方法,总结成功的经验和失败的教训,启发学生剖析问题的本质,寻找问题之间的内在联系,探索一般规律,提高思维能力。引导学生反思,有利于帮助学生更好地掌握知识、运用知识,培养学生良好的思维品质,提高学习效率,真正走出题海。
——记我的原创感悟

