浅谈勾股定理的应用

郑永平

【中图分类号】G633.41 【文献标识码】A 【文章编号】2095-3089（2015）06-0247-02

勾股定理的由来：勾股定理也叫商高定理，在西方称为毕达哥拉斯定理.我国古代把直角三角形中较短的直角边称为勾，较长的直角边称为股，斜边称为弦.勾股定理为：两直角边的平方和等于斜边的平方表示方法：如果直角三角形的两直角边分别为a，b，斜边为c，那么

勾股定理是初中数学，重要的一部分，在实际中如果能巧妙的运用勾股定理，会极大提高学生学习数学的乐趣。

题型一：利用勾股定理测量长度

例题 如果梯子的底端离建筑物9米，那么15米长的梯子可以到达建筑物的高度是多少米？

解析：这是一道大家熟知的典型的“知二求一”的题。把实物模型转化为数学模型后，.已知斜边长和一条直角边长，求另外一条直角边的长度，可以直接利用勾股定理！

题型二：勾股定理和逆定理并用

例题 如图3，正方形ABCD中，E是BC边上的中点，F是AB上一点，且 那么△DEF是直角三角形吗？为什么？

解析：这道题把很多条件都隐藏了，乍一看有点摸不着头脑。仔细读题可以发现规律 ，可以设AB=4a，那么BE=CE=2 a，AF=3 a，BF= a，那么在Rt△AFD 、Rt△BEF和 Rt△CDE中，分别利用勾股定理求出DF，EF和DE的长，反过来再利用勾股定理逆定理去判断△DEF是否是直角三角形。

题型三：折叠问题

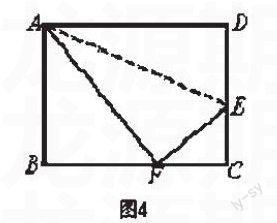
例题 如图4，已知长方形ABCD中AB=8cm，BC=10cm，在边CD上取一点E，将△ADE折叠使点D恰好落在BC边上的点F，求CE的长.

解析：解题之前先弄清楚折叠中的不变量。合理设元是关键。

题型四：旋转问题：

如图，△ABC是直角三角形，BC是斜边，将△ABP绕点A逆时针旋转后，能与△ACP′重合，若AP=3，求PP′的长。

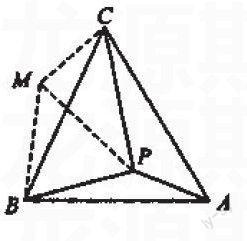
变式1：如图，P是等边三角形ABC内一点，PA=2，PB= ，PC=4，求△ABC的边长.

分析：利用旋转变换，将△BPA绕点B逆时针选择60°，将三条线段集中到同一个三角形中，根据它们的数量关系，由勾股定理可知这是一个直角三角形.

题型五：关于勾股定理在实际中的应用：

例题、如图，公路MN和公路PQ在P点处交汇，点A处有一所中学，AP=160米，点A到公路MN的距離为80米，假使拖拉机行驶时，周围100米以内会受到噪音影响，那么拖拉机在公路MN上沿PN方向行驶时，学校是否会受到影响，请说明理由；如果受到影响，已知拖拉机的速度是18千米/小时，那么学校受到影响的时间为多少？

分析此题是把实际问题转化数学中勾股定理来解决的。

解：作AB垂直于MN交MN于B点，可知AB=80m<100m

故会受到影响

取B点右侧点C，连AC，设AC=100m

根据勾股定律BC=60，可知拖拉机在BC上行驶会影响学校

相应的，取B点左侧点D，设AD=100m

DB=60，可知拖拉机在DB上行驶会影响学校

故拖拉机在DC上行驶会影响学校，DC=BC+DB=120m

18km/h=5m/s 120/5=24秒

学校受到的影响的时间为24秒

题型六：关于最短性问题

例题如图，圆柱的轴截面ABCD是边长为4的正方形，动点P从A点出发，沿着圆柱的侧面移动到BC的中点S的最短路径长是多少？

分析：在运用勾股定理解决有关问题时，常常需要将一些线段通过平移、旋转、翻折等运动变化从而转化到一个直角三角形中，即转化思想.

求几何体的表面的最短距离，可联系我们学过的圆柱体的侧面展开图，化“曲面”为“平面”，再寻找解题的途径.如右图，可得展开图中的AB长为2π，BS为2，根据勾股定理，在RtΔABS中，得AS=2 所以，动点P从A点出发，沿着圆柱的侧面移动到BC的中点S的最短路径长为2 。

勾股定理在初中数学中是一颗灿烂的明珠，常用于解直角三角形试题，涉及到边的计算、角的计算、直角三角形的判定、翻折、爬行、图形变换、实际应用等题型，熟练掌握有关勾股定理的常见题型的解法对学生学好勾股定理的内容有着很大的帮助。