车辆-轨道-桥梁竖直耦合振动程序设计及仿真

雷震宇 闫 旭

(同济大学铁道与城市轨道交通研究院，201804，上海∥第一作者，副教授)

轨道交通车辆在高架桥上运行时产生的结构振动和噪声问题一直困扰着人们的生活。轮轨复杂的非线性接触是该问题的核心。在轮轨关系的仿真分析中，应用最广泛的两款软件为 ADAMS 和SIMPACK AG。虽然，两者的轮轨模块可以很好地体现车辆和轨道的耦合作用，但对需要考虑柔性基础(桥梁)的刚柔混合模型的仿真，两款软件都需要通过与外部有限元软件的接口实现对复杂柔性体的支持，不但操作繁琐，而且参数设置不当还可能会影响柔性体传输的正确性，使得仿真结果的可参考性很差［1］。鉴于现有软件对车辆－轨道－桥梁耦合系统的仿真功能还有待完善，许多学者都通过直接编程的方式对车桥耦合系统的动力特性进行了相关研究［2－9］。但是，前人的研究多数没有考虑轨道的参振作用，或是车辆和轨道的模型过于简化而无法准确得到轨道结构的振动特性。本文从耦合系统的振动微分方程出发，建立了完整的车－线－桥竖向耦合模型，并以工程中常用的桥上弹性支承块式无砟轨道为例，利用MATLAB 软件编写了求解耦合系统竖直振动时变特性的程序;考虑到系统各组成部件动力特性的差异和部件之间耦合作用的强弱，对车辆、轨道和桥梁分别予以合理简化，在程序编写时将系统化整为零，将大型非线性时变微分方程组分块求解，降低了整体求解对计算机内存和速度的要求，节省了计算成本。仿真结果显示，简化模型和计算程序可以保证分析的准确性。

1 竖向耦合振动模型的建立

1.1 物理模型的简化

对物理模型作了如下的简化:

1)车辆采用具有二系悬挂的客车模型［10］。一系和二系悬挂简化为线性弹簧和粘性阻尼;轮对、构架和车体简化为7 个刚体，考虑轮对的沉浮运动、构架和车体的沉浮和点头运动，共有10 个自由度;轮对与钢轨的接触用Hertz 非线性弹簧模拟。

2)轨道选用弹性支承块式无砟轨道。钢轨视为连续弹性离散点支撑的Euler 梁，只考虑竖向弯曲振动;扣件和胶垫的作用通过线性弹簧和粘性阻尼模拟;将弹性支承块视为刚性质量块，只考虑竖向振动;桥梁跨度范围之外的支承块用弹簧和阻尼与刚性基础连接;将道床板和混凝土底座视为桥梁的一部分，考虑轨道高低不平顺的影响。

3)桥梁简化成线性等截面简支梁，只考虑平面内的弯曲振动，道床块与桥面的相互作用通过线性弹簧和粘性阻尼模拟，忽略桥梁支座和桥墩的变形。

经过简化后的车辆－轨道－桥梁竖向振动系统如图1所示。

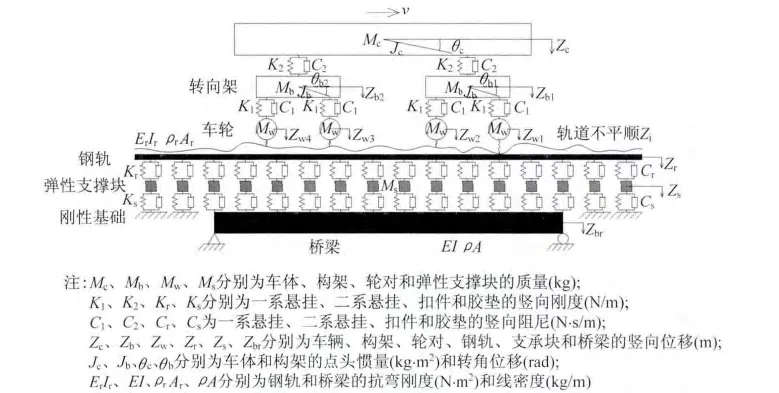
图1 车辆－轨道－桥梁竖向耦合振动简化模型

1.2 耦合振动方程的推导

耦合系统振动方程的建立方法主要有分离子系统法和整体法两种。两种方法各有其优缺点。分离子系统法能够体现子系统之间复杂的相互作用力和位移协调关系，可以对子系统单独求解，且系统矩阵不具时变性，减小了计算工作量，但建模较为繁琐［11］;整体法建模思路清晰，可以避开轮轨关系的不确定性，但需要求解大型时变非线性方程组而非常耗时。为研究轮轨之间的相互作用，同时为求解方便，本文利用子系统建模法建立系统振动方程，以轮轨接触面和道桥接触面为界，将耦合系统分为车辆子系统、轨道子系统和桥梁子系统，各子系统之间通过位移相容条件和静力平衡条件进行耦合。其方法如下。

1.2.1 车辆子系统的竖向振动方程

根据达朗贝尔原理，可得多刚体组成的车辆系统的动平衡方程［10］，写成矩阵的表达形式为

式中:

Mv——车辆子系统的质量矩阵;

Kv——车辆子系统的刚度矩阵;

Cv——车辆子系统的阻尼矩阵;

Fr－v——车辆子系统的广义荷载向量;

uv——车辆子系统的广义位移向量。

1.2.2 轨道子系统的竖向振动方程

钢轨的振动方程为4 阶偏微分方程，采用振型叠加法［12］得到正则化坐标下的振动方程为

式中:

qk——钢轨 k 阶模态坐标;

lr——钢轨计算长度;

pwrj——第 j号轮对的轮轨力;

Ns——计算范围内钢轨支点总数;

Zk(x)——钢轨振型函数;

xsi——第i 个钢轨支点的位置;

xwj——第 j号轮对的位置。

根据不同位置处弹性支承等效质量块的受力状态分别建立Ns个振动方程，并将钢轨和等效质量块的振动方程在广义坐标下进行耦合，最终得到矩阵表达形式的轨道子系统的振动方程为

式中:

Mrs，Krs，Crs，urs——分别为轨道子系统的质量矩阵、刚度矩阵、阻尼矩阵和广义位移向量;

Fv－rs，Fbr－rs——分别为车辆和桥梁对轨道的广义荷载向量。

1.2.3 桥梁子系统的竖向振动方程

用平面梁单元将桥梁沿跨度均分，保证在弹性支承块底部都有对应桥面节点。选定梁单元的位移模式为线性函数，单元质量矩阵采用一致质量矩阵，利用最小势能原理和坐标转换矩阵得到整体坐标下梁单元的单元刚度和质量矩阵;将单元刚度矩阵和质量矩阵进行扩展，集合成整体刚度和质量矩阵。整体阻尼矩阵采用Rayleigh 阻尼，加入节点力后可得到桥梁竖向振动的有限元矩阵方程

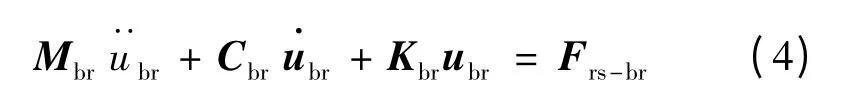
式中，Mbr，Kbr，Cbr，Frs－br，ubr分别为桥梁子系统的质量矩阵、刚度矩阵、阻尼矩阵、广义荷载向量和广义位移向量。

1.3 耦合方程的数值解法

3 个微分方程组式(1)、式(3)和式(4)的右端荷载项都包含相邻子系统的位移向量，体现了方程之间的耦合关系。借助数值方法在时域内对3 个子系统分别进行求解。采用显－隐式相结合的方法，在每一个时间步内，采用新型快速显式积分法［10］求解车辆子系统和轨道子系统;采用隐式积分法中的Newmark－β 积分法［13］求解桥梁子系统，最终可以得到系统的时域振动响应。

2 分离子系统法程序设计流程

直接积分法中的显式积分法是条件收敛的，时间步长和时间步的选取对程序的稳定性和计算精度影响很大［14］。一般要求的积分时间步长要小于所感兴趣的系统最小振动周期的1/10［15］，并且轮轨之间的非线性接触导致耦合方程的求解对初值的依赖性很大，呈现出“混沌”特性。在轮轨脱离的瞬间，钢轨的模态加速度很大，对模态响应进行显式积分后的误差累积很可能导致计算发散。因此，在程序设计时，通过对钢轨与支承块接触点的位移和速度进行控制，反推钢轨模态坐标，可以保证积分的稳定性。经过调试，综合考虑到计算效率，最终决定的积分时间步长为0.000 2 s，可以精确分析系统500 Hz 以内的振动情况。分离子系统法程序设计流程如图2所示。

图2 分离子系统法程序设计流程

3 程序校核算例

3.1 模型参数

车辆选取 HSC 型车辆，具体参数详见文献［10］，轨道和桥梁参数取值如表1所示。

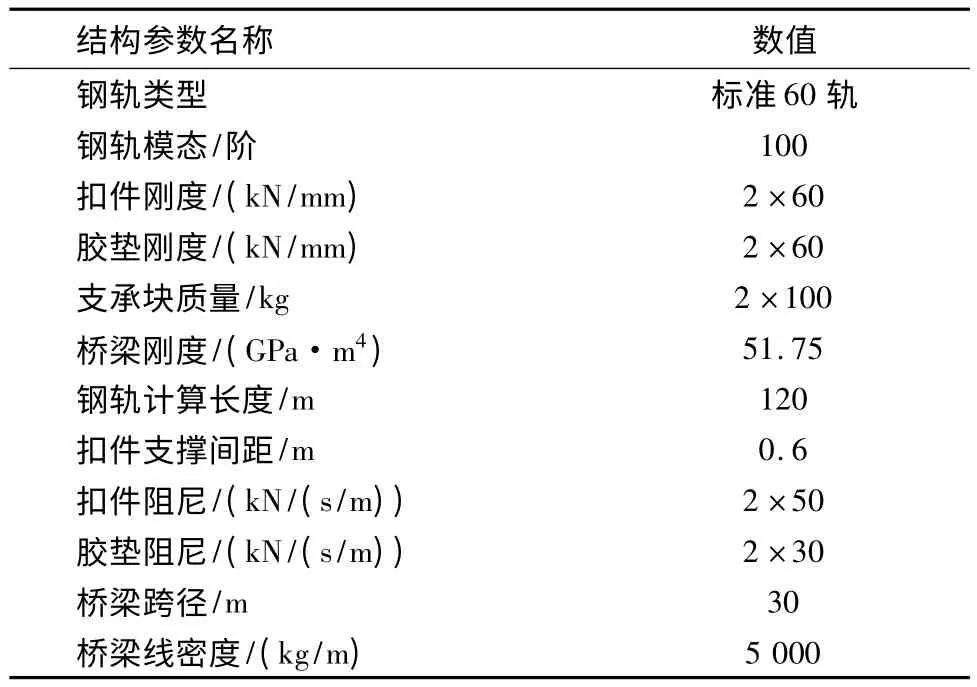
表1 轨道和桥梁结构参数

由于桥梁单元大小对耦合系统动态响应的影响很小［16］，桥梁划分为100 个单元进行计算。选取美国六级谱轨道高低不平顺为系统激励源［17］，利用程序绘制轨道不平顺样本曲线，以分析桥梁振动特性，描绘列车从进入桥梁到驶出桥梁过程中的钢轨、支承块及桥梁在不同时刻的变形状态和系统关键点的位移响应时程曲线，验证程序的可靠性。

3.2 轨道不平顺模拟及精度验证

采用三角级数法生成轨道不平顺样本，采样间距为0.1 m。钢轨计算长度内共采集样本1 200 个，取空间频率范围为 0.01 ～0.5 Hz，频率带宽为 0.01 Hz，则生成的轨道竖向不平顺样本如图3所示。

图3 美国六级谱轨道高低不平顺模拟曲线

利用平均周期图法对模拟的不平顺数据进行离散傅里叶变换，求得不平顺样本的功率谱密度，并与理论谱密度曲线进行对比。图4 显示了模拟曲线的谱密度与理论要求的谱密度在目标空间频率内基本吻合，说明模拟的有效性。

3.3 桥梁振动特性

利用MATLAB 软件编写了有限元法求解简支桥梁前6 阶竖向无阻尼自由振动频率和振型的程序［18］，结果如表 2所示。由表 2 可以看出，桥梁主要振动频率在200 Hz 以内。

图4 美国六级谱轨道高低不平顺功率谱密度曲线

3.4 程序的有效性验证

以钢轨左端为整体坐标原点，行车方向为x 轴，坐标原点x=0，桥梁处在x=45 ～75 m 范围内。初始时刻列车、轨道和桥梁都处于各自的静平衡位置，且处于静止状态;列车前转向架前轮处于x =30 m 处，轮轨相互接触但无挤压。不计初始变形，给列车水平向初速度作为系统初始激励，所有仿真结果都基于此初始条件。仿真距离取80 m，自x=40 m 处开始考虑轨道不平顺，为防止轨道高差突变对程序收敛性的影响，在 x=35 ～40 m 范围内引入 5 m 的缓和曲线，以保证轨道不平顺线性缓慢增加。

假定车辆以50 m/s 的速度运行，前转向架前轮在 0.3 s、0.6 s 和 0.9 s 到达桥头、跨中和桥尾，后转向架后轮在 0.71 s、1.01 s 和 1.31 s 到达桥头、跨中和桥尾，选取这6 个时刻的状态进行参考，按照时间先后顺序绘制钢轨、支承块和桥梁的位移状态如图5a)～5f)所示。图像显示，程序可以有效描绘耦合系统组件的状态变化。

当车辆以50 m/s 的速度经过高架桥区段时，钢轨中点、中间支承块和桥梁跨中点的时程和频谱(对数坐标)曲线如图6所示。

由图6a)可知，钢轨和支承块的时程曲线各有4个峰值，分别对应车辆的4 个轮对刚好经过该点的时刻;车轮作用点处的钢轨位移很大，作用点附近的钢轨位移很小，甚至为0，响应波形符合客观实际;桥梁时程曲线只有2 个峰值，这是由桥梁振动的低频特性造成的，在转向架的前后轮先后经过桥梁跨中点的时间段内，桥梁挠度来不及回弹，2 个峰值分别对应车辆的前后转向架刚好经过桥梁跨中点的时刻。

由图6b)可知，桥梁振动频率分布在0 ～200 Hz，主要频率成分集中在5 Hz 以内。这说明桥梁以一阶弯曲振动为主，桥梁实际振动频率比无阻尼振动频率低。而钢轨和支承块的振动频率分布范围较宽，在0～500 Hz，且以低于20 Hz 的低频振动为主;钢轨和支承块的频率分布大致相同，100 ～200 Hz 的频率成分所占比重比桥梁在同频段内的比重大。

图5 钢轨、支承块和桥梁不同时刻的位移状态图像

4 仿真结果探讨

4.1 轨道不平顺对系统动力响应的影响

车辆速度取为50 m/s，当轨道完全平顺和轨道不平顺时，轮轨相互作用力、钢轨中点竖向加速度和前转向架前轮的竖向加速度时程曲线如图7 和图8所示。图7、图8 中时间轴从0.2 s 开始显示，原因是程序在开始运行阶段，对初始条件需要经过多次迭代以达到系统稳定，因此该时间段内的数据没有实际参考意义，故此舍去。

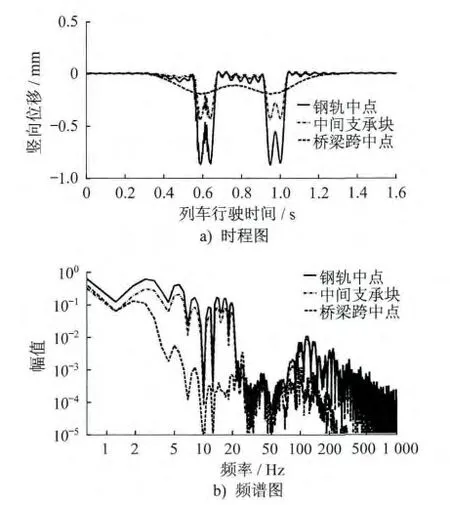
图6 钢轨中点、中间支承块和桥梁跨中点的时频图

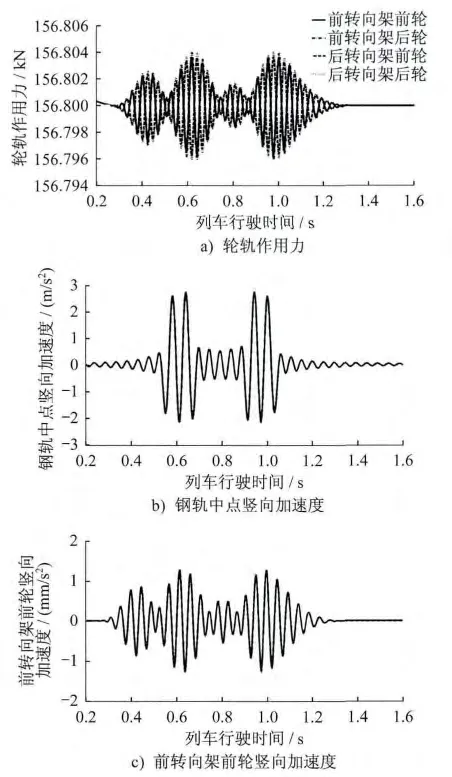
图7 平顺轨道的系统动力响应

图8 不平顺轨道的系统动力响应

图7 和图8 的对比说明，轨道不平顺对系统动态特性影响很大。轨道平顺性良好时，轮轨作用力在轴重附近有规律地上下波动，其最大值为156.804 kN，钢轨中点和前转向架前轮的竖向加速度峰值都很小。此时车辆、轨道和桥梁的动力作用不明显，轮轨密贴接触，列车运行十分平稳。轨道不平顺时，轮轨作用力仍围绕轴重上下波动，但波动剧烈、杂乱无章，多次出现轮轨力为0，即某车轮与轨道脱离的状态;轮轨冲击产生的最大轮轨力为527.5 kN，比轨道平顺时增大了2.36 倍，钢轨和车轮的竖向加速度峰值比轨道平顺时分别增大500 倍和40 000 倍，说明轨道不平顺是车辆－轨道－桥梁耦合振动系统的重要激励源之一。

4.2 车辆速度对系统动力响应的影响

在轨道不平顺相同的前提下，车辆速度在20 m/s ～80 m/s 之间取值，不同车速条件下耦合系统的动力响应结果如表3所示。表3 显示，车辆速度对轮轨作用力、钢轨加速度和支承块加速度的影响很大，且在高速时影响突出;但对车体和桥梁加速度及系统位移几乎没有影响，这是由耦合系统传递函数本身性质决定的。对于车辆－轨道－桥梁非线性耦合系统来说，车辆速度作为输入信号主要通过改变轮轨冲击力，进而改变钢轨和车轮的加速度对系统起作用，因此，速度对轮轨力响应和钢轨加速度响应的影响很明显。

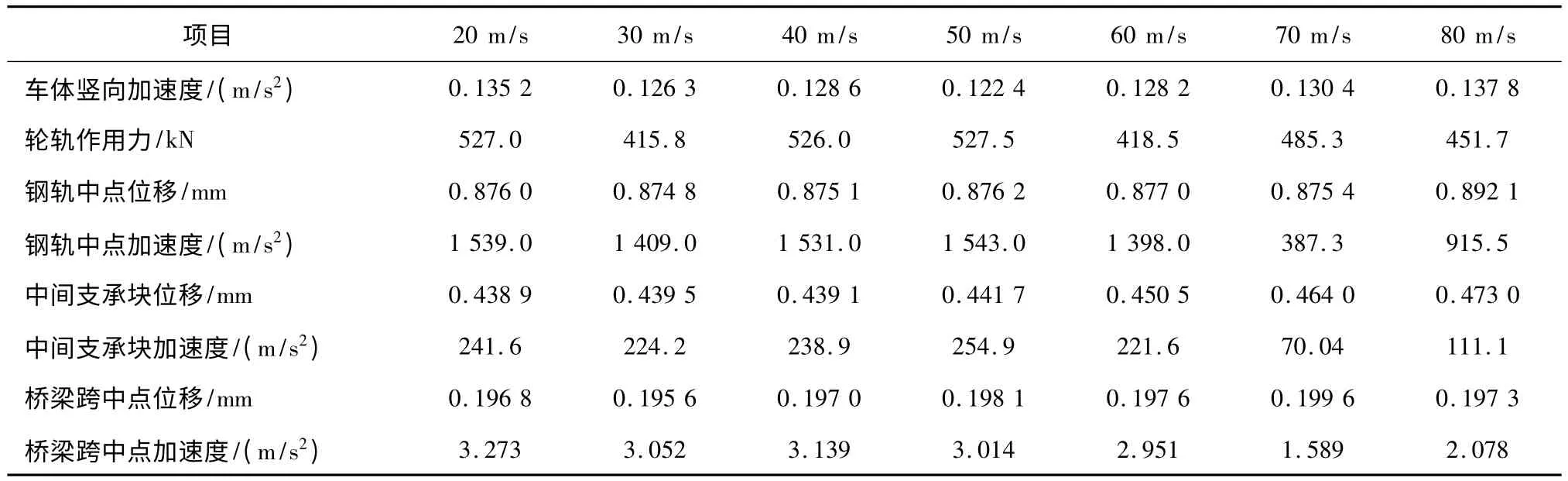
表3 系统动力响应随车速的变化值

经过一系、二系悬挂和轨道二级减振系统的削弱作用，传递到车体和桥梁的加速度很小，变化不明显。直接积分法中位移变化量与加速度变化量之间为时间步长的平方倍关系，在时间步长足够小时，轮轨高频冲击虽然产生很大的轮轨力和钢轨瞬态加速度，但位移变化量几乎为0。因此，系统位移响应受车辆速度的影响很小。

4.3 扣件和胶垫竖直刚度对系统动力响应的影响

在轨道不平顺相同的条件下，车速取50 m/s，扣件和支承块下胶垫竖直刚度在20 ～100 kN/mm之间取值，不同刚度条件下耦合系统的动力响应如图9所示。

图9 钢轨中点、中间支承块和桥梁跨中点竖直位移和加速度随刚度的变化

由图9 可知，当扣件竖直刚度增大时，钢轨竖直位移减小，最大可减小52%，支承块位移、轨道和桥梁的竖直加速度都增大而桥梁位移基本不变。这说明扣件刚度不宜过大，否则支撑块的运动受到桥梁的阻碍，与桥梁发生激烈的碰撞而导致支撑块受压破坏;当支承块下胶垫竖直刚度增大时，轨道和桥梁的竖直位移都减小，分别可减小53%、75%和73%，轨道竖直加速度先增大后减小，桥梁加速度一直增大。这说明胶垫刚度也不宜过大，否则会增大桥梁振动，造成桥梁的损坏。

从整体趋势来看，系统部件的位移随刚度增大呈减小的趋势，振动加速度随刚度增大呈增大的趋势。因此，为了取得位移控制和振动控制的平衡点，可以取中间刚度取值，即在40 ～80 kN/mm 之间取值。

5 结论

本文建立了车辆－轨道－桥梁耦合系统的竖直振动矩阵方程，编写了计算车辆－轨道－桥梁竖直耦合振动简化模型的MATLAB 程序，并对程序的有效性进行了算例验证，其结论如下:

1)桥梁的振动频率分布在0 ～200 Hz 的低频段，以一阶弯曲振动为主;轨道的振动频率分布在0～500 Hz 的中低频段，以低于20 Hz 的振动为主。

2)在轨道不平顺的激励下，轮轨冲击力可达轴重的3 倍，是造成轨道结构振动和钢轨损伤破坏的重要原因之一;轨道架设时要对基础进行夯实处理，防止地基沉降变形引起的轨道几何形位的变化，以保证车辆安全、平稳运行。

3)车辆速度的变化对轮轨冲击力和轨道加速度的影响很大，对结构位移的影响很小，高速条件下轨道结构的振动控制和安全维护是重要的研究方向。

4)桥上铺设弹性支承块式无砟轨道时，为减小轨道和桥梁的振动，防止支承块破坏，扣件和支承块下胶垫竖直刚度要相互匹配，刚度宜在40 ～80 kN/mm 之间取值。

［1］张爱莲，陈书剑. ADAMS 柔性体建模技术研究［J］. 煤矿机械，2011(6):95.

［2］晋智斌，强士中，李小珍.高速列车－桥梁竖向随机振动的时域分析方法［J］.地震工程与工程振动，2008(3):110.

［3］张志超，张亚辉，林家浩.车桥耦合系统非平稳随机振动分析的虚拟激励－精细积分法［J］.工程力学，2008(11):197.

［4］逄焕平，董满生，侯超群. 车桥耦合振动分析的状态空间法［J］.合肥工业大学学报:自然科学版，2012(12):1610.

［5］罗文俊，雷晓燕，练松良.车辆－高架桥耦合系统竖向振动分析车辆轨道新模型［J］.华东交通大学学报，2013(2):1.

［6］李东平，王宁波，曾庆元.车桥时变系统耦合振动分析模态综合法［J］.铁道科学与工程学报，2009(3):36.

［7］Vo T P，Lee Jaehong，Ahn N. On sixfold coupled vibrations of thin－walled composite box beams［J］. Composite Structures，2009(89):524.

［8］Nallasivam K，Dutta A，Talukdar S. Dynamic analysis of horizontally curved thin－walled box－girder bridge due to moving vehicle［J］.Shock and Vibration，2007(14):229.

［9］Wu S Q，Law S S. Dynamic analysis of bridge-vehicle system with uncertainties based on the finite element model［J］. Probabilistic Engineering Mechanics，2010(25):425.

［10］翟婉明.车辆轨道耦合动力学［M］. 北京:中国铁道出版社，1997.

［11］王宁波，任伟新，肖祥.列车－桥梁耦合振动研究综述［J］.力学进展，2012(5):634.

［12］Uzzal R U A，Ahmed A K W，Rakheja S. Analysis of pitch plane railway vehicle-track interactions due to single and multiple wheel flats［J］.Proceedings of the Institution of Mechanical Engineers，2009(1):375.

［13］杜宪亭，夏禾，张田.车桥耦合振动迭代求解稳定性研究［J］.振动与冲击，2012(22):62.

［14］Zhua J J，Ahmed K W，Rakhej S，et al. Development of a vehicletrack model assembly and numerical method for simulation of wheel-rail dynamic interaction due to unsupported sleepers［J］.Vehicle System Dynamics: International Journal of Vehicle Mechanics and Mobility，2010(12):1535.

［15］李永乐.风－车－桥系统非线性空间耦合振动研究［D］. 成都:西南交通大学，2003.

［16］Lou Ping，Yu Zhiwu，Au F T K. Rail-bridge coupling element of unequal lengths for analyzing train-track-bridge interaction systems［J］.Applied Mathematical Modelling，2012(36):1395.

［17］李小珍，强士中.列车－桥梁耦合振动研究的现状与发展趋势［J］.铁道学报，2002(5):112.

［18］徐荣桥.结构分析的有限元法与 MATLAB 程序设计［M］. 北京:人民交通出版社，2005.