考虑基础刚度的某步行天桥结构抗震分析

杨必峰 顾 励 张 玉

(悉地(北京)国际设计顾问有限公司，上海200235)

1 引言

传统的建筑结构分析，一般均假设结构在基础受到刚性约束，回避了地基、基础与上部结构之间复杂的相互作用，简化了分析难度。相应地，规范通过基础埋深、地下室的设置、地下室与首层结构的刚度比、顶板厚度等细节与之相匹配，确保了分析结果与实际情况相匹配。

地震下地基与上部结构的共同作用问题，在近30年来获得广泛关注，借助于大型有限元分析软件及振动台试验，在计算分析与试验研究方面有了很大的发展。在建筑结构领域，这方面的研究，主要集中在高层建筑方面。总体而言，考虑了地基影响后，结构的动力特性有所改变，周期变长，阻尼比上升。一些高层建筑的计算分析结果表明，上部结构的地震反应总体呈减小趋势，但也有部分构件内力出现增大。由于基础变形的存在，顶点位移往往大于刚性约束的结果。地基土越软弱，相互作用的影响越显著[1-5]。

对于低矮、抗侧刚度相对较大的结构，目前这方面的研究较少。本文以一座单层板柱剪力墙结构的大型步行天桥为例，对不同基础刚度状态的结构地震反应进行分析对比，以期对同类建筑物的抗震设计提供参考。

2 项目概况

项目位于上海某大型国际度假主题园区，建筑功能为连通各主体场馆的步行天桥。天桥为单层结构，基础面至桥面结构高度为6.5 m。平面呈狭长形的曲线，宽度略大于8 m，东西向长度约150 m，整体不设缝。图1为结构分析模型的示意图。

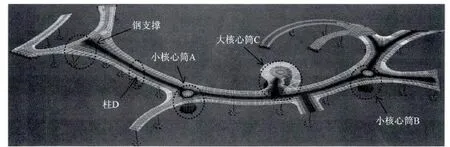
图1 步行天桥结构分析模型示意Fig.1 Analysis model of the foot bridge structure

桥面采用C40现浇混凝土板，中部750 mm厚，两翼300 mm厚。桥面下主要为直径560 mm的钢管柱，布置在桥面纵向中间，整体呈单柱双悬挑的样式。主要的抗侧力构件为三个混凝土核心筒及一道钢支撑。结构体系基本可归结为板柱-抗震墙体系。基础采用柱下或核心筒下独立桩承台。桩采用PHC管桩，桩长42～45 m，以7-2层粉砂为持力层。

结构的抗震设防烈度为7度(0.10 g)，场地特征周期为0.9 s，多遇地震水平地震影响系数最大值为0.08，罕遇地震为0.45。抗震设计性能化要求为:多遇地震下，所有构件保持弹性，钢柱弹性应力比小于0.75，桥面板拉应力小于混凝土抗拉强度标准值;设防地震下，钢柱不屈服，混凝土核心筒及钢支撑保持弹性;罕遇地震下，混凝土核心筒不屈服，钢支撑保持弹性，钢柱允许出现塑性铰但其塑性状态不应达到严重至破坏的程度，桥面板钢筋应力小于屈服强度。

根据建筑造型，整个桥面的典型区段为单柱双悬挑板的形式。如简单的设缝分割为若干规则平面，一方面会严重破坏建筑效果，另一方面各单柱悬挑板区段无法利用核心筒和钢支撑较好的抗侧刚度，也会导致结构的冗余度太低，综合考虑，确定采用整体不设缝的方案。相应地需解决几方面的问题:首先是露天超长结构的温度分析问题[6];其次是不规则结构的抗震分析问题;最后是密集人流下结构的舒适度问题。本文仅就抗震分析方面进行阐述。

与规则的多高层建筑相比，本工程的结构的抗震设计，有很大区别:第一，结构的抗震设计需采用性能化设计方式，明确中、大震下的各部分构件的性能目标，通过弹塑性的分析方法进行检验[7];第二，桥面楼板不再只是一个简单的竖向传力构件，而是作为抗侧力构件的重要部分，需如实考虑面内外刚度，采用弹性的方法进行整体分析;第三，结构的动力特性方面，更类似一个平面内的质量串，而非竖向高度上的一个质量串，地基基础的刚度，会对结构整体的动力特性造成明显的影响。因此，本工程的结构分析，引入了基础刚度，以考虑共同作用的影响。

3 计算模型

结构的分析采用 SAP2000，V15.1中文版。桥面、承台与核心筒采用壳单元，柱与斜撑采用线单元，柱与承台、桥面的连接为固接。

考虑地基与上部结构共同作用的有限元分析，较为精确的方式是将影响范围内的地基土采用实体单元直接建入模型，合理设定土体的弹性模量、质量密度、阻尼比等物理参数，计算容量大，耗时较长。简化的方法可以采用弹簧阻尼的方式，模拟土体对桩承台基础的相互作用，将土体与建筑物脱离，难点在于弹簧刚度与阻尼的取值。对于本文的研究对象，桩土刚度可以通过桩的水平和竖向静载试验数据获得，在此基础上设定出一定的弹簧刚度区间，已能满足工程设计的精度要求。因此，计算分析采用简化的方法，每个承台下桩对应位置设置水平和竖向弹簧来考虑地基的约束，不计桩顶转动弹簧刚度，通过承台下群桩的轴向变形差来模拟柱底的转动变形。分析时偏于保守，不计入弹簧的阻尼。

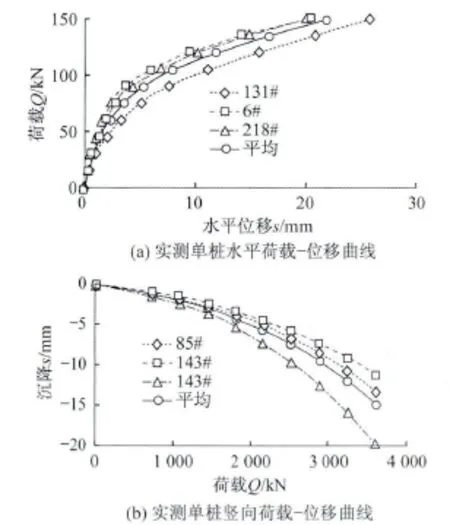
图2 实测单桩荷载-位移曲线Fig.2 Load-displacement curves of the single pile

根据桩的静载实验数据，考虑群桩影响后，小变形状态下，离散到各桩顶的水平和竖向线性弹簧刚度分别为35 000 kN/m和500 000 kN/m。对于大变形状态，例如罕遇地震分析时，可直接给出弹簧的力—变形曲线，以考虑大变形下地基刚度退化的效应。关于桩-土共同作用的等效刚度的具体分析过程和取值可参见文献[6]。图2为实测单桩承载力-位移曲线，实测曲线取平均值后，经文献[6]方法修正，即可作为非线性弹簧输入到模型中。

4 地震静力分析

地震静力分析，采用反应谱方法，主要考察基础刚度变动对结构地震响应的影响，分析时计算振型数取36个。图3给出了嵌固和实测桩基线性刚度下的前6阶振型对比。表1为0.25～1 000倍实测基础刚度以及嵌固状态下，反应谱法的基底剪力。

对比图3可见，考虑共同作用后，结构的各阶振型除局部发生明显振动外，还带动了整个结构的变形，而嵌固条件下，基本上都是局部振动。如观察不同弹簧刚度条件下的振型图，可以发现，随着弹簧刚度的增大，整体振动形态趋弱，局部振动形态渐强，至基础刚度放大100倍以上时，振型与绝对嵌固才比较接近。

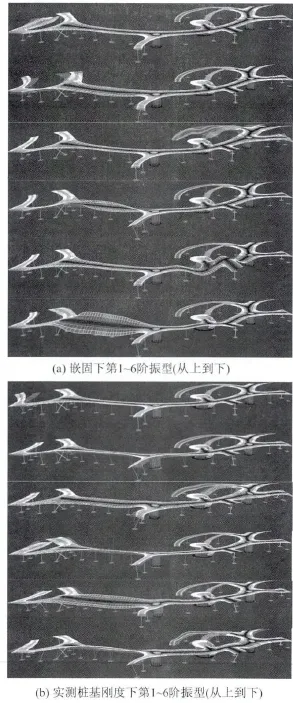
图3 不同约束条件下结构的第1～6阶振型Fig.3 First six vibration modes under different constraint conditions

从表1可以看出，随着支座刚度的增大，结构的第一周期趋向减小，表明整体刚度趋于增大。但整体刚度的增大，并未带来基底剪力的提高，基底剪力反而是呈下降趋势。前10阶振型对基底剪力贡献的比例随着基础刚度的提高不断下降。出现整体刚度提高而地震响应降低的现象，主要原因在于，基础采用弹簧后，整体振型更容易被激发出来，并且随着弹簧刚度的下降，整体振动更充分，低阶振型对地震响应的贡献度大大提高，基底剪力就会更大。这表明考虑桩土共同作用后，既改变了结构的周期，也改变了结构的振型，这是本工程与常规高层建筑考虑桩土共同作用结果的一个显著的区别。

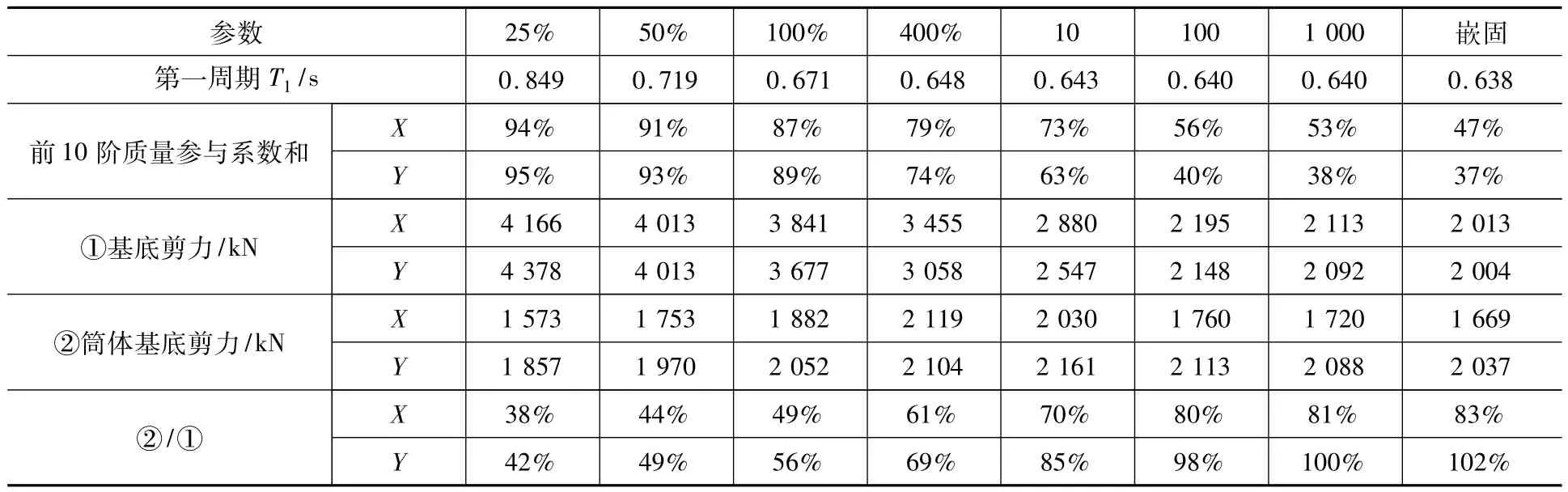
表1 不同支座约束条件下反应谱法输出结果Table 1 Response spectrum analysis results under different constraint conditions

此外，表1也给出了筒体基底剪力与总基底剪力之间的关系。可以看出，筒体的基底剪力随着弹簧刚度的增大而增大，到4～10倍刚度时达到最大值，随后递减，最大值与最小值变动不到10%，筒体承受的剪力基本恒定，新增的基底剪力主要是靠框架柱来承受。筒体基底剪力占总剪力比值，也是随着弹簧刚度减小不断递减的，嵌固时为80%～100%，实测刚度时则下降到50%左右。这反映了筒体与框架柱对基础变形的敏感性是有极大差异的。当基础被绝对嵌固时，由于筒体抗侧刚度比柱子大得多，水平力几乎全部被筒体吸收;而考虑基础弹簧刚度后，核心筒与钢柱之间的刚度差异，由原来的悬殊很大，到相对接近，使得水平力在核心筒与框架之间重新分配，框架所承受的水平力的比例随基础刚度下降不断上升。这是本工程的一个新的特点，如仍按基础嵌固进行抗震分析，将明显地低估框架柱的地震力，有可能导致框架柱在小震阶段即出现破坏，大大降低结构的抗震性能。

5 多遇地震弹性时程分析

多遇地震状态下，采用弹性时程分析的方法，主要考察小震下桥面板应力状态，复核小震反应谱分析结果。

表2给出在实测刚度条件下的小震时程分析结果，时程波采用文献[8]附录的 SHW1，SHW3，SHW4，按1:0.85 双向输入。

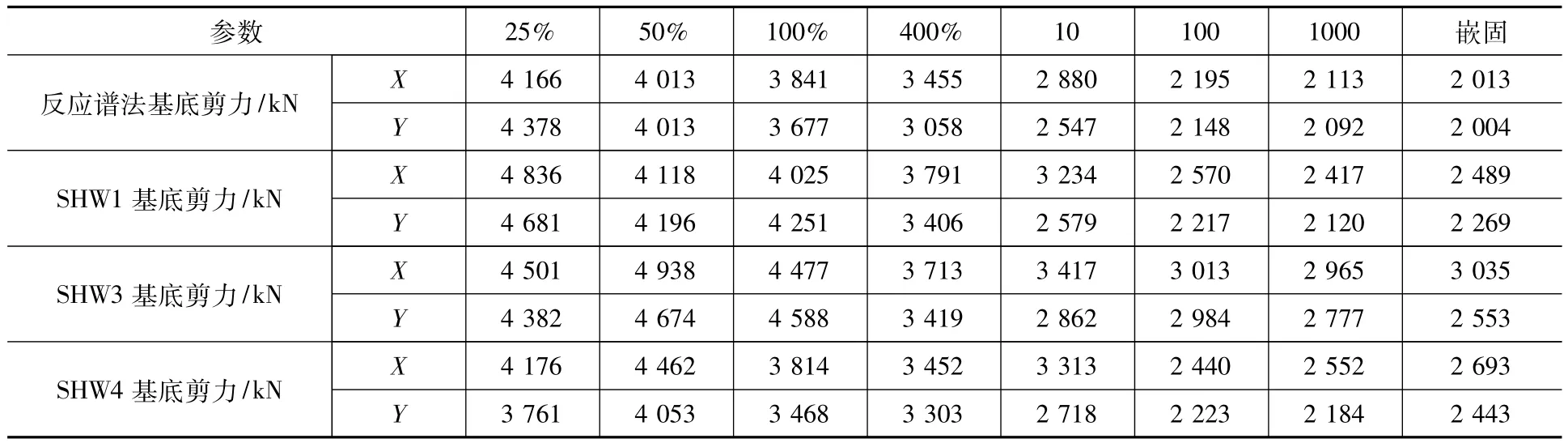
表2 不同支座约束条件下小震弹性时程分析输出结果Table 2 Elastic time history analysis results under frequently occurred earthquakes at different constraint conditions

弹性时程的计算结果，验证了反应谱法的规律，即随着弹簧刚度的增大，结构的地震响应呈减小趋势。另一方面，弹性时程结果普遍比反应谱法来得大，特别是在弹簧刚度大的情况下，偏差很明显。这表明反应谱法在处理低阶振型不占主导的结构，精度偏低，应当采用时程结果加以修正，对反应谱结果做适当得放大。

桥面板是本工程中的重要的抗震构件。由于整个结构的水平力最终需要靠桥面板进行协调，桥面板的性能化要求是小震下板拉应力小于混凝土抗拉强度标准值，大震下板钢筋不屈服，相当于全过程桥面板基本保持弹性状态。考虑到桥面板平面的不规则，高阶振型对桥面板的内力贡献可能比较显著，板的应力分析采用弹性时程的方法，选择地震响应相对较大SHW3波，按1∶0.85进行双向地震输入，并按实测基础刚度条件进行校核。

图4摘录出主要的时程内力最大正值结果。设计时尚应关注内力最大负值结果，取绝对值较大者作为设计依据。图4(a)显示内力峰值集中在板带边缘，表明了桥面板在水平力作用下，平面内弯曲变形为主的特点。最左侧的狭长板带的凹口处内力集中最明显，最大拉力值为882 kN/m。对左侧凹口处最大拉力峰值882 kN/m，取板带平均厚度375 mm，则拉应力值为2.35 MPa，小于桥面C40混凝土抗拉强度标准值2.39 MPa，能满足小震不开裂的要求。

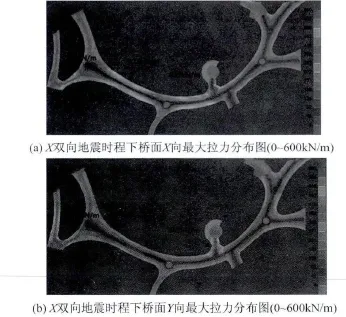
图4 时程SHW3波X双向地震下桥面最大内力分布Fig.4 The maximum internal force distribution from the bidirectional time history analyses under the SHW3 wave

上海地区的大震与小震地面加速度峰值的比值为5.7。对小震的计算结果直接进行放大，可以估算出大震下板的内力状态。仍以凹口处最大拉力峰值为例，取边缘的0.6 m板带布置边缘暗梁，钢筋采用HRB400，强度标准值为400 MPa，则0.6 m宽度内对应所需的配筋面积为7 554 mm2。其他应力集中区域也可按内力大小，设置板带边缘暗梁，根据计算值进行暗梁配筋。

6 罕遇地震弹塑性时程分析

罕遇地震状态下，采用弹塑性时程分析的方法，验证大震下结构的可靠性。此时，基础刚度将明显的退化，结构整体分析时可以通过输入弹簧的承载力-位移曲线，模拟基础刚度的非线性变化。

分析采用的时程波为SHW3波，按1∶0.85进行双向输入，加速度峰值为200 cm/s2。结构的桥面板、核心筒墙体以及基础承台、筏板按弹性考虑，钢柱的柱顶和柱底设置PMM纤维铰。时程分析采用直接积分法，考虑材料和几何非线性影响，考虑弹簧刚度的非线性影响。非线性弹簧的滞回类型采用“Takeda”的方式。分析前，先进行了非线性的重力工况(1.0恒载+0.5活载)的加载。分析比较了以下四种约束方式下的大震时程结果:①固定约束;②25%线性弹簧;③100%线性弹簧;④非线性弹簧。为方便比较，将模型④的加速度峰值调整为小震的35 cm/s2，其余条件不变，作为对比模型⑤。

表3给出了五种模型的输出结果，其中力的单位为kN，位移单位为mm。在线性弹簧条件下，支座刚度越大，总基底剪力越小，筒体剪力占总剪力的比例越大，这和小震下的趋势是一致的。但筒体剪力占总剪力的比重，模型①、②、③分别为33.1%，35.6%，54.2%，明显小于小震下 42% ～100%的计算结果，表明大震下框架的抗侧贡献度是在提高的。

基底的侧向变形主要发生在几个抗侧刚度大的构架上，从表3可以看出，模型①的侧向最大变形达到40～50 mm，模型②的结果相对要小一点。实际上，不论是模型①还是模型②，从图2的结果看，都已经进入荷载-位移曲线的塑性段了，沿用弹性的弹簧刚度，误差是显而易见的。

考虑基础刚度的非线性影响，大震下模型④的基底剪力要明显小于线弹簧模型①、②，甚至小于固定约束模型③。这是因为在大震下，弹簧刚度进入明显的塑性段，在整个桩-土-上部结构体系中，桩-土的塑性变形消耗了大部分地震能量，削弱了整体结构的地震响应。图5为模型④简C基底Y向位移与Y向剪力曲线，从图中可以明显看到基底的塑性变形。模型⑤的Y向基底剪力比表2中100%线性弹簧结果小约24%，表明即使在小震下，位移不大的情况下，基础的非线性效应也一定程度上削弱了上部结构的地震响应。

表3 不同支座约束条件下大震时程输出结果Table 3 Results of rarely occurred earthquake time history analysis under different constraint conditions

图5 模型④筒C基底Y向位移与Y向剪力曲线Fig.5 The Y direction base displacement and shear force curves for the tube C of the model④

观察上部结构的塑性铰分布，模型①、②分别有24根、3根构件进入塑性，占钢柱总量的72.7%和9.1%，模型③、④钢柱均处于弹性状态。模型①、②中，塑性铰最大纤维应变为弹性应变的3.24倍和1.9倍，远未到极限状态。这表明不论在哪种模型条件下，整体结构的抗震承载潜力都较大，但考虑到结构的复杂性和分析采用的相关参数的不确定性，不对构件做截面的优化。

图6为模型①、③、④柱D的顶节点Y向位移时程曲线，柱顶节点的位移已扣除柱底侧移和转角的影响，可以看到不同模型的振动形态差异很大。固定约束状态下，柱的大震响应明显偏小;而考虑基础刚度时，如弹簧刚度设定得偏低的话，又会夸大柱的实际大震响应。

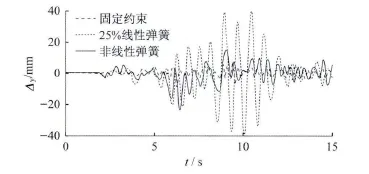
图6 柱D顶节点修正后大震下Y向变形时程曲线Fig.6 Revised Y direction deformation time history curves for the column top under the rarely occurred earthquake

7 结论

(1)对于本例这种单层低矮，平面狭长，结构振动特性呈平面质量串的建筑物，考虑基础刚度对结构的动力特性有明显影响。对此类建筑物的地震分析，可以在实测桩基荷载—位移曲线的基础上，合理设定基础刚度进行整体分析。对于一般的规则建筑物，本例可能并不具有普遍的参考意义。

(2)采用考虑基础刚度的方法进行结构分析，宜比较多种刚度状态，充分评估结构对基础刚度的敏感性，采用包络的方式进行结构的设计。小震状态下的分析可以按线性弹簧方式考虑，大震状态下宜考虑地基基础的非线性刚度影响。

(3)基础的非线性变形会起到耗能作用，削弱上部结构的地震基底剪力。这一点在大震下表现得尤为明显。

(4)框架柱与筒体的抗侧刚度和侧向变形模式差别较大，当二者在结构中同时出现时，考虑基础刚度的整体分析方法会相对弱化筒体抗侧的贡献，提高框架柱的抗侧贡献。简单的沿用基础嵌固的概念，在本例中会导致设计结果偏不安全，不论在小震状态，还是在大震状态，都会明显低估框架柱的抗侧贡献。

[1] 姜忻良，徐炳伟，焦莹，等.大型土-桩-复杂结构振动台模型试验研究[J].土木工程学报，2010，43(10):98-105.Jiang Xinliang，Xu Bingwei，Jiao Ying，et al.Analysis of shaking Table test of large-scale soil-pile-complex structure interaction[J].China Civil Engineering Journal，2010，43(10):98-105.(in Chinese)

[2] 陈清军，姜文辉，楼梦麟，等.群桩基础三维非线性地震反应分析[J].振动与冲击，2003，22(3):98-101.Chen Qingjun，Jiang Wenhui，Lou Menglin，et al.3D nonlinear response analysis of pile group under seismicloading[J].Journal of Vibration and Shock，2003，22(3):98-101.(in Chinese)

[3] 陈建琼，李斌，伍海山，等.土-桩-结构动力相互作用理论研究综述[J].湖南城市学院学报，2006，15(3):9-12.Chen Jianqiong，Li Bing，Wu Haishan，et al.Summary of theoretical research of seismic soil-pile-superstructure interaction[J].Journal of Hunan City University，2006，15(3):9-12.(in Chinese)

[4] 陈素文，严士超.高层建筑-地下室-桩-土系统的相互作用[J].建筑结构，1999，12(12):11-14 Chen Suwen，Yan Shichao.Interaction of tall buildingbasement-pile-soil system[J].Building Structure，1999，12(12):11-14.(in Chinese)

[5] 田堃，朱杰江.基于SAP2000考虑上部结构与基础共同作用的桩基沉降计算研究[J].结构工程师，2015，31(1):99-104.Zhu Jiejiang.Calculation of pile-group foundation settlement considering superstructure and substructure interaction by using SAP2000[J].Structural Engineers，2015，31(1):99-104.(in Chinese)

[6] 杨必峰，张玉，顾励，等.基础刚度对某步行天桥的温度变形的影响[J].建筑结构，2014，44(12):44-47，103 Yang Bifeng，Zhang Yu，Gu Li，et al.Effect of foundation stiffness in temperature analysis of a pedestrian bridge[J].Building Structure，2014，44(12):44-47，103.(in Chinese)

[7] GB 50011-2010建筑抗震设计规范[S].北京:中国建筑工业出版社，2010.GB 50011-2010 Code for seismic design of buildings[S].Beijing:China Architecture ＆ Building Press，2010.(in Chinese)

[8] DGJ 08—9—2013建筑抗震设计规程[S].上海市城乡建设和交通委员会，2013.DGJ 08—9—2013 Code for seismic design of buildings[S].Shanghai urban and rural construstion and traffic committee.Shanghai，2013.(in Chinese)