铁路预应力简支T梁的内力和挠度计算

赵 杰,孙 涛,孙明德

(1.中铁西南科学研究院，四川成都 610031； 2.北京交通大学土木建筑学院,北京 100044)

铁路预应力简支T梁的内力和挠度计算

赵 杰1,孙 涛1,孙明德2

(1.中铁西南科学研究院，四川成都 610031； 2.北京交通大学土木建筑学院,北京 100044)

以32m铁路预应力混凝土简支T梁为研究对象，计算了简支T梁的预应力损失及有效预应力，在传力锚固阶段、空载阶段和使用荷载作用阶段的正应力以及正常运营状态下的挠度。

预应力; 简支;T梁; 计算; 正应力; 挠度

1 工程概况

桥梁为跨度32m的道砟桥面后张法预应力混凝土T型截面梁桥，按照《铁路工程技术规范》第二篇桥涵有关规定进行设计。设计活载为中—活载，梁体如图1、图2所示。

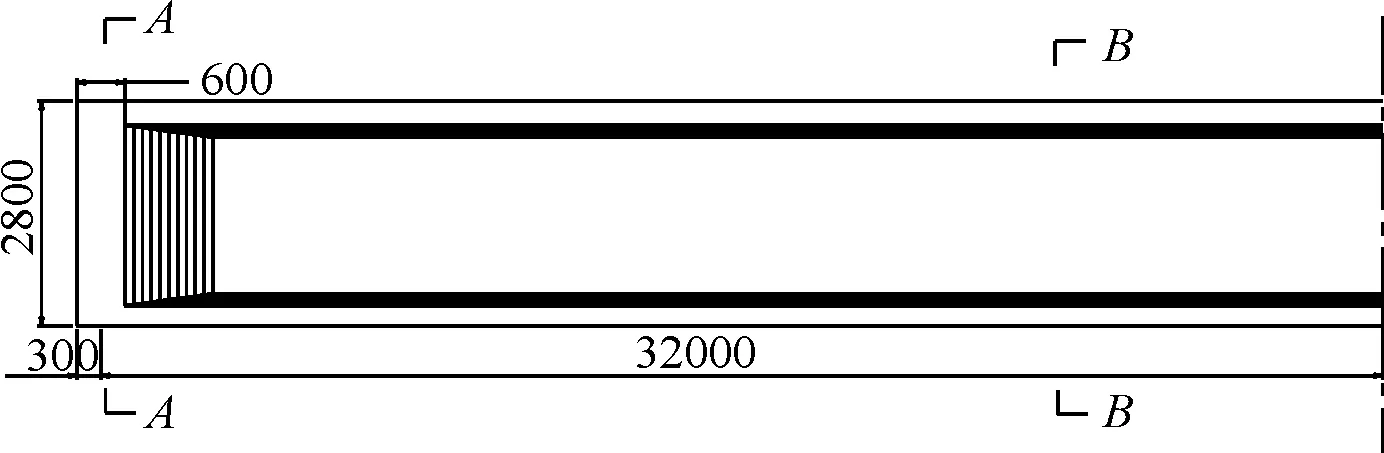
图1 梁体立面(单位：mm)

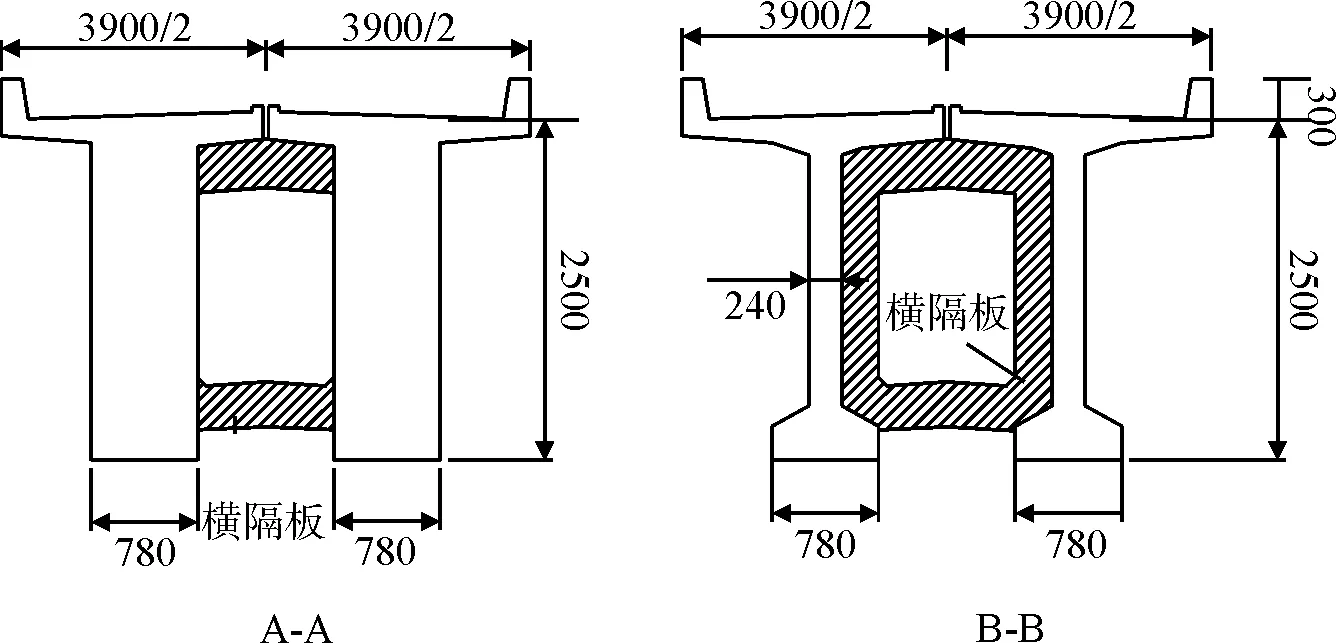
图2 梁体截面(单位：mm)

1.1 材料

混凝土：采用C50混凝土，受压弹性模量Eh=3.5×104MPa。

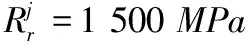
1.2 安全系数

运营荷载作用下，强度安全系数K≥2.0；抗裂安全系数Kf≥1.2。架桥时，强度安全系数K≥1.6；抗裂安全系数Kf≥1.05。

钢丝应力的控制条件参见表1。

混凝土应力的控制条件参见表2。

表2中，Ra、Rl为混凝土的抗拉、抗压极限强度；R为混凝土设计强度。

2 简支梁的计算

简支T梁的计算截面特性参数见表3。

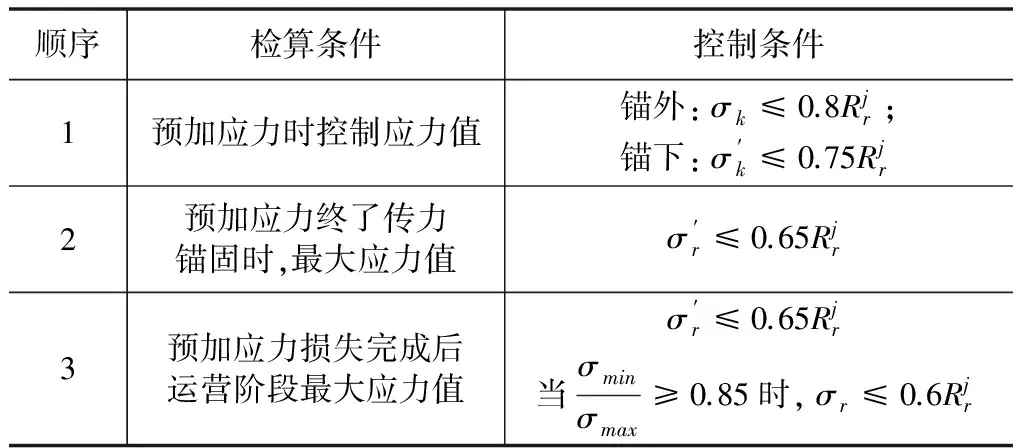
表1 钢丝应力的控制条件

表2 混凝土应力的控制条件

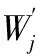
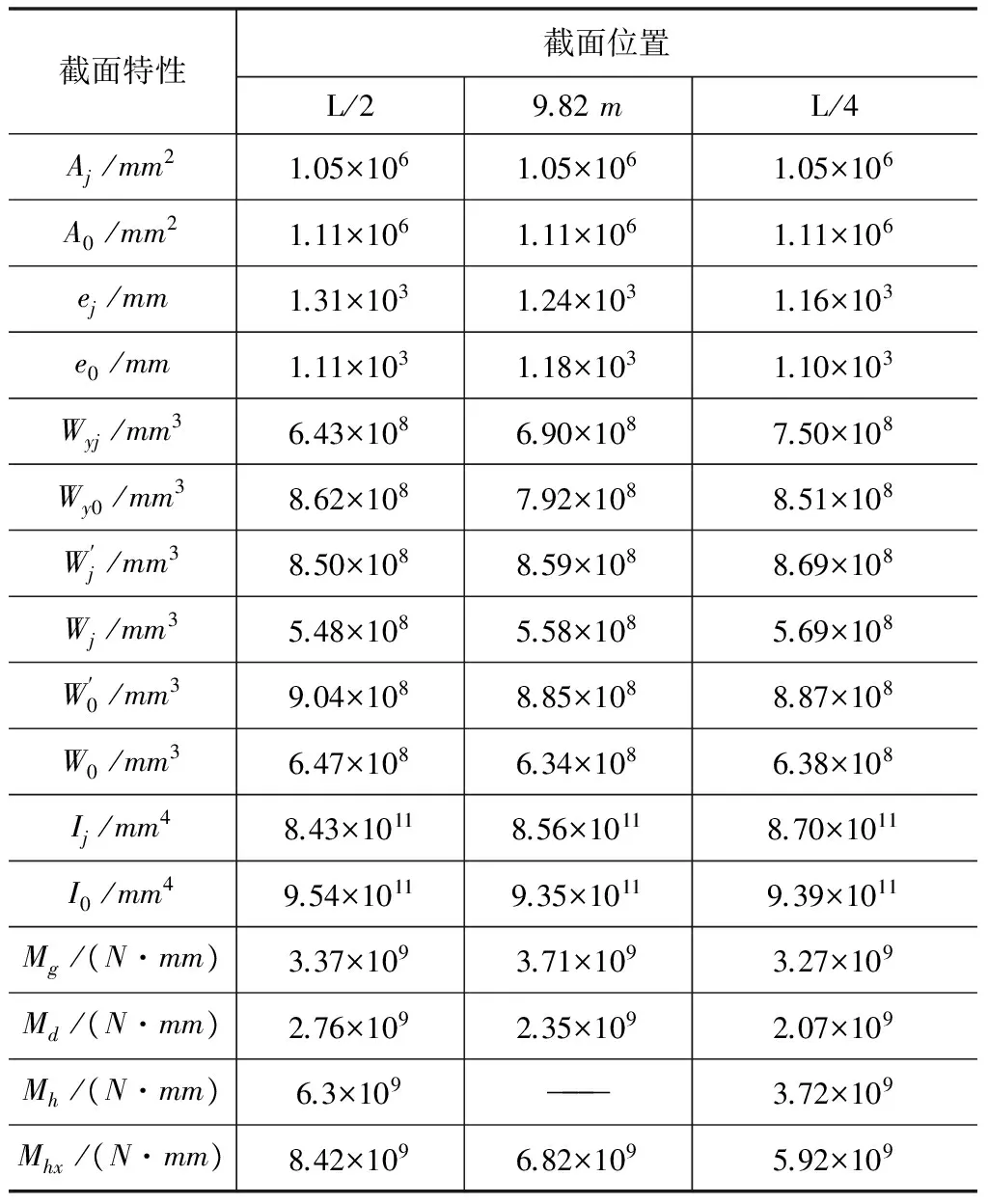
表3 截面特性值

2.1 预应力损失及有效预应力计算

锚头外钢丝束控制应力σk采用图纸设计值1 146.6MPa，即为锚下控制应力。n为钢筋与混凝土的弹性模量比，n=5.714。

各项预应力损失的计算(未注释的参数意义同前)。

2.1.1 由于锚头变形、钢筋回缩和接缝压缩引起的预应力损失σS3

查表得钢制锥形锚头每端钢丝束回缩及锚头变形对跨中的影响为4mm,即ΔL=2×4=8mm,计算钢丝束平均长度L=34 396.4mm。

(1)

式中：ΔL为锚头变形、钢筋回缩和接缝压缩计算值；L为钢丝束平均长度。

2.1.2 由于摩擦引起的损失σS4

(2)

式中：σk为锚下控制应力；θ为从张拉端至计算截面的长度上钢筋弯起角之和；x为从张拉端计算截面的管道长度,可取半跨的平均值；μ为钢筋与管道壁之间的摩擦系数；k为考虑每1m管长对其设计位置的偏差系数。

按灌注混凝土后抽出橡胶管形成孔道，查《桥规》表6.3.4—1得：μ=0.55，k=0.0015。

μθ+kx=0.55×0.11+1.5×10-4×16.2=0.085

查相应规范，内插求得：

σs4=0.081×1.147×103=93.22 MPa

2.1.3 混凝土弹性压缩引起的预应力损失σS6

(3)

式中：N为被张拉力筋根数,值为20；Δσh为在已张拉的力筋的重心处由于后来张拉一批力筋而产生的混凝土正应力。σh=NΔσh，在1/4跨度截面力筋重心处由预加力产生的混凝土正应力。

(4)

式中:Ny为预应力筋产生的预压力，Ny=Ayσycosα；Ay为预应力筋的截面积；σy为预应力筋的预应力。

(5)

式中:cosα为各束钢丝束弯起角度余弦值的平均值。

(6)

将数值代入式(5)、式(6)计算得：

σS6=0.064×944=60.12MPa

σy=944MPa

2.1.4 钢筋松弛引起的预应力损失σS2

σS2=0.08σk=0.08×1.147×103=91.7 MPa

(7)

2.1.5 混凝土收缩和徐变引起的应力损失σS1

(8)

d=2A/μ=236.8mm

式中：A为计算截面面积，A=1 128 600mm2；μ为截面与大气接触的周边长度，μ=9 532mm；σh为取跨中截面和1/4截面钢筋重心处混凝土应力的均值；d为理论厚度。按28d龄期查表得：ε∞=156.4×10-6，φ∞=1.464。

(1)计算跨中截面的σh：

(9)

9.422×103×944×1=8 890kN

(10)

将各数值代入式(9)计算得：

σh=19.8MPa

式中：Ny为力筋对跨中截面混凝土的预压力；Aj为跨中截面净截面面积；Mg为梁自重在跨中截面产生的弯矩。

(2)计算1/4截面的σh：

9.422×103×944×0.998=8 873.2kN

(11)

将各数值代入式(9)计算得：

σh=17.79MPa

式中：Ny为力筋对1/4截面混凝土的预压力；Aj为1/4截面净截面面积；Mg为梁自重在1/4截面产生的弯矩。

(3)平均应力：

σs1= 0.8×(1.56×10-4×2×105+

0.8×5.714×1.464×18.79)=125.63

2.1.6 总的预应力损失σs

(49.4+93.22+60.12)+125.63+91.7=420.07 MPa

(12)

有效预应力σy1：

1.15×103-420.07=726.53 MPa

(13)

2.2 弹性阶段正应力的计算

2.2.1 传力锚固阶段(预加应力阶段)

取跨中截面为计算截面。

(1)预应力与梁自重共同作用下，截面正应力计算(正值为压应力):

(14)

(15)

1.15×103-202.72=943.88 MPa

(16)

将各值代入式(14)、式(15)计算得：

σh=21.77MPa

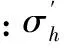
(2)混凝土容许应力值。

预加应力传力锚固或存梁阶段最大压应力值：

预加应力传力锚固或存梁阶段最大拉应力值：

根据计算，σh=21.77MPa<26.25MPa，截面上缘混凝土出现拉应力但满足规范要求。

(3)预应力筋的应力值。

(17)

2.2.2 桥梁空载阶段

(1)应力计算。

在此阶段，预应力损失完成，全部恒载作用下未加活载，压浆前按净截面特性计算，压浆后按换算截面特性计算。对后张法结构，可将预压力Ny分为两部分。

①压浆前的预压力Ny:

(18)

代入数值计算得：Ny=8 461.5kN

②压浆后发生的预应力损失引起的轴向力ΔNy:

(19)

代入数值计算得：

ΔNy=1 615.8kN

(2)跨中截面混凝土正应力。

①上缘混凝土正应力:

(20)

②下缘混凝土正应力:

(21)

代入数值计算得：

σkh=11.82MPa

(3)预应力筋的应力。

(22)

代入数值计算得：

σy=793MPa

式中：σy1为预应力筋的有效预应力；yjy、y0y为计算截面最外排力筋到净截面、换算截面重心轴的距离。

2.2.3 使用荷载作用阶段

计算截面取跨中截面。

(1)计算截面混凝土正应力的计算。

(23)

(24)

代入数值计算得：

σh=0.14MPa

(2)力筋中的应力计算。

(25)

代入数值计算得：

σy=856.42MPa

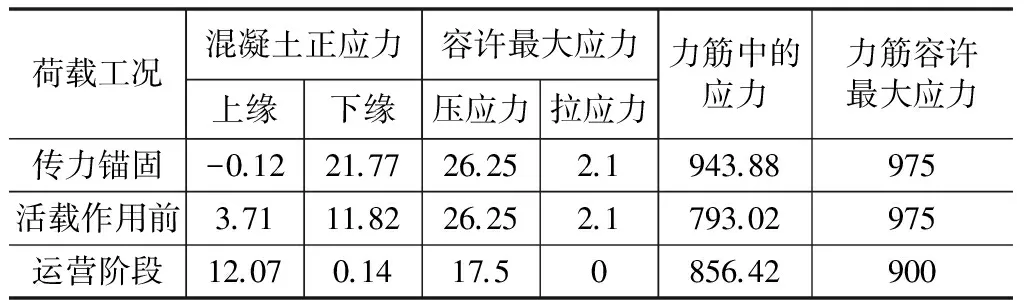
表4 加固前弹性阶段应力 MPa

2.3 变形计算

2.3.1 预加应力产生的上拱度fy

(1)传力锚固时的上拱度fyi。

梁内预应力筋布置形式为偏移抛物线。

(26)

代入数值计算得：

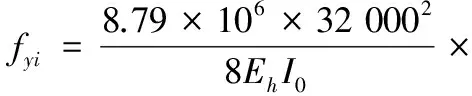
(2)预应力损失引起的挠度变化Δfy1。

(27)

(3)由混凝土徐变引起的挠度变化Δfy2。

(28)

式中：φk为混凝土徐变特性的终极值，取2.0。

(4)预应力产生的上拱度fy。

fy=-37.64+7.84-68.54=-98.34mm

2.3.2 构件自重产生的挠度fg及其他恒载产生的挠度fd

考虑混凝土徐变影响后，其跨中挠度分别为：

(31)

代入数值计算得：

fg=51.7mm

fd=32.7mm

2.3.3 活载产生的挠度fH

(32)

2.3.4 运营荷载作用下的总挠度

-98.34+51.7+32.1+20.1=5.56 mm

(33)

挠度计算结果见表5所示。

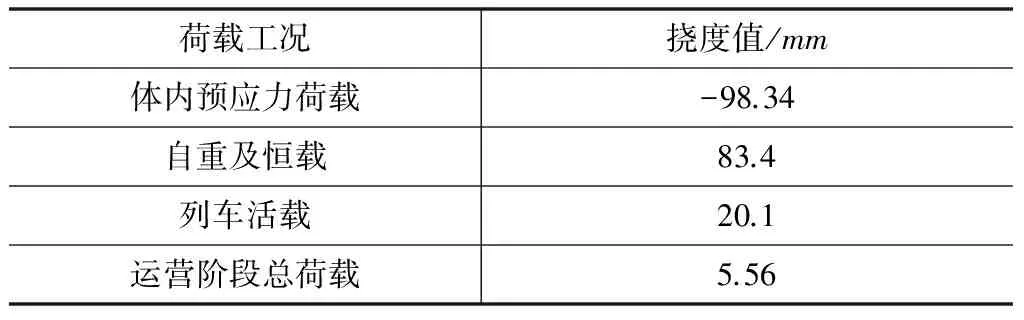
表5 挠度计算结果

根据《桥规》要求，铁路预应力混凝土简支梁桥在正常运营状态下，梁的挠度f

3 结论

通过对32m铁路预应力混凝土简支T梁各工作阶段的受力分析与计算，弹性阶段的混凝土应力均满足设计要求，铁路预应力混凝土简支梁桥在正常运营状态下，梁的挠度也满足设计要求。

[1]TB10002.1-2005铁路桥涵设计基本规范[S]

[2] 熊学玉，蒋志贤．预应力摩擦损失的合理设计建议[J]．结构工程师，1997,(4)

赵杰，女，工程师，从事地铁设计；孙涛，男，工程师，从事桥梁检测和加固；孙明德，男，学生，从事桥梁基本理论研究。

TU378.2

B

[定稿日期]2014-09-23