利用VTK实现几何模型的三维建模

陈小艳，王 强，2，李柏林

（1.西南交通大学 机械工程学院，成都 610031；2. 成都工业学院 机械系，成都 610031）

利用VTK实现几何模型的三维建模

陈小艳1，王 强1，2，李柏林1

（1.西南交通大学 机械工程学院，成都 610031；2. 成都工业学院 机械系，成都 610031）

针对钢结构桥梁的三维可视化问题，提出利用VTK的三维建模功能，同时利用C#语言实现了钢结构桥梁的节点单元数据的三维可视化。研究VTK的数据表达方式，实现模型的拉伸、旋转等建模；结合四元数法，实现模型的旋转几何变换。实验结果表明，通过VTK实现钢结构桥梁节点单元数据三维建模是可行的；该可视化平台具有很好的可移植性和扩展性，并且可以方便的依靠底层数据对模型进行有限元分析等开发工作。

三维可视化； VTK；三维建模； C#语言；四元数

在传统工程行业如机械、土木、电气等方面，二维图纸的表达已经不能满足现在工程的需要，目前，大部分企业都有自己的三维可视化部门，以解决二维图纸带来的缺陷和不足[1]。三维可视化是其它功能如分析、仿真等功能的实现基础。目前，国内外实现三维可视化的技术主要包括以下几种方法。

（1）直接在现有三维软件上进行建模，如CATIA、UG、PRO/E等；或者以这些软件为基础进行二次开发来实现专用需求。采用这种方法能够方便的实现三维可视化，这种方式目前应用比较广泛。设计人员不必关心图形可视化的内部实现算法，可以把更多的精力集中在设计上。但是这些模型只能依附于各自的软件系统来展示模型，由于模型格式解读比较困难，如果想将三维模型嵌入用户自己的软件系统中实现别的相关的需求是非常难于实现的。

（2）在现有的三维引擎上进行开发，比如Open-GL。这种方法能够实现各种三维模型的可视化显示，而且与平台无关，可以在任何软件系统中实现三维可视化。这类方法由于开发工作量比较大，对于开发人员的专业要求比较高，在实际应用中也比较难实现。

本文采用一种C#语言和VTK结合进行开发的方法，实现了钢结构桥梁的三维可视化显示。由于C#语言是完全面向对象的，使用起来非常方便。在开发过程中不用担心内存管理，系统稳定性较好。VTK是在OpenGL的基础上建立的一套函数库，以其强大的三维可视化功能及易用性而受到欢迎。由于开发环境的便利性，使得开发的效率得到了提高。

1 VTK简介

VTK(Visualization Toolkit)是由William J. Schmeder, Kenneth M.Martin, William E. Iorensen三人于1993年开发，利用面向对象的技术设计和实现的三维可视化工具箱[2]。最早主要用于医学图像可视化。目前除了在医学可视化上的广泛应用外，也加入了几何图形的三维建模功能。著名的分析软件MIDAS就是基于VTK开发实现的。然而，国内却很少有人知道VTK的三维建模功能。导致很多应用不得不买国外的软件来实现。VTK包含了三维计算机图形学、图像处理和可视化3部分功能。其中封装了目前许多优秀的三维可视化算法，可以方便的实现数据的三维可视化[3]。

VTK建立在OpenGL基础之上，与平台无关。它不仅支持对几何的显示及渲染，同时支持多种图形算法（光栅图形生成算法，消隐算法等）、可视化算法（矢量，标量，张量） 及高级的建模技术（快速建模，多边形优化，Delanay 三角面片生成法）。而且，VTK 的开发者组织了一个有效的论坛及新闻组，通过这种平台，VTK 的使用者之间可以方便地进行交流与合作[4]。

可视化模式由数据对象和处理对象组成。在VTK中，主要有5种数据集类型：结构化点集（Structured Points）、线性网格（VTKRectilinear Grid）、结构化网格（Stucturedd Grid）、非结构化网格（Unstructured Grid）以及多边形数据（Polygonal Data）[5]。处理对象主要包括数据源对象、过滤器以及映射器。VTK的可视化过程是基于管线流的设计模式。将要处理的数据作为流动介质在管线中流动，不同的阶段对数据有不同的处理方式[6]。 VTK的可视化流程如图1所示。

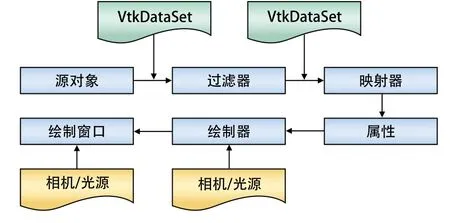
图1 VTK可视化流程

可视化模型主要对数据进行处理，生成可被绘制的集合体，而图形模型主要对生成的几何体进行绘制。有了可视化管线，VTK的可视化过程就可以用数据在可视化管线流动的过程来描述。

在C#语言中使用VTK是使用基于VTK的.net封装包.net Wrappers for VTK。这是一个开源的软件包，可以在VTK的网站上直接下载来使用。基于C#语言的VTK开发效率要比基于C++语言的VTK开发效率高很多，主要表现在以下几个方面：

（1）由于Form编程代替了MFC的界面编程，界面设计只需要使用相应的控件，使得更方便的搭建应用程序框架；

（2）由于C#语言的垃圾回收机制，使得进行对象生成和销毁管理更加方便；

（3）VTK的.net 封装使得VTK的引用更加方便，只需要使“using vtk”,就完成了在C++语言中的所有头文件的引用；

（4）由于采用的C# Form编程，使得窗口消息的获取更加方便；

（5）C#语言是完全面向对象的，使得对程序的设计实现和管理更加方便。

2 基于VTK的三维可视化平台设计

2.1 可视化平台数据存储和管理

几何模型是由点、线、面和体组成。其中，点是组成所有几何模型的基础。因此，所有数据存储的基础都是基于点的存储。在本可视化系统中，点的数据存储采用C#语言的字典类（directory（TKey，TValue））来实现。Dictionary（TKey，TValue）类在内部是作为一个哈希表来实现的，它提供了从一组键到一组值的映射，通过键来检索值的速度是非常快的。因此，可以方便的实现点的操作如添加、删除、修改等。TKey表示点的ID，TValue表示点的3D坐标。在实际应用中添加点用如下代码所示：

//声明一个点存储字典

Dictionary〈int, Point3D＞ pointList =

new Dictionary〈int, Point3D＞();

//声明一个3D点变量

Point3D pointCoor = new Point3D();

//对点进行坐标赋值

pointCoor.x = x;

pointCoor.y = y;

pointCoor.z = z;

//将点添加到字典中

pointList.Add(pointID, pointCoor);

有了点的存储基础，线和面以及体的存储就比较方便，其存储方式都采用字典类来实现。其中，线的存储采用与点关联的方式，面的存储采用与线关联，体的存储采用与面关联。在字典中存储线的格式Directory(lineID,List〈pointID＞)，存储面的格式Directory(faceID,List〈lineID＞)，存储体的格式Directory(bodyID,List〈faceID＞)。

对于点、线、面以及体的操作主要包括添加、删除和修改等。（1）对体的操作，由于体处在最顶层，如果添加一个体，根据构成体的对应面直接生成；如果删除体，则直接删除体而保留对应的面数据。如果修改体，则根据对应的面数据重新生成体。（2）对于其他3类数据点、线和面的操作，由于每一类的操作都关联了另一类数据，如果是添加操作，因为添加不与已经存在的数据相关联，则直接生成新的数据；如果是删除或修改，则提示用户是否保留其下一层数据。如果删除线，则提示用户相关联的面和体数据是否保留。

2.2 可视化平台的三维模型生成

三维建模方法总结起来主要有以下几类：拉伸、旋转、扫描以及螺旋扫描等。几乎所有三维模型都是由这些基本的命令组合生成。拉伸是指一个二维截面图形沿着指定方向运动生成实体；旋转是指二维截面沿着指定轴旋转生成实体；扫描指截面沿着指定路径运动生成实体；螺旋扫描指截面沿着指定路径运动的同时绕指定轴旋转而生成的实体。

在实际建模中，根据实体特征构建二维截面，然后根据特征类型选择不同的三维生成方法。比如拉伸特征的创建：（1）在字典类中查询构成二维截面的线ID；（2）根据线ID查询点的ID；（3）得到点的坐标。根据点的坐标依次连接成二维截面。同时，根据点坐标计算拉伸方向，拉伸方向为二维截面的法线方向。在创建拉伸特征的时候，有两个问题需要解决：点的连接顺序，拉伸方向的计算。在本系统中，结合钢结构桥梁可视化的特点：根据用户输入的点和单元，可视化杆系单元，定义杆系单元的截面类型，根据截面类型来确定点的连接顺序。截面的拉伸方向为法向，法向计算根据点坐标来完成。

设：A(x1, y1, z1)，B(x2, y2, z2)，C(x3, y3, z3)是平面上的3个点，这3个点可以形成3个向量。

AB(x2-x1, y2-y1, z2-z1)，

AC(x3-x1, y3-y1, z3-z1)，

BC(x3-x2, y3-y2, z3-z2)，

取向量AB和BC做叉积AB•BC，利用三阶行列式，写成：

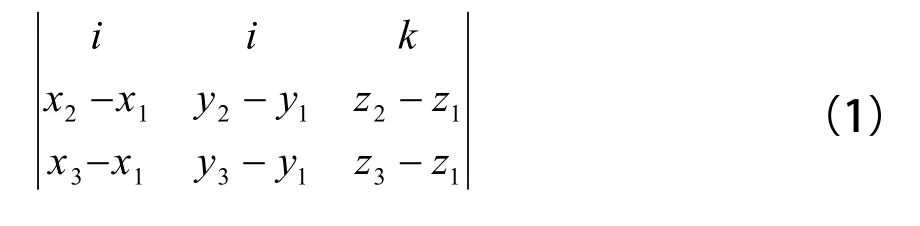
计算行列式即解出平面法向量的坐标，其方向满足右手螺旋法则。图2是生成的工字钢的拉伸三维模型。关键代码如下：

//构建二维截面数据

vtkPolyData pPolyData = new vtkPolyData()

pPolyData.SetPoints(pPoints);

//创建拉伸

vtkLinearExtrusionFilter extrude = new

vtkLinear-ExtrusionFilter();

//设置拉伸截面

extrude.SetInput(pPolyData);

//设置拉伸长度

extrude.SetScaleFactor(iDis);

//设置拉伸方向

extrude.SetVector(direcX,direcY,direcZ);

图2 拉伸成型的工字钢三维模型

2.3 模型三维几何变换

几何变换主要包括平移、旋转等操作。对于相同的模型，不需要进行重复建模，只需要将模型平移或旋转到相应的位置即可。平移操作只需要进行坐标平移操作，相对比较简单，这里不再详述。三维空间的旋转变换可采用欧拉角、几何旋转矩阵或者四元数等方法。欧拉角存在万向节死锁，即当3个万向节其中两个轴发生重合时，会失去一个自由度，而采用旋转矩阵需要大量的乘法运算。因此，本文采用四元数法实现模型的任意方向旋转，四元数（Quaternions）是由爱尔兰数学家威廉・卢云・哈密顿 (William Rowan Hamilton）在1843年发明的数学概念。四元数的乘法不符合交换律，它是最简单的超复数，非零四元数的乘法群在R3的实部为零的部分上的共轭作用可以实现转动。单位四元数（绝对值为1的四元数）若实部为cos(t)，它的共轭作用是一个角度为2t的转动，转轴为虚部的方向[7～10]。四元数的优点是：

（1）表达式无奇点（和例如欧拉角之类的表示相比）；

（2）比矩阵更简炼，也更快速；

（3）单位四元数的对可以表示四维空间中的一个转动。

设空间任意向量A(xa, ya, za)与一旋转角度θ，如图3所示：

图3 四元数旋转示意图

将之转换为四元数：

对于三维空间的任意轴旋转，假设有一向量P(x, y, z)，对一单位四元数q做旋转，将P视为无标量的四元数Xi+Yj+Zk，则向量的旋转经证明如下：Rot(P)=qpq-1。为了计算方便，用矩阵的方式来表示四元数的乘法，假设四元数表示如下：q=[w, x, y, z]=[s,v]，其中s=w是标量部分，v=(x, y, z)是矢量部分。两个四元数相乘的矩阵表示法如下：

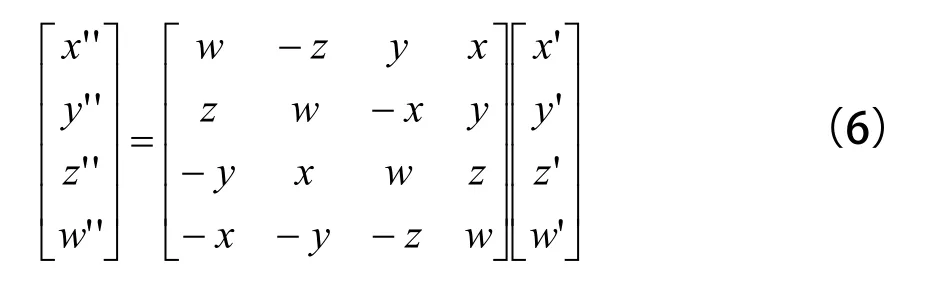
令 q=[s,v]=[cosθ, u☒sinθ]其中u为单位向量，则可以证明q☒q'☒q-1会让q'绕着u轴旋转2θ，此即为四元数的旋转公式。根据四元数的矩阵乘法和旋转，将旋转公式用以下矩阵的乘法来表示：

也就是说如果要让任意向量(x', y', z') (w'为0)对某个单位向量轴u(x, y, z)旋转角度2θ，则w=cosθ，代入以上的矩阵乘法，即可得旋转后的(x'', y'', z'')，为了方便，转换矩阵的最下列与最右行可以省略不写。利用上式变换矩阵。即可实现三维模型的任意方向的旋转变换。

3 三维可视化实例

如图4是采用VTK和C#语言结合开发的钢结构桥梁的三维可视化平台。通过数据导入将桥梁结构的点数据和单元数据导入系统，定义单元的截面形状，最后通过VTK的三维建模功能以及四元数法实现模型的几何变换后实现的整个钢结构桥梁的三维可视化显示结果。图中定义的截面形状为工字型截面。点数据共有577个，单元数据共有937个。钢结构桥梁的三维可视平台如图4所示。图4（a）是节点和单元的杆系结构可视化；图4（b）是将单元进行三维渲染的结构；图4（c）是定义单元的截面形状；图4（d）是图4（b）三维可视化的局部放大图。实验表明，通过VTK实现三维建模是可行的。

4 结束语

VTK作为一种可视化工具包，主要用于医学图像的三维重建。本文利用VTK和C#语言开发工具，提出了在VTK中进行几何实体的三维建模方法。采用C#语言的directory类进行数据存储和管理；对于大数据量的几何变换操作，利用四元数法的旋转，减少了模型在任意方向旋转的时间。实验证明，采用VTK和C#语言结合的方式，可以方便快速地实现几何模型的三维建模，开发效率较高，并且不受系统限制，可以在用户自己的平台上实现三维建模。在实际工程应用中具有较强的应用价值。

图4 钢结构桥梁的三维可视化平台

[1]张祖勋，郑顺义，张剑清.三维可视化工程设计的研究[J].武汉大学学报：信息科学版，2002，27（4）：337-342.

[2]A.C.Pavao. E.V.S.Pouzada, M.A.Mathias. Electromagnetic field visualization through vtk software[C]. Microwave and Optoelectronics Conference, 2001. IMOC 2001, Belem, Brazi, Proceedings of the 2001 SBMO/IEEE MTT-S International, 2001,21-24.

[3]王延华，洪 飞，吴恩华. 基于VTK库的医学图像处理子系统设计和实现[J].计算机工程与应用，2003，39（8）：205-207.

[4]Cline H, Lorensen Wetal. Two algorithm for three-Dimensional reconstruction of tomograms[J]. Medical Physics,1988,15(3): 320.

[5]William J. Schroeder, Lisa S. Avila, Kenneth M. Martin. The visualization toolkit user's guide[M].GE Corporate Research & Development,2001: 89-117.

[6]Arjan J.F. Kok, Robert van Liere. A multimodal virtual reality interface for 3D interaction with vtk[J]. Knowledge and Information Systems, 2007(13): 197-219.

[7]王 勇，马立元，王忠强.四元数法在计算机图形中的应用[J].军械工程学院学报，2001，13（2）：48-51.

[8]刘俊峰.三维转动的四元数表述[J]. 大学物理，2004，23（4）：39-43.

[9]Pletinckx D. Quaternion calculus as a basic tool in computer graphics[J]. The Visual Computer,1989, 5 (1) : 2-13 .

[10]刘爱东,黄 彬,卢中武.基于四元数的坐标旋转与插值方法研究[J]. 计算机与现代化，2012，27（2）：44-47.

责任编辑 徐侃春

3-D modeling for geometric model through VTK

CHEN Xiaoyan1, WANG Qiang1,2, LI Bailin1
( 1.School of Mechanical Engineering, Southwest Jiaotong University, Chengdu 610031, China; 2. Department of Mechanics, Chengdu Technological University, Chengdu 610031, China )

A 3-D modeling method, taken advantage of VTK, combined with C#, was proposed to solve the 3-D visualizing problem of steel structure bridges. Data expression of VTK was researched, geometric transformations of model such as stretching, rotation were implemented through VTK and quaternion algorithm. Experiment showed it was practical to implement 3-D model building via VTK. In addition, the visualization platform was with portability and expansibility, fi nite analysis for model was available with underlying data.

3-D visualization; VTK(visualized toolkit); 3-D modeling; C#; quaternion

U242.5∶TP39

A

1005-8451（2015）07-0007-05

2014-12-01

四川省科技支撑计划（2013GZ0032）。

陈小艳，在读硕士研究生；王 强，在读博士研究生。