基于MFAC的快速路主辅路的均衡控制

程志辉，金尚泰

( 北京交通大学 先进控制系统实验室，北京 100044)

基于MFAC的快速路主辅路的均衡控制

程志辉，金尚泰

( 北京交通大学 先进控制系统实验室，北京 100044)

为了解决快速路主辅路交通密度不均衡造成的局部道路拥挤和资源浪费现象，本文提出了基于无模型自适应控制的快速路主辅路均衡控制方法，该方法中引入了均衡控制思想中的差值控制方法，该方法不受入口匝道和辅路交叉口的模型限制，利用入口匝道流率与交叉口离驶率输入数据和主辅路路段密度输出数据，即可实现强非线性快速路主辅路系统的无模型自适应控制，使主辅路达到系统级的密度均衡。Matlab平台上的仿真比较结果表明了这种控制方法的有效性。

无模型自适应控制；均衡控制；入口匝道；交叉口

目前，学者们对快速路的控制方法做了很多研究，也取得了很多有效的成果，主要有匝道控制，主线控制和通道控制，匝道控制中的入口匝道控制方法[1～2]是在快速路主路的控制中应用最广的，主要的控制算法有占有率控制法，交通需求-通行能力控制法、最优控制法、积分反馈控制法、线性二次型反馈控制法、智能控制法等。其中包括模糊控制和神经网络控制等。当前ALINEA控制[3]是应用最广泛的，它属于积分反馈控制。

从快速路的控制方法中看，常用的入口匝道控制中的ALINEA控制对于具有强非线性、时变、结构及参数不确定的系统控制效果不好，没有理论分析结果保证其稳定性，意味着当交通系统的结构或参数发生变化时，ALINEA很难保证控制品质，而在交通系统这样的复杂系统中，外界因素会使其结构或参数发生变化，如天气变化，交通事故等[4]。辅路交叉口控制中的定时控制无法应对实时变化的交通流，对于强非线性的交通系统，其控制效果也不好。

因此，本文把快速路系统和辅路系统看成一个多入多出的系统，称为快速路主辅路系统。为了能适应具有强非线性的快速路主辅路系统，本文引入无模型自适应控制方法（MFAC）[5～6]，为了能同时考虑主路和辅路，均衡主辅路的交通流，本文引入差值控制方法[7]，通过对多个入口匝道和多个辅路交叉口的集成控制，动态均衡的分配主辅路上的交通流，使快速路主辅路达到系统级的密度均衡。

1 快速路主辅路系统模型

1.1 主辅路路段划分

本文从宏观上研究主辅路的交通流分配，研究对象为一条包含多个路段的单向单车道的快速路主辅路系统，如图1所示。该段快速路包含若干个进出口匝道和若干个辅路交叉口，图中箭头方向表示车流方向，虚线部分表示快速路与辅路交叉口的立体交叉路段。为便于建模本文将这段快速路划分为若干个路段。每个路段最多包含一个入口匝道，一个出口匝道和一个辅路交叉。

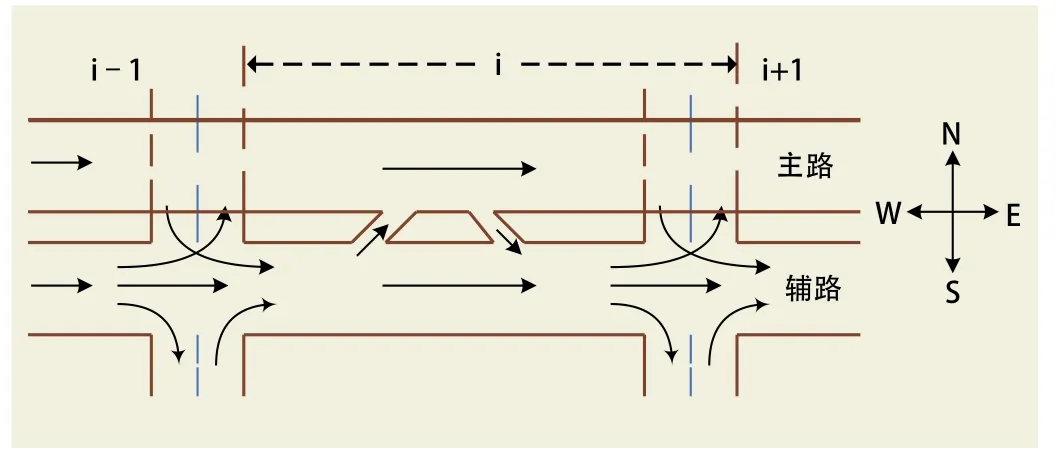
图1 路段划分

1.2 主路交通流模型

主路交通流是连续交通流，Papageorgiou于1989年提出的离散宏观交通流模型[8]在快速路主路的交通仿真研究中已得到广泛应用，该模型是时空离散模型，其数学描述如下：

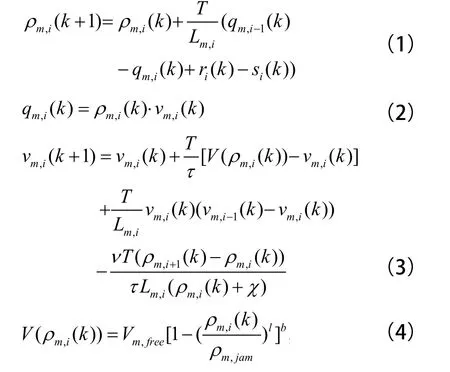
式中T是采样周期（h），k={0, 1, …, K}表示第k个采样间隔，i={1, …, n}表示第i个快速路路段，n表示路段的总数，下标m表示主路路段。模型变量的含义如下。ρm,i(k)：主路路段i在第k时段的平均密度（veh/lane/km）；vm,i(k)：主路路段i在第k时段的平均速度（km/h）；qm,i(k)：第k时段从i路段到i+1路段的平均流量（veh/h）；ri(k)：第k时段从入口匝道i进入主路的车流率(veh/h)；Si(k)：第k时段从出口匝道i进入辅路的车流率(veh/h)；Lm,i：主路路段i的长度(km)；Vm,free和ρm.iam分别表示主路的自由流速和最大密度；v, τ, χ, l, b是常参数，反映特定交通系统的道路几何特点、车辆特征、驾驶员行为等。边界条件如下：

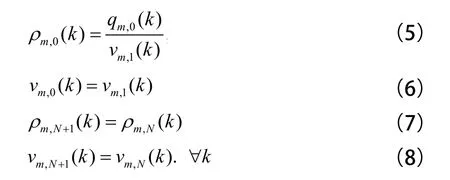
1.3 辅路交通流模型

辅路交叉口的存在使得辅路交通流为间断交通流，本文考虑使用在交叉口建模中应用比较广泛的存储转发模型（Store-and-Forward Model）[9～10]来建立辅路交通流模型。本文考虑的是两相位交叉口，东西方向车流是第1相位，南北方向车流是第2相位，不考虑损失时间，其数学描述如下：

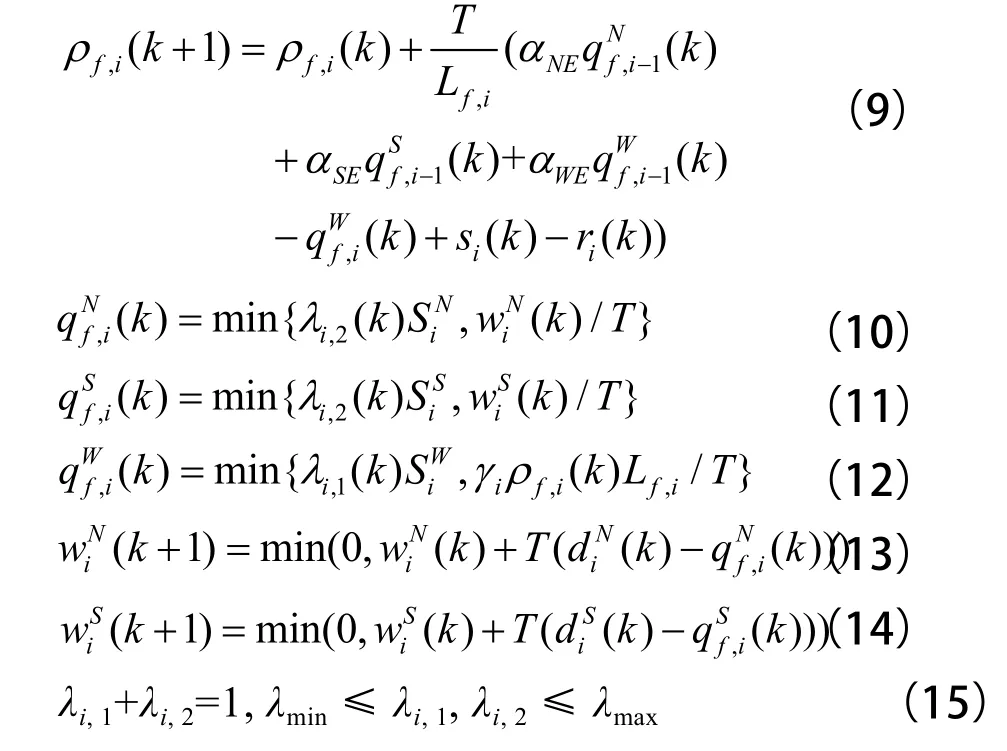
式中变量的含义如下，ρf,i(k)：第k 时刻辅路路段i的密度（veh/lane/km）； qWf,i(k)，qSf,i(k)，qNf,i(k)：第k时段交叉口i西侧、南侧和北侧的车辆离驶率（veh/h）；wSi(k)，wNi(k)： 第k时段交叉口i南侧和北侧的车辆排队长度（veh）；λi,1(k)，λi,2(k)：第k时段交叉口i第1相位和第2相位的绿信比；dSi(k)，dNi(k)：第k时段交叉口i南侧和北侧的车辆到达率（veh/h）； SWi，SSi，SNi：交叉口i西侧、南侧和北侧道路的饱和流率（veh/h）；αWE，αSE，αNE：分别表示交叉口处从西向东，从南向东，北向东的车流转弯比例； γi：在一个采样周期内，车辆行驶的最长距离占辅路路段i的比例。

2 基于MFAC的快速路主辅路的均衡控制

2.1 无模型自适应控制

无模型自适应控制（MFAC，Model free adaptive control）是由侯忠生教授提出的[5]，其主要思想是把非线性系统转化成动态线性化数据模型，动态线性化的方法及推导过程见文献[6]。MFAC控制仅依赖受控系统的I/O数据，不受任何控制对象模型信息的限制，能够实现未知受控系统的参数自适应控制和结构自适应控制。目前，MFAC方法已经在电机[11]、交通控制[4～12]、温度[13]、化工、风力发电[14]、工程结构减震、人工心脏心率调节等领域中得到成功的应用。理论分析，仿真研究和实际应用均表明MFAC方法简单实用，计算负担小，易于实现且鲁棒性强，能够处理未知非线性时变系统的控制问题。文献[4]和文献[12]中已经证明了MFAC在非线性时变的快速路系统中有较好的控制效果，因此在快速路主辅路系统中，本文引入MFAC控制方法。

2.2 控制目标

均衡控制目标包括两部分：(1)以入口匝道处主辅路路段密度差为控制目标，通过对入口匝道流率的控制使主辅路密度差跟踪到期望主辅路密度差，达到主辅路密度均衡的效果；(2)以辅路密度和相邻辅路路段的密度差为控制目标，通过对交叉口流率的控制使辅路密度跟踪到期望密度，并使相邻辅路路段之间的密度差异最小。通过以上两部分的协调控制便可动态均衡的分配主辅路中的交通流，使主辅路密度在整个系统上达到均衡。

2.3 基于MFAC的快速路主辅路的均衡控制算法

本文把主辅路系统看成是多输入多输出的非线性系统，综合考虑入口匝道和交叉口的交通流在主辅路系统中的耦合关系，把两部分均衡控制集成到一个控制器中，提出了基于MFAC的快速路主辅路的均衡控制算法，该算法不依赖入口匝道和交叉口的模型信息，仅利用主辅路系统的I/O数据即可实现无模型自适应控制。这里直接给出基于MFAC的快速路主辅路的均衡控制算法：

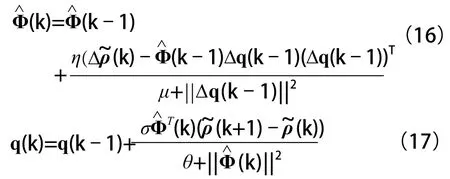
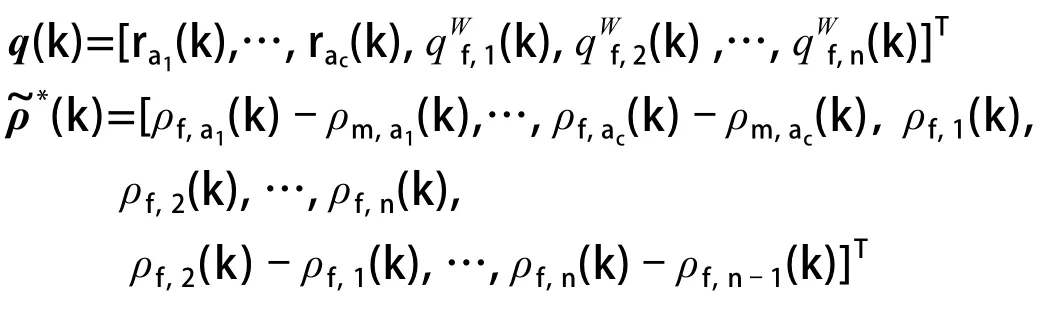
3 仿真分析

为了验证本文提出的控制算法的有效性，这里给出两种情况的仿真比较。情况1：入口匝道无控制，辅路交叉口采用定时控制。情况2：采用基于MFAC的快速路主辅路的均衡控制。

仿真路段考虑一段主辅路均为单车道的快速路，车流为从西向东，长度为6 km，分为12个路段，每段长为0. 5 km，即 Lm,i=Lf,i=0.5 km，主路交通流模型中的参数如下： ρm,jam=80 veh/lane/km， vm,free=80 km/h，l=1.8，b=1.7，χ=13 veh/km，τ=0.01 h，υ=35 km2/h。辅路交通流模型中的参数如下：αNE=αSE=0.2，αWE=0.8，γi=0.5。假设进入主路路段1的流量为1500 veh/h，进入辅路路段1的流量由初始路段的各相位绿信比和饱和流率计算得出。主辅路交通流模型的相关初始值如表1所示。

仿真路段在第2和第9段各有一个入口匝道，第7段有一个出口匝道。假设交叉口东西方向的饱和流率均为1 900 veh/h，南北方向上路段1和路段8的交叉口饱和流率为1 900 veh/h，其他路段的交叉口在南北方向上的饱和流率均为1 200 veh/h。假设辅路交叉口南北侧的交通需求量相同，为体现高峰时段的道路交通状况，进出口匝道和各个交叉口南北方向上的交通需求量如图2所示。

表1 交通流模型相关初始值

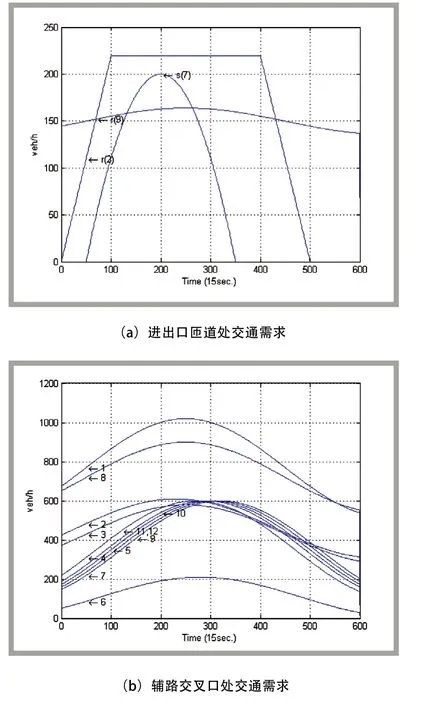
图2 主辅路系统交通需求量

3.1 入口匝道无控制,辅路交叉口采用定时控制

交叉口定时控制器设置第1相位和第2相位的绿信比均为0.5，此处仿真忽略损失时间。此种情况下的仿真结果见图3。从图3（a）中的仿真结果可以看出，主路上第9段之后的密度越来越大,已经超过了临界密度（36.75 veh/lane/km），并有向上游路段传播的迹象。从图3（b）可以看出，随着高峰时段的到来，辅路密度越来越大，最大可达到80 veh/ lane/km以上。显然主辅路均发生了严重拥堵现象，并且从图中可以看出主路路段之间、辅路路段之间和主路路段与辅路路段之间都出现了不同程度的密度差异，密度差异较大时，局部路段的拥挤状况会对相邻路段交通造成影响，拥挤状况会向相邻路段传播，并且这种情况下道路资源浪费现象也比较严重，降低了道路资源的利用率。

3.2 基于MFAC的快速路主辅路的均衡控制

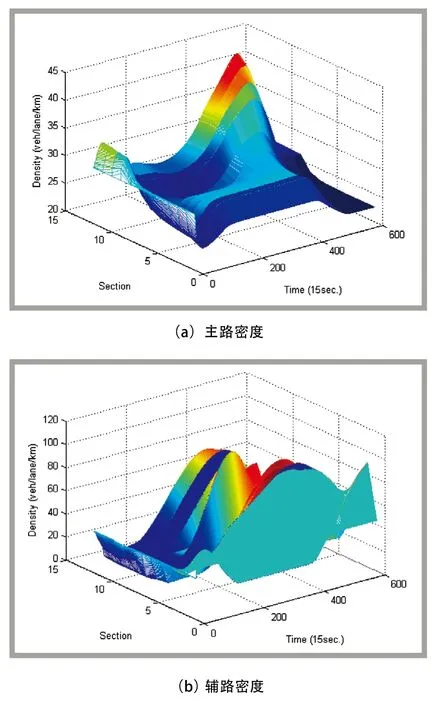
图3 情况1

该方法中MFAC控制器的参数设置如下，σ=0.8，μ=0.4，η=0.005，θ=0.001，令z1=0.008，z2= 0.002，伪偏导数矩阵初始值设置如下，

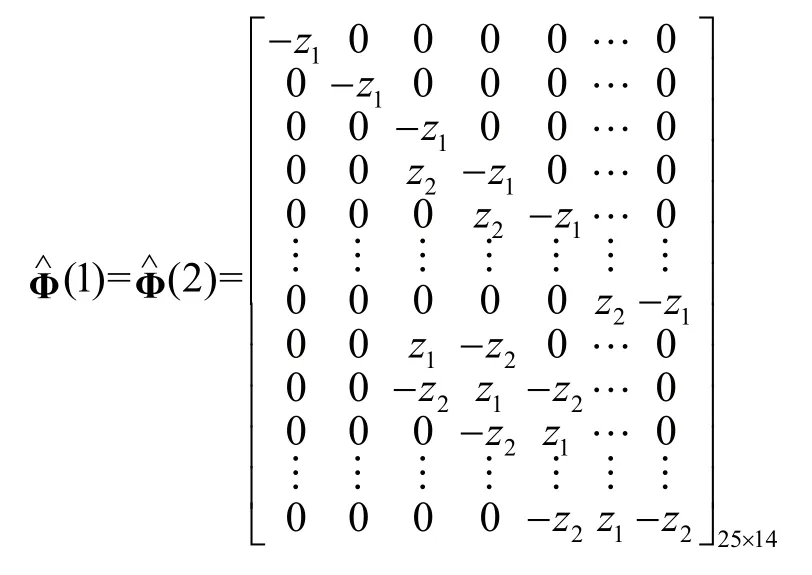
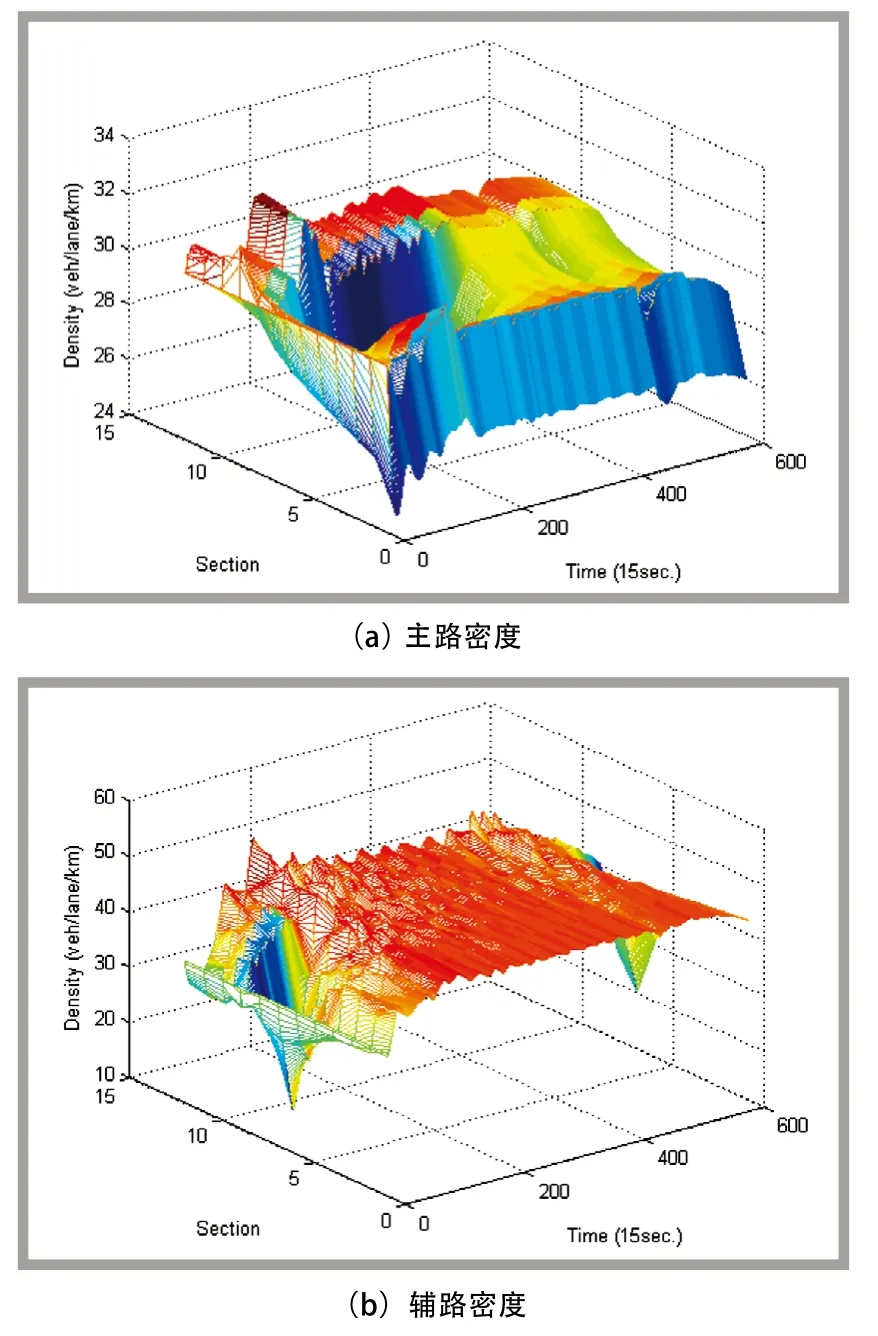
图4 情况2

4 结束语

针对快速路主辅路系统交通分布不均衡的现象，本文提出基于MFAC的快速路主辅路均衡控制方法，该方法能适应非线性快速路主辅路系统的结构和参数的时变性，通过一个控制器同时控制多个入口匝道和多个辅路交叉口，动态均衡的分配主辅路上的交通流，使主辅路达到系统的密度均衡。另外，此方法还有一些可改进的地方：考虑实际道路中的一 些情况，如两相位交叉口扩展到四相位，匝道处的排队情况等，用VISSIM等专业的交通仿真软件进行进一步的仿真验证。

[1]Parageorgiou M, Kotsialos A. Freeway ramp metering: an overview [J]. IEEE Transactions on Intelligent Transportation System, 2002, 3(4): 271-281.

[2]Varaiya P. Reducing highway congestion:an empirical approach[J]. European Journal of Control, 2005, 11(4-5): 301-309.

[3]Papageorgiou M, Hadj-Salem H, Middleham F.ALINEA local ramp metering: summary of the field results[J]. Transportation Research Record, 1997(1603): 90-98.

[4]侯忠生，晏静文. 带有迭代学习前馈的快速路无模型自适应入口匝道控制[J].自动化学报，2009，35（5）：588-595.

[5]侯忠生.非线性系统参数辨识、自适应控制及无模型学习自适应控制[D].沈阳：东北大学， 1994.

[6]侯忠生，金尚泰. 无模型自适应控制理论与应用[M]. 北京：科学出版社，2013.

[7]朱弘戈，刘小明，史其信. 基于均衡思想的快速路入口控制模型及其应用[J].交通运输系统工程与信息，2010，10（5）：85-90.

[8]Papageorgiou M, Blosseville J M, Hadj-Salem H. Macroscopic modeling of traffic flow on the Boulevard Peripherique in Paris[J]. Transportation Research Part B, 1989, 23(1): 29-47.

[9]Papageorgiou M, Diakaki C, Dinopoulou V, Kotsialos A, Wang Y. Review of road traffic control strategies[J]. Proceedings of the IEEE, 2003(91): 2043-206.

[10]Aboudolas K, Parageorgiou M, Kosmatopaulos E. Storeand-forward based methods for the signal control problem in large-scale congested urban road networks[J]. Transportation Research Part C, 2009, 17(2): 163-174.

[11]赵 艺, 陆 超, 韩英铎. 多输入多输出无模型自适应广域阻尼控制器设计[J], 清华大学学报：自然科学版, 2013, 53（4）：453-458, 464.

[12]Chi Rong-Hu, Hou Zhong-Sheng. A model-free periodic adaptive control for freeway traffic density via ramp metering[J]. Acta Automation Sinica, 2010, 36(7): 1029-1032.

[13]Lv F L, Chen H B, Fan C J, Chen S B. A novel control algorithm for weld pool control[J]. Industrial Robot, 2010 37(1): 89-96.

[14]Lu Xiao-ping, Li Wei, Lin Yong-gang. Load control of wind turbine based on model-free adaptive controller[J]. Transactions of theChinese Society for Agricultural Machinery, 2011, 42(2): 109-114, 129.

责任编辑 徐侃春

MFAC based balance control for freeway and auxiliary road

CHENG Zhihui, JIN Shangtai
( Advanced Control Systems Lab, Beijing Jiaotong University, Beijing 100044, China )

In order to solve the question of traff i c congestion and traff i c resources wasting caused by the density difference between freeway and auxiliary road, the method of balance control for freeway and auxiliary road based on MFAC was proposed. This method introduced the difference balanced control theory and was not restricted by the entrance ramp and auxiliary road intersection model. Only depending on the ramp and intersection traff i c fl ow rates as input data and the density of freeway and auxiliary road sections as output data, this method could achieve the modelfree adaptive control on strong nonlinear freeway and auxiliary road system, reach to density equilibrium on freeway and auxiliary road system. The simulation results on the Matlab platform showed the effectiveness of the method.

model free adaptive control; balance control; entrance ramp; intersection

U412.36∶TP39

A

1005-8451（2015）07-0012-05

2014-12-01

程志辉，在读硕士研究生；金尚泰，讲师。