不确定规划中可达关系的快速求解算法

龙 凤,文中华,唐 杰,王进宗

(湘潭大学信息工程学院,湖南湘潭411105)

不确定规划中可达关系的快速求解算法

龙 凤,文中华,唐 杰,王进宗

(湘潭大学信息工程学院,湖南湘潭411105)

在不确定规划领域中,通常需要在同一个不确定状态转移系统中解决多个规划问题,如果能得到不确定规划中状态之间的可达关系即可方便求解该规划问题,然而现有矩阵乘法求解可达关系时存在算法复杂度高的问题。为此,设计一种快速求解不确定规划中状态之间可达关系的算法,将确定动作和不确定动作区分处理,先求解所有确定动作的可达关系,再采用链表和队列求解不确定动作的可达关系。实验结果表明,与矩阵乘法相比,该算法能得到更全面的可达关系,且求解效率更高。

不确定规划;可达关系;智能规划;模型检测;不确定性;不确定状态转移系统

1 概述

在现实世界中,存在许多不确定性问题。相对于确定规划而言,不确定规划[1-2]能够更好地解决这些问题。这是近年来智能规划的一个热点研究领域。模型检测是智能规划中处理不确定规划问题的一个重要算法。基于模型检测[3-4]的不确定规划也成为研究热点,并取得了一些重要的成果,如:求解强、弱及强循环规划解[5-6]的提出;对不确定状态转移系统进行分层[7],删除部分无用状态序偶对,减小问题规模;不确定规划中状态之间的可达关系研究[8-9];基于模型检测的不确定规划中的状态可达性研究[10];循环或非循环可达关系[11-12]的求解;正向搜索规划解[13];观察信息约简[14-15]等。

在一个不确定状态转移系统中,求解规划问题时需要反复搜索动作来寻找目标状态。由于该搜索过程是没有方向的,如果能够得到不确定规划中状态之间的可达关系,则可以更加快速地求解规划问题,减少冗余计算,建立系统引导信息。在文献[8]中,给出了求解不确定规划中的状态之间的可达关系的算法,该算法将不确定状态转移系统转换为邻接矩阵,通过邻接矩阵的加和乘运算获得系统的可达矩阵,利用可达矩阵得到可达关系。但是,该算法在求解过程中具有一定的局限性,不能保证高效地得到可达关系。所以,本文提出一种快速求解不确定规划中状态间可达关系的算法,该算法对不确定状态系统中的一些特殊的不确定动作进行了处理,从而使得该算法可以更加高效、全面地得到不确定状态系统的可达关系。

2 相关定义

定义1一个规划领域是一个不确定的状态转移系统Σ=(S,A,γ),其中:

(1)S是一个有限状态集;

(2)A是一个有限动作集;

(3)γ:S(A→2S是状态转移函数。

其中,利用γ刻画不确定性:在s下执行动作a可能得到的结果状态集合就是γ(s,a)。若γ(s,a)非空,则称动作a在状态s下是可执行的。在状态s下可执行动作的集合记为A(s)={a:∃s∈γ(s,a)},并称(s,a)为状态动作序偶。

定义2一个规划问题是由3个变量组成的三元组P=(Σ,I,G),其中:

(1)Σ=(S,A,γ)是不确定状态转移系统;

(2)I⊆S是初始状态集合;

(3)G⊆S是目标状态集合。

定义3在一个不确定状态转移系统中,从状态si开始,执行 γ(si+1,ai+1),γ(si+2,ai+2),…,γ(sn,an)后,可能存在一条路径到达状态sx,那么,称si到sx为不确定可达。对于任意sx都必有sx∈γ(sj,aj) (1＜x＜n,0＜j＜i)。

定义4在一个不确定状态转移系统中,从状态si开始,执行 γ(si+1,ai+1),γ(si+2,ai+2),…,γ(sn,an)后,不存在任何路径能够到达状态sx,那么,称si到sx为确定不可达。其中,对于任意sx都有sx∈γ(sj,aj)(1＜x＜n,0＜j＜i)。

定义5在一个不确定状态转移系统中,从状态si开始,执行 γ(si+1,ai+1),γ(si+2,ai+2),…,γ(sn,an)后,任意一条路径都能到达状态sx,那么,称si到sx为确定可达。其中,对于任意sx都有sx∈γ(sj,aj)(1＜x＜n,0＜j＜i)。

定义6在不确定状态转移系统中,2个状态之间的可达关系用函数G(si,sj)来表示,函数G(si,sj)定义如下:

(1)G(si,sj)=0:si到sj为确定不可达;

(2)G(si,sj)=1:si到sj为确定可达;

(3)G(si,sj)=2:si到sj为不确定可达。

3 可达关系的求解算法

3.1 算法原理

文献[8]利用矩阵乘的算法来求解可达关系。该算法先将不确定状态转移系统转换为邻接矩阵,然后通过邻接矩阵的加和乘运算获得可达矩阵,时间复杂度比较高。

本文提出的可达关系求解算法是将不确定状态转移系统中确定动作和不确定动作进行区别处理。这样可以避免一些重复计算,从而提高求解效率。算法主要分为两部分:(1)处理确定动作,确定动作的起始状态到终止状态是确定可达的,只需进行简单处理。(2)处理不确定动作,首先处理确定可达的情况,若状态s是不确定动作a的起始状态,且不确定动作a的所有终止状态都能确定可达状态s′,则状态s是确定可达状态s′,然后处理不确定到达的情况,显然,去除某些不确定动作的起始状态到部分终止状态确定可达以外,余下的不确定动作的起始状态到终止状态集都是不确定可达。同时,算法保证了确定可达具有传递性,即状态a确定到达状态b,b确定可达状态c,那么状态a必定确定可达状态c。

3.2 算法分析

本文算法主要分为两部分:(1)处理确定动作,求解确定动作的可达关系;(2)处理不确定动作,采用链表和队列求解不确定动作的可达关系。设Σ=(S,A,γ)是一个不确定的状态转移系统,其中有n个状态。

处理确定动作的算法中动作起始状态为u,终止状态个数为num,终止状态为v。数组graph[i][j]表示状态i和状态j的可达关系,即graph[i][j]为0代表不可达,graph[i][j]为1代表确定可达,graph[i][j]为2代表不确定可达。

处理确定动作的算法具体如下:

状态到状态本身是确定可达的,所以,第2行、第3行表示状态到自己本身是确定可达的;第5行～第7行表示确定动作的起始状态到终止状态是确定可达;第8行中mulm代表第几个不确定动作,即不确定动作的ID号;第 10行的函数solveReach求任意2个点是否确定可达,即执行这个函数后,可以保证graph具有传递性。

函数solveReach处理的具体流程如下:

函数solveReach的代码中数组graph[i][j]表示状态i和状态j的可达关系,即graph[i][j]为0代表不可达,graph[i][j]为1代表确定可达,graph[i][j]为2代表不确定可达。第4行～第8行是确保确定可达具有传递性,即graph[i][k]= =1且graph[k][j]==1,那么就有graph[i][j]==1。

处理不确定动作时,分为确定可达和不确定可达两部分进行处理。其中,mulAcation[i][0]代表第i个不确定动作的初始状态数目(为1)和终止状态数目之和,这里假设为num+1,mulAcation[i][1]代表第i个不确定动作的初始状态的编号,mulAcation[i][2,3,…,num+1]代表第i个不确定动作的所有终止状态的编号。队列actionQue用来保存所有不确定动作的ID号。

处理不确定动作中确定可达的算法具体如下:

在处理确定可达的算法时,为了保证处理时可以进行逆向查找,将不确定动作的ID号mulm保存在saHead[v]链表中,这样可以通过这个链表找到mulm。第2行～第10行是求状态u是否能够确定到达状态i,判断算法如下:由于状态u是不确定动作act的起始状态,因此如果这个不确定动作act的所有终止状态都确定可达状态i,那说明状态u也是确定可达状态i;第12行的for循环更新每一个状态;第19行的for循环是处理的一种不确定动作嵌套的特殊情况,即不确定动作act的所有终止状态中的任意一个状态是另外一个不确定动作的起始状态,如果这个不确定动作的ID号ra还没有加入队列,则将它加入到队列中。至此,处理确定可达部分的算法结束。

处理不确定动作中不确定可达的算法具体如下:

在处理不确定可达的算法中,第2行的for循环是将所有保存在mulAction中的可达关系全部放入graph数组中,如果graph[u][v]已经为1,则不需要更新,否则将graph[u][v]置为2。至此处理不确定动作的过程结束。

在执行完处理确定动作和不确定动作的算法后,再执行一遍solveReach函数,就可以得到所有状态对之间的可达关系。

对算法时间复杂度进行分析,设规划领域中有n个状态,该算法的时间主要用于2个部分,即处理确定动作的算法和处理不确定动作的算法。这两部分中都用到了solveReach函数,对solveReach函数的时间复杂度进行分析:这部分算法的时间主要用于3个循环,而且这3个循环都要遍历规划领域中的所有状态,时间复杂度为O(n3)。对于处理确定动作的算法进行分析可知,这部分算法需要遍历规划领域的所有状态,最后需执行solveReach函数来确保确定可达的传递性,时间复杂度为O(n+n3);在处理不确定动作的算法中,假设进入队列的次数为q,且需要遍历规划领域中所有的状态,最后还需执行一遍solveReach函数,时间复杂度为O(qn+n3)。根据对这两部分算法的时间复杂度分析可知,快速求解可达关系的算法时间复杂度为O(qn+n3)。

4 算法实例分析

设Σ=(S,A,γ)是一个不确定状态转移系统,如图1所示。

图1 不确定状态转移系统

根据本文算法可知,状态到状态本身是确定可达的,即graph[i][i]=1。算法分两部分求可达关系:(1)处理确定动作,根据算法中对确定动作的处理可得graph[s1][s2]=1,即状态s1确定可达状态s2。同理,graph[s4][s7]=1,graph[s5][s7]=1,graph[s6][s7]=1,graph[s3][s6]=1,graph[s3][s1]=1。由于算法保证确定可达具有传递性,且有graph[s6][s7]=1,graph[s3][s6]=1,因此有graph[s3][s7]=1。(2)处理不确定动作,如图 1所示,该不确定状态转移系统有 3个不确定动作T1,T2,T3。对于T1有graph[s4][s7]=1,graph[s5][s7]=1,即不确定动作T1的终止状态集确定可达状态s7。所以根据算法可得,该不确定动作的起始状态s2也确定可达状态s7,即graph[s2][s7]=1,因此更新状态s2和状态s7之间的可达关系。同时,由于graph[s1][s2]=1,根据传递性有graph[s1][s7]=1,因此更新状态s1和状态s7之间的可达关系。同理,对于T2,T3可以得到graph[s3][s7]=1,更新这个可达关系。

至此已完成确定可达情况的处理,接下来处理不确定可达的情况。根据处理不确定动作的算法可知,对于T2有graph[s3][s1]=2,由于上文已得到状态s3和状态s1之间为确定可达,因此不需要更新这个可达关系,仍为graph[s3][s1]=1;graph[s3][s5]=2,更新这个可达关系。同理,对于T1,T3可以得到graph[s2][s4]=2,graph[s2][s5]=2,graph[s3][s5]=2,更新这些可达关系。

在执行solveReach函数后得到graph[s1][s4]=2,graph[s1][s5]=2,graph[s3][s4]=2。

所以,该不确定状态转移系统的确定可达关系和不确定可达关系如下:

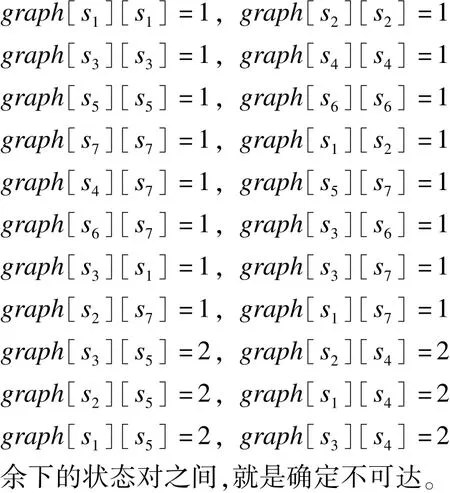
5 实验结果及分析

实验环境均为Windows7+Core(TM)i3-3220

3.3 GHz+4.0 GB内存 +VC6。实验数据随机生成。

表1为文献[8]中求状态可达关系的算法与本文提出快速求解状态可达关系算法的实验结果比较。

表1 执行时间对比 s

由表1可知,当不确定状态转移系统中的状态数目较少时,文献[8]中的矩阵乘算法和本文算法的运行时间都很短,此时本文算法的优势不明显。当不确定状态系统中的状态数目较多时,本文算法的优势便突显出来,证明它在求解可达关系时具有更高的效率。随着状态数的增长,由于时间复杂度不同,矩阵乘的运行时间增长速度较快,而本文算法的运行时间则增长平缓。

从实验结果及分析可以看出,采用本文算法可以更加快速地得到不确定系统状态之间的可达关系。

6 结束语

本文提出一种快速求解状态可达关系的算法。通过实例说明,本文算法可以更加高效、全面地得到不确定状态系统的可达关系。在求解状态可达关系的基础上,下一步将对以下工作进行研究:(1)基于可达关系求多Agent规划解;(2)对状态转移系统中的动作增加权值,求确定可达的状态最短路径。

[1] Huang Wei,Wen Zhonghua,Jiang Yunfei,etal. Comparison Between Two Languages Used to Express Planning Goals:CTL and EAGLE[C]//Proceedings of PRICAI’06.[S.l.]:Springer-Verlag,2006:180-189.

[2] Roveri C M.Conformant Planning via Model Checking and Heuristic Search[J].Artificial Intelligence,2004, 159(1/2):127-206.

[3] Bertoli P,Cimatti A,Roveri M,et al.Strong Planning Under Partial Observability[J].Artificial Intelligence, 2006,170(1):337-384.

[4] Roveri C M,Traverso P.Automatic OBDD-based Generation ofUniversalPlansin Non-deterministic Domains[C]//Proceedings of AAAI’98.Madison, USA:AAAI Press,1998:26-30.

[5] Cimatti A,Pistore M,Rovveri M,et al.Weak,Strong,and Strong Cyclic Planning via Symbolic Model Checking[J]. Artificial Intelligence,2003,147(1/2):35-64.

[6] 陈建林.强规划解、弱规划解的研究[D].湘潭:湘潭大学,2011.

[7] 文中华,黄 巍,刘任任,等.模型检测规划中的状态分层算法[J].软件学报,2009,20(4):858-869.

[8] 文中华,黄 巍,刘任任,等.模型检测规划中的状态之间的可达关系研究[J].计算机学报,2012,35(8): 1634-1643.

[9] 黄丽芳.基于不确定系统的状态可达关系求规划解的算法研究[D].湘潭:湘潭大学,2013.

[10] 胡雨隆.基于模型检测的不确定规划中的状态可达性研究[D].湘潭:湘潭大学,2012.

[11] 黄丽芳,文中华,胡雨隆,等.不确定规划中状态循环可达关系的求解算法[J].计算机应用研究,2013, 30(9):2689-2693.

[12] 胡雨隆,文中华,常 青,等.不确定规划中状态非循环可达关系的求解算法[J].计算机仿真,2012, 29(5):114-117.

[13] 陈建林,文中华,朱 江,等.正向搜索算法求强规划解[J].计算机工程与应用,2011,47(6):52-54.

[14] Huang Wei,Wen Zhonghua,Jiang Yunfei,etal. Structured Plans and Observation Reduction for Plans with Contexts[C]//Proceedings of IJCAI’09. Pasadena,USA:AAAI Press,2009:1721-1728.

[15] Huang Wei,Wen Zhonghua,Jiang Yunfei,et al.Observation Reduction for Strong Plans[C]//Proceedings of IJCAI’07.Hyderabad,India:AAAI Press,2007:1930-1935.

编辑 陆燕菲

Fast Solving Algorithm of Reachability Relation in Uncertain Planning

LONG Feng,WEN Zhonghua,TANG Jie,WANG Jinzong
(College of Information Engineering,Xiangtan University,Xiangtan 411105,China)

In uncertain planning field,it is frequent to solve many planning problems over a nondeterministic statetransition system in uncertain planning.So getting the state reachability for the nondeterministic state-transition system can make solving planning problems easier.However,the existing solution matrix multiplication of relations exist the problem of high algorithm complexity.Therefore,this paper presents a fast solving algorithm of reachability relation between the states in uncertain planning.The algorithm determines the certainly action and uncertainty actions separately.It determines the relationships between the certainty action,then solves relations between uncertain actions with lists and queues. Experimental result shows that the algorithm not only can get a more comprehensive relationship,but also has higher efficiency than the matrix multiplication algorithm.

uncertain planning;reachability relation;intelligent planning;model checking;uncertainty;uncertain statetransition system

1000-3428(2015)01-0196-04

A

TP18

10.3969/j.issn.1000-3428.2015.01.036

国家自然科学基金资助项目(61070232,61272295)。

龙 凤(1989-),女,硕士研究生,主研方向:智能规划;文中华,教授、博士生导师;唐 杰、王进宗,硕士研究生。

2013-12-30

2014-03-26 E-mail:416807936@qq.com

中文引用格式:龙 凤,文中华,唐 杰,等.不确定规划中可达关系的快速求解算法[J].计算机工程,2015,41(1): 196-199.

英文引用格式:Long Feng,Wen Zhonghua,Tang Jie,et al.Fast Solving Algorithm of Reachability Relation in Uncertain Planning[J].Computer Engineering,2015,41(1):196-199.