不确定规划中的多Agent带权值强规化算法

伍小辉,文中华,李 洋,劳佳琪

(湘潭大学信息工程学院,湖南湘潭411105)

不确定规划中的多Agent带权值强规化算法

伍小辉,文中华,李 洋,劳佳琪

(湘潭大学信息工程学院,湖南湘潭411105)

在智能规划领域中,以往对不确定规划问题的研究主要集中于单个Agent,而对多Agent规划的研究则侧重于确定规划。针对该问题,提出基于多Agent的带权值不确定规划问题,对所求解的强规划解,设计使其所需动作权值总和近似最小的算法。根据基于模型检测的强规划分层方法,对每个Agent进行强规划分层,合并所有Agent的分层信息,并在合并的过程中得到同层状态之间的冲突表。在保证冲突最小的情况下,以最小动作权值优先的贪心方法,求出强规划解。实验结果表明,该算法能较快地求解出使所选择的动作权值总和近似最小的强规划解。

多Agent规划;不确定规划;强规划解;模型检测;动作权值;智能规划

1 概述

智能规划[1]是人工智能研究领域的一个重要分支,多Agent规划[2]包含多个Agent的规划问题[3-4]。不确定规划[5-6]和多Agent规划在近年的IJCAI和AAAI中都有专门的会议。

以往对于不确定规划的研究主要侧重于单个Agent,而对于多Agent规划的研究又着重于确定规划。因为实际的规划问题存在很多不确定因素,所以今后的多Agent规划研究必然会考虑不确定动作;而单个Agent的不确定规划其实是基于多Agent的不确定规划问题的一个特例(即Agent数目为1)。众所周知,多Agent规划和不确定规划都是当今非常热的研究领域,具有很重要的理论和应用价值,所以在基于多Agent的不确定规划问题上的研究工作是非常有意义的。

文献[7]最先提出了强规划解的概念。文献[8]又给出了有关弱规划解、强规划解和强循环规划解的完整定义和说明。一直以来,求强规划解都是不确定规划研究中的热点,因为相对于弱规划解和强循环规划解[9]而言,强规划解更具有理论和应用价值。另外,以往对于规划的研究主要侧重于规划解本身,但是考虑到现实世界中,每个动作的执行都是有耗费的,文献[10]在不确定规划中考虑了动作耗费的问题,并将其称作动作权值。

本文将多Agent规划和不确定规划的研究相结合,引入动作权值的概念,在不确定规划中提出基于多Agent的带权值问题,并设计了求解强规划解的算法,且该算法使所求得的强规划解所需的动作权值总和近似最小。

2 相关定义

定义1(不确定规划领域) 不确定规划领域Σ=＜S,A,γ＞。其中,S是一个有限状态集;A是一个有限动作集;γ.S×A→2S是状态转换函数。

γ用来表示不确定性,γ=(s,a)表示状态s执行动作a所得到的状态集合;若γ=(s,a)非空,则称动作a在状态s下是可执行的。在状态s下可执行的动作集合记作A(s)={a:∃s′∈γ(s,a)};其中,称s′是s可达的,称(s,a)为状态动作序偶;且至多存在一个动作a,使得s′是s可达的。

定义2(不确定规划问题) 不确定规划问题P=＜Σ,I,G＞。其中,Σ是不确定规划领域;I⊆S是初始状态集合;G⊆S是目标状态集合。

定义3(不确定规划的执行结构) 不确定规划的执行结构K=＜Q,T＞。其中,Q⊆S和T⊆S×S是满足以下条件的最小集合:

(1)若s∈S,那么s∈Q,并且满足(2);

(2)若s∈Q且存在某个动作a使得(s,a)∈π,那么对所有的s′(其中s′∈γ(s,a)),都有s′∈Q且(s,s′)∈T。

状态s∈Q是K的一个终止状态当且仅当不存在状态s′∈Q,使得(s,s′)∈T。K是一个有向图,其中,Q是在执行规划解时能够到达的所有状态集合;T表示所有可能的状态转移。显然,K的终止状态代表规划执行的终止,这里用Sterminal(K)表示执行结构K的终止状态集。

定义4(不确定规划的规划解) 设Σ=＜S,A, γ＞是一个不确定规划领域,P=＜Σ,I,G＞是Σ上的一个不确定规划问题,π是不确定规划领域Σ中的一个状态动作序偶表,K=＜Q,T＞是π从S导出的执行结构。

(1)π是P的弱规划解当且仅当(∀s∈I) (∃s′∈G∩Sterminal(K)),其中s′是s可达的。

(2)π 是P的强循环规划解当且仅当Sterminal(K)⊆G,且(∀s∈Q)(∃s′∈Sterminal(K)),其中s′是s可达的。

(3)π是P的强规划解当且仅当K是无环的,且Sterminal(K)⊆G。

若P有强规划解,则称可以从初始状态强到达目标状态。

定义5(基于多Agent的带权值不确定规划领域) 基于多Agent的带权值不确定规划领域D=＜n,Σi=1,2,…,n,m,Wj=1,2,…,m＞。 其中,n表示 Agent的数目;Σi表示Agenti的不确定规划领域;m表示动作的数目;Wj表示执行动作aj需要耗费的权值。

定义6(基于多Agent的带权值不确定规划问题) 基于多Agent的带权值不确定规划问题Ψ=＜D,n,Pi=1,2,…,n,S0,Sg＞。 其中,D表示基于多Agent的带权值不确定规划领域;n表示Agent的数目;Pi表示Agenti的不确定规划问题;S0⊆S是基于多Agent的带权值不确定规划问题的初始状态集合;Sg⊆S是基于多Agent的带权值不确定规划问题的目标状态集合。

定义7(基于多Agent的带权值不确定规划问题的强规划解) 设D=＜n,Σi=1,2,…,n,m,Wj=1,2,…,m＞是一个基于多Agent的带权值不确定规划领域,Ψ=＜D,n,Pi=1,2,…,n,S0,Sg＞是D上的一个基于多Agent的带权值不确定规划问题;那么在Ψ上的强规划解 Π =(n,πi=1,2,…,n,wi=1,2,…,n),其中,n表示Agent的数目;πi表示Agenti在Pi上的强规划解;wi表示Agenti在Pi上的近似最小动作耗费值。基于多Agent的带权值不确定规划问题的强规划解Π保证任意一个Agent在执行对应的动作序列的过程中不会出现冲突情况,并且能使每个Agent都能强到达自己的目标状态(所有Agent是在同一时间执行动作,没有先后顺序)。

图1是一个基于多Agent的带权值不确定规划领域D,其中,动作ai后面括号中的数值是执行该动作需要耗费的权值,如a1(2)表示执行动作a1需要耗费的权值为2。

图1 基于多Agent的带权值不确定规划

假设在D上有一个基于多Agent的带权值不确定规划问题Ψ=＜D,2,P1,2,S0,Sg＞。其中,P1=＜Σ1,I1,G1＞;P2=＜Σ2,I2,G2＞,且 Σ1=Σ2;I1={s1,s2};G1={s7,s8};I2={s2};G2={s8};S0={s1,s2};Sg={s7,s8}。

那么求得的解为 Π =(2,π1,2,w1,2)。其中, π1={(s1,a1),(s3,a7),(s4,a8)};w1=7;π2={(s2,a3),(s6,a6),(s5,a9)},w2=13。

3 SPSMNPW算法

本文提出求解基于多Agent的带权值不确定规划问题的强规划解的算法(Strong Planning Solution for Multi-agent Nondeterministic Planning with Weight,SPSMNPW)。

3.1 算法思想

算法首先使用基于模型检测的强规划分层方法[11-12],对每个Agent进行分层。由定义7可知,基于多Agent的带权值不确定规划问题的强规划解保证了每个Agent都有强规划解;于是在单个Agent强规划分层的时候,如果某个Agent分层失败,即可判断该规划问题没有规划解。它可以迅速排除那些因单个Agent无强规划解而导致整个规划问题没有强规划解的规划问题,从而减少了搜索时间;在Agent个数和状态数很大时,优化效果非常明显。

在得到每个Agent的强规划分层后,根据整个规划问题的初始状态集合动态的合并分层,并在合并分层的过程中求得每一层每个状态的冲突表。可以使用搜索算法得到所有的强规划解,然后从中选出动作权值总和最小的解;但是求解的时间复杂度太高。所以本文利用冲突表,在保证动作所到达状态的冲突最小的情况下,以最小动作权值优先的贪心算法,可以快速求解出强规划解,且所求得的强规划解的动作权值总和近似最小。如果求解的过程中遇到冲突,则使用后文的Solve-Conflicting()函数来处理冲突。

3.2 算法实现

SPSMNPW算法的主要流程如下:

第2行～第6行是根据模型检测中的强规划分层方法对每个Agent进行分层;如果某个Agent分层失败,说明该Agent没有强规划解,而基于多Agent的带权值不确定规划问题的强规划解要求每个Agent都要有强规划解,所以可以直接判断这个规划问题没有强规划解,于是返回noSPSolution。

第7行是执行多Agent强规划函数,并返回强规划解的状态动作序偶表和得到该规划解所需的动作权值总和。

单个Agent的分层算法流程如下:

第3行是将AgentInfo[i]的目标状态集合作为第1层。

第4行～第9行是对AgentInfo[i]进行分层。如果上一次分层为空,则跳出while()循环,返回false。否则,继续执行while()循环结构中的程序;若初始状态集合中还有元素尚未包含于singleH[i]分层中时,则使用函数Sel_NL()来选择下一层的状态加入singleH[i][++layer]中;若初始状态集合中的元素全部包含于singleH[i]分层中,则返回true。

强规划算法流程如下:

第2行的函数是根据多Agent不确定规划的初始状态集合S0和目标状态集合Sg,将所有Agent的单个分层singleH进行合并。首先把S0中的元素作为wholeH的第1层;然后搜索wholeH第1层中的元素在singleH中可达的状态,加入wholeH的第2层;如此类推,搜索wholeH第i层中的元素在singleH中可达的状态,加入wholeH的第i+1层,直到所有状态到达目标状态集合Sg。这种动态合并的算法可以去除不必要的状态,且在合并的过程中可以求得wholeH中每一层每个状态的冲突表confSet。

第3行～第6行是从AgentInfo[1]的第1层开始,当sA有效时,在while()循环中执行SPS-Search()函数,搜索满足条件的强规划解。

第7行～第10行判断是否所有的Agent都找到了强规划解。如果存在Agent没有找到强规划解,则返回false;否则,返回强规划解的状态序偶表π和得到该强规划解所需的动作权值之和w。

强规划解搜索算法流程如下:

第3行是当搜索的层数小于1时,搜索无效,返回。

第4行～第6行是当AgentInfo[i]到达目标状态时,则调用Get_Next_Agent(sA)函数。Get_Next_Agent(sA)函数返回下一次搜索的Agent和搜索的层数;当i等于n时,下一次搜索的Agent为1,搜索的层数为j+1;当i不等于n时,下一次搜索的Agent为i+1,搜索层数不变。

第7行 ～第29行是判断AgentInfo[i][j]的sourceStatus集合中的每个状态是否都能到达下一层。第9行的Priority_Action_Seq()函数是利用冲突表confSet,在冲突最小的情况下,以最小代价优先的贪心算法搜索得到状态s的动作集合actionSet。第10行～第21行是判断actionSet中是否存在动作a能强到达下一层;若存在,则更新相关的值,并置noConflictFlag为true,跳出循环。如果不存在,则执行第22行～第28行。其中,在第23行中判断此次搜索是否来自Solve-Conflicting()函数的调用;若是,返回无效的sA;否则,执行第25行,调用Solve-Conflicting()函数,处理冲突。在第27行中,当判断sA.layer≠sA′.layer时,说明处理冲突失败,返回sA′;否则,继续执行for循环。

第30行 ～第31行是搜索成功,更新记录该Agent信息的数组AgentInfo,并返回下一次搜索的Agent和搜索的层数。

处理冲突算法流程如下:

第2行对AgentInfo和Flag进行备份,冲突解决不了时可以恢复数据,避免数据修改之后无法恢复。

第3行 ～第13行是处理冲突的具体实现。第3行是从actionSet中选出一个动作a。第4行是判断当AgentInfo[index]选择动作a以后,从动作a所能到达的所有状态中选择一个状态sj。第5行的GetConflictingAgent(sj)函数是找出在状态sj上造成冲突的Agent集合agentT。第6行～第8行是对集合AgentT中的任意元素Ai,判断使用SPS-Search(sA′=(Ai,layer))函数是否能够解决冲突;如果存在某个Agent无法解决冲突,则跳出循环。第10行是如果动作a在layer+1层所能到达的所有状态sj都能解决冲突,则跳出循环去执行第18行并返回sA。

第14行～第18行是当无法解决冲突时,恢复AgentInfo和Flag的值;并将layer-1,然后返回sA;也就是搜索AgentInfo[index]的上一层来解决冲突。

3.3 算法分析

3.3.1 复杂度分析

该算法的时间耗费主要包括3个方面:Agent分层,分层合并;强规划解搜索。设Agent数为n,状态集大小为sn,动作集大小为m。

通过分析上文的算法可知,Agent分层的最坏时间复杂度为O(sn2);分层合并的最坏时间复杂度为O(n×sn×m);强规划解搜索的最坏时间复杂度为O(n×sn2×m)。显然,SPSMNPW算法的时间复杂度为O(n×sn2×m)。

设x=max{sn,m},则算法的空间复杂度为O(n×sn×x)。

3.3.2 算法正确性证明

定理1基于多Agent的带权值不确定规划问题有强规划解的必要条件是每个Agent的强规划分层成功。

证明:由定义7可知,基于多Agent的带权值不确定规划问题的强规划解要求每个Agent都有强规划解;又根据文献[12]的定理1可以证明,Agent有强规划解的充分必要条件是它的强规划分层成功。

所以每个Agent的强规划分层成功是基于多Agent的带权值不确定规划问题有强规划解的必要条件。

定理2强规划算法Multi-Agent-SP()是正确的。

证明:强规划算法能够判断一个基于多Agent的带权值的不确定规划问题是否有强规划解,因为该算法的终止只有2种情况:(1)每个Agent在不冲突的情况下都能求得强规划解;(2)Agent之间因为冲突无法解决,最终逆向收敛于第1层。

而在状态转移时,每个状态只会出现下面3种情况:(1)状态通过执行相应动作可以顺利转移到下一层;(2)状态转移到下一层时会造成冲突,但是最终可以解决冲突;(3)状态转移到下一层时会造成冲突,且冲突无法解决,从而返回上一层解决冲突。

从上面的分析可知,如果状态出现第(1)种、第(2)种情况,则可以转移到下一层,且当所到达的下一层状态是终止状态时,该状态的搜索结束;如果从初始状态扩展的所有状态都最终到达终止状态,则找到强规划解,结束。

如果状态出现第(3)种情况,则返回上一层,并记录上一次搜索结果;然后重新搜索与之前所记录结果不同的搜索结果;如果存在,则转移到下一层继续搜索;否则,再返回上一层解决冲突。如此循环,最终要么冲突解决,搜索得到强规划解;要么返回到第1层,且无法解决冲突,可判断该问题无强规划解。

据上述分析可证明算法Multi-Agent-SP()是正确的。

算法SPSMNPW是由定理1和定理2的结论组成的,所以可以证明算法SPSMNPW是正确的。

4 实验结果及分析

根据本文提出的算法SPSMNPW设计实验,可以较快求出基于多Agent的不确定规划问题强规划解,且所需的动作权值之和近似最小。通过实验证明了该算法的正确性和有效性。

本文设计了一个随机算法,首先使用srand(time(0))避免伪随机;然后设定Agent和状态数;再使用rand()函数随机生成测试所需的初始状态集、目标状态集、动作集等相关数据;且为了更为客观精确地测试算法的效率,动作所关联的状态编号和状态个数也用rand()函数随机生成。通过该算法生成了1 000组在Agent个数为2,4,6,8,10,状态数为50,70,90,110, 130,150时的样例。使用SPSMNPW算法编写的程序在这1 000组样例上分别执行10次的平均时间如表1所示。

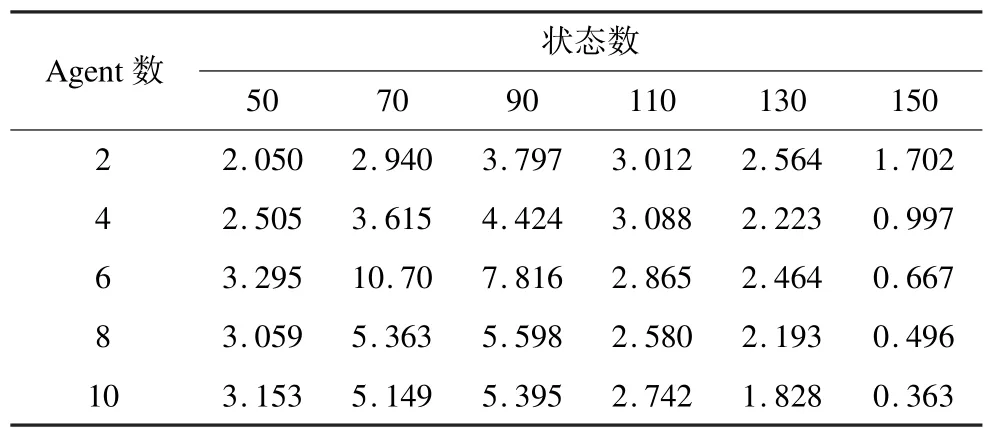
表1 1 000组样例的平均执行时间 s

通过观察实验数据,发现实验结果与预期存在差异。实验预期应该是:横向比较时,随着Agent个数的增加,冲突的概率增大,处理冲突会耗费更多的时间,所以运行时间会逐渐增长;纵向比较时,随着状态数的增加,Agent需要判断的状态数增加,分层的层数也会增加,运行时间也会逐渐增长。

通过进一步研究和分析,发现随着Agent的个数和状态数的增加,找不到规划解的概率也会增大,当超过某一数值时,这种增长会非常迅速。而在SPSMNPW算法中可以通过执行单个Agent分层算法去掉那些因单个Agent无强规划解而导致整个多Agent不确定规划领域无强规划解的样例。此外, Multi-Agent-SP算法中也优化了因为无法解决冲突而提前结束搜索的情况。

为验证上述分析的正确性,本文再次设计了实验。首先根据SPSMNPW算法,在Agent个数为2, 4,6,8,10,状态数为50,70,90,110,130,150时,分别找出100组可以找到强规划解的样例。再次使用SPSMNPW算法在这100组样例上分别执行10次,所需的平均时间如表2所示。

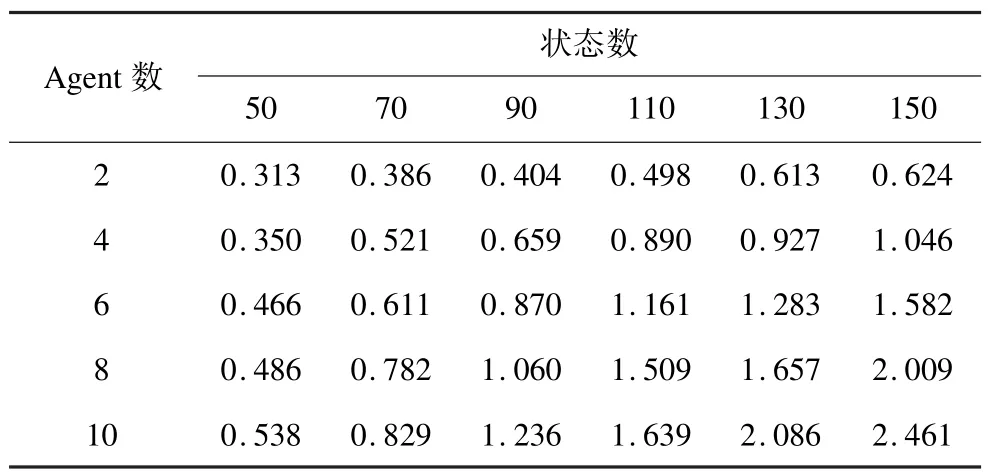
表2 1 00组样例的平均执行时间 s

通过表2,可以验证之前对于表1结果不符合预期的分析是正确的。表2的结果显示,随着Agent的个数增加,运行时间增长;随着状态数的增加,时间也增长;实验结果符合预期。

5 结束语

针对基于多Agent的带权值不确定规划问题,本文设计了一个求强规划解的算法。该算法使用了基于模型检测的强规划分层法,可以快速解决因单个Agent无强规划解而导致的在整个规划领域无强规划解的问题,从而减少搜索,达到优化的目的。此外,在搜索过程中,使用冲突表confSet进行优化,尽可能避免冲突。另外,因为使用了以最小动作权值优先的贪心算法,所以使问题可以在多项式时间内解决,且最终求得的强规划解所需的动作权值之和近似最小。实验结果验证了算法的有效性。

今后还可以从以下2个方面进行研究:(1)求解多Agent不确定规划领域的强循环规划解和弱规划解;以及最小动作权值的强循环规划解和弱规划解。(2)在全可观察和部分可观察条件下,对多Agent不确定规划领域上的观测信息进行约简。

[1] Ghallab M,Nau D,Traverso P.Automated Planning Theory and Practice[M].[S.l.]:Morgan Kaufmann Publishers,2004.

[2] Weiss G.Multiagent Systems:A Modern Approach to Distributed Artificial Intelligence[M].[S.l.]:MIT Press,1999.

[3] Yang Qiang,Wu Kangheng,Jiang Yunfei.Learning Action Models from Plan Examples Using Weighted Max-SAT[J].Artificial Intelligence,2007,171(2/3): 107-143.

[4] Gil Y.Description Logics and Planning[J].AI Magazine,2005,26(2):73-84.

[5] 饶东宁,蒋志华,姜云飞,等.对不确定规划中观察约简的进一步研究[J].软件学报,2009,20(5): 1254-1268.

[6] Cimatti A,Roveri M,Traverso P.Automatic OBDD-based Generation of Universal Plans in Nondeterministic Domains[C]//Proceedings of the 15th National Conference on Artificial Intelligence.Madison,USA:[s.n.], 1998:875-881.

[7] Cimatti A,Roveri M,Traverso P.Strong Planning in Nondeterministic Domains via Model Checking[C]// Proceedings of the 4th International Conference on Artficial Intelligence Planning Systems. Pittsburgh, USA:[s.n.],1998:36-43.

[8] Cimatti A,Pistore M,Roveri M,et al.Weak,Strong,and Strong Cyclic Planning via Symbolic Model Checking[J]. Artificial Intelligence,2003,147(1/2):35-84.

[9] Fu Jicheng,Ng V,Bastani F B,et al.Simple and Fast Strong Cyclic Planning for Fully-observable Nondeterministic Planning Problems[C]//Proceedings of the 22nd International Joint Conference on Artificial Intelligence.Barcelona,Spain:[s.n.],2011:1949-1954.

[10] 陈建林,文中华,马丽丽,等.一种求解最小权值强规划的方法[J].计算机工程,2011,37(17):167-171.

[11] Cimatti A,Roveri M.Conformant Planning via Model Checking and Heuristic Search[J].Artificial Intelligence,2004,159(1/2):127-206.

[12] 文中华,黄 巍,刘任任,等.模型检测规划中的状态分层方法[J].软件学报,2009,20(4):858-869.

编辑 顾逸斐

Multi-Agent Strong Planning Algorithm with Weight in Nondeterministic Planning

WU Xiaohui,WEN Zhonghua,LI Yang,LAO Jiaqi
(College of Information Engineering,Xiangtan University,Xiangtan 411105,China)

In the field of intelligent planning study,previous studies of nondeterministic planning focus on a single Agent,and research on multi-Agent planning focuses on determining planning.To solve this problem,this paper presents the cost strong planning problem in multi-Agent nondeterministic planning domain,and designs the strong planning algorithm to solve strong planning solution with approximate minimum sum of action cost.Based on model checking of strong hierarchical planning methods to make strong hierarchical planning for each Agent,it merges all Agent’s hierarchical information,and gets the conflicting table of the same level between states in the process of merging at the same time.Under guaranteeing minimum conflicting,this paper uses greedy method for minimum action cost priority to solve a strong planning solution.Experimental results show that the algorithm not only can solve strong planning solution with approximate minimum sum of action cost,but also runs quickly.

multi-Agent planning;nondeterministic planning;strong planning solution;model checking;action weight; intelligent planning

1000-3428(2015)01-0190-06

A

TP301.6

10.3969/j.issn.1000-3428.2015.01.035

国家自然科学基金资助项目(61070232,61272295,61105039)。

伍小辉(1988-),男,硕士研究生,主研方向:智能规划;文中华,教授、博士生导师;李 洋、劳佳琪,硕士研究生。

2013-12-23

2014-03-06 E-mail:510280596@qq.com

中文引用格式:伍小辉,文中华,李 洋,等.不确定规划中的多Agent带权值强规化算法[J].计算机工程,2015, 41(1):190-195.

英文引用格式:Wu Xiaohui,Wen Zhonghua,Li Yang,et al.Multi-Agent Strong Planning Algorithm with Weight in Nondeterministic Planning[J].Computer Engineering,2015,41(1):190-195.