小型移动机器人自主返航路径规划方法

姜 涛,王建中,施家栋

(北京理工大学爆炸科学与技术国家重点实验室,北京100081)

小型移动机器人自主返航路径规划方法

姜 涛,王建中,施家栋

(北京理工大学爆炸科学与技术国家重点实验室,北京100081)

针对遥控小型移动机器人在自主返航实际应用中定位精度低等问题,提出一种小型移动机器人自主返航路径规划方法。介绍小型移动机器人的任务流程及硬件系统,利用膨胀算子对栅格地图中的障碍物进行运算得到栅格Voronoi图。使用双边界路径矢量化方法从栅格Voronoi图中提取出矢量路径,并对该路径进行拓扑优化。通过Dijkstra算法对拓扑路径进行路径规划并进行算法验证。实验结果表明,该方法所得路径可使环境中的机器人与障碍物之间的距离最大化,并使移动机器人的运动轨迹具有较高的可执行性,提高了小型移动机器人自主返航的成功率。

移动机器人;数学形态学;路径规划;Voronoi图;拓扑优化;Dijkstra算法

1 概述

小型移动机器人主要用于城市巷战执行侦察任务,通常采用遥控方式进入侦察区域,在楼宇间或房屋楼道内进行情报搜集。在实际使用过程中,遥控信号在楼群或室内极易被遮挡与屏蔽,所以需要移动机器人在失去控制时进行路径规划使其具有自主返航能力。

路径规划是从一个地方运动到另一个地方的路径问题。其主要目的是为移动机器人规划出最优路径,使平台安全高效的到达目的地,目前所提出的计算方法多数以寻求全局最优解为目标。A∗算法引入启发式函数引导搜索方向,提高了搜索效率。通过对估价函数和图搜索方向的改进,可以提高路径规划速度,具有一定复杂环境适应能力[1]的遗传算法是基于自然选择和基因遗传学原理的随机搜索算法,其采用多点搜索有更高概率搜索到全局最优解[2]。人工神经网络方法是对人脑的模拟,该方法具有并行处理效率高,学习能力强,能收敛到最优路径[3]。模糊算法运用近似自然语言方式,可较好处理数据不确定性和非精确性[4]。粒子群算法属于进化算法的一种,以随机解出发通过迭代寻找最优解,该方法具有易实现、高精度和快收敛等特点[5-6]。蚁群算法是一种模拟蚂蚁群体智能行为的仿生优化算法,具有较强的鲁棒性与适应性[7-8]。侦察类移动机器人体积较小,自身携带的传感器数量与重量都有严格限制,导致其智能化水平与定位导航精度较低,所以创建与规划的返航路径需要有较高的可执行性,才可以满足实际使用要求。

本文针对小型移动机器人在自主返航实际应用中所存在的问题,提出一种小型移动机器人自主返航路径规划方法。介绍侦察类小型移动机器人的任务流程,设计移动机器人的硬件系统。对所建立的栅格地图进行障碍物膨胀运算,使用双边界路径矢量化方法提取矢量路径,并对该路径进行拓扑优化。利用Dijkstra算法进行路径规划,通过实验验证该算法的可行性。

2 小型移动机器人任务流程及系统结构

在遥控侦察的过程中机器人除了执行任务外,自身所携带的多种传感器自动对周围环境进行地图创建与定位。当遥控信号被周边楼群遮挡或被室内墙壁屏蔽,或者任务执行完成,移动机器人将根据所建立的环境地图规划出一条最优路径,实现移动机器人的自主返航。

小型移动机器人系统构架主要由传感器系统、控制系统和运载系统组成。传感器系统使用激光雷达与捷联惯导组合方式,进行环境地图创建与定位。激光雷达型号为单线UTM-30LX;微机电捷联惯导型号为3DM-GX3-45,该惯导重量为23 g,适合安装在微小型移动机器人上进行导航定位。控制系统采用NI sbRIO-9626嵌入式控制板,该控制板采用Freescale的MPC5125微处理器,内嵌VxWorks操作系统。本文所设计的自主返航路径规划方法在该控制板上实现。运载系统采用NI Single-Board RIO机器人,该移动机器人机构及相应系统部件安装如图1所示。

图1 小型移动机器人平台

3 路径网创建及返航路径优化

移动机器人在探索环境时建立了与之对应的栅格地图,通过对栅格地图的处理得到了小型移动机器人自主返航路径,其方法流程如图2所示。首先,利用数学形态学中的膨胀算子对栅格地图所描述的障碍物进行膨胀运算,生成了栅格Voronoi图,形成了一组返航路径网;其次,对路径网进行双边界路径矢量化得到矢量路径网,便于移动机器人运动控制系统执行;再次,为了减少数据存储空间,提高路径规划效率,将矢量路径进行拓扑化;最终,通过Dijkstra算法对拓扑路径进行路径规划选出一条最优返航路径。

图2 路径规划方法流程

3.1 结构元素选择方法

结构元素是用于探测当前栅格地图的一个集合,在进行形态学运算时需要首先选择结构元素才可以进行形态学运算,如图3所示3种结构元素分别为正方形、钻石形和线段形,其原点在结构元素的几何中心位置。结构元素的形状和尺寸必须适合于待处理目标障碍的几何性质,方形结构元素适合处理建筑物等方形障碍物目标,线段结构元素适合处理线形目标[9]。本文所需处理的目标对象为楼道、房屋等室内环境地图,所以选择正方形作为结构元素。

图3 结构元素形状

3.2 数学形态学基本运算

腐蚀算子以数学形态学为数学基础,利用结构元素B对集合X进行腐蚀可表示为εB(X),其定义为当B的原点在x,B包含于X内的x的所有轨迹点,则:

其中,εB(X)为在移动结构元素的过程中,可以填入X内部的结构元素的所有原点组成,并具有收缩栅格地图中障碍物的作用。

膨胀为腐蚀运算的逆运算,利用结构元素B对集合X进行膨胀表示为δB(X),δB(X)是腐蚀结果的补集,可表示为:

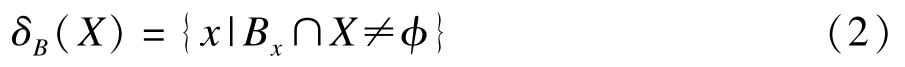
在利用结构元素对集合X进行膨胀,结果使集合X扩大,该性质具有膨胀栅格地图中障碍物的作用。

3.3 基于膨胀算子的栅格Voronoi图创建

为了明确膨胀边界与原点之间的距离,使其更容易进行边界提取,采用一种基于正方形结构的距离结构元素,如图4所示。该结构元素原点为其几何中心,周边8个栅格表示距离原点距离为 1,第2层16个栅格表示距离原点距离为2,同时也表示为膨胀算子膨胀目标栅格的层数,该距离结构元素数学模型为:

其中,i,j为栅格编号;a,b为栅格距离参数。

图4 距离结构元素

基于膨胀运算使用距离结构元素对栅格地图进行处理,通过循环遍历地图上的每一个栅格,当栅格为空时使用式(3)对周围8个栅格进行扫描,如果周围有障碍物则根据式(3)计算值对该空栅格进行赋值,否则不对当前栅格进行操作,进行下一个栅格的运算。如下一个栅格已经有初始值,则不做处理继续扫描下一栅格。对栅格地图进行一次遍历,所涉及的障碍物都均匀膨胀一圈,再进行多次遍历后,整张地图无空闲栅格则膨胀运算结束。提取出每个障碍物的膨胀边界,从而组成了栅格Voronoi图[10]。

由于Voronoi图自身的数学属性,所确定的路径使移动机器人与障碍物之间的距离最大化,因此该路径对于移动机器人运动控制具有较高的可执行性。

3.4 双边界路径矢量化方法

2个相邻障碍物利用膨胀算子进行处理后,生成了2个并行的边界构成了栅格Voronoi图的路径,所以称该路径为双边界路径。所得到的边界移动机器人运动控制系统还无法识别,需要对其进行矢量化处理。

双边界路径矢量化方法采用2×2的栅格阵列作为检测窗口,对生成的栅格Voronoi图沿行、列方向进行扫描。扫描方式如图5所示,该图中栅格为栅格Voronoi图形成的双边界路径。i,j为栅格序号;x,y为栅格的长宽距离;栅格中的数字为距离结构元素膨胀障碍物时对栅格所赋的值。当2×2的栅格阵列中4个窗口均有值,则确定一个矢量坐标。而窗口有值数量小于等于3时,表明该点不是所求路径。当窗口扫描完整张栅格Voronoi图后,双边界路径矢量化结束。

图5 双边界路径矢量化方法

移动机器人运动控制系统在已知平台自身的位置后,输入目的地坐标来实现平台的运动。通过扫描整张栅格Voronoi图,并将栅格自身的横纵编号与预定的栅格长宽距离分别相乘,即得到了路径点横纵坐标,实现了路径矢量化。图5的双边界路径矢量化结果如图6所示。

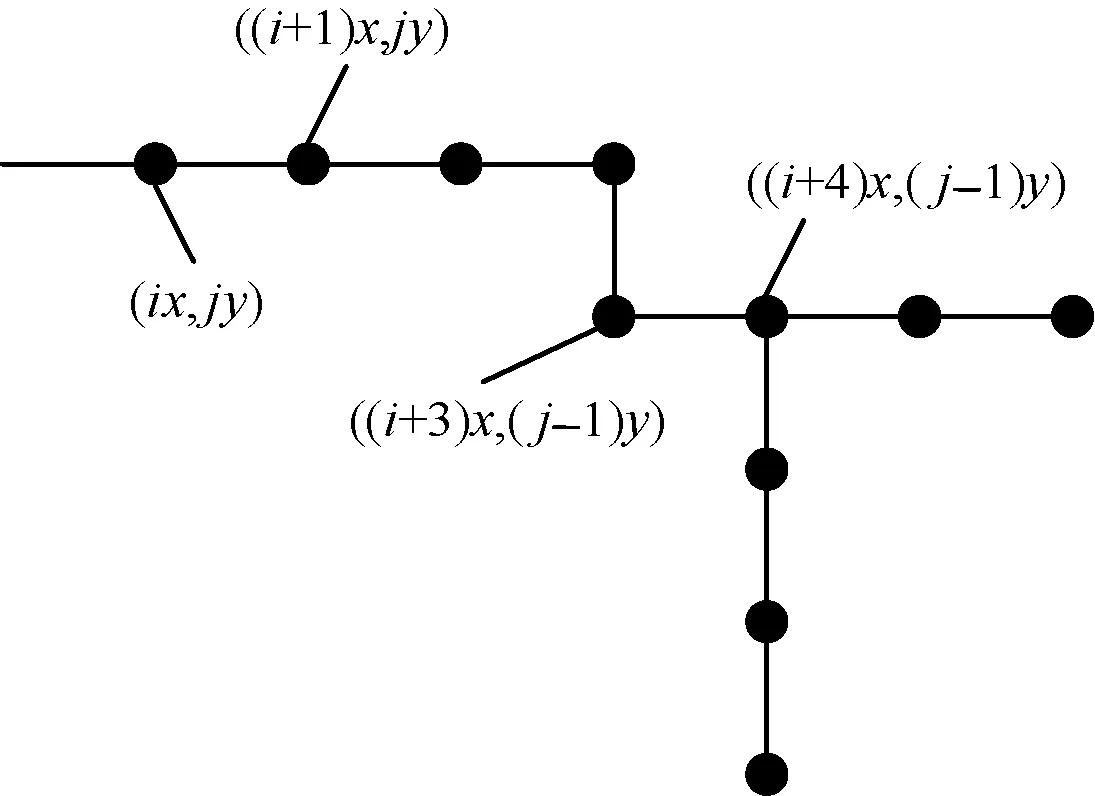
图6 路径矢量化结果

3.5 矢量路径拓扑化

拓扑路径所需的存储空间小,路径规划执行效率高,适合大规模与高精度地图环境下应用。由于所得到的矢量路径是以栅格地图为基础,因此在其点集的横纵方向上满足直线方程:

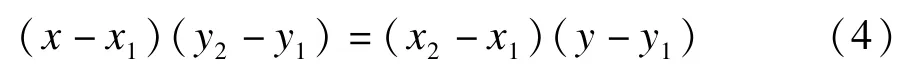
在地图中分别以行列方向进行扫描,在确定路径起始点后依次对后续点进行计算。栅格距离参数已知,当下一点距离小于等于该值时,则表示与上一点连续;当下一点距离大于该值时,则表示上一点为线段结束点,此点为下一线段的起始点。全图扫描结束后,记录所有直线端点坐标及起始点与结束点的连接关系,计算每条路径的长度,并对每一个节点重新编号,供后续路径规划使用。矢量路径拓扑化结果如图7所示,该方法去除了多余点,减少了数据冗余,实现了矢量路径的拓扑化[11]。

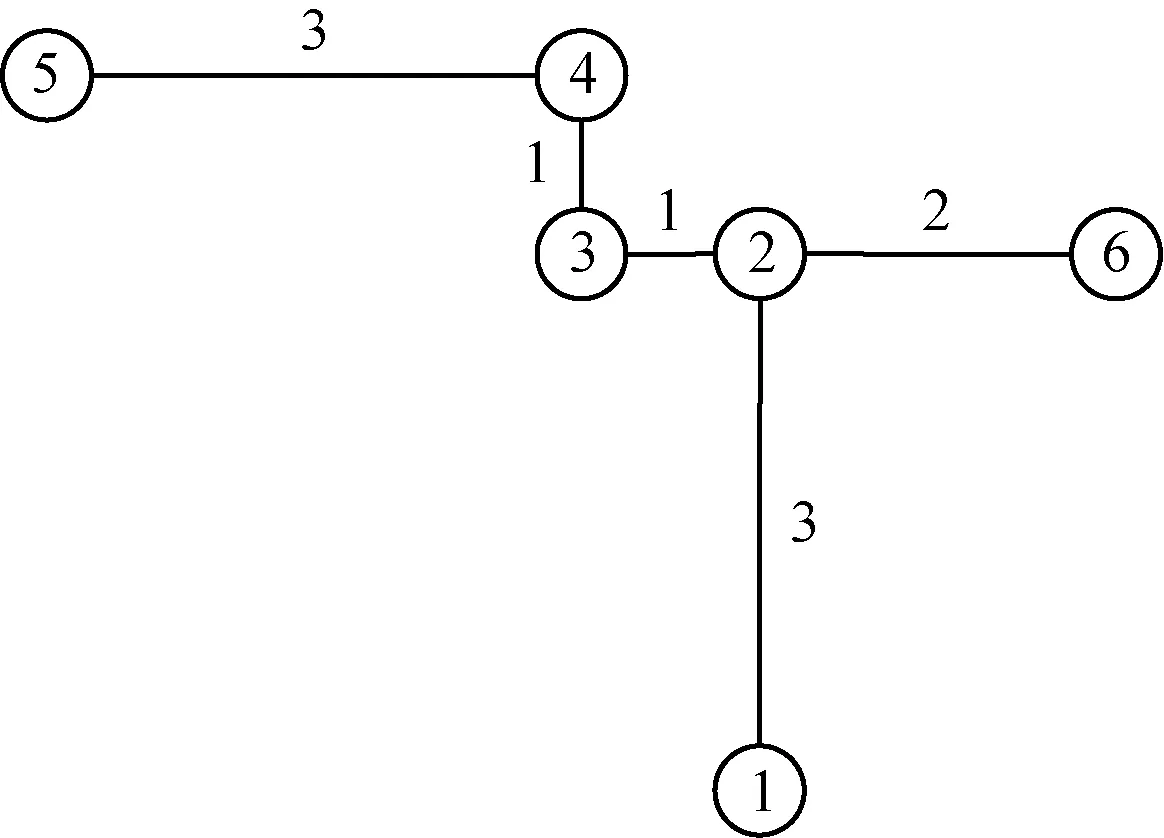
图7 拓扑路径

3.6 基于Dijkstra算法的路径规划

Dijkstra算法采用构造最小生成树的方法来进行路径规划,以起始点为中心向外搜索路径,直至到达终点为止,即计算出路径规划最优解。根据拓扑路径所提供的数据建立了路径网模型为:

其中,S为起始节点向量;E为终止节点向量;W为边权值向量,权值大小由所对应的边长度决定。将该三组向量保存为关联矩阵的稀疏矩阵形式,从而节省了地图存储空间。在路径网G中,存在的n个节点与m条边且每条边的权值为Wi,通过寻找从起始点到结束点的路径,使其各个边所对应的权值相加最小,则路径规划完成。路径规划算法步骤如下[12]:

(1)确定路径规划起始点与结束点;

(2)通过对路径网模型G的搜索,找到所有与待计算点直接连接的节点,并分别与之前计算的边权值进行累加,得到从起始点到所有找到点的权值集合:

(3)从权值集合中寻找最小值di=min{W1,W2,…},所得最小值点作为下一次搜索的待计算点。

(4)循环步骤(2)和步骤(3),直至所有节点计算完毕。

当路径规划结束后,得到一条由多个节点组成的最优路径。在矢量路径拓扑化过程中已经对节点的坐标进行了记录与编号,通过查表形式将各个节点的坐标按顺序发送给移动机器人运动控制系统,即完成了移动机器人的自主返航。

4 实验结果及分析

为验证本文提出的自主返航路径规划方法的可行性,建立二维15×15的栅格环境地图,地图中模拟了真实环境中的点、线和面等障碍物。图8所示是基于形态学膨胀算子的Voronoi图,图中黑色表示为障碍物。以障碍物为中心其边缘栅格依次变浅,可以看出每进行一次膨胀操作,所有障碍物都均匀膨胀一层,最终填满整张地图。

图8 基于形态学膨胀算子的Voronoi图

图9为基于方形距离结构元素的Voronoi图,图中栅格内的数据表示为该栅格距离障碍物的大小。

图9 基于方形距离结构元素的Voronoi图

图10为栅格Voronoi图边界及双边界路径矢量化的结果,图中有数字的栅格为Voronoi图的边界,可以看出每一个障碍物周围都由有一组完整的边界包围,2个相邻障碍物之间形成了双边界路径。利用双边界路径矢量化方法对边界进行处理,得到了图中的若干圆点,由于栅格距离参数为已知,因此每个圆点的坐标通过计算可以求得,从而生成了矢量路径网。

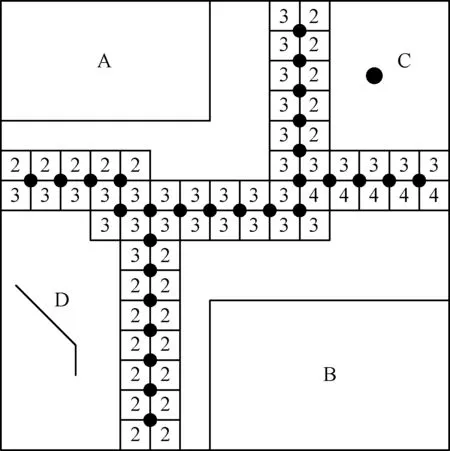
图10 栅格Voronoi图边界及双边界路径矢量化结果

图11为矢量路径的拓扑化及路径规划结果,利用所提出的矢量路径拓扑化方法对图10中的若干数据点进行处理,可以看出该方法去除多余圆点,并且保证了移动机器人运行轨迹不发生变化。图中圆圈数字是在拓扑化过程中对所提取的节点进行编号,Dijkstra算法需使用此编号进行路径规划。路径上的数字为该条路径的权值,也就是该路径的长度。基于Dijkstra算法的路径规划结果为①-②-⑥-⑦-⑨节点,规划出的路径由图中粗线表示。每个节点的坐标已知,则通过计算可以将该坐标直接发送给移动机器人运动控制系统,使机器人沿着预定路径行驶。观察路径所处位置可以看出该路径是机器人与障碍物之间的距离最大化,所以该路径对于移动机器人的运动具有较高的可执行性,减少了因定位精度问题发生碰撞的几率。

图11 矢量路径拓扑化和路径规划结果

图12为Dijkstra算法的加权图,该图中每条边关联一个权值,由若干节点与边权值组成了图模型。Dijkstra算法规划出从节点1-节点2-节点6-节点7-节点9的最小生成树。

图12 Dijkstra算法的加权图

5 结束语

遥控小型移动机器人在室内执行任务时需具有自主返航能力,但由于自身体积与载重能力限制使其自身定位能力较差,易与周围障碍物发生碰撞。本文提出了一种小型移动机器人自主返航路径规划方法,介绍小型移动机器人的任务流程,并设计了移动机器人的硬件系统。利用数学形态学中的膨胀算子对栅格地图中的障碍物进行膨胀运算得到了栅格Voronoi图。提出一种双边界路径矢量化方法对栅格Voronoi图进行处理,从栅格地图中提取出了矢量路径,并对该矢量路径进行拓扑优化,减少其冗余数据。通过Dijkstra算法对拓扑路径网进行路径规划并进行算法验证。实验结果表明,该方法所规划的路径使机器人与障碍物之间距离最大化,使移动机器人的运动轨迹具有较高的可执行性,减少了因定位精度问题发生碰撞的几率,实现了小型移动机器人在遥控信号丢失情况下的自主返航。

[1] 宋建梅,李 侃.基于A∗算法的远程导弹三维航迹规划算法[J].北京理工大学学报,2007,27(7): 613-617.

[2] 粱金泉,周之平,黎 明,等.基于关键链遗传操作的机器人路径规划[J].计算机工程,2012,38(9): 166-169.

[3] 宋 勇,李贻斌,李彩虹.递归神经网络的进化机器人路径规划方法[J].哈尔滨工程大学学报,2009, 30(8):898-902.

[4] 于振中,郑为凑,刘 鑫,等.基于Kinect的移动机器人实时局部路径规划[J].计算机工程,2013,39(4): 243-247.

[5] 刘利强,汪相国,范志超.基于小生境粒子群优化的船舶多路径规划方法[J].计算机工程,2013,39(9): 227-232.

[6] Roberge V,Tarbouchi M,Labonte G.Comparison of Parallel Genetic Algorithm and Particle Swarm Optimization for Real-time UAV Path Planning[J]. IEEE Transactionson IndustrialInformatics,2013, 9(1):132-141.

[7] 周 波,钱 来,孟正大,等.基于蚁群算法的喷图机器人路径排序优化[J].计算机工程,2012,38(1): 192-194.

[8] Birattari M,Pellegrini P,Dorigo M.On the Invariance of Ant Colony Optimization[J].IEEE Transactions on Evolutionary Computation,2007,11(6):732-742.

[9] Soile P.MorphologicalImage Analysis Principles and Applications[M].Berlin,Germany:Springer-Verlag,2002.

[10] Li C,Chen J,LiZ.A Raster-based Method for Computing Voronoi Diagrams of Spatial Objects Using Dynamic Distance Transformation[J].International Journal of Geographical Information Science,1999, 13(3):209-225.

[11] Thrun S.Learning Metric-topological Maps for Indoor Mobile Robot Navigation[J].Artificial Intelligence, 1998,99(1):21-71.

[12] 冯欣欣.Dijkstra算法在嵌入式 GIS中的优化实现[J].北京理工大学学报,2009,29(10):873-876.

编辑 金胡考

Path Planning Method in Autonomous Returning for Mini-mobile Robot

JIANG Tao,WANG Jianzhong,SHI Jiadong
(State Key Laboratory of Explosion Science and Technology,Beijing Institute of Technology,Beijing 100081,China)

Aiming at the existing problem of low locating accuracy of teleoperation mini-mobile robot in the actual application of autonomous returning,a path planning method in autonomous returning for mini-mobile robot is proposed. The task process and hardware system for mobile robot is introduced.The obstacle in grid map by dilation operator is calculated,and the grid Voronoi diagram is acquired.From the grid map extracts the vector path by method of double boundary,and the vector path based on topology optimization is optimized.The topology path employing the Dijkstra algorithm is planned.The experiments of path planning are carried out.The experimental results show that the path maximizes the distance between mobile robot and obstacle,and the motion trajectory of mobile robot has higher executability.The success rates of autonomous returning for mini-mobile robot are enhanced.

mobile robot;mathematical morphology;path planning;Voronoi diagram;topological optimization;Dijkstra algorithm

1000-3428(2015)01-0164-05

A

TP242

10.3969/j.issn.1000-3428.2015.01.030

国家部委基金资助项目。

姜 涛(1984-),男,博士研究生,主研方向:智能控制,无人作战平台;王建中,教授、博士生导师;施家栋,讲师。

2014-02-25

2014-03-30 E-mail:eli_jiang@126.com

中文引用格式:姜 涛,王建中,施家栋.小型移动机器人自主返航路径规划方法[J].计算机工程,2015,41(1):164-168.

英文引用格式:Jiang Tao,Wang Jianzhong,Shi Jiadong.Path Planning Method in Autonomous Returning for Minimobile Robot[J].Computer Engineering,2015,41(1):164-168.