一种交叉处理的混沌多变量Hash算法构造
张文婷,龙 敏
(长沙理工大学计算机与通信工程学院,长沙410014)
一种交叉处理的混沌多变量Hash算法构造
张文婷,龙 敏
(长沙理工大学计算机与通信工程学院,长沙410014)
在现有的并行处理模式下,Hash函数由于明文分块之间关联性不大从而引起安全问题。为此,提出一种交叉处理的多变量混沌Hash算法,算法安全性基于二次多变量多项式方程组求解问题(MQ问题)的困难性和混沌理论的复杂性。其中64个压缩函数可并行处理数据,利用多变量代数理论构造输出函数进一步混乱与扩散,根据不同的需求调整Hash值的长度。对算法分别进行存储空间分析、伪造攻击分析、差分攻击分析及统计实验分析,结果表明,该算法弥补了传统多变量多项式密码的运行效率不足,且可以抵抗伪造攻击、差分攻击和统计攻击。
Hash函数;MQ问题;混沌映射;交叉处理;并行模式
1 概述
Hash函数,也称散列函数、凑杂函数,用于将任意长度的消息压缩为固定长度的消息摘要。Hash函数广泛应用于数据完整性检测、身份认证、数字签名等领域。传统的Hash函数采用Merkle-Damgård结构,如经典的MD5[1]和SHA-1[2]算法。然而这类Hash函数的安全性能在文献[3-4]中被证实不可靠,且串行处理的结构导致效率不高,研究人员不再满足于传统Hash函数。
混沌是一种复杂的非线性动力学系统,它具有初值敏感性、随机性、长期不可预测性等性质,与密码学上扩散与混乱的要求一致,因此诞生了混沌密码学。近年来为了提高Hash算法的运行效率,新的混沌Hash算法越来越倾向于采用并行处理的模式。文献[5]提出了一种时空混沌的可并行处理Hash函数,文献[6]也成功地找到了该算法的碰撞。文献[7]利用分段线性函数和4维猫映射构造了一种可并行处理Hash函数,但文献[8]发现了该算法难以抵抗伪造攻击。尽管并行处理结构效率很高,但这种并行处理的结构导致明文的各分组之间联系不强,很容易遭受攻击。
有限域上MQ问题的求解是NP难解性问题,利用MQ问题构造密码可以抵抗量子计算机的威胁。2007年Billet等人首次将MQ问题应用到Hash函数中,提出了MQ-Hash[9]。然而这种基于多变量多项式方程组求解困难性的Hash函数存储空间巨大,运行速度缓慢,实用价值不高。而文献[10-11]也指出了直接利用MQ问题构造的多变量Hash函数的不足。
本文基于混沌映射和多变量多项式方程组构造了一种交叉结构的Hash算法,该算法利用并行Hash算法和多变量Hash算法的优点,抑制了两者分别容易遭到伪造攻击和差分攻击的缺陷。
2 预备知识
2.1 混沌映射
混沌是一种类似无规则、随机的运动,它对初值以及参数极其敏感,在长期内不可预测。这些性质都满足密码学中混乱与扩散的要求相符。本文采用Henon映射和分段线性映射来构造Hash算法。
(1)Henon映射

其中,当α=1.4,β=0.3时为典型Henon映射,典型Henon映射是混沌映射。Henon映射是二维混沌映射,它由xi,yi共同确定迭代方程,本文算法选择Henon映射生成密钥流,加大了算法的密钥空间。
(2)分段线性映射PLCM
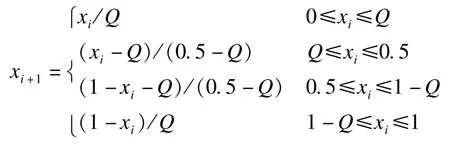
当x∈[0,1],Q∈(0,0.5)时,系统处于混沌状态。分段线性映射的分布均匀,且输出轨道的自相关函数是δ形的。同时它的形式简单,只有一个控制参数,易于实现且速度上有优势。本算法选择PLCM映射作为压缩函数。
2.2 MQ问题
给定一个有限域F=GF(q)上n个变量m个方程二次多项式方程组可以表示为:

其中,1≤i≤m,ai,j,k,bi,j,ci∈GF(q)。则MQ问题为如下所述,给定方程组f=(f1,f2,…,fm),每个分量fi都是有限域GF(q)上随机选择的n个变量的二次方程。对于已知的y∈Fm,求解一个x∈Fn,满足y=(f1(x),f2(x),…,fm(x)),叫做MQ问题。
MQ问题是NP难解性问题[12]。本文算法用二次多变量多项式结构作为输出函数,将前面并行的压缩函数隐藏起来,从而达到抵御伪造攻击的目的。
3 Hash函数的构造
3.1 消息填充
设明文的长度为m,Hash值的长度为n,明文被填充为512 bit的整数倍:在明文相应的二进制形式之后补充一个1,再补充若干个0。这段(100…0)2串的长度为l,满足(m+l)mod 512=512-16-64=432。然后在右边添加16 bit的Hash值长度n,最后再添加64 bit的消息明文长度m,如果m>264,则取mmod 264。
消息填充结构如图1所示。

图1 消息填充结构
3.2 算法描述
算法运算在由不可约多项式y8+y4+y3+1定义的GF(28)上,Hash值长度可取192 bit,224 bit, 256 bit,384 bit等。为描述方便,下文输出Hash值长度默认为192 bit。
(1)填充后的明文可分成s个512 bit的消息块M1,M2,…,Ms。对于每个消息块Mi(i=1,2,…,s)再分为64个子块Mi=block1,i,block2,i,…,block64,i,其中每个blockj.i为8 bit。对于所有blockj,i(j=1, 2,…,64)经下式线性变换后映射得到PLCM映射的参数Qj,i。

(2)算法的密钥为Henon映射的一对初值(xx,yy)。迭代Henon映射50次后选取后32对迭代值(xxη,yyη)(η=19,20,21,…,50)进行下式变换得到PLCM映射的初值。

这 64个 PLCM 映射的初值分别为key1,key2,…,key64,而系统参数是变化的,每轮系统参数取相应的Qj,i,(j=1,2,…,64;i=1,2,…,s),共迭代2s次。因这64个PLCM是并行处理的,所以每一路的操作一样,以PLCM1为例:PLCM1前s次迭代,参数依次为Q1,1,Q1,2,…,Q1,s;PLCM1后s次迭代,参数依次为Q1,s,Q2,s-1,…,Q1,1。这64个 PLCM构成交叉结构,即每一轮PLCMj生成的迭代值作为下一轮PLCMj+1的初值,而PLCM64的迭代值则作为下一轮PLCM1的初值。最后这64个PLCM同时得到64个终值,作为二次多变量多项式结构的输入。2s轮迭代之间的交叉结构如图2所示。
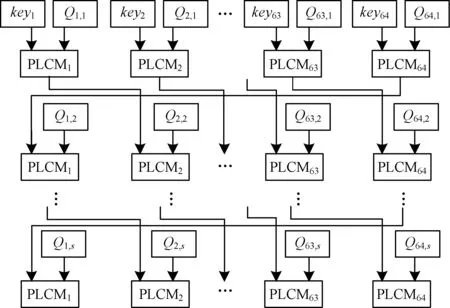
图2 压缩函数的交叉结构
(3)64个PLCM映射的终值作为二次多变量多项式方程组的 64个变量x1,x2,…,x64。此时GF(28)上64个变量24个方程的二次多变量多项式结构可表示为:

每个fk(k=1,2,…,24)都为如下形式:
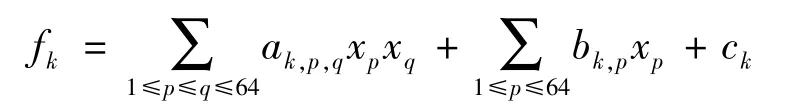
其中,ak,p,q,bk,p,ck都是从GF(28)上随机选择的元素。
这个二次多变量多项式结构将64个变量压缩为24个变量,而这24个变量级联起来得到最终192 bit的Hash值。算法的整体结构如图3所示。

图3 算法整体结构
4 性能分析与仿真结果
算法的压缩函数可定义为C=F(P(key,M)),其中,F为多变量多项式方程组;P为64路混沌映射;key为密钥;M为消息明文。设每轮函数Pi的结果为ρi=(ρ1i,ρ2i,…,ρ64i),要找到一对M≠M′,使得C(M)=C(M′),做如下证明:设第i轮时ρi=ρi′,i-1是满足ρi-1≠ρi-1′最大的情况,对于任意的ρi-1′计算得到ρi′=Pi(ρi-1′,Qi′),可推出Qi≠Qi′。假设第i轮后消息分组的值完全相同,则此后的迭代轨迹完全一致,在反向迭代至2s-i次时,再次使用Qi′作为参数计算得到 ρ2s-i+1′=P2s-i(ρ2s-i′,Qi′),由于Qi≠Qi′,ρ2s-i=ρ2s-i′而可推出 ρ2s-i+1≠ρ2s-i+1′。 那么对于往后2s-i+1至2s轮迭代,根据混沌的性质,其轨迹仍然将会截然不同,从而导致F的计算结果不同,即C(M)≠C(M′),因此可以认为算法是无碰撞的。混沌的运动十分复杂,对初值极其敏感,对明文任意微小的改变都会导致迭代值极大的变化,即使在攻击者已知P2s的最坏情况下,求解F也是不可行的,因为F是个NP难解性问题,从而保证了算法的单向性。
4.1 存储空间
整个算法由混沌迭代和多变量多项式计算2个部分组成。第一部分所需存储空间主要是PLCM映射的状态值和系统参数,而迭代64个PLCM映射2s次需64×2s×(2×8)bit。第二部分为有限域GF(28)上的二次多变量多项式方程组,其所需存储空间主要是有限域GF(28)的乘法表和随机系数。GF(28)有256个元素,每个元素8 bits,则乘法表需要256×256×8 bit。多变量多项式方程组有nm(n+l)/2个二次项,nm个一次项和m个常数项。表1列出不同Hash值长度情况下MQ部分所占存储空间。

表1 二次多变量多项式结构所占存储空间
混沌部分所占空间由明文大小决定,多变量多项式部分的存储空间则是固定的。因迭代Henon映射50次产生的密钥流所占空间极小,此处计算忽略。因此,算法的存储空间主要由明文大小和多变量多项式的随机数决定。一段大小为512sbit(s为明文分组数)的明文在Hash值长度为192 bit的情况下,多变量多项式结构占114.27 KB混沌部分占0.25sKB,共计114.27+0.25sKB。显然,与占用将近3.5 MB的MQ-Hash[9],本算法在存储空间上具有明显优势。这是因为MQ-Hash的采用的传统的串行处理结构,每个压缩函数中都要对当前明文分组进行一次多变量多项式计算,而本文的压缩函数为并行的混沌映射而多变量多项式方程组为输出函数,对于任意长度的明文仅作一次多变量多项式计算。
4.2 抗伪造攻击性
伪造攻击是指给定一段消息,攻击者不知其密钥的情况下根据该消息的Hash值来构造明文,从而达到攻击的目的。文献[6,8]中指出并行处理的结构导致明文的各分组之间联系不紧密,因而无法抵御伪造攻击。因此,本算法在并行运算前,对明文的每个分组做了如下线性变化来加强各分组的联系:

该变换由3个位置因素决定:当前消息块的横向坐标i、当前消息块的纵向坐标j和消息块的总数s,增减修改明文的任何数据都会不同程度地改变i,j,s,从而改变了Qi,j的值。同时算法又引进了交叉处理,当前混沌映射处理后得到的迭代值在下一轮中并不由自身处理,而是送给相邻的混沌映射处理,这样大大加强了明文不同分组之间的联系,中间值微小的变化会在最终的Hash中放大,使得明文充分混淆。此外算法在并行的压缩函数之后,用二次多变量多项式结构作为输出函数。对于文献[6,8]中提出的将上下两行Hash值交换后进行异或运算而产生相同结果的攻击方法,由于本算法中多变量多项式结构进一步对并行处理结构的结果充分置乱,隐藏起压并行处理结构的内部状态,从而不再可行。
4.3 抗差分攻击性
MQ问题是NP难解性问题。但是解决MQ问题的复杂度取决于方程数m,变量数n和有限域的阶q。现已存在有效地解决超定多变量多项式方程(n<m)的方法和置换多变量多项式方程(n=m)的方法,因此在利用多变量多项式构造密码时通常使用不定方程(n>m)。本算法在选择Hash值长度为192 bit,224 bit,256 bit,384 bit时,多变量多项式结构均可表示为F64→F24,F64→F28,F64→F32和F64→F48的不定方程形式。相比求解复杂度为O(qm)的穷举攻击,文献[13]中提出一种复杂度大大降低的解决不定方程系统的算法:设,当k满足2k2>m-2k时,该算法的复杂度为O(qm-k)。可见利用该算法有效求解二次多变量不定方程,对不定方程的取值要严格的限定,该算法仅适用于q,n,m很小的情况。按照文献[13]的求解方法在不同的Hash值长度情况下解决本算法MQ问题部分的复杂度在表2列出,可见本文算法的二次多变量多项式结构理论上不可解。

表2 二次多变量多项式结构的求解复杂度
设Q为有限域F上m个方程n个变量的二次方程组为f1,f2,…,fm。对于任意给定的 δ=(δ1, δ2,…,δn)可在多项式时间O(mn2)内找到一对输入x=(x1,x2,…,xn),y=(y1,y2,…,yn)发生碰撞,其中,(x,y)=(x,x+δ)[9]。单独使用二次多变量多项式来构造密码是不安全的,无法抵御差分攻击。
差分攻击的是针对分组通过分析明文对的差值对密文对的影响来恢复部分密钥,而本文算法中明文的各分组在经多变量多项式结构处理前先经过交叉的64组混沌映射处理,经多轮迭代将初始值扩散到整个相空间,这种对明文充分的置乱很难从最终的迭代值中推算原始消息。而要在本文算法的二次多变量多项式结构部分发现碰撞,必须要求前面的压缩函数部分可逆,而压缩函数采用的混沌映射的性质确保了在输入差分经过数次迭代已均匀分布到所有比特位,因此,在二次多变量多项式结构寻找碰撞是不可行的。
4.4 统计分析
4.4.1 扩散与混乱性质测试
Shannon引入了扩散与混乱2个概念来评估密码系统的性能。对于用二进制表示的Hash值,每1 bit只有0或者1两种可能,因此理想的Hash值扩散效果应该是明文中1 bit变化会引起Hash值50%的变化。

其中,N为统计次数;Bi为第i次测试变化的位数;h为Hash值的长度。
取密钥 xx=1.17,yy=-0.28。对初始文本“Hash function is an algorithm converts variable length message to a fixed length of digest,which is called hash value.Hash function has a wide range of application in information security,such as data integrity authentication, identity authentication and digitalsignature.”进 行1 000次测试,每次随机改变文本中1 bit的值,并比较改变后的Hash值和原始文本的Hash值。不同Hash值长度下1 000次测试相应的平均变化比特数、平均变化概率P、均方差ΔB、均方差ΔP在表3中列出。

表3 雪崩测试统计结果
4.4.2 Hash值分布
安全的Hash算法的一个重要要求是Hash值均匀分布。本文对以下消息进行仿真实验:“Hash function is an algorithm converts variable length message to a fixed length of digest,which is called hash value.Hash function has a wide range of application in information security, such as data integrity authentication,identity authentication and digital signature.”密钥取 xx=1.17,yy=-0.28。通过仿真结果可以看到明文与Hash值的分布:图4(a)为明文的ASCII码值分布图,ASCII码值集中地分布在90~120这个范围内;而图4(b)为十六进制Hash值的分布图,Hash值分布十分分散。由此可知,本文算法得到的Hash值有良好的扩散与混乱性能。

图4 明文和Hash值的分布
4.4.3 敏感性分析
为测试本文算法对于明文和密钥的敏感程度,在7种不同条件下对4.5.1中的文本进行仿真实验。
文本1:原文。
文本2:将原文首字母H改为G。
文本3:将原文中as一词改为is。
文本4:将原文末尾处句点改为逗号。
文本5:在原文末尾添加一位空格。
文本6:将 密 钥yy取 值 由 -0.28改 为-0.280 000 000 000 000 1。
文本7:将 密 钥xx取 值 由 1.17 改 为1.170 000 000 000 000 1。
仿真所得192 bit的Hash值长度的十六进制形式如下:
文本1:BAD4A890BF7240044C22B58E0A45A1C598 6D2E67E65A9939
文本2:27F08D4ECBC371221D35193A4D797391E4 CE56077B0A26D5(改变94位)
文本3:0BC2E9D74577C01E611F6480C51C63F43E CCC5DD136CFB7F(改变91位)
文本4:0F034E33295F561EF088BFF984B55ED96989 CC988750FE02(改变106位)
文本5:CEE066D48D20D8F2DA3C1924A69539735 C39FC711CA64547(改变96位)
文本6:400543850934F5EB02D3797DB6BB53CBE2 F06E62CF721A02(改变104位)
文本7:F093000A8363508DD75F621B782CEA4A6C 6D6397C30A546D(改变88位)
图5所示为相应的Hash值二进制形式的图形分布,可以看出对明文和密钥的任何细微改变都会对Hash值产生巨大的影响,证明算法对明文和密钥的敏感程度良好。

图5 7种条件下二进制Hash值比较
5 结束语
本文结合混沌理论的复杂性和MQ问题的难解性,提出一种新的交叉迭代的Hash算法,算法占用空间小、处理速度快,另外,可根据不同需求调节Hash值长度。仿真实验和理论分析证明本文算法满足Hash算法的安全要求,且具有处理大容量数据的潜力。今后的工作重点是以该算法为基础研究在云端进行消息认证的方法。
[1] Rivest L.The MD5 Message digest Algorithm[S]. RFC 1321,1992.
[2] NIST.FIPS PUB 180-2-1993 SecureHash Standard[Z].1993.
[3] Wang Xiaoyun,Yu Hongbo.How to Break MD5 and Other Hash Functions[C]//Proceedings of EUROCRYPT’05. Berlin,Germany:Springer-Verlag,2005:19-35.
[4] Wang Xiaoyun,Yu Hongbo.Finding Collisions in the Full SHA-1[C]//Proceedings of EUROCRYPT’05. Berlin,Germany:Springer-Verlag,2005:17-36.
[5] 赵 耿,徐 刚,闵乐泉.一种并行时空混沌单向Hash函数的构造[J].微计算机信息,2011,27(5):232-236.
[6] 王 浩.混沌单向Hash函数的安全性分析研究[D].长沙:长沙理工大学,2013.
[7] Xiao Di,Liao Xiaofeng,Dong Shaojiang.Parallel Keyd Hash Function Construction Based on Chaotic Maps[J]. Physic Letters A,2008,17(7):2388-2393.
[8] Xiao Di,Liao Xiaofeng,Wang Yong.Improving the Sec Urity of a Parallel Keyd Hash Function Based on Chaotic Maps[J].Physic Letters A,2009,373(36):4346-4353.
[9] Olivier B,Matt R,Homas P.On Building Hash Functions from Multivariate Quadratic Equations[C]//Proceedings of ACISP’07.Berlin,Germany:Springer-Verlag,2007: 82-95.
[10] Ding Jintai,Yang Boyin.Multivariates Polynomials for Hashing[EB/OL].(2007-10-21).http://eprint.iacr. org/2007/137.pdf.
[11] Pierre-Alain F,Louis G,Jacques S.Differential CryptanaLysis for Multivariate Schemes[C]//Proceedings of EUROCRYPT’05.Berlin,Germany:Springer-Verlag,2005: 341-353.
[12] Garey T,Johnson D.Computers and Intractability,A Guide to the Theory of NP-completeness[M].New York,USA: [s.n.],1979:128-130.
[13] Nicolas C,Louis G,Jean-Daniel T.Solving Underdefined Systems ofMultivariate Quadratic Equations[C]// Proceedings of PKC’02.Berlin,Germany:Springer-Verlag, 2002:211-227.
编辑 索书志
Chaos Multivariate Hash Algorithm Construction of Cross Processing
ZHANG Wenting,LONG Min
(College of Computer and Communication Engineering,Changsha University of Science and Technology,Changsha 410014,China)
Aiming at the defects of security in the existed parallel Hash funtions which are caused by the weak correlations between the plaintext block,a novel Hash function algorithm based on the difficulty of solving MQ problem and the complexity of chaotic theory is proposed.The algorithm works in a parallel and cross processing mode.The output function is constructed by multivariate polynomials equations to confuse the plaintext sufficiently.The output Hash size can be adjusted according to different requirements.Storage analysis,forge attack analysis,differential attack analysis and statistic analysis are carried on algorithm.Theoretical analysis and experimental results show that the parallel structure of the algorithm compensates the inefficiency of traditional multivariate polynomial cryptosystems,and it can resist forge attack,differential attack and statistic attack.
Hash function;MQ problem;chaotic mapping;cross processing;parallel mode
1000-3428(2015)01-0130-05
A
TP309
10.3969/j.issn.1000-3428.2015.01.024
国家自然科学基金资助项目(61001004);湖南省教育厅基金资助项目(11B002);湖南省海外名师基金资助项目(2013008);湖南省研究生科研创新基金资助项目(CX2013B376)。
张文婷(1989-),女,硕士研究生,主研方向:单向Hash函数;龙 敏,教授、博士。
2014-03-03
2014-04-03 E-mail:yesterdayjuly@qq.com
中文引用格式:张文婷,龙 敏.一种交叉处理的混沌多变量Hash算法构造[J].计算机工程,2015,41(1):130-134.
英文引用格式:Zhang Wenting,Long Min.Chaos Multivariate Hash Algorithm Construction of Cross Processing[J]. Computer Engineering,2015,41(1):130-134.

