多用户MIMO系统中一种自由度分配算法

高 慧,周欣瑞,吴仁铭,朱 谦

(1.复旦大学信息科学与工程学院,上海200433; 2.国立清华大学通讯工程研究所,中国台湾新竹30013)

·移动互联与通信技术·

多用户MIMO系统中一种自由度分配算法

高 慧1,周欣瑞2,吴仁铭2,朱 谦1

(1.复旦大学信息科学与工程学院,上海200433; 2.国立清华大学通讯工程研究所,中国台湾新竹30013)

近年来迭代干扰对齐技术得到了较多的关注,通过迭代干扰对齐算法可设计线性预编码矩阵,以最大化多输入多输出系统的总速率。但目前将自由度(DoF)分配方式作为系统总速率影响因素的研究较少。为此,提出一种DoF分配算法,通过改进模拟退火算法从而得到可使系统总速率达到最大的DoF分配方式。DoF分配问题是组合优化问题,采用模拟退火算法可较好地解决该问题。仿真结果表明,该算法所获得的系统总速率接近遍历算法的性能,具有更低的复杂度。尤其当系统变得复杂(用户数目增加,或者天线数目增加)时,改进模拟退火算法的低复杂度优势更为明显。

多输入多输出;迭代干扰对齐;自由度分配;模拟退火算法;总速率

1 概述

多输入多输出(Multiple-input Multiple-output, MIMO)技术可以在不增加发射功率和不占用更多频率资源的情况下,极大地提高系统总速率。因此,自被文献[1-2]提出以来,已成为无线通信领域的研究热点。对于多用户MIMO系统,当天线数目及用户数量增加时,多用户干扰会成为制约系统总速率增加的重要因素[3],这点可通过干扰对齐技术解决。

干扰对齐作为一种有效的干扰管理技术[4],由于能够显著提高系统总速率,因此受到了广泛关注[5-6]。它最先由文献[7]提出,通过在接收方给干扰信号分配一部分可用的资源(时间,频率,空间)使得所有干扰项目被压缩在这部分空间。此外,文献[8]已经证明:干扰对齐技术可使得多用户MIMO干扰信道的自由度达到最大。

前人的研究大都是从消除干扰的角度使得多用户MIMO系统获得最大总速率,却忽视了自由度(Degree of Freedom,DoF)分配对系统总速率的影响。本文基于迭代干扰对齐(Iterative Interference Alignment,IIA)技术[9]探索一种使多用户MIMO系统的总速率最大化的具有低复杂度的DoF分配优选算法。

对多用户MIMO干扰信道做DoF分配事实上是一种组合优化问题。该类问题即是解决具有很多独立变量的函数的最大值或最小值问题。对于组合优化问题,直观的方式是通过遍历法(Exhausting search,EX)搜寻所有可能解,从而选出最优的DoF分配策略。然而,很多组合优化问题实质上是NP完全问题[10],得到精确解所需的收敛时间随着问题的规模增加呈指数增长。因此,运用启发式算法来解决此类NP完全问题是一种行之有效的方法。

模拟退火算法是一种启发式的全局优化算法,已被应用到许多领域。它可以在一个可接受的收敛时间内给出一个满意的次优解,相比遍历算法大大减少了算法的复杂度及收敛时间。

本文基于迭代干扰对齐[9]技术,旨在通过改进的模拟退火算法搜索到可使多用户MIMO系统总速率最大的DoF分配方案。

2 K-user MIMO干扰信道模型

图1描述了K-user MIMO干扰高斯信道模型, K-user MIMO干扰信道由K对发射机-接收机组成,每个发射机具有M根天线,每个接收机具有N根天线。假设信道参数与时间和频率无关,一个发射机只与与其匹配的接收机发送信号,对于其他接收机而言,该信号是干扰信号。接收机k的接收信号表达如下:

其中,yk表示接收机k收到的信号;Hk,l是接收机k与发送机l之间的平坦衰落信道矩阵;Fl与nl表示预编码矩阵和满足正态分布的N(0,N0I)加性高斯白噪声;sk是发射机k传送给接收机l的信号向量。

令Ω表示所有可能的DoF分配方式的集合,即K-user MIMO干扰信道的DoF域。Si=[s1,sk,…,sK]表示一种具体的DoF方案,其中,sk表示用户k被分得的DoF数目。

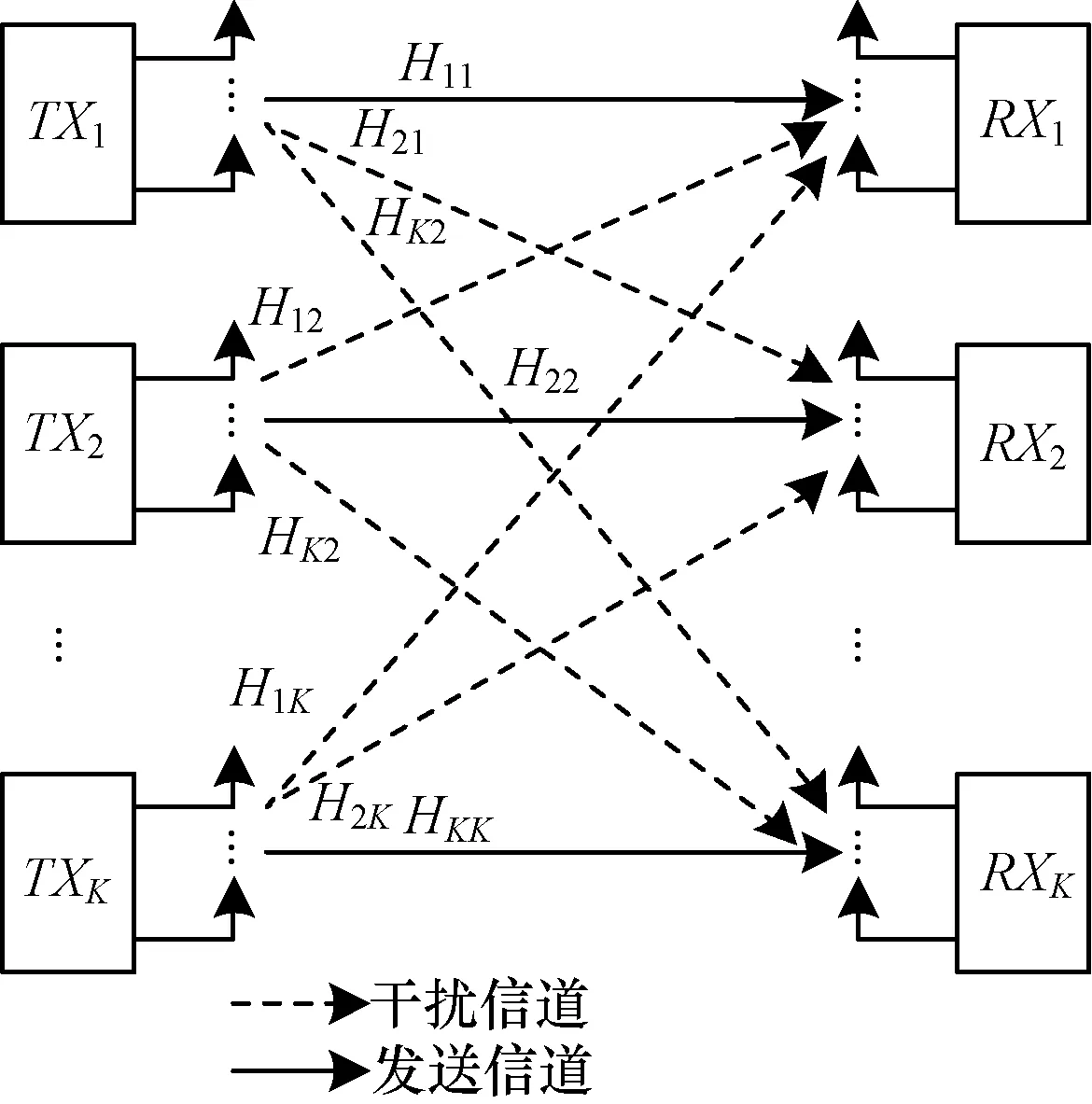
图1 K-user MIMO干扰高斯信道

因此可将问题描述如下:让C:Ω→R表示定义在DoF域上的目标函数(即K用户MIMO干扰信道的总速率),目标是找到一种最佳的DoF分配方式S∗,使得对于任意一种 DoF分配方式Si,都有C(Si)＜C(S∗)。

文献[11]已经证明对于K-user MIMO干扰系统,当K≤R时,总自由度数目可以达到min(M,N)K;而当K＞R时,总自由度数目为,其中,。因此,DoF搜索域Ω为:

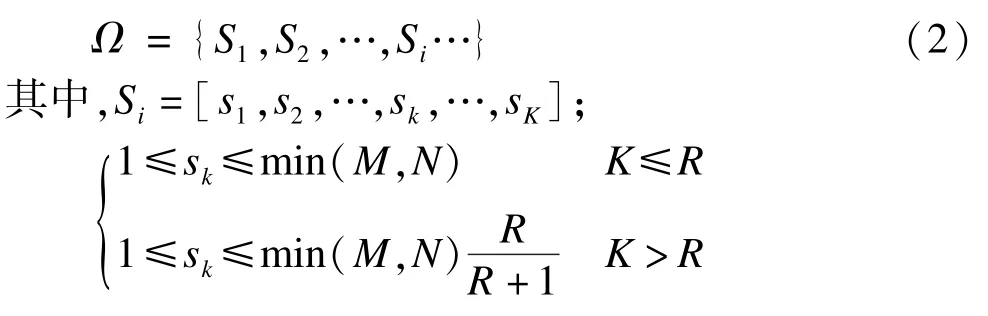
由于min(M,N),本文选取一个较大的上限:min(M,N)。

此外,在文献[9]提出的迭代式的干扰对齐算法可在不用考虑用户数目、获得CSI的方式以及DoF的分配下获得预编码Fl与干扰空间的正交基Ck,从而将干扰信号压缩在部分自由度上。

因此,K-user MIMO干扰高斯信道的总速率可以表达如下:

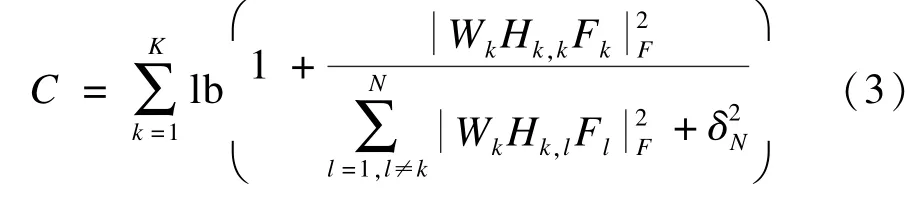
其中,Fl表示发送机的预编码;Wk表示接收信号空间的正交基(表示接收机干扰空间的正交基,是Ck的共轭转置矩阵);与分别表示WkHk,kFk与WkHk,lFl的Frobenius范数。

综上所述,可将寻求K-user MIMO系统的最大总速率问题表述为:

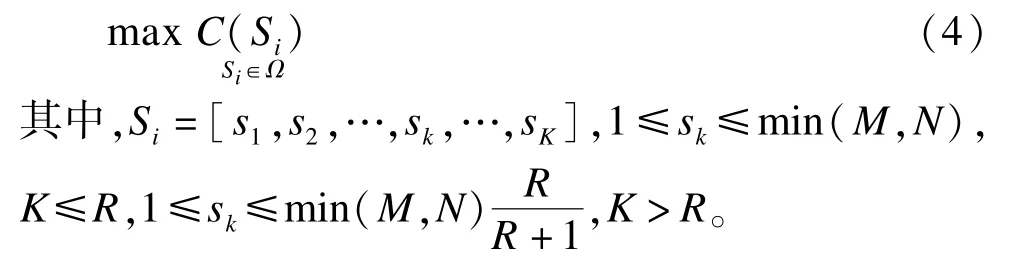
3 基于模拟退火算法与IIA的DoF分配

模拟退火的概念源自一个特殊的领域:统计物理学[12]。退火过程如下:为使一块固体物质达到最低能量基态,首先将其加温至其粒子可自由移动,然后徐徐的降温,粒子会逐渐形成低能级晶格。若降温速度足够慢,固体物质必会达到最低能量的基态。类似的,将不同的DoF分配方式Si看做固体物质中的每一个粒子,将对应的K-user MIMO系统的总速率C(Si)看做固体物质的能量函数,通过缓慢减少模拟温度进行迭代优化,则可使系统的总速率最终达到最大。

本文旨在找到K-user MIMO干扰系统总速率的最大值,有必要对退火算法中的Metroplis概率接受准则做些调整。做法如下:

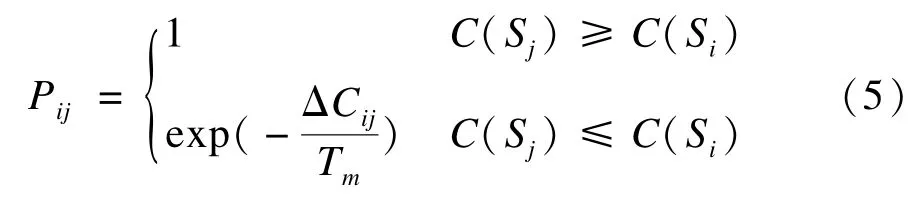
其中,Pij为状态接受概率,即表示状态Si产生Sj后,接受Sj作为新状态的概率;ΔCij表示总速率的增量, ΔCij=C(Sj)-C(Si);Tm为退火温度,m为迭代次数;C(Si)为K用户MIMO系统的总速率;Si表示DoF分配方式,Si∈Ω。

除了概率接受准则,模拟退火算法还需要其他4个重要的因素:

(1)解空间:所有的DoF分配策略,用集合Ω表示,见式(2)。

(2)新解产生函数:候选解一般按照某一概率密度分布函数对解空间进行随机采样所得,本文中选取平均密度分布函数从Ω中对DoF分配策略采样。

(3)目标函数:K-user MIMO系统所获得的最大总速率,见式(3)。

(4)冷却进度表:温度控制着整个退火过程,包括初始温度、降温因子及退火终止条件。

1)初始温度:设为T0,应足够高以便所有的可行解都能被遍及。然而温度越高意味着收敛速度越慢。事实上它是一个经验值;

2)降温因子:设为r,直接控制了退火算法的收速度,Tm+1=r×Tm(0＜×＜1);

3)终止条件:包含特定温度(Tm)下热平衡判决条件(内循环)及退火过程的终止判断(外循环)。在Tm下,如果最新几次所获得的目标函数的值的方差在[0,ξ]内变化,则认为系统在Tm下已达到热平衡。ξ是一个很小的正整数(本文取ξ=0.01)。对于退火过程的终止,如果最新所获得的一些目标函数值(在极低的几个温度下)“足够平坦”,即目标函数值均方差在[0,ε]内浮动(本文中ε=0.01),则认为退火结束。

以上的设计思想充分表述了模拟退火算法。然而在温度不为0℃时,跳出区域最优解总有可能会发生。最终得到的解可能不是最优的,因为模拟退火算法是一种概率算法。因此,有必要对模拟退火算法做一些改进以便增加获得最优解的概率。

本文为避免搜索过程中由于执行概率接受环节而遗失当前遇到的最优解,增加了存储环节,将每个Tm温度下获得的最优解记忆下来。待退火过程结束后,从中选取出最大值作为最优解。

基于模拟退火算法及干扰对齐技术,可使K-user MIMO系统的总速率达到最大,DoF分配流程如图2所示。

图2 基于模拟退火的K-user MIMO系统DoF分配流程

该算法具体步骤如下:

(1)选取模拟退火算法的初始温度T0,退火系数r。

(2)从解空间Ω中选取一组DoF分配Sj,计算系统总速率C(Sj)及其改变量ΔCij=C(Sj)-C(Si)。若ΔCij≤0,或者exp(-ΔCij)＞random(0,1)则接受新状态Sj令Si=Sj;否则保持Si状态。

(3)如果在该温度下达到内循环收敛准则,转到步骤(4);否则转到步骤(2)。

(4)先保存“中间最优解”,然后执行外循环收敛准则,若满足则退火过程结束,跳至步骤(5);否则继续降温:Tm+1=r×Tm,转至步骤(2)。

(5)从迭代过程中遇到的所有“中间最优解”中,选出最佳解,退火过程结束。

4 实验结果及算法复杂度分析

本节给出以下仿真结果来验证模拟退火算法的性能。在本文实验中,K=4,SNR是常量。

图3刻画了SA-IIA算法的收敛过程(M=8,N=7,SNR=60 dB,T=30,r=0.9)。在开始时,目标函数值的幅度跳跃很大,这点可由Metropolis算法解释:在温度较高时,从最佳值跳到较次的值的概率很大。随着温度降至0°C,这种概率也几乎为0。最终在温度趋于0°C时,系统总速率收敛到最优解。

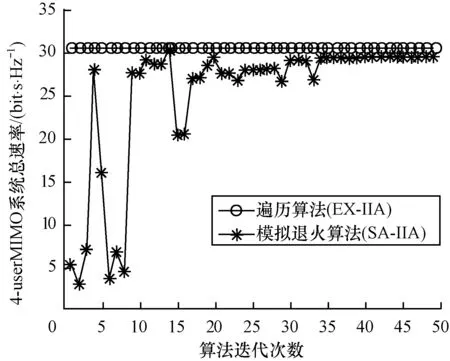
图3 模拟退火算法的性能

本文中SA-IIA算法得到的收敛解是30.36,同最优解一致;在收敛时间方面,SA-IIA是80.8 s,而EXIIA是317.2 s,因此收敛时间大致是EX-IIA的1/4。

需要说明的是,本文SA-IIA算法在迭代第14次时,搜索到了最优解。如若未采用“Best So Far”最终的收敛解是29.36。由此可见,补充搜索确实提高了收敛解的质量。

表1给出了不同天线数目下SA-IIA与EX-IIA的计算量比较,清晰地表明了SA-IIA在计算复杂度上的优势。事实上,exhausting search的计算次数是可以预期的。观察式(3),执行exhausting search所需的计算次数为min(M,N)K。对于SA-IIA虽然每次收敛次数并不固定,但是可以由内外循环次数控制。

表1 模拟退火算法与遍历法的计算量比较

5 结束语

本文基于模拟退火算法与迭代干扰对齐算法,提出一种DoF分配方法,即改进模拟退火算法。该算法可以大大降低计算复杂度,缩减收敛时间,并给出一个可满足需要的次优解。并且当用户数目增加或者天线数目增加时,本文算法的计算复杂度具有明显的优势。

[1] Foschini J G,GansM J.On LimitsofWireless Communications in a Fading Environment when Using Multiple Antennas[J].Wireless Personal Communications,1998,6(3):311-335.

[2] Emre T.Capacity ofMulti-antenna Gaussian Channels[J].European Transactions on Telecommunications, 1999,10(6):585-595.

[3] Shyamnath G,David P S,Dina K.Interference Alignment and Cancellation[J].SIGCOMM Communi-cation Review,2009,39(4):159-170.

[4] Shen H,Lin B,Luo Y,et al.Iterative Minimum Mean Square Error Interference Alignment Scheme for the MIMO X Channel[J].IEICE Transactions on Communications,2011,94(5):1348-1354.

[5] Nosrat M B,AndrewsJG,HeathR W.MIMO Interference Alignment over Correlated Channels with Imperfect CSI[J].IEEE Transactions on Signal Processing,2011,59(6):2783-2794.

[6] 王勤民,张忠培,常青美,等.干扰信道中一种权值可调的迭代算法[J].电子与信息学报,2012,34(12): 2850-2854.

[7] Maddah-Ali M A,MotahariA S,KhandaniA K. Signaling over MIMO Multi-base Systems:Combination of Multi-access and Broadcast Schemes[C]//Proceedings of IEEE International Symposium on Information Theory.Seattle,USA:[s.n.],2006:214-222.

[8] Cadambe V R,Jafar S A.Interference Alignment and the Degrees of Freedom for the K User Interference Channel[J].IEEE Transactions on Information Theory,2008, 54(8):3425-3441.

[9] Peters S,Heath R W.Interference Alignment via Alternating Minimization[C]//Proceedings of ICASSP’09.[S.1.]: IEEE Press,2009:159-167.

[10] Reingold E M,NievergeltJ,Deo N.Combinatorial Algorithms:Theory and Practice[M].Englewood Cliffs, USA:Prentice-Hall,1977.

[11] Gou Tiangao,Jafar S A.Degrees of Freedom of the K UserM×NMIMO Interference Channel[J].IEEE Transactions on Information Theory,2010,56(12): 6040-6057.

[12] Kirkpatrick S,Gelatt C D,Vecchi M P.Optimization by Simulated Annealing[J].Science,1983,220(4598): 671-680.

编辑 索书志

A Degrees of Freedom Allocation Algorithm in Multi-user MIMO System

GAO Hui1,CHOU Hsin Jui2,WU Renming2,ZHU Qian1
(1.School of Information Science and Technology,Fudan University,Shanghai 200433,China; 2.Institute of Communications Engineering,National Tsinghua University,Hsinchu 30013,Taiwan,China)

This paper considers the joint interference alignment and allocation of Degrees of Freedom(DoF)in multiple access K-user Multiple-Input Multiple-Output(MIMO)interference channel to maximize the sum capacity. Because a set of linear precode and corresponding combining matrices can be designed to maximize the sum rate,while joint consideration of sum capacity and distribution of DoF is less addressed.Therefore,this paper proposes an improved DoF allocation algorithm to search ideal DoF allocation which can maximize the sum rate.The essence of DoF allocation is a combinational optimization problem.SA algorithm has notable advantage over this.Simulation results show that the proposed modified SA algorithm achieves sum rate performance near that of the Exhausting search(EX)asymptotically, while the SA has lower computation complexity.Especially,when the system becomes more complicated(increasing user numbers or antennas),the low complexity advantage of SA algorithm is much more notable.

Multiple-input Multiple-output(MIMO);Iterative Interference Alignment(IIA);Degrees of Freedom (DoF)allocation;Simulated Annealing(SA)algorithm;sum-rate

1000-3428(2015)01-0071-04

A

TP391

10.3969/j.issn.1000-3428.2015.01.013

高 慧(1989-),女,硕士,主研方向:无线通信,MIMO技术,无线传感器网络;周欣瑞,博士;吴仁铭、朱 谦,副教授。

2014-01-24

2014-03-06 E-mail:huigao11@fudan.edu.cn

中文引用格式:高 慧,周欣瑞,吴仁铭,等.多用户MIMO系统中一种自由度分配算法[J].计算机工程,2015, 41(1):71-74.

英文引用格式:Gao Hui,Chou HsinJui,Wu Renming,et al.A Degrees of Freedom Allocation Algorithm in Multi-user MIMO System[J].Computer Engineering,2015,41(1):71-74.