受限模糊网络可信近邻查询

高 峻,郝忠孝,2

(1.哈尔滨理工大学计算机科学与技术学院,哈尔滨150080;2.哈尔滨工业大学计算机科学与技术学院,哈尔滨150001)

受限模糊网络可信近邻查询

高 峻1,郝忠孝1,2

(1.哈尔滨理工大学计算机科学与技术学院,哈尔滨150080;2.哈尔滨工业大学计算机科学与技术学院,哈尔滨150001)

针对不确定网络环境下的近邻查询问题,给出一种新的解决方法。将不确定网络建模为模糊图,定义模糊图中两点间的可信最短路径距离和可信最短路径期望距离,在可信距离基础上,提出模糊图可信近邻查询概念,并给出网络距离受限条件下的模糊图可信近邻查询算法和即时可信近邻查询算法。算法采用模糊模拟方法降低问题难度,使用网络距离约束缩小搜索空间,运用优先队列快速得到满足精度ε要求的可信近邻查询结果。算法的时间复杂度分别为O((2r+Δr)(e+nlgn)+hlgh+lgn)和O(e+(n+1)lgn)。理论分析与实验结果表明,可信近邻查询算法能够从模糊角度解决不确定网络环境下的近邻查询问题。

不确定网络;模糊图;可信距离;可信近邻;模糊模拟;距离约束

1 概述

不确定性数据处理是数据库查询领域的研究热点,目前已取得很多成果,但这些研究多集中在实体数据的不确定性,在现实中覆盖还不够全面。现实中存在实体间关系的不确定性,如路网结点间路径有时关闭,有时开放,多数是根据车流量而变化的介于关闭和开放间的一个不确定量,这时根据结点间最短路径距离得到的最近邻查询结果并不能保证是最有效近邻。这就需要考虑在不确定网络环境下的近邻查询问题。

对于实体数据的不确定性处理,已有很多好的方法,如文献[1]给出SQL查询方法,文献[2]给出一种索引方法,文献[3-4]给出k-近邻查询方法,文献[5]给出一种范围查询分析方法。但这些方法并不能直接用于实体间关系的不确定性处理。

已有文献关注这个问题,其中,文献[6]分析了社会网络环境的不确定性、查询需求并给出处理方法。文献[7]给出了移动网络环境使用k近邻查询解决概率路径问题的方法。文献[8]表明生物网络环境也有这样的查询需求。文献[9]使用随机理论给出了不确定网络环境下近邻查询处理方法。将不确定网络环境建模为概率加权图,实体间关系的不确定性用固定概率值表示,定义了概率加权图中结点间各种距离,并基于这些距离进行近邻查询。这些工作都将实体间关系的不确定性建模为概率性,但现实中实体间关系的不确定性有时还表现为模糊性,如路网结点间的畅通程度。

模糊集理论是处理不确定性问题的有力工具,已被广泛用于数据类型[10]和运算定义[11]以及空间查询[12]等领域。本文将探讨使用模糊集理论来处理不确定网络环境下的近邻查询问题。

2 相关概念

模糊集理论在许多实际领域已得到应用。为了度量模糊事件,文献[13]提出了可能性测度,文献[14]提出了必要性测度,之后文献[15]提出了可信性测度。可信性测度被认为是与概率论中的概率测度平行的概念。

定义1(模糊网络) 模糊网络是指在模糊集理论框架下讨论的不确定网络,即网络实体确定而实体间关系的不确定表现为实体间关系的模糊性。

将模糊网络建模为图,网络实体表示为图中结点,实体间关系表示为图中边,实体间关系是模糊的,则得到模糊图,图中边给出可信值,表示边存在的可信度,即实体间关系的可信度。模糊图与普通图类似,可分为有向图与无向图,加权图与无权图。这里讨论的是无向加权模糊图。下面给出模糊图的形式定义。

定义2(模糊图) 设=(V,E,W,Cr)表示模糊图,其中,V表示图的结点集;E表示图的边集;W表示边的权重集;Cr表示边存在的可信度集。w(e)表示边e的权重,cr(e)表示边e存在的可信度。cr(e)＞0,当且仅当e∈E。

图1为模糊图示例。

图1 模糊图示例

设模糊图=(V,E,W,Cr),其中,V={v1,v2,v3,v4},E={v1v2,v1v3,v1v4,v2v3,v2v4},W={w(v1v2),w(v1v3),w(v1v4),w(v2v3),w(v2v4)},Cr={cr(v1v2),cr(v1v3),cr(v1v4),cr(v2v3),cr(v2v4)}。

定义3(样本图) 已知模糊图=(V,E,W,Cr),样本图G是模糊图的一个实例,EG为G的边集,则其可信度cr(G)=

图2是图1所示模糊图的样本图示例,其中,图2(a)为样本图G1,EG1={v1v2,v1v4,v2v3},G1的可信度为cr(G)=cr(v1v2)×cr(v1v4)×cr(v2v3)=0.3×0.7×0.6=0.125。

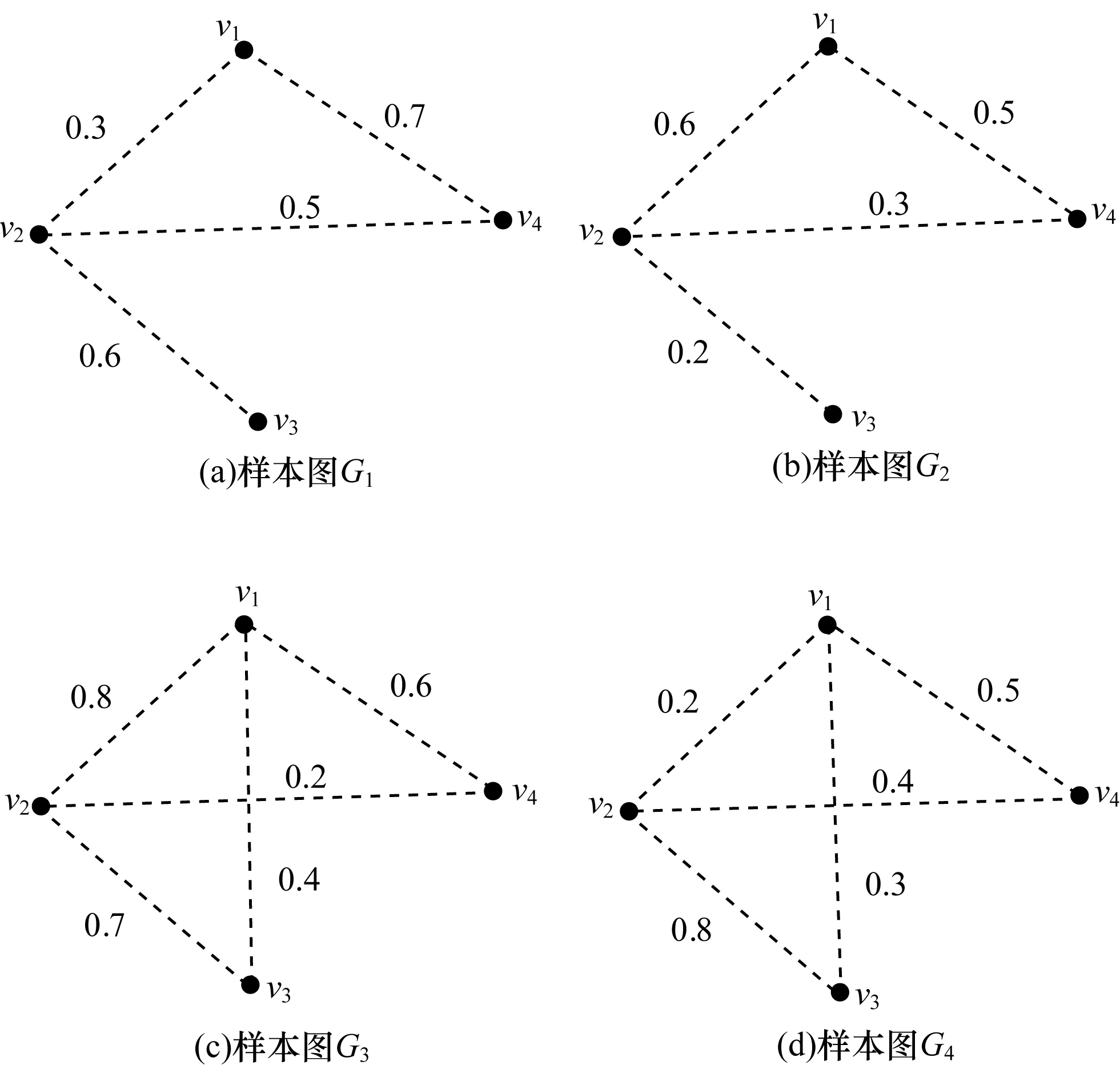
图2 样本图示例

设模糊图=(V,E,W,Cr),G是的样本图,vi,vj∈V,将图中两点间的最小权重表达为两点间的最短路径距离。

定义4样本图中两点间最短路径距离:dG(vi,vj)=d表示vi,vj在G中最短路径距离为d,Ed为G中vi,vj间最短路径边集,dG(vi,vj)为d的可信度cr(dG(vi,vj)=d)=

在图2(a)所示样本图G1中,设v1,v2和v2,v3间距离均为1,则v1,v3间最短路径距离dG1(v1,v3)=2,其边集E2={v1v2,v2v3},dG1(v1,v3)=2的可信度为:

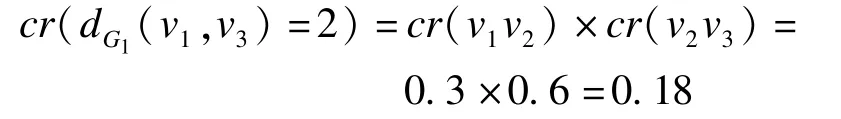
在图2(b)所示样本图G2中,设v1,v2和v2,v3间距离均为1,则v1,v3间最短路径距离dG2(v1,v3)=2,其边集E2={v1v2,v2v3},dG2(v1,v3)=2的可信度为:

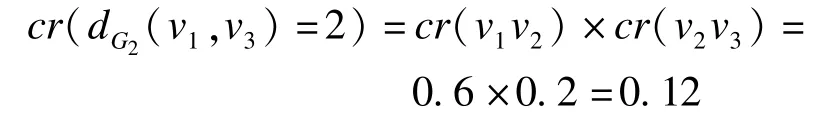
在图2(c)所示样本图G3中,设v1和v3间距离为1,则v1,v3间最短路径距离dG3(v1,v3)=1,其边集E1={v1v3},dG3(v1,v3)=1的可信度为:

在图2(d)所示样本图G4中,设v1和v3间距离为1,则v1,v3间最短路径距离dG(v1,v3)=1,其边集E1={v1v3},dG4(v1,v3)=1的可信度为:

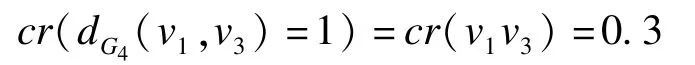
定义5模糊图中两点间最短路径距离:模糊图中vi,vj间最短路径距离记为d(vi,vj),d(vi,vj)为d的可信度为:

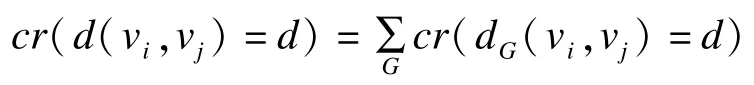
设图2所示为模糊图的所有样本图,其中满足v1,v3间最短路径距离dG(v1,v3)=2的样本图为图2(a)、图2(b),则模糊图中v1,v3间最短路径距离d(v1,v3)=2的可信度为:

满足v1,v3间最短路径距离dG(v1,v3)=1的样本图为(c)(d),则模糊图中v1,v3间最短路径距离d(v1,v3)=1的可信度为:

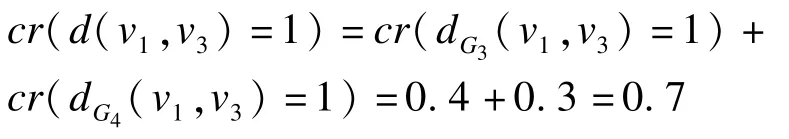
定义6可信最短路径距离:vi,vj间可信最短路径距离

根据上述假设与计算可知,图1所示模糊图中v1,v3间可信最短路径距离为:

定义7可信最短路径期望距离:vi,vj间可信最短路径期望距离

在图1所示模糊图中,v1,v3间最短路径期望距离为:

3 模糊图的存储方法

模糊图=(V,E,W,Cr)中的V,E,W相对稳定,而Cr则变化较大,因此在存储时分开存储,用指针相连。使用邻接表对模糊图进行表示。模糊图=(V,E,W,Cr)的邻接表表示由一个包含|V|个列表的数组所组成,其中每个列表对应于V中的一个顶点。对于每一个vi∈V,邻接表li包含所有满足条件vivj∈V的结点vj。邻接表形式为li:＜vj,w(vivj),pt1,pt2,next＞。其中,li表示结点vi的邻接表;vj表示vi的邻接点;w(vivj)表示vivj的权重,在图中简记为wij;pt1为指向vivj具体抽象数据类型所在页指针,而抽象数据类型的前后分别设置指针指向结点邻接表所在页;pt2为指向邻接表中动态部分存储位置的指针,其存储格式为三元数组,数组第一个位置表示样本图号,数组第2个位置表示vj和vi在样本图中是否邻接的逻辑值,若在样本图中两结点邻接,则逻辑值为1,否则逻辑值为0,数组第3个位置表示vivj在样本图中的可信度。next[vj]为指向vj的后继元素指针,若next[vj]指向null,则vj没有后继元素,它是尾。

图1、图2所示的模糊图的样本图的表示形式如图3所示。

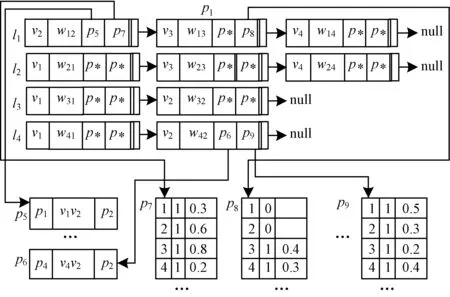
图3 模糊图的表示形式

以结点v1为例。v1有3个邻接点v2,v3和v4,则其邻接表l1包括形式相同的3项。以第一项为例,其形式为＜v2,w12,p5,p7,next＞,其中,v2是v1的邻接点;w12表示v1v2的权重;p5为边v1v2的具体抽象数据类型所在页,而v1v2的具体抽象数据类型的前后的p1和p2分别为结点v1和v2的邻接表所在页;p7为边v1v2的动态信息所在页,next[v2]指向后继元素v3。p7中第一行＜1,1,0.3＞为样本图G1中v1v2的动态信息,第一位置的1表示样本图为G1,第二位置的1表示在样本图G1中v1v2连接,第三位置的0.3表示在样本图G1中v1v2连接的可信度,其他行同理,分别表示样本图G2,G3和G4中v1v2的动态信息。

给定一个新的结点vk,不妨设其邻接点为vi…vj,过程Adjacent-insert将vk加入到邻接表中。

Adjacent-insert(L,vk):

(1)建立vk邻接表lk,包含项＜vi,wki,p∗,p∗,next＞…＜vj,wkj,p∗,p∗,next＞;

(2)对邻接表li…li,增加项 ＜vk,wk∗,p∗,p∗,next＞,原尾部指针指向新加项,而next[vk]指向null;

给定一个已有结点vk,不妨设其邻接点为vi…vj,过程Adjacent-delete将从邻接表中删除vk。

Adjacent-delete(L,vk):

(1)删除vk邻接表lk;

(2)在邻接表li…li中,若项＜vk,wk∗,p∗,p∗,next＞位于邻接表头部,则直接删除;若其位于邻接表中部,则将其前序结点的next指针指向其后继结点,删除此项;若其位于邻接表尾部,则将其前序结点的next指针指向null,删除此项。

4 可信距离计算

模糊图中可信距离的精确计算代价较高,需在所有可能样本图中计算点间的最短路径距离和点间路径存在的可信度,复杂度达到指数级。这里使用对模糊系统进行抽样实验的模糊模拟技术进行近似计算。模糊模拟技术没有随机模拟技术成熟,没有大数定理来保证抽样结果的精确度,但可将模糊理论与模糊模拟结合使用来得到满意的近似值。

定义8设ξ1,ξ2,…,ξr是独立同分布的模糊变量,有相同有限期望值。若ε}=0,则称模糊变量序列{ξi}依可信性收敛到 ξ[16]。

定义9设ξ1,ξ2,…,ξr是独立同分布的模糊变量,有相同有限期望值。若,则称模糊变量序列{ξi}依均值收敛到ξ[16]。

4.1 可信最短路径距离计算

根据定义8可通过过程Compute-dC(q,v)得到可信最短路径距离的近似值。

Compute-dC(q,v):

(1)在模糊图中均匀抽取r个样本,计算每个样本图中vi,vj两点间最短路径距离d及其可信度,得到模糊图中vi,vj两点间最短路径距离为d的近似可信度:

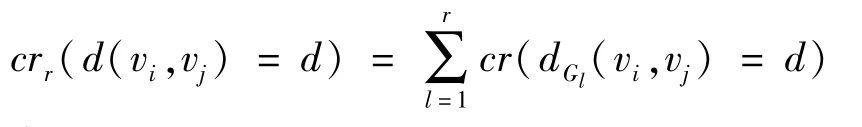
(2)在模糊图中均匀抽取r+Δr个样本,计算每个样本图中vi,vj两点间最短路径距离d及其可信度,得到模糊图中vi,vj两点间最短路径距离为d的近似可信度:

(3)若对精度ε＞0

|crr+Δr(d(vi,vj)=d)-crr(d(vi,vj)=d)|≤ε

则crr+Δr(d(vi,vj)=d)即作为模糊图中vi,vj两点间最短路径距离为d的近似可信度。否则令r=r+Δr,转(2)。

(4)比较vi,vj两点间最短路径距离的近似可信度,其中使近似可信度最大的d值即为vi,vj两点间可信最短路径距离dC(q,v)的近似值。

定理1设模糊图中两点间最短路径距离的可信度是收敛的,则对任意ε＞0,当r→∞时,有:

在模糊模拟理论中,因模糊变量收敛,所以模拟结果应与其极限值接近,但其极限值无法实际得到,因此使用两次模拟结果的差值来作为模拟结束的条件。

根据定理1和模糊模拟理论可知,若对任意ε＞0,|crr+Δr(d(vi,vj)=d)-crr(d(vi,vj)=d)|≤ε,则crr+Δr(d(vi,vj)=d)即可作为模糊图中vi,vj两点间最短路径距离为d的精度为ε的近似可信度。

假设模糊图的基图结点数为n,边数为e。抽取r个样本,每个样本图中,vi,vj两点间最短路径距离的计算使用 Dijkstra算法,时间复杂度为O(e+nlgn),计算模糊图中vi,vj两点间最短路径距离为d的近似可信度的时间复杂度为r,即第一步的时间复杂度为O(r(e+nlgn)),第2步同理,时间复杂度为O((r+Δr)(e+nlgn)),第3步时间复杂度为常数,第4步若设vi,vj两点间最短路径距离的可能值有h个,则其时间复杂度O(hlgh)),即可信最短路径距离计算的时间复杂度为O((2r+Δr)(e+nlgn)+hlgh)。

4.2 可信最短路径期望距离计算

根据定义9可通过过程Compute-dCE(q,v)得到可信最短路径期望距离的近似值。过程 ComputedCE(q,v)与Compute-dC(q,v)类似。

定理2设模糊图中两点间可信最短路径期望距离是收敛的,则对ε＞0,当r→∞时,有:

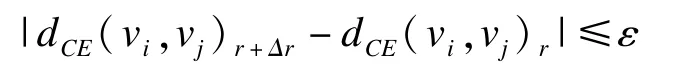
定理2的证明与定理1的证明类似。同理,若对任意ε＞0,有|dCE(vi,vj)r+Δr-dCE(vi,vj)r|≤ε,则dCE(vi,vj)r+Δr即可作为模糊图中vi,vj两点间可信最短路径期望距离的精度为ε的近似值。

可信最短路径期望距离计算的时间复杂度也为O((2r+Δr)(e+nlgn)+hlgh)。这个关于结点数和边数的多项式近似解法比精确指数解法可行,且精度可以根据需要调节。

5 可信近邻查询

定义10可信k近邻查询:已知模糊图=(V,E,W,Cr),查询对象q∈V,可信k近邻查询给出与q的可信最短路径距离(或可信最短路径期望距离)最小的V中k个对象,即对∀v∈V,有:

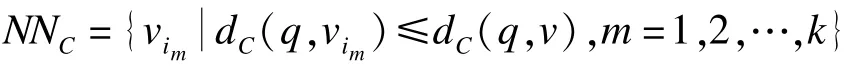
近邻查询是要找到与查询对象距离较近的目标对象,若结果与查询对象距离较远,则失去意义,因此这里仅考虑距离受限的近邻查询,从而缩小搜索空间。

算法思想:算法中设置了一结点集NNC,从查询点q到NNC中结点的可信最短路径距离均已确定。算法反复计算访问结点v与查询点q的可信最短路径距离,若小于NNC中结点的可信最短路径距离,则将v加入NNC中。

以可信最短路径距离为基础的可信k近邻查询算法描述如算法1所示。

算法1可信k近邻查询算法

输入模糊图=(V,E,W,Cr),查询点q∈V,样本数初值r,样本数增量Δr,近邻数k,距离约束D,精度ε

输出k-NN查询结果集NNC

定理3模糊图=(V,E,W,Cr),查询点q∈V。对该图运行可信k近邻查询算法,则在算法终止时,对在距离约束D范围内的所有v∈V,有:

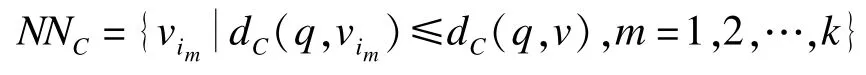
证明:初始化:初始时,NNC为空集,显然成立。

保持:dC-max为NNC中结点与q的最大可信最短路径距离,当NNC为空集时,dC-max为无穷大。NNC中元素个数未达到k个时,则将v直接加入NNC,否则比较v与q的dC(q,v)和dC-max。若小于dC-max,则放入NNC,大于dC-max,则舍去。这就使NNC中结点是当前已访问结点中与查询点q可信最短路径距离最小的k个结点。

终止:在终止时,所有与q的距离小于预先给定距离D的结点,均已访问,且与dC-max比较完毕。因此,对在距离约束D范围内的所有v∈V,有:

算法分析:算法1中的步骤(4)～步骤(6)是每个访问结点与查询点p的可信最短路径距离及其可信度的计算过程,其复杂度为O((2r+Δr)(e+nlgn)+hlgh),步骤(7)～步骤(9)是利用优先队列找到k个近邻,其时间复杂度最坏为O(lg(n)),即算法1的时间复杂度为O((2r+Δr)(e+nlgn)+hlgh+lgn)。

以可信最短路径期望距离为基础的近邻查询算法,这里称为算法2(略),与算法1过程相同,只是步骤(6)中可信最短路径期望距离及其可信度的计算与算法1不同,其正确性证明与时间复杂度也与算法1相同。

在现实应用中,还有即时可信近邻的查询需求,这种需求想知道某时的可信近邻情况,而不想知道模糊网络的整体情况,针对这种需求,给出算法3。

算法2即时可信近邻查询算法

输入模糊图=(V,E,W,Cr),查询点q∈V,近邻数k,距离约束D

输出k-NN查询结果集NNC

算法3的正确性证明与算法1同理。算法3中步骤(3)～步骤(5)是计算每个访问结点与查询点的距离及其可信度,其时间复杂度为O(e+nlgn),步骤(6)、步骤(7)行是访问结点与当前近邻对象可信度的比较,其时间复杂度为O(lg(n)),即算法3的时间复杂度为O(e+(n+1)lgn)。

6 实验结果分析

实验在 2.0 GHz双核处理器、1 GB内存、Windows XP平台上用Visual C++6.0实现。实验数据使用2个路网,一个是人工合成网N1,使用模拟器产生100 000个平面点,随机连接点形成边,对边在[1,10]区间范围内赋权重,对边在[0,1]区间范围内赋可信度,点的最大出度设为10。另一个是实际路网N2,从Digital Chart of World(DCW)获得,包含430 274个结点、594 104条边。将边的可信度设为边的通过时间的倒数。使用本文所述的存储结构对两个网络进行存储,页面大小为4K。

实验分为2个部分,第1部分测试可信距离的特征,第2部分测试各个参数对基于可信距离的近邻查询算法的影响。

实验1测试可信距离的分布情况。为估计可信距离分布,在2个实验数据网中分别抽取300个样本,每个样本中遍历300个结点累积距离,距离的分布结果如图4所示。从图4可知,2个实验网络情况相似,2个距离函数有相似分布,且与确定图中最短路径距离函数的分布相似。

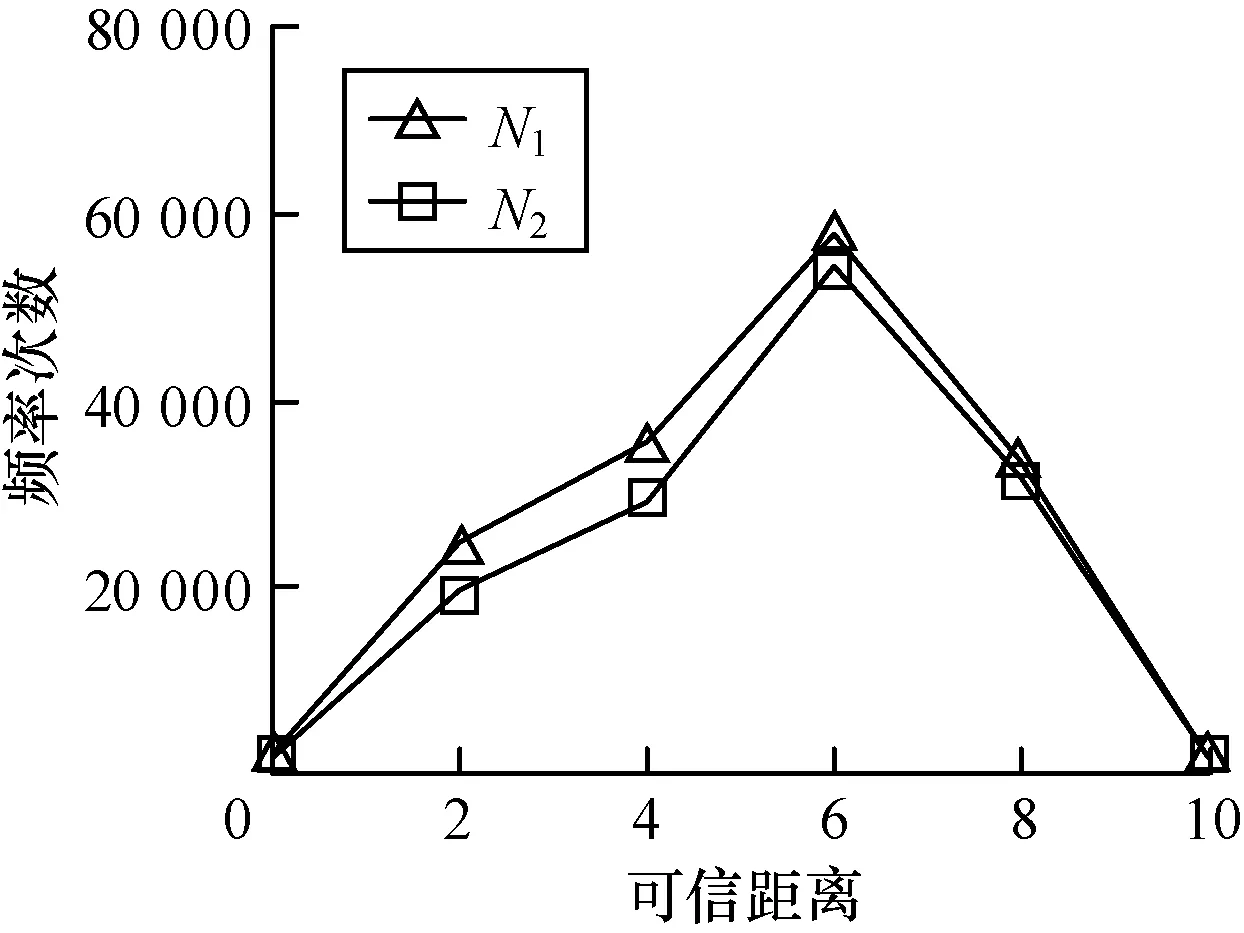
图4 可信距离分布

实验2测试可信距离的收敛性与样本数的关系。在2个网络中分别以300个样本的结果为基准,计算不同样本数时近似距离的均方差。结果如图5所示,从图5可知随着样本数的增加,均方差趋于0,可信距离依样本数收敛。

图5 可信距离与样本数关系

实验3测试k值与基于可信距离的近邻查询算法性能的关系。因可能成为近邻查询结果的是近邻查询过程中Dijkstra算法访问的结点,故以访问结点数与图的总结点数的比值为主要衡量标准,来评估近邻算法的的性能。图6是样本数为200时,访问结点数与k值的关系结果图,从图6可知随着k值增加,访问结点数缓慢增加,近邻查询算法的性能随之下降。

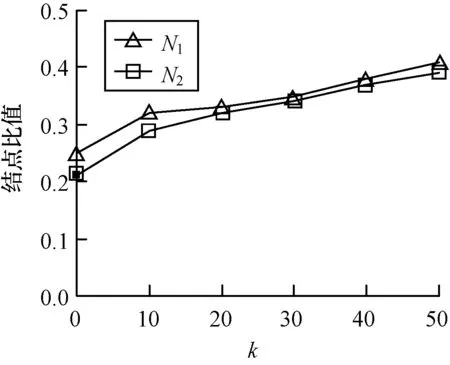
图6 k值与算法性能关系

实验4测试样本数与基于可信距离的近邻查询算法性能的关系。图7是k=20时,访问结点数与样本数的关系结果,从图7可知随着样本数增加,访问结点数初期也急剧增加,但样本数达到一定数值后,访问结点数渐趋平稳,没有出现性能极剧恶化的情况。

图7 样本数与基于可信距离的近邻查询算法性能关系

距离约束D和精度ε分别影响访问结点数和样本数,从而间接影响算法性能。随着距离约束D的增大和精度ε的提高,算法性能下降。

7 结束语

针对不确定网络空间近邻查询问题,将不确定网络建模为模糊图,给出模糊图中可信最短路径距离与可信最短路径期望距离定义,以可信距离为度量,提出可信近邻查询概念,并给出距离受限条件下的可信近邻查询算法和即时可信近邻查询算法。算法使用取样方法进行近似计算,使时间复杂度为指数级的问题在多项式时间内解决,并可根据实际需要进行精度调节。理论分析与实验结果表明算法可行且性能稳定。下一步的研究是同时考虑不确定网络的随机性与模糊性,提高不确定网络的描述能力,使不确定网络环境下的近邻查询更有效。

[1] Cheng R,Kalashniko V D V,Prabhakar S.Querying Imprecise Data in Moving Object Environments[J]. IEEE Transactions on Knowledge and Data Engineering, 2004,16(9):1112-1127.

[2] 庄 毅.ISU-Tree:一种支持概率k近邻查询的不确定高维索引[J].计算机学报,2010,33(10):1934-1941.

[3] Yi Ke,Li Feiei,Kollios G,et al.Efficient Processing of Top-k Queries in Uncertain Databases with X-relations[J]. IEEE Transactions on Knowledge and Data Engineering, 2008,20(12):1669-1682.

[4] 高 峻,郝忠孝.受限网络移动对象的概率最近邻查询[J].计算机工程,2013,39(7):26-30.

[5] 陈逸菲,秦小麟.NU2RA:一种路网中不确定移动对象范围查询分析方法[J].计算机研究与发展,2010, 47(6):1060-106.

[6] Adar E,Re C.Managing Uncertainty in Social Networks[J]. IEEE Data Engineering Bulletin,2007,30(2):15-22.

[7] Ghosh J,Ngo H,Yoon S,et al.On a Routing Problem Within ProbabilisticGraphsand ItsApplication to Intermittently Connected Networks[C]//Proceedings of INFOCOM’07.[S.1.]:IEEE Press,2007:216-222.

[8] Asthana S,King O D,Gibbons F D,et al.Predicting Protein Complex Membership Using Probabilistic Network Reliability[J].Genome Research,2004,14(1): 1170-1175.

[9] Potamias M,Bonchi F,Gionis A,et al.Nearest-neighbor Queries in Probabilistic Graphs[EB/OL].[2009-10-21]. http://www.cs.bu.edu.

[10] Schneider M. Fuzzy Topological Predicates, their Properties,and their Integration into Query Languages[C]//Proceedins of the 9th ACM International Symposium on Advances in Geographic Information Systems.New York,USA:[s.n.],2001:212-221.

[11] Tang X,Kainz W.Analysis of Topological Relations between Fuzzy Regions in a General Fuzzy Topological Space[C]//Proceedings of Canadian Geomatics Conference.Ottawa,Canada:[s.n.],2002:114-129.

[12] Zheng Kai,Fung Pui Cheong,Zhou Xiaofang.K-Nearest Neighbor Search for Fuzzy Objects[C]//Proceedings of 2010 ACM SIGMOD International Conference on Management of Data.Indiana,USA:IEEE Press,2010: 333-345.

[13] Zadeh L A.Fuzzy Sets as a Basis for a Theory of Possibility[J].Fuzzy Sets and Systems,1978,(1): 3-28.

[14] Zadeh L A.Mathematical Frontiers of the Social and Policy Sciences[M].Boulder,USA:Westview Press,1979.

[15] Liu Baoding,Liu Yankui.Expected Value of Fuzzy Variable and Fuzzy Expected Value Models[J].IEEE Transactions on Fuzzy Systems,2002,10(4):445-450.

[16] Liu B.Uncertainty Theory:An Introduction to Its Axiomatic Foundations[M].Berlin,Germany:Springer-Verlag,2004.

编辑 索书志

Credible Nearest Neighbor Query in Constraint Fuzzy Network

GAO Jun1,HAO Zhongxiao1,2
(1.College of Computer Science and Technology,Harbin University of Science and Technology,Harbin 150080,China; 2.College of Computer Science and Technology,Harbin Institute of Technology,Harbin 150001,China)

This paper gives a new method for solving the problem of the nearest neighbor query in uncertain network.The method is that,gives the definition of credible shortest path distance and credible shortest path expectation distance,based on credible distance,puts forward the concept of fuzzy graph credible nearest neighbor query,and proposes fuzzy graph credible nearest neighbor query algorithm and instant credible nearest neighbor query algorithm on the condition of network distance constraint.The algorithm decreases the difficulty of the problem by using fuzzy analog,diminishes search space by using network distance constraint and quickly acquires the result of credible nearest neighbor query according to the precisionε by using the priority queue.The complexity of the algorithm isO((2r+Δr)(e+nlgn)+hlgh+lgn)andO(e+(n+1)lgn). Theory analysis and experimental results show that fuzzy graph credible nearest neighbor query algorithm can solve the problem of the nearest neighbor query in uncertain network at the angle of fuzzy quality.

uncertain network;fuzzy graph;credible distance;credible nearest neighbor;fuzzy analog;distance constraint

1000-3428(2015)01-0054-07

A

TP311.13

10.3969/j.issn.1000-3428.2015.01.010

黑龙江省自然科学基金资助项目(F200821)。

高 峻(1972-),女,副教授、博士研究生,主研方向:时空数据库技术;郝忠孝,教授、博士生导师。

2013-09-24

2013-12-26 E-mail:hustgj@163.com

中文引用格式:高 峻,郝忠孝.受限模糊网络可信近邻查询[J].计算机工程,2015,41(1):54-60.

英文引用格式:Gao Jun,Hao Zhongxiao.Credible Nearest Neighbor Query in Constraint Fuzzy Network[J].Computer Engineering,2015,41(1):54-60.