基于小波－人工免疫算法的框架结构损伤识别

管德清，陈豫洲，李 冉

（长沙理工大学土木与建筑学院，湖南长沙 410004）

框架是建筑结构中一种较普遍使用的结构形式，会因各种原因不可避免地存在损伤，对结构的安全构成威胁，因而研究框架结构的损伤识别方法具有重要意义。小波是一种具有多分辨率的时频分析方法，其具有空间局部化特性而能较好地分析信号的奇异性位置。近年来，人们开始采用小波理论研究结构的损伤诊断问题［1］。Huang［2］等人以一个3层不对称钢框架结构为研究对象，运用小波分析的方法，对其损伤进行了有效识别。Ovanesova［3］等人以框架结构为研究对象，对结构支座和梁柱接点处的裂缝运用离散小波变换的方法有效地进行了识别。管德清［4－5］等人以含裂缝的平面框架结构为研究对象，建立了基于应变模态小波分析识别结构损伤位置的方法，用数值计算证明了该方法的有效性。唐雪松［6］等人以一在建特大斜拉桥双悬臂施工状态下的结构为分析对象，证明了基于曲率模态的小波变换信号能有效识别出施工中结构的损伤。

人工免疫算法是模仿生物免疫系统的运行机制而建立的一种学习、优化的人工智能算法。生物免疫系统的主要功能就是识别和清除进入生物体的外部有害物质，具有识别“自我”与“非我”的能力［7］。在这一原理的启发下，近年来，人工免疫算法被运用于结构的损伤检测上。孙万泉［8］等人将免疫算法运用于结构动态参数的识别，通过算例，证明了免疫算法能实现对结构动态参数快速而精确的识别，并具有较好的抗噪声能力。周悦［9］等人研究了人工免疫系统的仿生机理，提出了一种基于Diagonal距离的人工免疫模式来解决结构损伤识别和分类的问题，取得了有意义的结果。郭惠勇［10］等人建立了平面二维桁架结构有限元模型，将免疫遗传算法和贝叶斯融合理论相结合，对结构的损伤位置和程度进行了识别，但该方法仍存在损伤位置定位不准确和免疫遗传算法搜索效率不高的缺点。他们的研究表明：小波分析方法能够有效识别结构损伤的位置，但是，对于结构损伤程度的识别效果还很不理想。如果采用人工免疫算法来识别结构损伤的位置，使得识别损伤的单元数比实际损伤的单元数要多，种群规模就会相应增大，导致搜索空间较大，搜索效率较低。当结构复杂时，可能造成无法完成计算的后果。作者研究发现，在确定了结构的损伤位置后，经过一定的处理，就可以利用人工免疫算法，较准确地识别损伤程度。作者在以往研究结果的基础上，拟建立一种能够识别结构损伤位置和损伤程度的二阶段结构损伤识别新方法：小波－人工免疫算法。用小波分析，确定结构损伤单元的位置。根据小波分析确定的损伤单元位置和数量，设置相应的人工免疫算法种群规模。在有效减小搜索空间的情况下，再来识别结构损伤程度，以期减小人工免疫算法的盲目性，提高效率和精度。并试图用该方法成功识别一平面框架结构的损伤。

1 小波－人工免疫算法的结构损伤识别原理

1.1 基于小波变换的损伤位置识别

小波变换的定义是把某一被称为基本小波的函数ψ（t）作位移τ后，再在不同尺度e下与待分析的信号x（t）做内积。

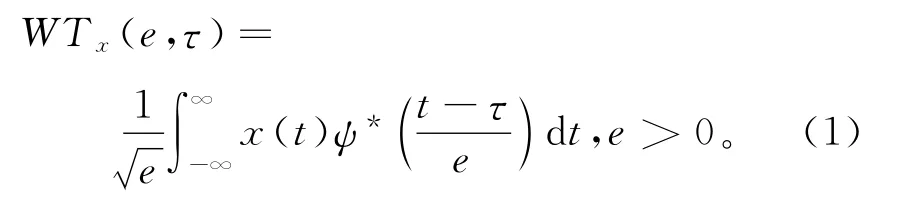
式中：e为尺度因子，反映信号频率信息；τ为平移因子，反映信号时间信息；e，τ，t∈R，且e≠0；ψ＊（t）表示ψ（t）的复共轭。

随着e，τ的变换，使得小波变换具有多分辨的特点。

结构的损伤可归结为结构在某个截面刚度的降低，即抗弯刚度EI降低。在刚度变化截面v的左、右两侧有EI（v＋）≠EI（v－），但结构仍应满足变形协调条件和内力平衡条件。

竖向位移：

转角：

弯矩：

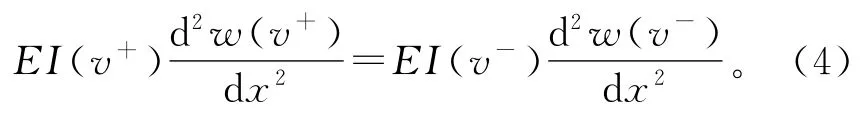
剪力：

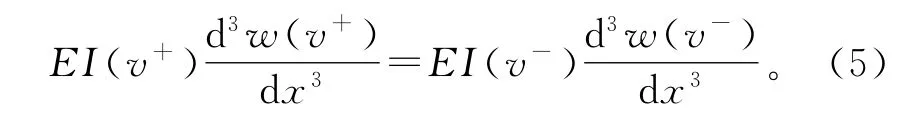
应变和转角的关系为：

式中：x为长度方向的坐标；θ为转角；K为常量。

因为EI（v＋）≠EI（v－），由式（4）可知，则损伤结构的转角振型曲线在裂缝截面一阶导数不连续，即应变模态曲线不连续。因此，可由应变模态来识别结构的损伤。

1.2 基于人工免疫算法的结构损伤定量识别

利用人工免疫算法优越的全局搜索能力来进行结构损伤程度的识别。由于目前人工免疫算法在结构损伤识别方面没有现成的程序工具箱，故本研究使用Matlab语言自主编制程序，流程图如图1所示。

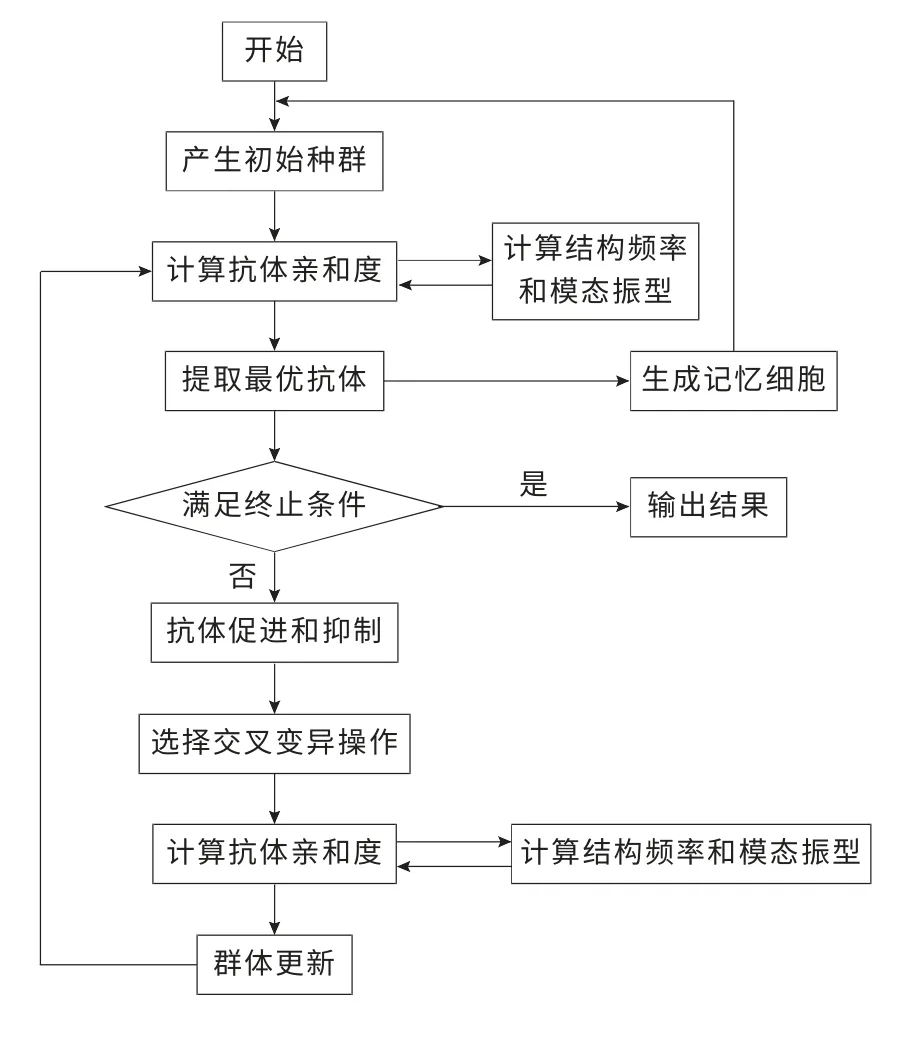
图1 人工免疫算法结构损伤程度识别流程Fig.1 The flow chart of the damage detection by immune algorithm

1.2.1 抗体编码

采用二进制编码来定义损伤单元的损伤程度，本研究的损伤指的是损伤程度小于50%的小损伤，故采用6位的二进制串子体来表示损伤程度。假设小波分析识别出的结构损伤单元个数为q，一个6位的二进制串子体表示一个损伤单元的损伤程度，则q个损伤单元的损伤程度就用q个子体来表示，如：A1＝011001，A2＝100101，…，Aq＝001010。其中每个子体中二进制串的值定义为百分比值，例如：001010表示10%。当其中一个子体的值大于50%时，因这里的损伤指的是小损伤，故重新定义其值为50%。将这q个子体合成为一个抗体，便可以表示q个损伤单元的损伤程度，即：抗体

1.2.2 目标函数的建立

基于结构的频率和模态振型，以频率误差函数和模态振型误差函数的加权和最小为目标，采用的目标函数为：

式中：Fω和Fφ均为加权因子和分别为第a阶实测和计算的固有频率和分别为第a阶经过归一化处理后的实测和计算的振型；m为频率阶数；n为振型阶数；k为节点位移数目。

该目标函数是最小化问题，要求搜索得到的解使目标函数最小。该目标函数因含有频率和位移模态振型2种不同数据，故能较好地应用于结构损伤识别。

1.2.3 抗体适应度

式中：（Ag）z为抗原Ag与抗体z之间的亲和度，其值在0和1之间，它越大，表示亲和度越高；tz为抗原Ag与抗体z之间的结合强度，tz≥0，其值由式（7）计算得到。

1.2.4 抗体相似度

免疫系统是由抗体组成的不确定系统，可采用Shannom信息熵来表示其多样性。假设免疫系统由N个抗体组成（种群规模为N），每个抗体有M个基因，第j个基因的信息熵为：

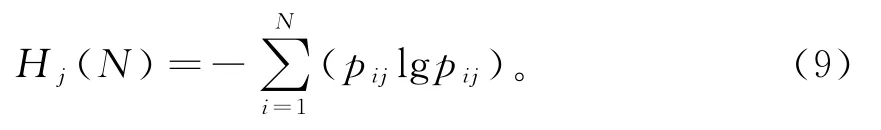
式中：pij为在基因座j上产生等位基因i的概率。则系统多样性的平均信息熵为：

于是，抗体u和z之间的相似度为：

式中：H（2）为抗体u和z的平均信息熵，由（10）式得到。

1.2.5 抗体浓度

抗体浓度过高表示群体多样性差，最终可能导致得不到全局最优解。抗体浓度为：

式中：Auz为由式（11）计算得到的抗体u与z之间的相似度；λ为相似度常数，取值范围为0.9～1.0。

1.2.6 抗体促进与抑制及选择交叉变异操作

对亲和度较高的抗体进行促进的同时，对抗体浓度较大的抗体进行抑制。这样，既加快了收敛速度又保证了抗体的多样性，且避免出现过早收敛的情况。在对亲和度较高的抗体进行保留的同时，对亲和度不高的抗体采用选择交叉、变异的方式，产生新的抗体，进行群体的更新。本研究采用单点交叉，交叉概率取0.9；按照概率对基因进行变异，变异概率为0.1。

1.2.7 迭代终止条件

同时使用了3条准则，满足其中一条则认为找到了最优解，人工免疫算法自动停止：①选择一个适当的数y（本研究选择y＝50），当迭代计算时群首抗体连续y次不变，则认为找到最优解。②最优抗体的目标函数J小于某个很小的值（本研究取10－8），则意味着找到最优解。③迭代的最大次数达到某个值（本研究取300次），则计算结束。

2 数值模拟分析

以含损伤的一层一跨平面钢框架结构（如图2所示）为研究对象，该结构模型的跨度和高度均为3 000mm。梁柱采用刚性连接，两柱与地面连接方式简化为固接。梁柱截面采用等截面，截面尺寸为200mm×250mm。材料密度为7 800kg／m3，弹性模量为2.1×1011N／m2，泊松比为0.3。建立结构有限元模型，将整个框架结构划分为300个单元，按A－B－C－D顺序给框架单元标号为1＃～300＃，每个单元中心点间距为30mm。结构的损伤通过降低单元刚度的方法来模拟。本研究假定有2种工况。工况一：30＃单元（距A点900mm）存在损伤，其损伤程度为10%；120＃单元（距B点600mm）存在损伤，其损伤程度为20%。工况二：80＃单元（距A点2 400mm）存在损伤，其损伤程度为15%；130＃单元（距B点900mm）存在损伤，其损伤程度为25%；270＃单元（距C点2 100mm）存在损伤，其损伤程度为30%。

图2 一层一跨框架结构有限元模型示意（单位：mm）Fig.2 Finite element model of 1－bay，1－story frame structure（unit：mm）

2.1 工况一

2.1.1 小波分析识别结构的损伤位置

建立结构的有限元模型，运用Lanczos法计算，得到损伤结构的第一阶应变模态。运用Matlab计算软件，进行小波分析。选取DB2小波，对结构的应变模态进行尺度1连续小波变换，得到小波系数如图3所示。从图3中可以看出，小波图中有2处奇异点（30＃和120＃），突变处正好对应框架结构的损伤单元位置，与假设相符。

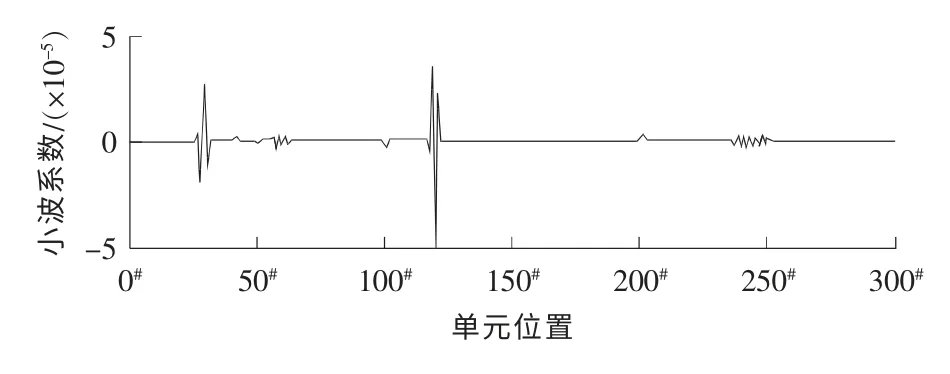
图3 含2处损伤框架结构的小波系数示意Fig.3 Wavelet coefficients of the frame structure with two damages

2.1.2 人工免疫算法识别结构的损伤程度

采用人工免疫算法，进行损伤程度分析。群体数量取100，采用前10阶频率和第一阶振型模态，进行损伤程度识别。因初始种群的产生具有随机性，故本研究采用10次运算后的平均值作为最终的损伤程度定量结果，工况一的10次损伤识别结果见表1。因采用多次运行进行识别，故迭代过程中最优抗体的目标函数变化过程只画出迭代次数最多的一次（第6次），如图4所示。从表1损伤识别结果可以看出，30＃单元的损伤程度为10%，120＃单元的损伤程度为20%，与假设相符。

表1 工况一的10次人工免疫算法损伤识别结果Table 1 Damage detection result of 10artificial immune algorithm operations in Mode 1

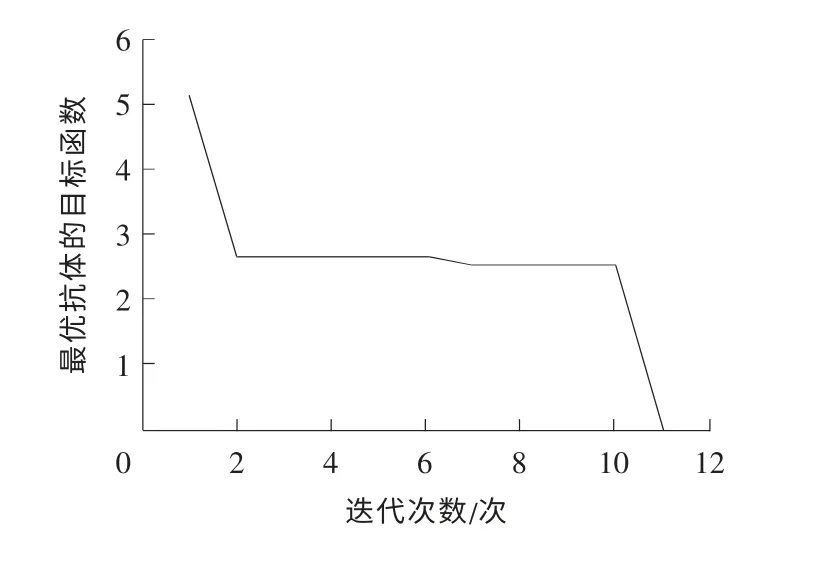
图4 工况一中，最优抗体的目标函数变化过程Fig.4 The objective function value of the optimal antibody change process in Mode 1

2.2 工况二

2.2.1 小波分析识别结构的损伤位置

建立结构的有限元模型，运用Lanczos法计算，得到损伤结构的第一阶应变模态。运用Matlab计算软件，进行小波分析。选取DB2小波，对结构的应变模态进行尺度1连续小波变换，得到小波系数如图5所示，从图5中可以看出，小波图中有3处奇异点（80＃，130＃和270＃），突变处正好对应框架结构的损伤单元位置，与假设相符。

2.2.2 人工免疫算法识别结构的损伤程度

图5 含3处损伤框架结构的小波系数示意Fig.5 Wavelet coefficients of frame structure with three damages

采用人工免疫算法，进行损伤程度分析。群体数量取150，采用前10阶频率和第一阶振型模态，进行损伤程度识别。因初始种群的产生具有随机性，故本研究采用10次运算后的平均值作为最终的损伤程度定量结果，工况二的10次损伤识别结果见表2。因采用多次运行进行识别，故迭代过程中最优抗体的目标函数变化过程只画出迭代次数最多的一次（第5次），如图6所示。从表2中可以看出，80＃单元的损伤程度为15%，130＃单元的损伤程度为25%，270＃单元的损伤程度为30%，与假设相符。

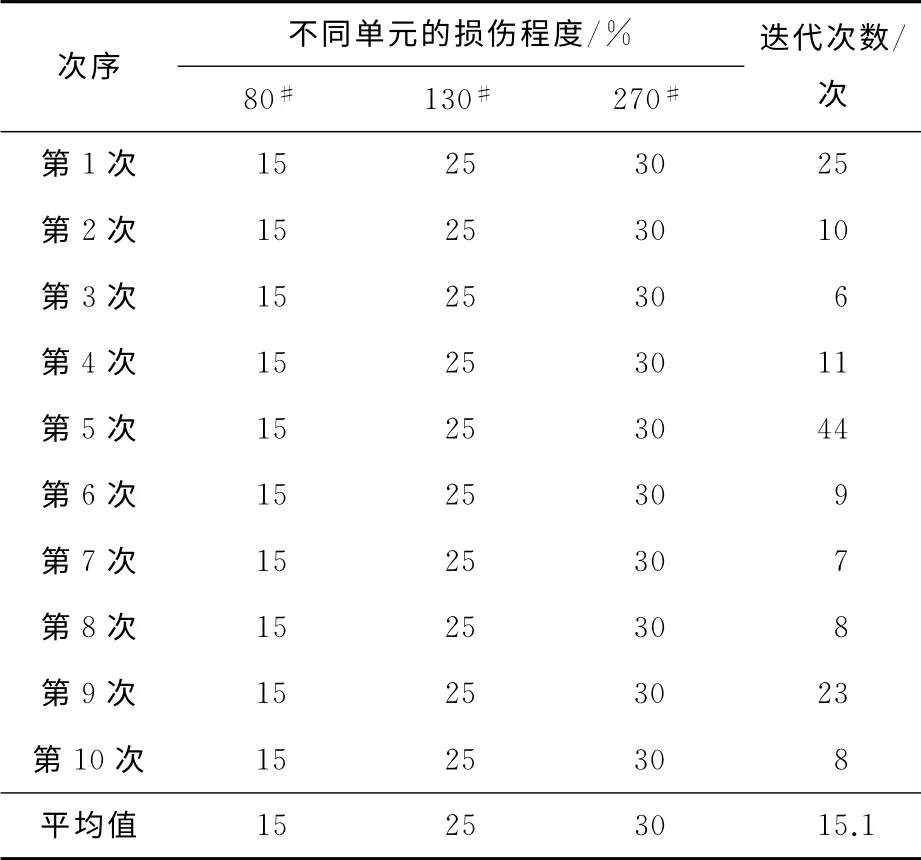
表2 工况二的10次人工免疫算法损伤识别结果Table 2 Damage detection result of 10artificial immune algorithm operations in Mode 2

图6 工况二中，最优抗体的目标函数变化过程Fig.6 The objective function value of the optimal antibody change process in Mode 2

2.3 结果分析

从计算结果可以发现，小波分析能有效识别结构的损伤位置，人工免疫算法能较精确地识别结构的损伤程度。将2种方法相结合的小波－人工免疫算法综合了两者的优点，且补充了相互的不足。在用小波分析方法确定了结构损伤单元的位置以后，人工免疫算法在进行迭代计算时只需较少的迭代次数便可计算出最优解。该方法提高了计算效率，降低了对电脑硬件的要求。这对于复杂结构的计算有重要意义。

3 结论

1）运用小波分析和人工免疫算法相结合，提出了小波－人工免疫算法的概念，建立了一种有效识别结构损伤位置和程度的新方法。

2）用有限元计算分析，得到了结构的应变模态。对模态参数进行连续小波变换，得到了小波系数图。由小波系数图中的奇异点位置来判断结构损伤的位置。在得到结构损伤位置的基础上，再利用人工免疫算法识别结构损伤程度的数值计算，验证了该方法的有效性。

3）用小波分析方法，确定了结构的损伤单元位置。再根据小波分析，确定损伤单元的数量，设置人工免疫算法相应的种群规模。在有效减小搜索空间的情况下，识别结构的损伤程度可以减少算法的盲目性，提高计算效率和精度。

4）本研究所建立的小波－人工免疫算法可使搜索空间大大减小，提高了搜索效率，可为复杂工程结构损伤位置和损伤程度的识别提供参考。

（References）：

［1］Wang Quan，Deng Xiaomin.Damage detection with spatial wavelets［J］.International Journal of Solids and Structures，1999，36：3443－3468.

［2］Huang C S，Su W C.Identification of modal parameters of a time invariant linear system by continuous wavelet transformation［J］.Mechanical Systems and Signal Processing，2007，21（4）：1642－1664.

［3］Ovanesova A V，Suarez L E.Applications of wavelet transforms to damage detection in frame structures［J］.Engineering Structures，2004，26（1）：39－49.

［4］Guan Deqing，Zhong Xiaolin，Ying Hongwei.Research on sheet crack identification of frame structure using wavelet analysis［J］.Applied Mechanics and Materials，2011，71－78：4074－4077.

［5］管德清，黄燕.基于应变模态小波变换的框架结构损伤识别研究［J］.计算力学学报，2010，27（2）：325－341.（GUAN De－qing，HUANG Yan.Damage identification of the frame structure by means of wavelet analysis of strain mode［J］.Chinese Journal of Computational Mechanics，2010，27（2）：325－341.（in Chinese））

［6］唐雪松，谭珂，陈星烨.斜拉桥结构施工状态下连续小波变换损伤识别方法［J］.长沙理工大学学报：自然科学版，2010，7（1）：31－38.（TANG Xue－song，TAN Ke，CHEN Xing－ye.Damage identification based on continuous wavelet transformation for a real cablestayed bridge structure under the construction condition［J］.Journal of Changsha University of Science and Technology：Natural Science，2010，7（1）：31－38.（in Chinese））

［7］Ahammed M，Melchers R E.Gradient and parameter sensitivity estimation for systems evaluated using Monte Carlo analysis［J］.Reliability Engineering and System Safety，2006，91（5）：594－601.

［8］孙万泉，马震岳.基于一种免疫算法的结构动态参数识别［J］.计算力学学报，2005，22（2）：155－159.（SUN Wan－quan，MA Zhen－yue.Identification of the structure dynamic parameter based on an immune algorithm［J］.Chinese Journal of Computational Mechanics，2005，22（2）：155－159.（in Chinese））

［9］周悦，唐世，贾雪松，等.基于人工免疫模式识别的结构损伤检测与分类算法［J］.沈阳建筑大学学报：自然科学版，2013，29（2）：378－384.（ZHOU Yue，TANG Shi，JIA Xue－song，et al.Structural damage detection and classification algorithm based on artificial immune pattern recognition［J］.Journal of Shenyang Jianzhu University：Natural Science，2013，29（2）：378－384.（in Chinese））

［10］郭惠勇，李正良.免疫遗传算法在结构损伤识别中的应用与改进［J］.土木建筑与环境工程，2012，34（2）：7－26.（GUO Hui－yong，LI Zheng－liang.Improvement and application of immune genetic algorithm in structural damage identification［J］.Journal of Civil，Architectural ＆Environmental Engineering，2012，34（2）：7－26.（in Chinese））