极化分集下的共形阵列波达方向估计
刘 超 丁志中
极化分集下的共形阵列波达方向估计
刘 超 丁志中
(合肥工业大学,安徽合肥230009)
提出了一种基于双馈源共形阵列的极化分集信号盲极化波达方向(Direction of Arrival,DOA)估计方法.通过投影和旋转变换,分析并给出了双馈源共形阵列下正交极化分集信号的等效导向矢量,将信号空间划分为两个正交极化信号子空间,实现了正交极化信号的盲极化分离.在此基础上给出了基于多重信号分类(Multiple Signal Classification,MUSIC)的极化信号的DOA估计算法.该算法无需估计极化参数,能够实现任意共形阵列对正交极化分集信号的DOA估计,最大估计信号数目能够超过阵元个数.仿真实验验证了该算法具有很好的估计性能.
共形阵列;极化分集;波达方向估计;多重信号分类算法
引 言
由于共形阵列能够安装在载体的曲面表面,具有节约空间、减少雷达散射截面、增大角度覆盖区域等诸多优点.对于战斗机、无人飞机、巡航导弹等体积较小、机动性强的飞行平台,共形阵列能够在保证原有的作战机动性的同时实现较高的天线增益,灵活的大范围角度扫描,较强的干扰抑制能力,在雷达、无线通信、航空航天等领域都具有十分广阔的应用前景[1].波达方向(Direction of Arrival,DOA)估计作为电子侦查对抗、无线通信的一项重要技术,已受到广泛关注.然而由于共形阵列复杂的曲面结构,各个天线单元方向图的不一致性使得共形阵列无法再被看作简单的各向同性阵列来处理,许多适用于经典阵列的DOA估计方法在共形阵列天线中无法简单移植应用.目前已经有许多学者对该领域展开研究,并取得了一定成果.文献[2]给出了一种基于矩阵束的DOA估计算法.文献[3]将多重信号分类(Multiple Signal Classification,MUSIC)算法用于圆柱共形阵列的DOA估计.文献[4]给出了一种基于加权MUSIC的共形阵列DOA估计算法.杨鹏等人提出通过内插投影技术,将共形阵列投影为平面阵列,而后利用平面阵列的MUSIC和旋转不变子空间(Estimation Of Signal Parameters Via Rotational Invariance Techniques,ESPRIT)等经典算法估计信号DOA[5-7].然而这些算法都将阵元方向图当作标量场处理,需要假设阵元辐射的极化特性一致.实际上大多数情况该假设均不成立.由于受到共形载体曲率的影响,共形阵列天线中各阵元具有独立的局部坐标系,使得共形阵列天线呈现多极化特性,在估计信号DOA时需要考虑阵元对来波信号的极化敏感的特性.文献[8]将信号极化参数和DOA作为待估计参数同时进行估计.但是该算法需要对所有待估计参数进行多维搜索,计算量庞大.文献[9]和[10]给出了锥形阵列和柱形阵列下的极化参数和DOA联合估计算法,并将其推广到相干源的情况[11].但该算法需要利用母线子阵列的线性特性,仅适用于单曲率共形阵列.文献[12]基于秩损理论提出了共形阵列天线信源方位与极化状态的联合估计算法.文献[13]将上述算法通过快速傅里叶变换(Fast Fourier Transform,FFT)变换到频域处理,有效降低了算法的计算量.文献[14]给出了任意共形阵列下极化参数和信号DOA的联合估计算法.但是很多情况下,我们仅仅关心信号的来波方向,对极化参数并不感兴趣.因此,有文献给出了共形阵列的盲极化DOA估计[15-17].通过对角参数与信号极化参数去耦合处理,实现了入射信号极化参数未知条件下的高分辨DOA估计.
上述方法大多是基于单馈源阵列,对交叉极化效应难以做到很好的抑制.双馈源天线构成的阵列除了能够实现单幅天线极化分集,有效提高信道利用效率,同时还能够很好地实现交叉极化效应的抑制以及灵活的极化控制[18].针对双馈源极化分集共形阵列的特点,本文通过信号极化分量的投影变换,给出了两个正交极化的信号等效导向矢量,将信号空间划分为两个正交极化信号子空间,并在此基础上构建该阵列下的信号模型.最后利用MUSIC算法实现了极化信号的DOA估计.该算法不需要对极化参数进行估计,能够同时对两个正交极化分量信号的DOA进行估计,最大估计信号数超过阵元数目,仿真实验验证了该算法的有效性.
1 理论分析
1.1极化分集共形阵列窄带信号模型
这里首先分析双馈源天线单元构成的共形阵列的接收信号模型.所谓双馈源天线单元是指,有两个馈源对该天线进行激励,并且每个馈源各自独立对该天线辐射的θ和φ两个正交极化分量进行激励[19],这样可以用同一幅天线实现极化分集,提高信道利用率.考虑一个N元的共形阵列,构建如图1所示的全局坐标系O(x,y,z)以及局部坐标系O(x′,y′,z′).假设方向(θ,φ)上入射的两个正交极化信号分别为为sθ(t)和sφ(t).

图1 共形阵列及其坐标系示意图
由于受到共形天线曲率影响,各个阵元方向图指向不一致.各个阵元方向图的θ和φ方向上的分量均在本地局部坐标系下定义,也不一致.因此要计算阵列对来波信号的响应,需要将来波信号的电场分量映射到各个阵元的局部坐标系.方向(θ,φ)在第i个阵元局部坐标系下的映射角度(θ′i,φ′i)可由下式计算:

式中,Rgli为全局坐标系到局部坐标系的欧拉旋转矩阵[20].为了方便计算信号在局部坐标系的映射分量,先将其变换到直角坐标系下,且有
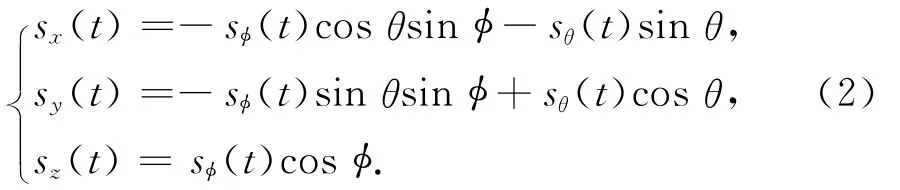
定义球坐标到直角坐标的变换矩阵Tsc(θ,φ)为

则,式(2)可以写为如下形式
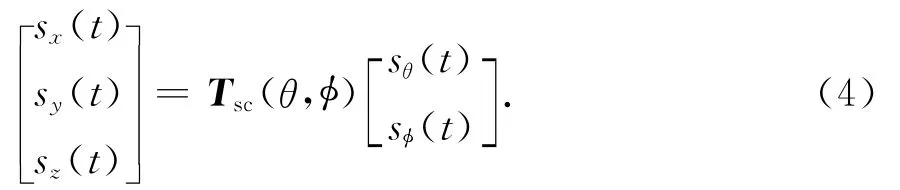
该信号在局部坐标下的映射分量为
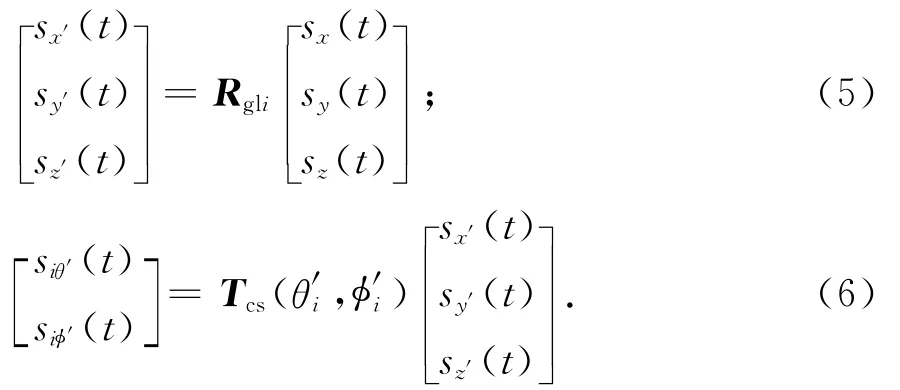
式中,Tcs(θ′i,φ′i)为直角坐标到球坐标的变换矩阵,
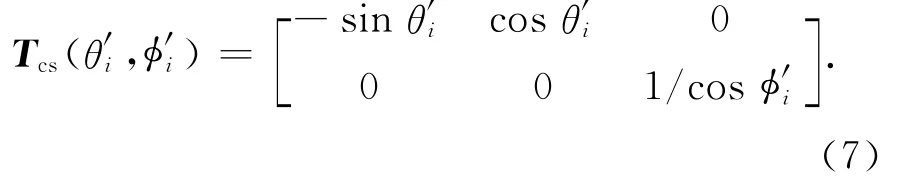
经过上面一系列变换,信号在第i个阵元上θ和φ方向上的电场分量为

定义第i个阵元的变换矩阵为Ti(θ,φ)=Tcs(θ′i,φ′i)RgliTsc(θ,φ),则来波信号在整个阵列上的映射分量为

阵列的接收信号实际上是各个天线单元对相应映射分量的响应,包含天线单元方向图增益和空间位置产生的时延两部分效应.不考虑阵元噪声,阵列接收信号可以用下式表示为
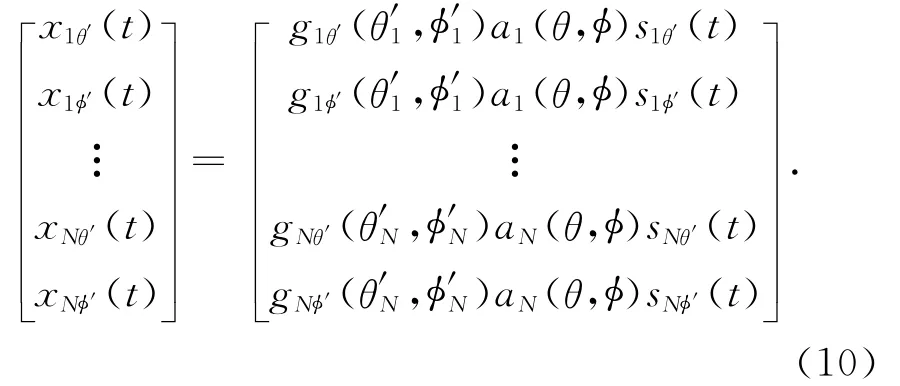
式中:giθ′(θ,φ)和giφ′(θ,φ)分别为第i个天线单元方向图在其局部坐标系下的θ方向和φ方向的分量;{·}′表示在各个天线单元的局部坐标系下定义的变量;ai(θ,φ)=ejkvie(θ,φ),其中k=2π/λ为相位常数,vi=[xi,yi,zi]T为第i个阵元的位置坐标矢量,e(θ,φ)=[cosθcosφ,sinθcosφ,sinφ]T为(θ,φ)方向上的单位矢量.阵列导向矢量a(θ,φ)为

则由式(9)和式(10)可得

式中:

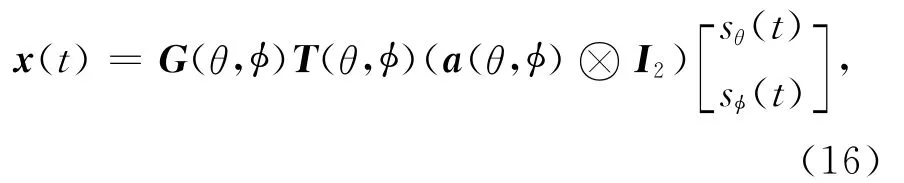
式中:T(θ,φ)=

“⊗”表示Kronecker积.定义

则接收信号为


前面考虑的是两个正交极化信号从同一个方向入射到共形阵列的情况.实际上对于极化分集系统,两个正交极化信道各自独立,正交极化信号的收发也能够做到各自独立进行,实现信道容量的扩展.假设有L个θ方向极化信号和M个φ方向极化信号入射到共形阵列,同时考虑接收通道噪声,此时各个极化信号的导向矢量和式(20)中的导向矢量类似,如图2所示,则阵列接收信号为
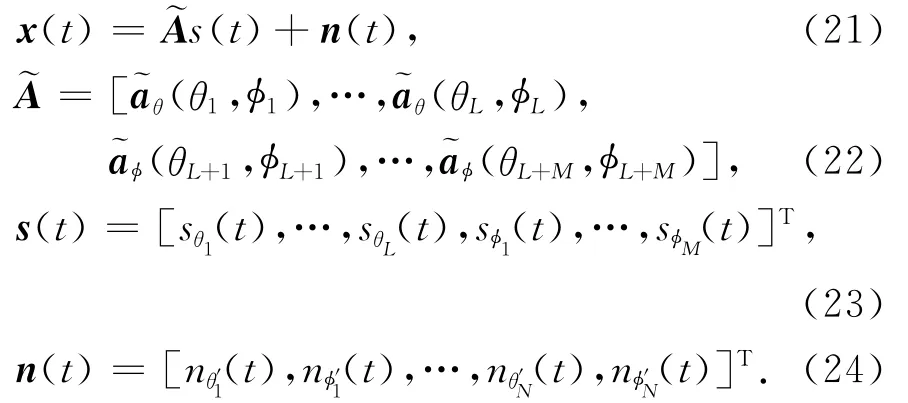

图2 阵列接收信号示意图
若系统采用圆极化方式,根据圆极化和线极化之间的关系,右旋圆极化(Right Hand Circular Polarization,RHCP)和左旋圆极化(Left Hand Circular Polarization,LHCP)信号可以由下式表达:

则

由式(27)和式(16)可得,此时阵列接收信号为
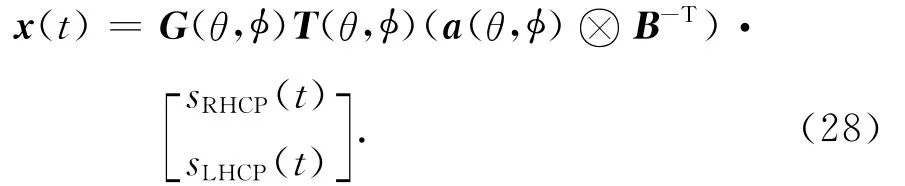
此时的等效导向矢量为

类似式(21),我们同样可以得到圆极化下的信号接收模型.
1.2共形阵列DOA估计
在得到阵列导向矢量的表达式后,很多需要知道阵列流形的DOA估计算法都可以直接应用.实际共形阵列中可能存在阵元间互耦、阵元幅度特性不一致、通道幅相特性不一致等误差.这些误差会导致实际阵列流形与理论不符,需要进行校正.这里不考虑这些因素,假设不存在阵列误差.MUSIC算法作为经典的DOA估计算法,在精确已知阵列导向矢量的前提下,能够很好地估计信号波达方向,适用与任意形式的阵列.有文献对其应用于共形阵列的性能进行了分析[21],这里将其扩展到极化信号的估计:

对信号协方差矩阵Rx进行特征值分解,得到噪声空间Un,即可利用下面的MUSIC空间谱对信号DOA进行估计:
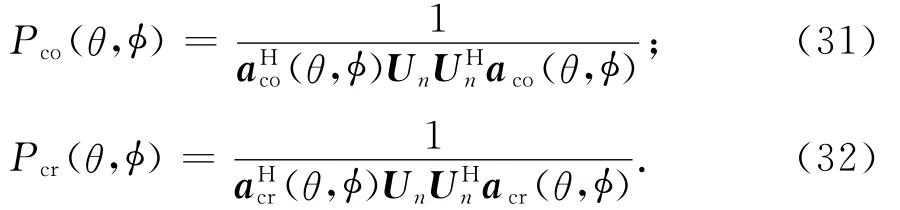
式中:Pco(θ,φ)和Pcr(θ,φ)分别表示同极化和交叉极化的空间谱;aco(θ,φ)和acr(θ,φ)为某种极化分集模式下的同极化和交叉极化的等效导向矢量(例如(θ,φ)和(θ,φ)或者RHCP(θ,φ)和LHCP(θ,φ).由于采用极化分集阵列,信号子空间分割为同极化和交叉极化两个子空间.两组正交极化的等效导向矢量分别张成各自的信号空间(Span{~aθ(θ1,φ1),…,~aθ(θL,φL)}和Span{~aφ(θ1,φ1),…,~aφ(θM,φM)}).分别对Pco(θ,φ)和Pcr(θ,φ)进行空域扫描即可得到极化分集下的正交极化信号的DOA估计值.
此外,由于采用双馈源天线单元,阵列导向矢量的维数扩展到2 N维,相应的信号空间也有所扩展.但是实际阵列的孔径并没有发生改变,故任意一个极化空间上所能够估计的信号个数最多仍然为N-1个.但由于该算法可以同时估计两个正交极化空间上的信号,所以最多能同时估计2 N-2个信号.
2 实验结果分析
前文给出了极化分集的共形阵列下的等效导向矢量模型,以及基于该模型的DOA估计算法.这里通过仿真实验来验证该算法的有效性.天线单元采用最低阶的圆形贴片天线模型[22],其方向图为

式中J0和J2分别为第一类零阶和二阶贝塞尔函数.系统采用左旋圆极化和右旋圆极化的分集方式,我们同时对两种极化方式信号的DOA进行估计.信噪比RSN定义为

式中:Ps为源信号s(t)的功率;Pn为阵列通道噪声功率.下面的仿真实验中假设各个源信号的功率相同且各自独立,各个通道的噪声功率也相同.
仿真实验一
考虑一个15元的均匀半圆弧阵列,相邻阵元间距为半波长.假设有4个RHCP信号和3个LHCP信号入射到该阵列,入射角度分别为[-38°,-13°,20°,42°]和[-56°,-7°,31°].角度扫描范围为[-90°,90°],信号的信噪比为5dB,快拍数为200.两个极化空间的空域谱如图3所示.

图3 接收7个信号的MUSIC空域谱
仿真实验二
前文分析了该算法理论上能够估计的最大信号数目为2 N-2.实际上当信号较多时,信号之间的角度间隔较小.受到阵列孔径和噪声等因素的影响,当信号角度间隔小于分辨极限时就无法再正确估计.因此实际能估计的信号数目通常要小于理论值.其他实验条件与仿真实验一相同,增加入射的信号数.假设有8个RHCP信号和8个LHCP信号入射到该阵列,入射角度分别为[-50°,-34°,-20°,-5°,8°,23°,40°,56°]和[-60°,-46°,-32°,-17°,-3°,14°,31°,50°].可以看到当信号数增加到16个时(超过阵元个数),文中算法仍然能够正确估计出各个信号的DOA.两个极化空间的空域谱如图4所示.

图4 接收16个信号的MUSIC空域谱
通过Monte-Carlo实验来验证算法的估计性能.我们用两种极化信号的DOA估计值的均方误差(ERMS)来作为衡量算法的估计精度的参数.
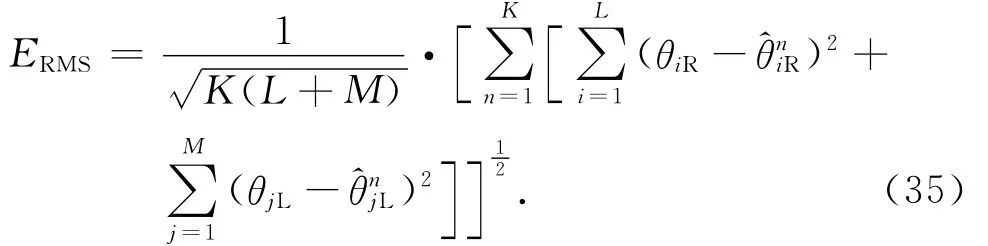
仿真实验三
为验证共形阵列曲率对DOA估计的影响,考虑一个30元的均匀圆环阵列,相邻阵元间距为半波长.假设有6个RHCP信号和6个LHCP信号入射到该阵列,入射角度分别为[-120°,-50°,0°,20°,95°,130°]和[-150°,-110°,-40°,22°,60°,115°].角度扫描范围为[-180°,180°],信号的信噪比为5dB,快拍数为200.两个极化空间的空域谱如图5所示.
仿真实验四
分别对15元半圆弧阵和30元均匀圆阵的DOA估计精度进行分析.假设有4个RHCP信号和3个LHCP信号入射到该阵列,入射角度分别为[-38°,-13°,20°,42°]和[-56°,-7°,31°].快拍数固定为200,信噪比RSN∈[-5dB,15dB],Monte-Carlo实验次数为K=100,根据式(35)计算估计的均方误差,实验结果如图6所示.
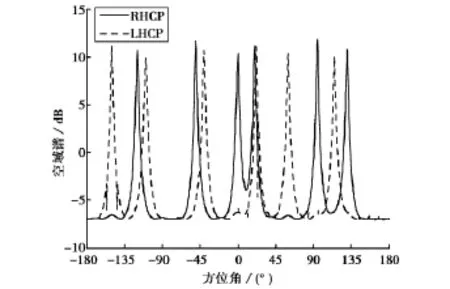
图5 30元圆环阵接收12个信号的MUSIC空域谱

图6 DOA估计的均方误差ERMS和信噪比RSN的关系曲线
仿真实验五
其他实验条件与仿真实验四相同,固定信噪比RSN=0dB,快拍数在[100,1 000]上取值,Monte-Carlo实验次数为K=100,根据式(35)计算估计的均方误差,实验结果如图7所示.

图7 DOA估计的均方误差ERMS和快拍数的关系曲线
由上面的仿真实验可以看出,本文给出的DOA估计算法能同时对两种正交极化的信号进行估计.同时估计的信号数目甚至能够超过阵元的个数.在较低的信噪比和较少的快拍数的情况下就能够很好地估计出信号的来波方向.算法估计的误差随着信噪比和快拍数的增加迅速减小.对于某个信号而言,由于受到共形阵列曲面曲率的影响,实际有效的接收阵元仅仅是该方向上阵元方向图增益不为零的一部分.对于30元均匀圆阵,任意方向的信号均有15个有效接收阵元,而15元的半圆弧阵,部分信号的有效接收阵元小于15个,因此估计误差略高于圆阵.
同时,由于将两个正交极化信号在信号子空间上进行了分离,构成的空域谱也各自独立.因此,对于两个正交极化的信号具有极高的分辨率,这一点在前面的实验结果已经得到了验证.
此外,虽然本文提出的算法是针对正交极化分集的信号,但是一般极化信号也可以写成两个正交极化分量合成的形式,因此本文的算法同样可以进行估计.但是这样的信号由于在两个正交的极化信号空间均存在分量,需要将其视为两个信号进行估计,得到估计角度以后再将两个正交极化信号空间的角度估计结果合并即可.
3 结 论
通过分析双馈源极化分集共形阵列的特点,构建了正交极化信号在共形阵列下的接收信号模型.给出了极化分解下两个正交极化信号空间的等效阵列导向矢量.在此基础上,提出了基于MUSIC算法的共形阵列极化信号DOA估计.该算法能够同时估计正交极化分集信号的波达方向.同时由于将原信号空间拓展为两个正交极化分集的信号空间,能够估计的最大信号数目超过阵元个数.对于一般极化信号,该算法也能通过估计该信号的两个正交极化分量的DOA来得到该信号的波达方向,无需估计极化参数.仿真实验表明该算法在较低的信噪比和快拍数下仍然具有良好的估计性能.
[1] JOSEFSSON L,PERSSON P.Conformal Array Antenna Theory and Design[M].Piscataway:IEEE Press,2006:1-70.
[2] KIM K,SARKAR T K,WICKS M C,et al.DOA estimation utilizing directive elements on a conformalsurface[C]//Proceedings of IEEE Radar Conference.Huntsville,2003:91-96.
[3] 杨永建,王晟达,马 健,等.基于MUSIC算法的圆柱共形阵DOA估计[J].空军工程大学学报:自然科学版,2012,13(5):66-70.
YANG Yongjian,WANG Shengda,MA Jian,et al.DOA estimation for cylindrical conformal array antenna based on MUSIC algorithm[J].Journal of Air Force Engineering University:Natural Science,2012,13(5):66-70.(in Chinese)
[4] PENG Y,FENG Y,NIE Z P.DOA estimation using MUSIC algorithm on a cylindrical conformal array[C]//IEEE Antennas and Propagation Society International Symposium.Honolulu,2007:5299-5302.
[5] YANG P,YANG F,NIE Z P.DOA estimation with sub-array divided technique and interporlated ESPRIT algorithm on a cylindrical conformal array antenna[J].Progress in Electromagnetics Research,2010,103:201-216.
[6] 杨 鹏,杨 峰,聂在平,等.基于共形天线阵的免搜索来波方向估计算法研究[J].电波科学学报,2012,27(2):421-425.YANG Peng,YANG Feng,NEI Zaiping.Search-free
DOA estimation algorithm based on conformal antenna array[J].Chinese Journal of Radio Science,2012,27(2):421-425.(in Chinese)
[7] 杨 鹏,杨 峰,聂在平,等.基于圆柱共形阵的快速来波方向估计[J].电波科学学报,2012,27(1):61-65.YANG Peng,YANG Feng,NEI Zaiping,et al.Fast
DOA estimation algorithm based on cylindrical conformal array[J].Chinese Journal of Radio Science,2012,27(1):61-65.(in Chinese)
[8] 刘 帅,周洪娟,金 铭,等.锥面共形阵列天线的极化-DOA估计[J].系统工程与电子技术,2012,34(2):253-257.
LIU Shuai,ZHOU Hongjuan,JIN Ming,et al.Polarization-DOA estimation for conical conformal array antennas[J].Systems Engineering and Electronics,2012,34(2):253-257.(in Chinese)
[9] 张树银,郭 英,齐子森.锥面共形阵列信源方位和极化参数的联合估计算法[J].电子与信息学报,2011,33(10):2407-2412.
ZHANG Shuyin,GUO Ying,QI Zisen.Jiont estimation of 2DDOA and polarization with conical conformal array antenna[J].Journal of Electronics &Information Technology,2011,33(10):2407-2412.(in Chinese)
[10] 张树银,郭 英,齐子森.柱面共形阵列信源方位与极化状态的联合估计算法[J].电波科学学报,2011,26(6):1118-1125.
ZHANG Shuyin,GUO Ying,QI Zisen.Jiont estimation of DOA and polarization with cylindrical conformal array[J].Chinese Journal of Radio Science,2011,26(6):1118-1125.(in Chinese)
[11] 齐子森,郭 英,王布宏,等.柱面共形阵列天线盲极化波达方向估计算法[J].电波科学学报,2011,26(2):245-252.
QI Zisen,GUO Ying,WANG Buhong,et al.Blind DOA estimation algorithm for cylindrical conformal array with respect to polarization diversity[J].Chinese Journal of Radio Science,2011,26(2):245-252.(in Chinese)
[12] 齐子森,郭 英,王布宏,等.共形阵列天线信源方位与极化状态的联合估计算法[J].电子学报,2012,40(12):2562-2566.
QI Zisen,GUO Ying,WANG Buhong,et al.Joint DOA and polarization estimation algorithm for conformal array antenna[J].Acta Electronica Sinica,2012,40(12):2562-2566.(in Chinese)
[13] YANG P,YANG F,NIE Z P,et al.Fast 2-d DOA and polarization estimation using arbitrary conformal antenna array[J].Progress in Electromagnetics Research C,2012,25:119-132.
[14] COSTA M,RICHTER A,KOIVUNEN V.DOA and polarization estimation for arbitrary array configurations[J].IEEE Transactions on Signal Processing,2012,60(5):2330-2343.
[15] QI Z,GUO Y,WANG B,et al.DOA estimation algorithm for conical conformal array antenna[C]//IET International Radar Conference.Xi’an,2009:1-4.
[16] 齐子森,郭 英,姬伟峰,等.锥面共形阵列天线盲极化DOA估计算法[J].电子学报,2009,37(9):1919-1925.
QI Zisen,GUO Ying,JI Weifeng,et al.Blind DOA estimation algorithm f or conical con formal array antenna with respect to polarization diversity[J].Acta Electronica Sinica,2009,37(9):1919-1925.(in Chinese)
[17] QI Z,GUO Y,WANG B.Blind direction-of-arrival estimation algorithm for conformal array antenna with respect to polarisation diversity[J].IET Microwaves,Antennas and Propagation,2011,5(4):433-442.
[18] DIETRICH C B,DIETZE K,NEALY J R,et al.Spatial,polarization,and pattern diversity for wireless handheld terminals[J].IEEE Trans on Antennasand Propagation,2001,49(9):1271-1281.
[19] DOHMEN C,ODENDAAL J W,JOUBERT J.Synthesis of conformal arrays with optimized polarization[J].IEEE Transactions on Antennas and Propagation,2007,55(10):2922-2925.
[20] MILLIGAN T.More applications of Euler rotation angles[J].IEEE Antennas and Propagation Magazine,1999,41(4):78-83.
[21] QI Z,GUO Y,WANG B,et al.Performance analysis of MUSIC for conformal array[C]//IEEE International Conference on Wireless Communications,Networking and Mobile Computing.Shanghai,2007:168-171.
[22] JAMES J R,HALL P S,WOOD C.Microstrip Antenna Theory and Design[M].New York:Peter Peregrinus,1981:67-109.
Direction of arrival estimation for conformal array with polarization diversity
LIU Chao DING Zhizhong
(Hefei University of Technology,Hefei Anhui 230009,China)
A blind polarization direction of arrival(DOA)estimation method is presented based on the dual feed conformal array for polarization diversity signals.Through the projection and Euler rotation transformation,the equivalent steering vectors for copolarization and cross-polarization signals are given out.The signal space is divided into the co-polar and cross-polar signal subspace,and the blind polarization separation of the two orthogonal polarization signals is realized.Based on this signal model,multiple signal classification(MUSIC)based method is proposed here to estimate the co-polar and cross-polar signal simultaneously without the estimation of polarization parameters.The maximum number of signal that can be estimated may exceed the element number.Simulation results illustrate the good performance of our method.
conformal array;polarization diversity;DOA estimation;MUSIC

TN821+.91
A
1005-0388(2015)02-0274-08

刘 超(1981-),男,湖北人,博士,合肥工业大学讲师,硕士生导师,主要研究方向为阵列信号处理、通信信号处理.

丁志中(1961-),男,安徽人,博士,合肥工业大学教授,硕士生导师,主要研究方向为新一代无线通信网技术、Ad hoc网络关键技术、车联网关键技术等.
刘 超,丁志中.极化分集下的共形阵列波达方向估计[J].电波科学学报,2015,30(2):274-281.
10.13443/j.cjors.2014041501
LIU Chao,DING Zhizhong.Direction of arrival estimation for conformal array with polarization diversity[J].Chinese Journal of Radio Science,2015,30(2):274-281.(in Chinese).doi:10.13443/j.cjors.2014041501
2014-04-15
博士后基金(20100480680);安徽省自然科学基金(1208085QF105)
联系人:刘超E-mail:disneyl@mail.ustc.edu.cn

