微扰法结合最小二乘支持向量机反演土壤湿度
张清河 徐 飞 邹启源
微扰法结合最小二乘支持向量机反演土壤湿度
张清河 徐 飞 邹启源
(三峡大学理学院,湖北宜昌443002)
将最小二乘支持向量回归技术应用到土壤湿度反演研究.利用微扰法数值模拟不同雷达参数下裸露土壤微波后向散射特性.经过数据敏感性分析,选取雷达频率为L波段(1.4GHz),双入射角(40°、50°),并设计多种反演方案,分别以单极化、双极化及同极化后向散射系数比值作为微波信号样本信息,经过适当的训练,利用最小二乘支持向量回归技术对土壤含水量进行了反演研究.结果表明:当采用多入射角、同极化后向散射系数比值作为微波信号样本信息时,反演结果具有较高的精度.同时,经过与人工神经网络结果比较,证明了该方法的有效性及抗噪声能力,为土壤湿度的实时反演研究提供了一种新方法.
微扰法;土壤湿度反演;最小二乘支持向量机
引 言
土壤湿度反演是气象学、土壤学、水文学、生态学等领域所关注和研究的重要内容,确定土壤湿度是对地遥感的最主要任务之一.在众多对地遥感方式中,微波遥感由于具有全天时、全天候的特点,并对云雾、雨雪、植被及地表有一定的穿透能力,在农业、林业、环境、水文等应用领域显示出无可比拟的优势[1].
近二十年来,已有许多学者利用雷达数据对土壤湿度进行了反演研究,取得了重要进展.早期的土壤湿度反演方法多采用经验公式法和基于理论模型的优化迭代方法,取得了一定的效果.经验公式方法的代表如Dubois模型[2]、Oh模型[3]、Shi模型[4]等.该方法依据一定条件下的实验数据,直接建立地表参数与雷达后向散射系数间的线性回归方程.其主要优点是简单、直接,但由于获取实验数据的区域限制性,经验公式方法的适用范围有限.也有研究者采用基于理论模型的优化迭代方法,这种方法一般先基于一种微波地表散射理论模型,数值模拟不同频率、不同极化、不同入射角下不同地表参数的后向散射系数,通过与实测雷达数据对比,构造合适的代价函数,然后借助数学优化迭代方法进行反演计算.该方法的优点是理论基础完备,具有较高的适应性,但该方法比较复杂,反演模型中包含的未知参数较多.如Bindlish等[5]利用积分方程模型(Integral Equation Model,IEM)和雷达数据采用Jacobian矩阵迭代方法获取地表参数;Rao等[6]提出了线性统计回归模型;Njoku等[7]提出的针对AMSR-E数据的土壤湿度反演迭代方法Leveberg-Marquardt算法等.还有的学者借助于遗传算法,通过对代价函数的最小化,达到反演地表参数的目的[8-9].另外,也有学者通过一定的理论模型,先构建微波信号与土壤湿度的网格图或曲线族,再由遥感数据通过查网格图或曲线族得到对应的土壤湿度[10-11].人工神经网络(Artificial Neural Network,ANN)具有良好的非线性映射能力,近几年逐渐被应用在微波遥感土壤湿度反演研究中[12-13].但利用人工神经网络方法来建模还存在许多待解决的问题,特别是神经网络的局部最小值问题和网络拓扑结构确定问题.
近年来在统计学习理论(Statistical Learning Theory,SLT)[14]框架基础上发展了一种新的通用学习方法——支持向量机(Support Vector Machine,SVM)[15].与人工神经网络相比,SVM较好地解决了小样本、非线性、高维数、局部极小点等实际问题,具有很好的泛化能力,能以任意的精度逼近任意函数[16].同时,SVM的拓扑结构由支持向量决定,避免了传统神经网络拓扑结构需要经验试凑的方法.近年来,已有学者利用SVM技术进行了一些应用研究,如非线性系统辩识[16]、金融时间序列预测[17]、故障诊断[18]、电磁逆散射[19]等.
本文利用最小二乘支持向量机(Least Squares Support Vector Machine,LS-SVM)方法对土壤湿度反演问题进行研究.与标准SVM相比,LS-SVM用等式约束代替不等式约束,求解过程转变成解一组等式方程,求解速度相对加快.以微扰法(Small Perturbation Method,SPM)作为理论模型,并根据SPM中同极化后向散射系数的比值与地表粗糙度参数无关的特性,数值模拟了同极化后向散射系数比值在不同雷达入射角下随土壤湿度的变化关系特性,经过敏感性分析,选择合适的数据并以此作为训练样本提供给LS-SVM训练学习,建立好反演模型后,对土壤湿度进行了实时反演.
1 理论分析
1.1土壤粗糙面散射模型及敏感性分析
土壤表面可看作随机粗糙面,相应的粗糙面电磁波散射模型有:SPM模型、基尔霍夫近似模型(Kirchhoff Approximation Model,KAM)、双谱模型(Bispectrum Model,BSM)[1]及IEM等[20].双谱模型和积分方程模型的有效范围比较宽,但涉及参数过多,且参数之间的耦合关系比较复杂,因而反演土壤湿度比较困难[11].在基尔霍夫模型中,同极化后向散射系数相同,而交叉极化后向散射系数为零,这在利用多极化微波信号遥感土壤湿度方面是不利的.而微扰法的理论推导比较严格,当满足条件时,理论模型与实测数据吻合得较好.
一般地,当粗糙面为微小起伏时,满足[1]

式中:k是自由空间波数;σ、l分别是粗糙面的均方根高度和相关长度.微扰法给出的两个同极化后向散射系数σ0vv和σ0hh分别为[1]
式中:θ是入射角;εr是表层土壤的复介电常数;W(2ksinθ,0)是表面起伏相关函数的Fourier变换;R‖和R⊥分别是平土壤表面的水平极化和垂直极化Fresnel反射系数,其值由入射角θ和土壤的复介电常数εr决定.
土壤湿度的变化会引起土壤后向散射系数的变化,这是主动微波遥感测量土壤湿度的物理基础.同时,土壤的散射特性也与其粗糙度密切相关.大多数情况下,土壤湿度和粗糙度的变化都能引起后向散射系数的变化.针对裸露地表微波遥感试验,测得雷达后向散射系数与土壤湿度有着直接关系,且可表示成如下函数形式为
式中:R代表地表粗糙度;α代表微波信号对土壤湿度的敏感性;mv是单位体积土壤含水量.
由于土壤湿度和粗糙度的变化都能引起后向散射系数的变化,因此,如何从微波信号中消除地表粗糙度影响及准确提取土壤湿度信息一直是土壤湿度反演中的一个关键问题.研究表明,通过正确选择雷达传感器参数或采用多频率、多极化、多入射角数据,可以建立模型消除地表粗糙度的影响,提高反演精度.为此将微扰法中两个同极化后向散射系数相除,得到其比值为[11]

该模型仅取决于入射角θ和土壤的复介电常数εr,而与地表粗糙度参数无关.这一特性可表示为

由于式(5)已与地表粗糙度无关,所以微波信号对土壤湿度的敏感性α就只与雷达传感器参数(频率、入射角、极化)及土壤湿度的大小有关.当采用式(5)作为土壤湿度反演模型时,重点就要对入射角θ进行敏感性分析,期望找到在合适的雷达入射角θ参数下,σ0vv/σ0hh对土壤湿度有较高的敏感性.图1(a)、(b)分别给出了在L波段(f=1.4GHz),不同入射角θ下,比值σ0vv/σ0hh随土壤体积含水量mv的变化情况.其中,图1(a)、(b)分别对应两种不同的土壤结构成分:S=51.51%,C=13.43%(沙壤土);S=17.16%,C=19.00%(粉砂壤土),S,C分别代表土壤中沙土和粘土的百分比例.土壤的介电模型采用Hallikainen模型[20].
从图1(a)、(b)来看,对于不同的土壤结构成分,(σvv/σhh)~mv曲线基本上保持了相同的变化趋势,入射角较大时(如60°,70°),曲线对mv比较敏感,当体积含水量从2%增加到50%时,σ0vv/σ0hh能产生7~9dB的变化,特别是在低含水量情况下,这一特性表现得尤为明显.入射角较小时,曲线对mv不敏感,基本上保持不变.为了使比值σ0vv/σ0hh对含水量mv保持较高的敏感性,保证反演的精度,原则上应该选取较高的雷达入射角,但当入射角θ≥70°时,散射模型准确度不高,且后向散射较弱,而且在高入射角(大于60°)情况下,地表粗糙度的变化会引起后向散射系数的显著变化,从而影响mv的反演精度.所以在本文的研究中,雷达入射角选取40°~60°,并利用式(5)数值模拟不同土壤湿度下的同极化后向散射系数比值,并以此作为训练样本对SVM进行训练学习.
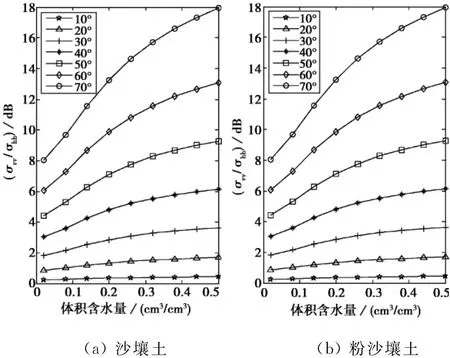
图1 不同土壤类型下σ0vv/σ0hh与mv的关系曲线
1.2最小二乘支持向量机(LS-SVM)
LS-SVM是SVM的一种改进,它是将传统SVM中的不等式约束改为等式约束,把解二次规划问题转化为求解线性方程组问题,提高了求解问题的速度和收敛精度.设样本为n维向量,可表示为(x1,y1),…,(xl,yl)∈Rn×R,样本总数为l.x为输入数据,代表传感器所接收到的微波信号,如土壤后向散射系数,当采用多雷达频率、多入射角及极化的微波数据时,x为多维空间参数.y为输出数据,代表相应的土壤湿度.首先用一非线性映射ψ(·)把样本从原空间Rn映射到特征空间φ(xi),从而在高维特征空间中构造最优决策函数[16]

利用结构风险最小化(Structural Risk Minimization,SRM)原则,寻找权向量ω和偏差量b,即最小化目标函数:
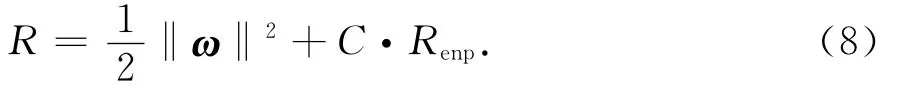
式中:‖ω‖2为控制模型复杂度的参数;C是正规化参数,控制对超出误差样本的惩罚程度;Renp为误差控制函数,即ε不敏感损失函数.引入松弛因子ξi,回归问题表示成如下约束优化问题
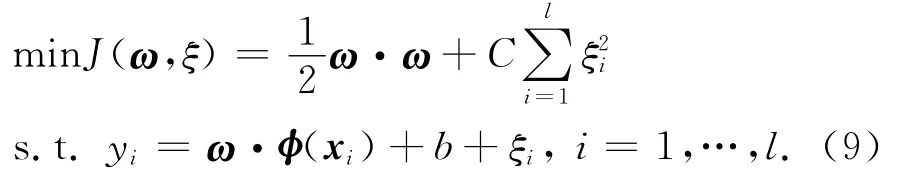
采用拉格朗日乘子法,并定义核函数K(xi,xj)=φ(xi)·φ(xj),优化问题转化为求解如下线性方程组为

式中:1v=[1;…;1];α=[α1;…;αl],αi(i=1,…,l)是拉格朗日乘子;y=[y1;…;yl];Ωi,j=(φ(xi))Tφ(xj),i,j=1,2,…,l.
最后用最小二乘法求出α和b,LS-SVM也由此得名,并且得到非线性预测模型

常用的核函数包括多项式核、多层感知(Multilayer Perception,MLP)核、径向基(Radial Basis Function,RBF)核等.本文采用RBF作为核函数,其形式为K(x,xi)=exp(-‖x-xi‖2/σ2),其中σ为核参数.
1.3训练样本模拟及反演方案设计
与人工神经网络一样,在基于LS-SVM的参数反演问题中,首先要用训练样本对LS-SVM进行训练,从而建立反演模型.本文中的训练样本采用SPM数值模拟得到,在SPM模型中,输入参数包括传感器雷达参数(频率、入射角、极化等)和地表参数(含水量、均方根高度、相关长度等).大量研究表明,低频微波信号对土壤湿度的敏感性比高频显得尤为突出,所以本文选取雷达频率为f=1.4GHz(L波段),依据前文的敏感性分析,雷达入射角取为40°、50°,并以同极化后向散射系数比值σ0vv/σ0hh作为LSSVM训练样本信息,考虑通过多极化、多入射角数据的组合,提高反演精度.需要说明的是,在实际的主动微波遥感土壤湿度研究方面,微波传感器接收到的是粗糙地表同极化后向散射系数(如σ0vv、σ0hh)或交叉极化后向散射系数(如σ0vh、σ0hv),而不是同极化后向散射系数的比值σ0vv/σ0hh.也就是说,比值σ0vv/σ0hh并不是直接由式(5)计算得到,而是先用SPM数值计算地表同极化后向散射系数σ0vv和σ0hh,再得到其比值,并以此作为微波信号来实现土壤湿度的反演.表1是本文研究中地表参数的变化范围及步长值,并假设土壤中沙土和粘土的百分比例分别为:S=42%,C=18%.这些参数不仅位于SPM模型的有效范围内,而且覆盖了大多数自然地表的参数状况.由这些地表参数并经SPM数值模拟,得到约892个训练样本.

表1 SPM数值模拟输入参数变化范围
2 数值结果与分析
将样本分为训练样本和测试样本,其中训练样本640个,用于对SVM进行训练学习,建立土壤湿度反演模型.剩余的252个测试样本用来检验该方法反演土壤湿度的精度.
首先研究单极化、多入射角下,LS-SVM方法对土壤湿度的反演情况,分别以多入射角(40°、50°)下的σ0vv和σ0hh作为LS-SVM的输入,对LS-SVM进行训练.图2(a)、(b)分别给出了LS-SVM的反演值与真实值的比较结果.
从图2的比较来看,结果显然是不理想的,其相关系数(R2)和均方根误差(Root Mean Squared Error,RMSE)分别为0.633 4、10.64%(VV极化)和0.594 2、11.02%(HH极化).作为比较,在相同的“条件”下(相同的训练样本、相同的测试样本),本文利用人工神经网络方法对土壤湿度进行了反演研究.在该方法中,采用Matlab中神经网络工具箱所提供的三层BP神经网络(Back Propagation Neural Network,BPNN),BP网络训练算法为L-M训练算法,隐含层激活函数为对数型sigmoid函数.基于BPNN的反演结果为0.679 4、10.03%(VV极化)和0.593 4、11.05%(HH极化).从比较来看,虽然两种方法的反演结果各有千秋,但其精度都较低,这也说明当采用单一极化后向散射系数时,由于训练样本信息的不完善,这两种方法都不能很好地建立起土壤湿度与微波信号之间的非线性关系,对土壤湿度的反演达不到理想的精度.
图3是同时采用双极化后向散射系数(σ0vv和σ0hh)作为样本信息时,LS-SVM给出的土壤湿度的反演值与实际值的比较结果.其相关系数和均方根误差分别为0.992 4和1.70%.与图2比较,可以看出当采用双极化后向微波信号时,由于增加了一个同极化后向微波信号,丰富了训练样本信息,提高了基于LS-SVM的反演建模精度,使得土壤湿度的反演精度有了大幅提高.

图2 采用单极化后向散射系数时基于LS-SVM的土壤湿度反演结果

图3 采用双极化后向散射系数时基于LS-SVM的土壤湿度反演结果
其次,以同极化后向散射系数比值σ0vv/σ0hh作为LS-SVM的输入,在相同的训练样本和测试样本情况下,研究了LS-SVM对土壤湿度的反演情况.图4是反演值与真实值的比较.从图4来看,反演值与真实值非常接近,其相关系数几乎为1,均方根误差为0.035%.与前两种反演方案相比较,由于采用同极化后向散射系数比值σ0vv/σ0hh作为样本信息,从微波信号中消除了地表粗糙度的影响,提高了微波信号对土壤湿度的敏感性,使得土壤湿度的反演达到了一个很高的精度.同样的,在相同的“条件”下,基于BPNN的反演结果的均方根误差为0.09%.可以看出,LS-SVM的反演精度要优于人工神经网络方法,这也表明了前文所说的SVM的泛化能力要优越于神经网络等传统学习方法.
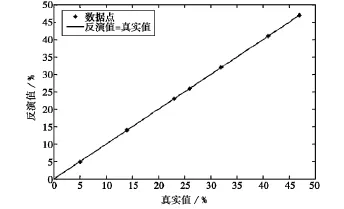
图4 采用同极化后向散射系数比值时基于LS-SVM的土壤湿度反演结果
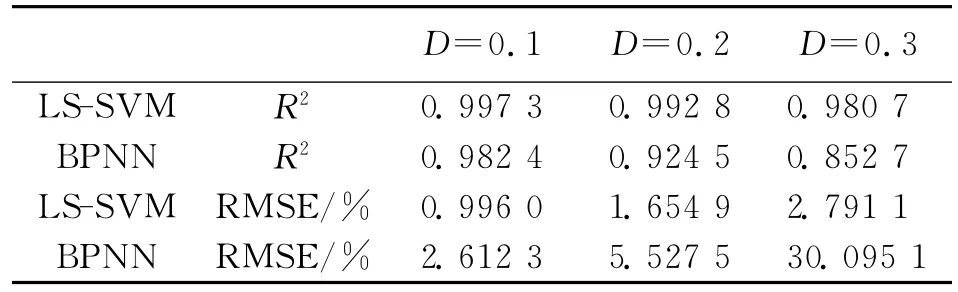
表2 LS-SVM与BPNN两种方法反演结果误差比较
最后,讨论LS-SVM方法的抗噪声性能.因为在实际应用中,传感器所接收的数据不可能就是数值模拟的数据,还可能包含各种各样的噪声和误差.为了模拟实际应用中的电磁环境,对上例中的样本数据(同极化后向散射系数比值)加上高斯随机噪声(设高斯随机噪声的偏差为D),再以此作为LSSVM的输入,从而得到加噪后的基于LS-SVM的土壤湿度反演结果.表2是不同D时,LS-SVM与BPNN两种方法反演结果的误差比较.从表中可以看出,随着噪声的增大,两种方法的反演精度都在降低,特别是BPNN方法,这一趋势尤其明显,但对于LS-SVM方法,下降的幅度是有限的,且仍然保持在一个较高的精度上,这也说明LS-SVM方法比BPNN方法有更好的泛化能力和抗噪声性能.
3 结 论
本文主要研究了基于最小二乘支持向量回归技术的土壤湿度反演方法.通过微扰法数值模拟了不同雷达参数下裸露土壤微波后向散射特性.经过数据敏感性分析,选取雷达频率为L波段,双入射角(40°、50°),设计了多种反演方案,分别以单极化、双极化及同极化后向散射系数比值作为微波信号样本信息,利用最小二乘支持向量回归技术对土壤含水量进行了反演研究.研究结果表明:在多种反演方案中,以同极化后向散射系数比值作为样本信息时,土壤湿度的反演精度是最高的;LS-SVM方法比人工神经网络方法有更好的泛化能力和抗噪声性能.下一步的工作将研究基于被动或主被动相结合的土壤湿度人工智能反演方法.
[1] ULABY F T,MOORE R K,FENG J C.Microwave Remote Sensing(VolumeⅡ)[M].Beijing:Science Press,1987.
[2] DUBOIS P C,ZYL J J,ENGMAN T.Measuring soil moisture with imaging radar[J].IEEE Trans Geosci Remote Sens,1995,33(4):915-926.
[3] OH Y,SARABANDI K,ULABY F T.An empirical model and inversion technique for radar scattering from bare soil surface[J].IEEE Trans Geosci Remote Sens,1992,30(2):370-382.
[4] SHI J C,WANG J,HSU A Y,et al.Estimation of bare surface soil moisture and surface roughness parameter using L-band SAR image data[J].IEEE Trans Geosci Remote Sens,1992,35(5):1254-1266.
[5] BINDISH R,BARROS A P.Multifrequency soil moisture inversion from SAR measurements with the use of IEM[J].Remote Sens Environ,2000,71(1):67-88.
[6] RAO K S,RAJU S,WANG J R.Estimation of soil moisture and surface roughness parameters from backscattering coefficients[J].IEEE Trans Geosci Remote Sens,1993,31(3):1094-1099.
[7] NJOKU E G,LI L.Retrieval of land surface parameters using passive miceowave measurements at 6-18 GHz[J].IEEE Trans Geosci Remote Sens,1999,37(1):79-93.
[8] 王悦泉,金亚秋.陆地表面粗糙度和土壤湿度多维参数同时反演的遗传算法[J].遥感学报,2000,4(2):90-94.
WANG Yuequan,JIN Yaqiu.A genetic algorithm to simultaneously retrieve land surface roughness and soil moisture[J].Journal of Remote Sensing,2000,4(2):90-94.(in Chinese)
[9] 庞自振,廖静娟.基于遗传算法和雷达后向散射系数的地表参数反演研究[J].遥感技术与应用,2008,23(2):130-141.
PANG Zizhen,LIAO Jingjuan.The study of retrieving surface parameters based on genetic algorithm and backscattering models[J].Remote Sensing Technology and Application,2008,23(2):130-141.(in Chinese)
[10] 黄兴忠,金亚秋.利用主被动遥感数据估算土壤湿度和粗糙度的新方法[J].电波科学学报,1996,11(1):27-32.
HUANG Xingzhong,JIN Yaqiu.A simple method for the estimation of the soil wetness and surface roughness by using active/passive microwave data[J].Chinese Journal of Radio Science,1996,11(1):27-32.(in Chinese)
[11] 李宗谦,冯孔豫.从雷达后向散射系数反演土壤湿度与复介电常数[J].中国科学(E辑),1997,27(3):243-248.
LI Zongqian,FENG Kongyu.Inversion of soil moisture and complex dielectric constant from radar backscattering coefficient[J].Science in China(Series E),1997,27(3):243-248.(in Chinese)
[12] NOTARNICOLA C,ANGIULLI M,POSA F.Soil moisture retrieval from remotely sensed data:neural network approach versua Bayesian method[J].IEEE Trans Geosci Remote Sens,2008,46(2):547-557.
[13] ZHAO K G,SHI J C,ZHANG L X,et al.Retrieval of bare soil surface parameters from simulated data using neural networks combined with IEM[C]//Geoscience and Remote Sensing Symposium,2003.
[14] VAPNIK V.Statistical Learning Theory[M].New York:Wiley,1998.
[15] CRISTIANINI N,TAYLORJ S.An Introduction to Support Vector Machine[M].Cambridge:Cambridge Univ Press,2000.
[16] DREZET P M L,HARRISON R F.Support vector machines for system identification[C]//UKACC International Conference,1998,1:688-692.
[17] VAN GESTEL T,SUYKENS J A K,BAESTAENS D,et al.Financial time series prediction using least squares support vector machines within the evidence framework[J].IEEE Trans Neural Networks,2001,12(4):809-821.
[18] YUAN S F,CHU F L.Support vector machinesbased fault diagnosis for turbo-pump rotor[J].Mechanical Systems and Signal Processing,2006,20(4):939-952.
[19] 张清河,汪 洋,陈将宏.基于支持向量机的复合柱体目标参数反演[J].电波科学学报,2012,27(6):1232-1237.
ZHANG Qinghe,WANG Yang,CHEN Jianghong.Composite conducting-dielectric cylinder parameters reconstruction by means of SVM[J].Chinese Journal of Radio Science,2012,27(6):1232-1237.(in Chinese)
[20] FUNG A K,LI Z,CHEN K S.Backscattering from a randomly rough dielectric surface[J].IEEE Trans Geosci Remote Sens,1992,30(2):356-369.
[21] HALLIKAINEN M T,ULABY F T,DOBSON M C,et al.Microwave dielectric behavior of wet soil—PartⅠ:empirical models and experimental observa-tions[J].IEEE Trans Geosci Remote Sens,1985,23(1):25-34.
第25届全国电磁兼容学术会议(EMC’2015/北京)征文通知
中国电子学会电磁兼容分会与中国通信学会电磁兼容委员会决定于2015年6月3日至6月5日在北京联合举办第25届全国电磁兼容学术会议(EMC'2015/北京),欢迎广大专家学者踊跃投稿出席会议。
征文范围如下:
1.电磁场理论
2.传输线和电缆
3.串扰与耦合
4.散射
5.天线、探头、传感器
6.电波传播
7.电磁干扰源
8.电磁环境
9.电磁生物效应
10.电磁计算、建模及仿真
11.频谱管理
12.电磁兼容标准、规程
13.静电、雷电及电磁脉冲
14.地震电磁学
15.信号完整性
16.屏蔽、滤波及接地
17.抗扰度及敏感度
18.电磁干扰预测分析、抑制技术
19.通信中的电磁兼容
20.汽车、电力工程中的电磁兼容
21.高速铁路的电磁兼容
22.暗室、混响室、吸波材料
23.电磁兼容测量
注意事项:
1.来稿应是来公开发表有新意的学术论文,并请用电子文档按正规学报格式双栏排版,篇幅不得超过A4纸6页。
2.作者信息请另页发送(含姓名、单位、职称、电话等)。
3.录用的论文必须到会宣读,宣读后由国家正式机构出版,来宣读的论文不予出版。
联系人:石 丹18601206662 张苏慧13661343833
中国电子学会电磁兼容分会
中国通信学会电磁兼容委员会
2014.12
Inversion of bare soil moisture by the least squares support vector machine approach combined with SPM
ZHANG Qinghe XU Fei ZOU Qiyuan
(College of Science,Three Gorges University,Yichang Hubei 443002,China)
The least squares support vector machine(LS-SVM)techniques are applied to the inversion of soil moisture.The backscattering properties of bare soil under different radar parameters are numerically simulated by using small perturbation method(SPM).After data sensitivity analysis,with the L-band radar frequency(1.4GHz)and dual angle of incidence(40°/50°)selected,designed a variety of inversion scheme,herein the single polarization,dual polarization and co-polarization ratio of the backscattering coefficient are selected as the microwave signal sample information.Through appropriate training,the least squares support vector regression techniques are adopted to estimate soil moisture under different inversion schemes.The inversion results demonstrate high accuracy when multiple incident angles and the ratio of co-polarization backscattering coefficients are used as the microwave signal sample information.Comparison with the results of the artificial neural network(ANN)proved the validity and the anti-noise ability of the presented method,thus providing a new approach for the real-time retrieval of soil moisture.
small perturbation method(SPM);inversion of soil moisture;least squares support vector machine(LS-SVM)
O451;TN99
A
1005-0388(2015)02-0300-07

张清河(1969-),男,湖北人,三峡大学理学院副教授,博士,主要研究方向为电磁场数值计算、电磁散射与逆散射、天线理论与技术等.
徐 飞(1987-),女,湖北人,三峡大学理学院硕士研究生,主要研究方向为电磁散射与逆散射、微波对地遥感等.
邹启源(1988-),男,湖北人,三峡大学理学院硕士研究生,主要研究方向为粗糙面散射特性及埋地目标探测等.
张清河,徐 飞,邹启源.微扰法结合最小二乘支持向量机反演土壤湿度[J].电波科学学报,2015,30(2):300-306.
10.13443/j.cjors.2014051201
ZHANG Qinghe,XU Fei,ZOU Qiyuan.Inversion of bare soil moisture by the least squares support vector machine approach combined with SPM[J].Chinese Journal of Radio Science,2015,30(2):300-306.(in Chinese).doi:10.13443/j.cjors.2014051201
2014-05-12
国家自然科学基金项目(61179025);湖北省教育厅重点项目(D20111201)
联系人:张清河E-mail:zhangqh6973@163.com

