基于模糊相关机会规划的机会阵雷达方向图综合

龚树凤龙伟军，2潘明海贲 德，2

基于模糊相关机会规划的机会阵雷达方向图综合

龚树凤1龙伟军1，2潘明海1贲 德1，2

（1.南京航空航天大学雷达成像与微波光子技术教育部重点实验室，江苏南京210016；2.南京电子技术研究所，江苏南京210038）

研究了机会阵雷达的方向图综合问题，提出了一种基于模糊相关机会规划的方向图综合算法.该算法基于可信性理论，综合考虑天线单元分布的随机性以及工作状态的不确定性，以模糊变量来刻画天线单元参与方向图综合时的复杂不确定环境，建立方向图综合的规划模型.并结合模糊模拟算法和遗传算法设计了一种混合智能优化算法，用于求解该模型，仿真实验验证了所设计算法的有效性和稳定性.

机会阵雷达；方向图综合；可信性理论；相关机会规划；模糊模拟；遗传算法

引 言

机会阵雷达［1－3］是国外学者近年来针对新一代海军隐身驱逐舰DD（X）提出的一种新概念雷达，该雷达以平台隐身性为设计核心，以数字阵列雷达为基础，单元与数字收发组件可被任意布置于舰船的各个开放空间.机会阵雷达“机会性”地选择工作单元、工作方式及战术功能等.考虑到大量天线单元的任意随机分布，机会阵雷达方向图的综合与优化一直是国内外学者关注的重要课题［1－6］.在机会阵雷达的方向图综合中，如何合理地打开单元激励，尽量用最少的单元数目综合出满足条件的方向图，是一个十分重要的决策问题，属于组合优化中的NP－hard问题，可借助运筹学的目标优化理论求解.但现实世界中绝大多数优化问题或多或少含有不确定因素，在机会阵雷达的方向图综合中，工作单元的激励随机打开与关闭，最终能够合成所需方向图的天线单元数目是不确定的；即使天线数目确定，由于单元分布的随机性，最终综合出的方向图也会有所不同.因此，机会阵雷达的方向图综合是一个在不确定环境下的组合优化问题.目前，大量的文献对确定条件下的天线方向图综合算法进行了研究，归纳起来主要有以下几种算法：智能优化算法［7－9］、自适应算法［1011］和多次规划算法［12－13］等，但对含有不确定因素的方向图综合的研究还需进一步加强.

在含有不确定因素的组合优化中，不确定性不能简单地用随机性来刻画.事实上，很多情况下随机变量的概率密度函数是未知的，需要多次重复实验进行估计，但有些时候，无法进行这样的重复实验，在这种情况下，模糊变量不失为一个更好的选择.Zadeh［14］首先引入了模糊集的概念并用隶属度函数来刻画模糊现象.Zadeh为了测量一个模糊事件的需要提出了可能性测度的概念［15］.Liu等［16］提出了一种新的带有自对偶性的可信性的测度，简称为可信度.在2004年，Liu更是给出了可信性理论的公理化体系［17］.并结合此前的模糊规划［18］提出了模糊环境下的期望值模型、机会约束规划和相关机会规划模型［19－20］.近年来大量的研究已经表明，在模糊理论的研究领域中，可信性无论在理论上还是在应用上都起着重要的作用［21－23］.因此，本文将在可信性理论的基础上，运用模糊相关机会规划来实现机会阵雷达的方向图综合.文中以总数目一定且任意随机分布的阵列单元为环境，将整个阵列划分为多个区域，将方向图综合时每个区域内参与工作的单元数目均看作模糊变量，提出带有模糊参数的模糊相关机会规划模型；并结合模糊模拟算法和遗传算法设计了一种智能优化算法进行求解；最后通过具体的数值例子来验证算法的可行性和有效性.

1 模糊相关机会规划模型的建立

1.1基本概念

1965年，美国控制论学家Zadeh通过隶属函数首次提出了模糊集的概念.后来为了测量一个模糊事件的大小，Zadeh于1978年又提出了可能性测度的概念.在过去的几十年里，经过许多学者的共同努力，在模糊决策领域中可能性理论已经得到了广泛的发展和应用，但是后来人们却发现可能性测度不具备自对偶性.由于自对偶性在理论和应用中都扮演着重要的角色，Liu等提出了一个具备自对偶性的集函数，即可信度的测度概念.基于可信度，近几年来可信性理论得到了迅速的发展和广泛的研究.下面，先介绍可信性理论及其相关的一些基本概念.

定义1［16］设Θ是一个非空集合，P是Θ的幂集.如果集函数Cr满足下面条件：

（1）Cr｛Θ｝＝1；

（2）如果A⊂B，则Cr｛A｝≤Cr｛B｝；

（3）对于任意A∈P，有Cr｛A｝＋Cr｛AC｝＝1；

（4）对于P中的任意集族｛Ai｝，如果

则称Cr为可信度，此时，称三元组（Θ，P，Cr）为一个可信性空间.

定义2［17］模糊变量ξ是一个从可信性空间（Θ，P，Cr）到实数集R的函数.

定义3［17］如果ξ是定义在可信性空间（Θ，P，Cr）上的模糊变量，则它的隶属函数定义为

定理1［17］设ξ是一个模糊变量，其隶属函数为μ.对于任意Borel集合B，有

1.2问题的描述和模型的建立

在机会阵雷达方向图综合中，阵列单元随机任意分布，且工作状态的选择具有随机性.假设由N个各向同性辐射单元组成的随机分布阵列，阵元的空间位置为（xxi，yyi，zzi），i＝1，2，…，N，信号波长为λ，俯仰角为θ，方位角为φ，则阵列方向图为

式中：xi为阵元i的激励状态，1表示打开，0表示关闭；Ii为阵元i激励电流的幅度，默认为1；ψi为阵元i激励电流的相位，默认为0；τi（θ，φ）为阵元i相对参考点的时延，τi（θ，φ）＝（xxisinθcosφ＋yyisin θsinφ＋zzicosθ）／c，c为光速.

假设在阵元分布及总数目N确定的条件下进行方向图综合，优化的目标是极小化副瓣电平.由于阵元工作状态的随机性，最终参与方向图合成的单元数目是不确定的，随机抽取的单元数目小于N时就有可能综合出满足条件的方向图，所有阵元都工作时反而带来资源的浪费.在此用xi表示阵元i的工作状态，值为1表示激励打开，即阵元参与方向图综合；值为0表示激励关闭，阵元不参与方向图综合，因此有决策向量x＝［x1，x2，…，xN］，xi＝0或1.同时受阵元分布随机性的影响，同样数目的天线单元有多种分布状态，有多种组合形式，无法大量重复实验来取得其随机分布函数，此时，采用模糊变量来描述参与方向图综合的单元数目，同时将阵元分区进行分区处理.受模糊性的影响，认为在方向图综合时，参与的单元数目总和在一定程度上满足约束就可以了，综合的结果有些时候不能完全达到优化目标.在这种情况下，比较现实的办法是尽可能地达到优化目标，即最大化达成满足副瓣电平的机会.

本文以非均匀面阵为例，将其分为四个区域，每个区域内天线单元激励打开的数目分别为ξ1，ξ2，ξ3，ξ4，均为模糊变量.假设波束综合时天线单元激励打开的数目最大值为¯N，则有约束条件：

用f（x）表示方向图归一化后的最大副瓣电平，f（x）＝max（Lsbj），其中：Lsbj为第j个旁瓣电平，j＝1，2，…，J，J为旁瓣电平的数目.可以得到机会阵雷达方向图综合的模糊相关机会约束规划模型为

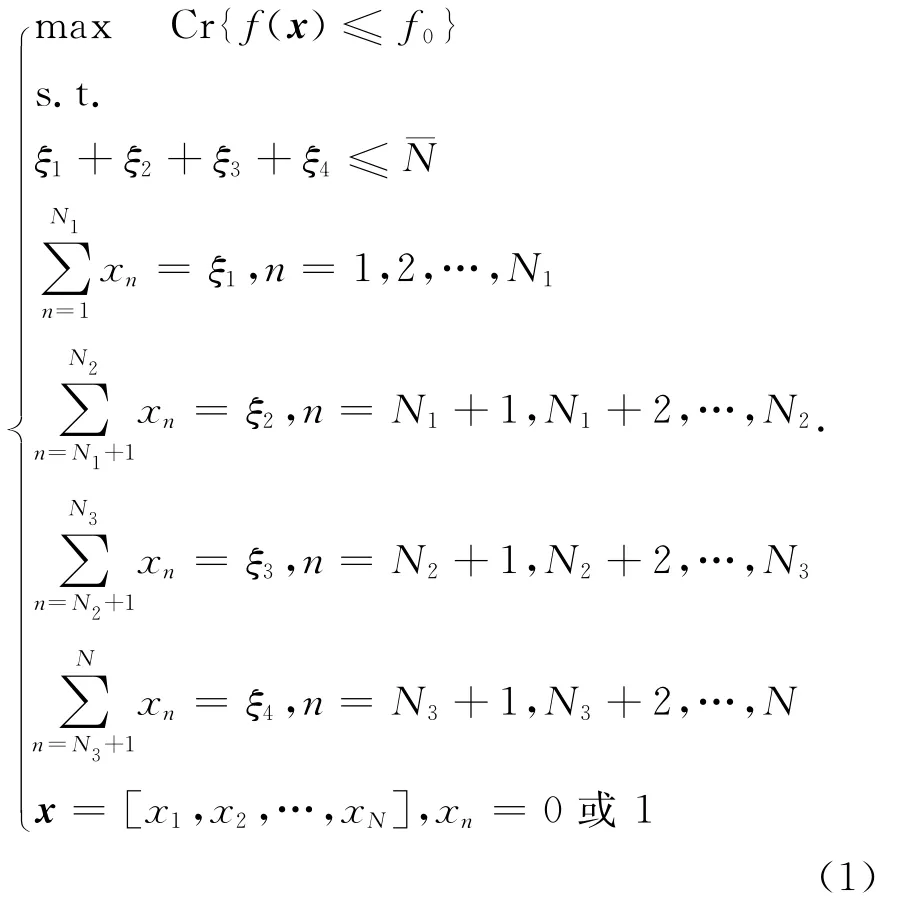
式中：Cr｛·｝表示事件｛·｝的可信度；x是决策向量；f0为预先给定的参考电平.那么模型的含义是在机会约束条件下，目标函数机会最大化.

2 模型求解算法

2.1模糊模拟

如何使用模糊模拟技术计算给定事件的机会函数.设E是模糊决策系统中的一个事件，又假设在点x处事件E的诱导约束为

y由点x导出，则事件E的机会函数为

若x∉E，可以立即得到l（x）＝0.对每一个固定的决策x∈E，首先置l（x）＝0，然后由模糊向量ξ随机生成一个清晰向量ξ0.实际上，对可能性较低的决策向量不感兴趣，所以，可以实现置一水平α0，然后从模糊向量ξ的α0水平截集中随机产生清晰向量ξ0.如果模糊向量ξ的α0水平截集过于复杂难于处理，可以从包含模糊向量ξ的α0水平截集的超几何体W中抽取向量，接受与否依赖于Cr｛ξ0｝＞α0是否成立.如果gj（y，ξ）≤0，j＝1，2，…，p及l（x）＜Cr｛ξ0｝，则置l（x）＝Cr｛ξ0｝，重复以上过程N次，则值l（x）可以作为它的估计值.具体步骤可以写为：

1）置l（x）＝0；

2）从模糊向量ξ的α0水平截集中随机产生清晰向量ξ0；

3）若gj（y，ξ）≤0，j＝1，2，…，p及l（x）≤Cr｛ξ0｝成立，则置l（x）＝Cr｛ξ0｝；

4）重复步骤2和3共N次；

5）返回l（x）.

在本文的方向图综合规划模型中，仅有一个事件f（x）≤f0，它的诱导约束为

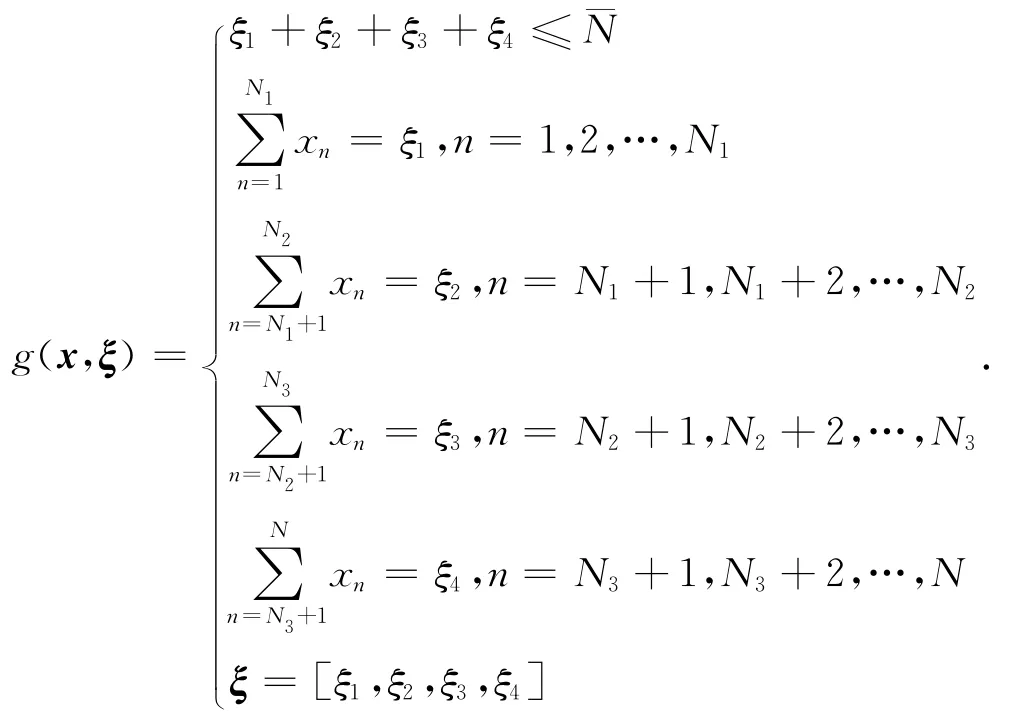
2.2混合智能优化算法

为了找到模糊相关机会约束规划模型的最优解，需要设计求解最优解的启发式优化算法.作为应用范围相当广泛的一种算法，遗传算法很适合作为求解工具［24－25］.将上一节设计的模糊模拟的方法嵌入到遗传算法中得到用来求解机会最大化模型的混合智能优化算法.算法的过程概括如下：

1）初始化输入参数：种群个数psize，交叉和变异概率pc，pm等，并产生psize个染色体，根据约束条件检验染色体的可行性；

2）通过交叉和变异操作更新染色体，并检验可行性；

3）使用模糊模拟计算所有染色体的目标值；

4）根据目标值使用基于序的评价函数计算每个染色体的适应度；

5）旋转赌轮盘选择染色体；

6）重复步骤2到步骤5直到给定的次数完成为止；

7）将最优染色体作为模型的最优解.

因此，本文事件的机会函数可以表示为

3 仿真实例

现假设一非均匀面阵，阵元随机分布在长宽均为10λ内的平面上，阵元总数目110，随机生成的阵元间距最小为0.05λ.按照天线单元的位置，将面阵划分为四个区域，与坐标平面内的象限区域划分一致，四个区域内的天线单元数目分别为44，15，18，33，如图1所示.

图1 天线单元优化前分布

假设波束综合时每个区域激励打开的天线单元数目均为梯形模糊变量，用ξ1，ξ2，ξ3，ξ4表示，其中：

ξ1（26，32，35，39），ξ2（4，8，11，14），

ξ3（7，10，13，17），ξ4（15，21，25，28）.

假设已知最大副瓣参考电平f0取值为－13.6 dB，综合时单元激励允许打开的最大数目¯N为85，基于此，模型（1）可以改写为

仿真时，程序中参数种群规模psize，交叉概率pc和变异概率pm等预先给定.通过赋予这些参数不同的数值，可以得到多组最优解和最优值.

天线单元分布图如图1所示时，共有110只天线单元.假设所有天线的激励幅度均为1，相位为0，则可以得到优化前的波束综合图，如图2所示，用G表示归一化方向图，最大副瓣电平－13.54dB，方向图图形表达中用U，V空间代替角度θ，φ，其中θ表示俯仰角，φ表示方位角，它们之间的关系为

U＝sinθcosφ，V＝sinθsinφ.

图2 优化前110只天线波束综合图

在程序中参数设置种群规模psize＝40，交叉概率pc＝0.8，变异概率pm＝0.1，迭代50次后，最大副瓣电平小于－13.6dB的机会为0.708，得到其中的一组最优解是优化后有71只天线单元工作，四个分区工作的单元数目为［29，6，13，23］，分布情况如图3所示.图3中的“＊”表示天线激励打开，“o”表示天线激励关闭.图4为优化后71只天线激励打开时的波束综合图，最大副瓣电平－14.06dB，比优化前有所提高，且工作天线单元数目变少节省了雷达资源.

改变程序中参数的设置，种群规模不变，交叉概率pc＝0.7，变异概率pm＝0.2，迭代50次后，仿真结果最大副瓣电平小于－13.6dB的机会为0.712，得到其中的一组最优解是优化后有78只天线单元工作，四个分区工作的单元数目为［32，12，13，21］，分布情况如图5所示.图5中的“＊”表示天线激励打开，“o”表示天线激励关闭.图6为优化后78只天线激励打开时的波束综合图，最大副瓣电平－14.6 dB，比优化前提高了1dB，且工作天线单元数目节省了32只.

图3 优化后71只天线单元分布

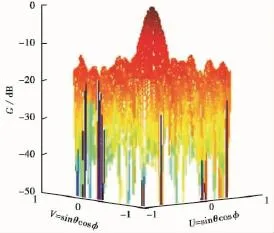
图4 优化后71只天线波束综合图

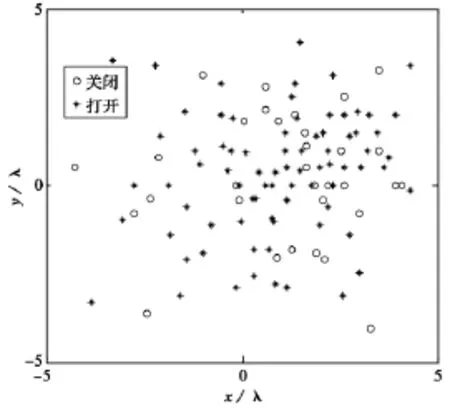
图5 优化后78只天线单元分布

图6 优化后78只天线单元波束综合图

表1给出了不同参数设置下的机会最大化模型结果比较.由表中数据可以看出，不同参数设置下，最终得到的可信度均在0.7左右，说明算法是稳定和有效的.

表1 机会最大化模型结果比较

4 结 论

本文针对不确定环境下的机会阵波束综合问题进行了研究.机会阵阵元任意分布，波束综合时工作状态不确定，同时为节省天线资源，对最终参与工作的天线单元数目进行约束，提出了一种基于模糊相关机会规划的方向图综合算法.在综合时，给定约束条件，将随机参与方向图综合的天线单元数目看作模糊变量建立相关机会规划模型，并结合模糊模拟技术和遗传算法设计了一种新的混合智能优化算法对其进行优化求解.最后，仿真结果表明了在不确定环境条件的约束下，最大副瓣电平满足条件的机会为0.7左右，且不同参数的结果表明算法是稳定和有效的.本文方法也可用于任意阵阵元的布局，对工程实践有一定的指导意义.

［1］ JON A B.Genetic Algorithms As A Tool For Opportunistic Phased Array Radar Design［D］.Monterey：Naval Postgraduate School，2002.

［2］ LANCE C E.Genetic Algorithm Design and Testing of A Random Element 3－D 2.4GHz Phased Array Transmit Antenna Constructed of Commercial RF Microchips［D］.Monterey：Naval Postgraduate School，2003.

［3］ IBRAHIM K.Distributed Beam Forming in A Swarm UAV Network［D］.Monterey：Naval Postgraduate School，2008.

［4］ LONG W J，BEN D，PAN M H.Pattern synthesis for OAR using LSFE－GA method［J］.International Journal of RF and Microwave Computer－aided Engineering，2011，21（5）：584－588.

［5］ 龙伟军，贲 德，BAKHSHI A D，等.三维机会阵雷达波束综合优化［J］.电波科学学报，2010，25（1）：93－98.

LONG Weijun，BEN De，BAKHSHI A D，et al.Pattern synthesis optimization of 3－D oppportunistic array radar［J］.Chinese Journal of Radio Science，2010，25（1）：93－98.（in Chinese）

［6］ 龚树凤，贲 德，潘明海，等.一种考虑互耦的机会阵雷达波束综合方法［J］.电波科学学报，2014，29（1）：12－18.

GONG Shufeng，BEN De，PAN Minghai，et al.A novel method for pattern synthesis of opportunistic array radar with mutual coupling［J］.Chinese Journal of Radio Science，2014，29（1）：12－18.（in Chinese）

［7］ LING C，ZHU L Y，WEE S.Linear aperiodic array synthesis using an improved genetic algorithm［J］.IEEE Transactions on Antennas and Propagation，2012，60（2）：895－892.

［8］ WANG W B，FENG Q Y，LIU D.Application of chaotic particle swarm optimization algorithm to pattern synthesis of antenna arrays［J］.Progress in Electromagnetics Research，2011，115：173－189.

［9］ RANDY L P.Thinned arrays using genetic algorithms［J］.IEEE Transactions on Antennas and Propagation，1994，42（7）：993－999.

［10］ OLEN C A，COMPTON R T.A numerical pattern synthesis algorithm for arrays［J］.IEEE Transaction on Antenna and Propagation，1990，38（10）：1666－1676.

［11］ ZHOU P Y，INGRAM M A.Pattern synthesis for arbitrary arrays using an adaptive array method［J］.IEEE Transaction on Antenna and Propagation，1998，46（11）：1759－1760.

［12］ ZHAN S，ZHENGHE F.A new array pattern synthesis algorithm using the two－step least－squares method［J］.IEEE Signal Processing Letters，2005，12（3）：250－253.

［13］ YAN S F，MA Y L，SUN C.Optimal beamforming for arbitrary arrays using second－order cone programming［J］.Chinese Journal of Acoustics，2005，24（1）：1－9.

［14］ ZADEH L A.Fuzzy sets［J］.Information and Control，1965，8：338－353.

［15］ ZADEH L A.Fuzzy sets as a basis for a theory of possibility［J］.Fuzzy Sets and Systems，1999，100（S1）：9－34.

［16］ LIU B D，LIU Y K.Expected value of fuzzy variable and fuzzy expected value models［J］.IEEE Transaction on Fuzzy Systems，2002，10：445－450.

［17］ LIU B D.Uncertainty Theory：An Introduction to Its Axiomatic Foundations［M］.Berlin：Spring－Verlag，2004：109－128.

［18］ 刘宝碇，赵瑞清.随机规划与模糊规划［M］.北京：清华大学出版社，1998：164－183.

［19］ LIU B D.Fuzzy random chance－constrained programming［J］.IEEE Transaction on Fuzzy Systems，2001，9（5）：713－720.

［20］ LIU B D.Fuzzy random depent－chance programming［J］.IEEE Transaction on Fuzzy Systems，2001，9（5）：721－726.

［21］ 陈根宗，刘湘伟，雄 杰.模糊机会约束规划在雷达干扰资优化分配中的应用［J］.现代防御技术，2010，38（6）：128－133.

CHEN Gengzong，LIU Xiangwei，XIONG Jie.Application of fuzzy chance constrained programming in optimal distribution of radar jamming resource［J］.Modern Defence Technology，2010，38（6）：128－133.

［22］ 吴杰康，唐 力.基于模糊机会约束规划的水火电力系统多目标随机调度模型［J］.中国电机工程学报，2011，31（25）：26－34.

WU Jiekang，TANG Li.Multi－objective stochastic scheduling models for hydrothermal plants on fuzzy chance constrained programming［J］.Proceedings of the CSEE，2011，31（25）：26－34.（in Chinese）

［23］ ZHAO T，WANG X.A fuzzy chance－constrained programming model for liquid chlorine downstream products selection problem in environmental services［C］／／2011Annual SRII Global Conference.San Jose，2011：630－635.

［24］ 王丽娜，王 兵，周贤伟.一种新的智能天线波束形成算法［J］.电波科学学报，2007，22（2）：351－354.

WANG Lina，WANG Bing，ZHOU Xianwei.A novel beamforming algorithm of smart antenna［J］.Chinese Journal of Radio Sciencs，2007，22（2）：351－354.（in Chinese）

［25］ 赵福玲，王永军，何少林，等.遗传算法综合智能天线的赋形波束［J］.电波科学学报，2011，26（3）：593－597.

ZHAO Fuling，WANG Yongjun，HE Shaolin，et al.Shape beam of smart antenna synthesized by genetic algorithm［J］.Chinese Journal of Radio Sciencs，2011，26（3）：593－597.（in Chinese）

Pattern synthesis for opportunistic array radar based on fuzzy dependent－chance programming

GONG Shufeng1LONG Weijun1，2PAN Minghai1BEN De1，2
（1.Key Laboratory of Radar Imaging and Microwave Photonics，Nanjing Univ Aeronaut Astronaut，Ministry of Education，Nanjing University of Aeronautics and Astronautics，Nanjing Jiangsu 210016，China；2.Nanjing Research Institute of Electronics Technology，Nanjing Jiangsu 210038，China）

In this paper，the problem of pattern synthesis for opportunistic array radar is studied，and a new pattern synthesis algorithm based on fuzzy dependent－chance programming is proposed.The algorithm based on credibility theory，considers antenna elements with random distribution and excited state of uncertainty，uses fuzzy variables to characterize the complex and uncertain environment of antenna elements，and creates the programming model for pattern synthesis.A searching method integrating the technique of fuzzy simulation and genetic algorithm is designed to search the quasi－optimal schedule under some decision－making criterion.Simulation examples are given to demonstrate the feasibility of the searching method for solving the proposed model.

opportunistic array radar；pattern synthesis；credibility theory；dependentchance programming；fuzzy simulation；genetic algorithms

TN911.7

A

1005－0388（2015）02－0201－07

龚树凤（1985－），女，河北人，南京航空航天大学电子信息工程学院在读博士研究生，主要研究方向为新体制雷达、雷达信号处理等.

龙伟军（1978－），男，云南人，博士，目前就职于南京电子技术研究所，研究方向为新体制雷达、阵列波束综合、雷达信息处理和信号传输.

潘明海（1962－），男，河北人，南京航空航天大学电子信息工程学院教授，博士生导师，主要研究方向为新体制雷达、射频仿真以及雷达信号处理.

贲 德（1938－），男，吉林人，中国工程院院士，南京航空航天大学电子信息工程学院院长，教授，博士生导师，就职于南京电子技术研究所，主要研究方向为新体制雷达、雷达信号处理等.

龚树凤，龙伟军，潘明海，等.基于模糊相关机会规划的机会阵雷达方向图综合［J］.电波科学学报，2015，30（2）：201－207.

10.13443／j.cjors.2014051901

GONG Shufeng，LONG Weijun，PAN Minghai，et al.Pattern synthesis for opportunistic array radar based on fuzzy dependent－chance programming［J］.Chinese Journal of Radio Science，2015，30（2）：201－207.（in Chinese）.doi：10.13443／j.cjors.2014051901

2014－05－19

国家自然科学基金（No.61071164、61271327）；江苏高校优势学科建设工程项目

联系人：龚树凤E－mail：suffy＿nuaa＠163.com