L波段小擦地角海杂波幅度均值与风速关系建模

张玉石许心瑜吴振森黎 鑫

L波段小擦地角海杂波幅度均值与风速关系建模

张玉石1，2许心瑜2吴振森1黎 鑫2

（1.西安电子科技大学物理与光电工程学院，陕西西安710071；2.中国电波传播研究所，山东青岛266107）

在对比分析国际上现有模型中风速对海杂波幅度均值的影响基础上，提出了一种新的两分量高斯模型建立海杂波幅度均值与风速的关系.结合我国黄海L波段VV极化小擦地角海杂波实测数据，对该模型进行了验证与精度分析，并研究了该模型参数随擦地角的变化关系，给出了模型拟合参数.从数据分析的结果来看，该模型较好地捕获了海杂波幅度随风速的变化趋势，可为雷达系统设计和雷达海杂波预测提供技术支撑.

雷达；海杂波；小擦地角；幅度均值

引 言

下视雷达要实现远距离海上目标或海面低空飞行目标的有效检测，海面引起的雷达后向散射回波（称为海杂波）的影响不容忽视.近年来，小擦地角海杂波特性研究受到了广泛关注，国内外学者开展了大量小擦地角海杂波数据分析与建模等研究，主要包括海杂波幅度统计特性、多普勒谱特性、时间与空间相关特性以及非线性特性等［1－10］.海杂波幅度统计建模又包括幅度均值（或均值散射系数）建模和幅度统计分布建模.目前国际上已经建立了多个小擦地角海杂波的幅度均值模型，如乔治亚理工学院（Georgia Institute of Technology，GIT）模型、混合（Hybrid，HYB）模型、TSC技术服务公司（Technology Service Corporation，TSC）模型、Sittrop（SIT）模型、海军实验室（Naval Research Laboratory，NRL）模型等［11－13］，并且有部分学者结合实测数据研究了海杂波幅度均值特性及部分模型的适用性.20世纪90年代Chan H.C.［14］利用工作在高频（Very High Frequency，VHF）、特高频（Ultra High Frequency，UHF）、L、S和X波段的雷达获取的小擦地角海杂波数据，进行了详细分析，结果表明实测海杂波幅度均值在较低海况下与GIT、SIT模型结果存在差异；Dong等人［15］利用L波段多通道雷达获取的小擦地角海杂波数据，分析结果表明海杂波幅度均值随擦地角的变化与典型模型结果明显存在不一致性.Zhang等人［16］的研究表明近海海域L波段海杂波实测幅度均值结果与典型模型存在较大差异.

如上所述，现有模型的差异较大，普适性不强.而如何准确定量地建立雷达参数、海洋环境参数与海杂波幅度均值之间的关系仍是个难题，目前还缺乏适合于我国东南沿海的模型.因此，通过海杂波特性与风速关系的研究，给出随风速变化的海杂波幅度均值变化趋势，可为雷达系统设计和雷达海杂波预测提供技术依据.

海杂波幅度均值与风速的关系，除上述模型外，仅有部分中等擦地角下结果，如Wetzel，L.B.［17］给出了海杂波随风速变化的幂函数关系；Sarkar A.等人［18］给出了L波段海杂波随风速变化的多项式模型及相关的参数.目前小擦地角海杂波特性研究大多集中在较高的频率（如X波段），而针对L波段的研究较少［14－15］，特别是海杂波与海洋环境参数（如风速、波高等）定量关系的建立.为此，本文对现有模型中海杂波幅度均值与风速关系进行了修正，提出了一种两分量高斯模型，结合L波段VV极化小擦地角海杂波实测数据，验证了该模型的有效性，并研究了该模型参数与擦地角之间的关系，给出了参数变化的经验公式和拟合结果.

1 模型对比分析

1.1风速对海杂波幅度均值的影响分析

风是引起海面状态变化的最主要因素，不同的风速和风向引起海面的起伏特性也不同，海表面形貌与风速及有效波高的关系可用海况等级进行描述［17］.GIT和TSC模型建立了风速因子来描述风速的影响，而HYB和NRL模型则采用海况等级作为输入参数.从这些模型的形式和输入参数之间的关系来看，存在一定的差异［3］，如风速与海况的关系在NRL模型和GIT模型中采用了如下不同的系数：

式中：Vw为风速，m／s；S为道格拉斯海况等级.

从式（1）、（2）可以看出，在同样风速情况下海况等级在两种模型下甚至超过了1级，而在同等海况下，特别是高海况下风速的差别甚至超过了3m／s.

VV极化海杂波幅度均值的GIT模型为

式中：λ为波长，m；φ为擦地角，rad；ha为平均波高，m；Gm为干涉因子；Gu为风向因子；Gw为风速因子.

为了便于在模型之间比较风速对海杂波幅度均值的影响，引入幅度因子的概念，即令模型中与波高和风向有关的项为常数，排除波高和风向的影响，仅考虑风速对幅度均值的影响趋势.如令风向因子和干涉因子为1，令1.73ln（ha＋0.015）为0，并将L波段的波长值带入公式（3），则可得出与擦地角和风速有关的幅度因子

VV极化海杂波幅度均值的TSC模型为

式中：λ为波长，m；φ为擦地角，rad；σz为海面高度标准差，m；GA为小擦地角因子.

类似地，将L波段波长值带入公式（5），可以得出TSC模型中与波长、擦地角和风速有关的幅度因子

从公式（4）和（6）可以看出，两个模型中幅度因子的形式比较相近，主要差别在于对数函数中指数的变化系数和形式.在擦地角1°～5°情况下，两种模型中幅度因子对比分析结果如图1所示.可以看出：在GIT模型中，随风速增大，变化趋势较缓，逐渐趋于饱和，并且在较小的风速值时，幅度值随风速减小下降较快；而在TSC模型中，随风速增大上升趋势较明显，且未呈现趋于饱和的趋势.

图1 GIT和TSC模型中风速的影响对比分析

NRL和HYB模型均是以海况等级作为输入参数，并且NRL模型是大量不同风向下数据的平均结果，没有风向因子.为便于多个模型之间进行对比分析，采用模型给出的风速、波高与海况关系，将空间应用中心（Space Applications Centre，SAC）模型［18］应用于小擦地角条件下.由于其他风向结果类似，仅给出3°擦地角逆风向条件下的对比结果，如图2所示.可以看出NRL模型和TSC模型的趋势最接近，HYB模型的上升趋势最明显，GIT模型在较低风速情况下趋势明显与其他几个模型不一致，SAC模型的散射系数值明显偏大，小擦地角条件下的适用性较差.本文后面将提出的两分量高斯模型在较大风速情况下与HYB模型接近，在较小风速情况下介于TSC与SAC模型之间.

1.2海杂波幅度均值的两分量高斯模型

在已有模型对比分析基础上，结合不同海况下该频段实测海杂波幅度均值特性［19－20］，并考虑到近海海域的海浪特点，进一步比较其他几种典型的模型，如高斯模型、指数模型、幂函数、多项式等，优选出较为适合的高斯函数作为基函数，提出两分量高斯模型对风速与海杂波幅度均值关系进行建模，其模型表达式如下：

图2 多个海杂波幅度均值模型对比分析

式中：A1，A2，C1，C2，W1，W2为模型系数.该模型表现为两个高斯函数的和形式，调整第一个高斯函数的幅度参数A1、中心C1和形状系数W1，可实现对海杂波幅度均值的整体强度、中低风速下的幅度起伏中心和形状的调整.第二个高斯函数中的参数体现为较高风速下杂波幅度起伏中心、形状的变化以及幅度在第一个高斯函数基础上的微变化.

2 数据分析与模型验证

2.1数据描述与分析

本文采用的实测数据是由中国电波传播研究所的岸基海杂波观测雷达录取［16］.该雷达架设于青岛市海拔100m的岸基平台上，面向方位201°观测黄海海域的海面杂波.雷达工作于L波段，观测的擦地角范围为1.5°～6.5°.本文共选取了2008年测试的212组实测VV极化数据.数据对应的擦地角范围为2.7°～4.8°.图3给出了与实测数据同步记录的有效波高、风速、风向和波向（风向和波向为相对雷达波束的指向角度）结果.从图中可以看出，最大波高为1.6m，最大风速为11.1m／s，最大海况达到了4～5级.通过四个海洋环境参数的对比，可以看出某些情况下波向与风向存在差异，且在有些情况下较大风速并没有产生较高的波高（如图中①区域），而较低风速也可能产生较高的波高（如图中②区域），这表明有些数据是由非平稳海面情况下记录的.同时在相对较高的波高情况下，大部分数据下风速和波高的关系趋势及风向与波向的大体一致性还是较为明显的（如图中③～⑥区域）.因此，选取的实测数据体现了兼有充分发展和非充分发展海表面下的测试结果.

不同擦地角下实测海杂波幅度均值随风速的变化如图4所示，可以看出随着擦地角减小，海杂波幅度均值呈下降的趋势.随着风速的增加，在中等风速以下呈震荡趋势，当风速大于9m／s时，出现较大增幅.这与图2中各典型模型随风速变化的趋势存在较明显的差别.对照图3可以看出，在中等风速以下，海浪波高的变化较大且与风速的关系存在不确定性，这可能是导致散射系数随风速起伏变化的一个主要原因.

图3 同步记录的海洋环境参数

图4 不同擦地角下实测海杂波幅度均值随风速变化

2.2模型验证分析

图5给出了擦地角2.7°情况下实测杂波数据与两分量高斯模型拟合的结果.多个角度下实测数据采用该模型拟合后的均方根误差和残数的标准偏差如图6所示.可以看出误差在2dB以下，获得了较好的匹配效果.

通过非线性最优化拟合方法，进一步给出了模型各个参数随擦地角的变化，如图7所示.从结果可以看出系数A1和A2随擦地角变化较大，其他模型系数随擦地角变化较小.

图8给出了对参数A1和A2随擦地角变化进行二次拟合，其他参数采用不同擦地角下平均值的效果对比.从与实际结果对比可以看出，对两个参数进行拟合后的总体偏差小于0.2dB，中等风速以下拟合效果较好，仅在较大风速下拟合效果稍差.由此可见，在两分量高斯模型中引入擦地角的变化影响，仅需调整高斯分量中的两个幅度参数与擦地角的关系即可达到较高的模型精度.

图5 擦地角2.7°时实测海杂波数据的模型验证结果

图6 不同擦地角下两分量高斯模型拟合误差分析

图7 两分量高斯模型参数随擦地角变化关系

参数A1和A2随擦地角变化的拟合结果及不同擦地角下的残数结果如图9所示，通过二次拟合后的残数可控制在0.1dB以下.A1随擦地角的变化采用如下二阶指数函数拟合

式中：θ为擦地角，度；a1、a2、κ1、κ2为函数系数.

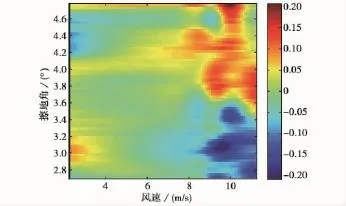
图8 参数A1和A2随擦地角关系拟合与实际效果对比

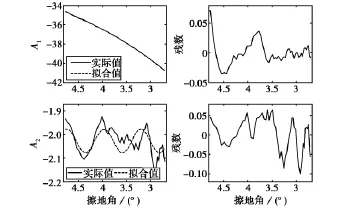
图9 参数A1和A2随擦地角变化与模型比较

A2随擦地角的变化采用如下函数进行拟合：

式中，a3、a4、a5、κ3为函数系数.

如上所述，小擦地角海杂波幅度均值与风速的变化关系可通过两分量高斯模型表述，其中高斯分量的幅度参数与擦地角变化的关系可通过公式（8）和公式（9）的函数进行描述，其中的参数估计采用最小二乘方法.L波段VV极化实测海杂波数据的模型验证拟合分析表明，该模型与实测数据的吻合度较高.根据实测数据拟合得到的模型参数如表1所示.

表1 实测数据分析获得的模型参数

3 讨论与结论

本文在分析风速对小擦地角海杂波幅度均值影响基础上，提出了两分量高斯模型描述风速与海杂波幅度均值之间的关系，利用L波段VV极化小擦地角实测海杂波数据对模型进行了验证.从分析结果来看，海杂波幅度均值随风速的变化趋势可通过该模型获得较好的匹配效果.在此基础上，提出采用二阶指数函数和傅里叶函数分别建立两个高斯分量的幅度参数与擦地角之间的变化关系，并给出了拟合的残数结果.结果表明，采用两分量高斯模型建立海杂波幅度均值与风速的关系，在小擦地角下能够获得较高的建模精度.

致谢：感谢中国电波传播研究所第二研究部杂波课题组全体同志为数据获取实验付出的努力.

［1］ WARD K D，BAKER C J，WATTS S.Maritime surveillance radar part I：radar scattering from the ocean surface［J］.IEE Proceedings Part F，Radar Signal Processing，1990，137（2）：51－62.

［2］ WALKER D.Experimentally motivated model for low grazing angle radar Doppler spectra of the sea surface［J］.IEE Proceedings Radar，Sonar and Navigation，2000，147（3）：114－120.

［3］ LEONARD T P，ANTIPOV I，WARD K.D.A comparison of radar sea clutter models［C］／／IEEE International Radar Conference.Long Beach，2002：429－433.

［4］ GRECO M，GINI F，RANGASWAMY M.Statistical analysis of measured polarimetric clutter data at different range resolutions［J］.IEE Proceedings Radar Sonar and Navigation，2006，153（6）：473－481.

［5］ 关 键，丁 昊，黄 勇，等.实测海杂波数据空间相关性研究［J］.电波科学学报，2012，27（5）：943－953.

GUAN Jian，DING Hao，HUANG Yong，et al.Spatial correlation property with measured sea clutter data［J］.Chinese Journal of Radio Science，2012，27（5）：943－953.（in Chinese）

［6］ 吴振森，衣方磊.一维动态海面的电磁散射杂波模拟和参数估计［J］.电波科学学报，2003，18（2）：132－137.

WU Zhensen，YI Fanglei.Numerical simulation and parameters estimation of scattering clutter from 1－D time－varying sea surface［J］.Chinese Journal of Radio Science，2003，18（2）：132－137.（in Chinese）

［7］ 刘宁波，关 键，黄 勇，等.海杂波的分段分数布朗运动模型［J］.物理学报，2012，61（19）：190503.

LIU Ningbo，GUAN Jian，HUANG Yong，et al.Piecewise fractional Brownian motion for modeling sea clutter［J］.Acta Physica Sinica，2012，61（19）：190503.（in Chinese）

［8］ ANTIPOV I.Analysis of Sea Clutter Data［R］.Defence Science and Technology Organisation，1998.

［9］ WARD K D，TOUGH R J A，WATTS S.Sea Clutter：Scattering，the K－distribution and Radar Performance［M］.London：The Institution of Engineering and Technology，2006.

［10］ NATHANSON F E，REILLY J P，COHEN M N.Radar Design Principles［M］.2nd ed.New York：McGraw－Hill，1991.

［11］ ANTIPOV I.Simulation of Sea Clutter Returns［R］.Defence Science and Technology Organisation，1998.

［12］ SPAULDING B，HORTON D，PHAM H.Wind aspect factor in sea clutter modeling［C］／／IEEE International Radar Conference.Arlington，May 9－12，2005：89－9.

［13］ GREGERS－HANSEN V，MITAL R.An empirical sea clutter model for low grazing angles［C］／／IEEE International Radar Conference.Pasedena，May 4－8，2009：1－5.

［14］ CHAN H C.Radar sea－clutter at low grazing angles［J］.IEE Proceedings Part F，Radar Signal Processing，1990，137（2）：102－112.

［15］ DONG Y，MERRETT D.Analysis of L－band multichannel sea clutter［J］.IET Radar，Sonar and Navigation，2010，4（2）：223－238.

［16］ ZHANG Yushi，WU Zhensen，ZHANG Zhedong，et al.Applicability of sea clutter models in nonequilibrium sea conditions［C］／／IET International Radar Conference，Guilin，2009.

［17］ SKOLNIK M I.Radar Handbook［M］.3nd ed.New York：McGraw－Hill，2008.

［18］ SARKAR A，BHANDURI L，KUMAR R.Wind dependence of L－Band radar backscatter［J］.Defense Science Journal，1985，35（4）：383－389.

［19］ 张玉石，张忠治，李善斌，等.高分辨率海杂波观测研究［J］.电波科学学报，2008，23（6）：1119－1122.

ZHANG Yushi，ZHANG Zhongzhi，LI Shanbin，et al.Measurement of high resolution sea clutter［J］.Chinese Journal of Radio Science，2008，23（6）：1119－1122.（in Chinese）

［20］ 张玉石，吴振森，李善斌.高海况下小擦地角海杂波特性研究［C］／／第十届电波年会，武汉，2009.

Modeling windspeed behavior of L－band sea clutter average reflectivity at low grazing angles

ZHANG Yushi1，2XU Xinyu2WU Zhensen1LI Xin2
（1.School of Physics Optoelectronic Engineering，Xidian Universty，Xi’an Shaanxi 710071，China；2.Chinese Research Institute of Radiowave Propagation，Qingdao Shandong266071，China）

A new tow－component Gaussian model is presented on the basis of the comparative analysis of the impact of wind speed on sea clutter average reflectivity described by existing international models.Based on the measured sea clutter data of VV polarization at low grazing angles collected by a L－band radar at the yellow sea of china，the model was validated with precision analysis.The relationship between the model parameters and grazing angle is analyzed and the fitting parameters of the model is given.According to the results of data analysis，the proposed model can well capture the trend of the sea clutter amplitude with wind speed.This model is important for design of radar systems and radar sea clutter prediction.

radar；sea clutter；low grazing angle；average reflectivity

P412.25

A

1005－0388（2015）02－0289－06

张玉石（1978－），男，辽宁人，西安电子科技大学博士研究生，中国电波传播研究所高级工程师，主要从事地海杂波测试系统与方法、地海杂波特性与建模等研究.

许心瑜（1982－），女，河南人，硕士研究生，工程师，主要从事地海杂波数据处理及特性研究.

吴振森（1946－），男，湖北人，教授，博士生导师，研究方向为随机介质、非均匀介质中电磁（光）波的传播与散射、目标激光散射特性和电磁散射等方面.

黎 鑫 （1983－），男，安徽人，硕士研究生，工程师，主要从事地海杂波测试、数据分析与建模研究.

张玉石，许心瑜，吴振森，等.L波段小擦地角海杂波幅度均值与风速关系建模［J］.电波科学学报，2015，30（2）：289－294.

10.13443／j.cjors.2014042001

ZHANG Yushi，XU Xinyu，WU Zhensen，et al.Modeling windspeed behavior of L－band sea clutter average reflectivity at low grazing angles［J］.Chinese Journal of Radio Science，2015，30（2）：289－294.（in Chinese）.doi：10.13443／j.cjors.2014042001

2014－04－20

联系人：张玉石E－mail：zhang10695＠126.com