Hom-L-dendriform代数与Hom-L-quadri代数

安慧辉, 王治淳, 薛 晨

Hom-L-dendriform代数与Hom-L-quadri代数

安慧辉, 王治淳, 薛 晨

(辽宁师范大学数学学院,辽宁大连 116029)

Hom-L-dendriform代数和Hom-L-quadri代数分别是由L-dendriform代数和L-quadri代数通过代数形变得出的。引入Hom-L-dendriform代数和Hom-L-quadri代数的定义,给出了利用L-dendriform代数以及L-dendriform代数上的代数同态构造Hom-L-dendriform代数的方法,同时给出利用L-quadri代数以及L-quadri代数上的代数同态构造Hom-L-quadri代数的方法,最后给出Hom-pre-Lie代数、Hom-L-dendriform代数和Hom-L-quadri代数之间的关系。

Hom-pre-Lie代数;Hom-L-dendriform代数;Hom-L-quadri代数

0 引 言

Dendriform代数是一类重要的Loday代数[1],Quadri代数是由Aguiar和Loday引入的,也是一类常见的Loday代数。Loday代数的种类有很多,例如NS代数[2]、octo代数、dendriform-Nijenhuis代数[2]等。概括来说,Loday代数是一系列具有“分裂结合性”的代数,与Lie代数、组合学、量子场论和同调论等领域密切相关,近年来的发展极为迅速,已被广泛而深入地研究。L-dendriform代数[3]可以看作是dendriform代数的Lie代数类似结构,L-quadri代数则可以看作是Quadri代数的Lie代数类似结构。Lie代数是由结合代数的换位运算给出的,pre-Lie代数[4]是由dendriform代数的某种换位运算给出的。同样的,L-dendriform代数也可以给出pre-Lie代数结构。结合代数、Dendriform代数与Quadri代数存在如下关系:

结合代数←Dendriform代数←Quadri代数

类似的,Lie代数、pre-Lie代数、L-dendriform代数与L-quadri代数有如下关系:

Lie代数←Pre-Lie代数←L-dendriform代数

←L-quadri代数

本文先介绍了Hom-L-dendriform代数的定义,研究了Hom-L-dendriform代数与L-dendriform代数之间的关系,以及Hom-L-dendriform代数与Hom-pre-Lie代数、Hom-Lie代数之间的关系。然后介绍了Hom-L-quadri代数的定义,给出了Hom-L-quadri代数与L-quadri代数之间的关系,以及Hom-pre-Lie代数、Hom-L-dendriform代数以及Hom-L-quadri代数之间的关系。

1 基本结论

定义1.1[5]假设A是一个线性空间,[,]是A上的代数运算,且[,]是双线性的,α:A→A是代数同态,若∀x,y,z∈A,有

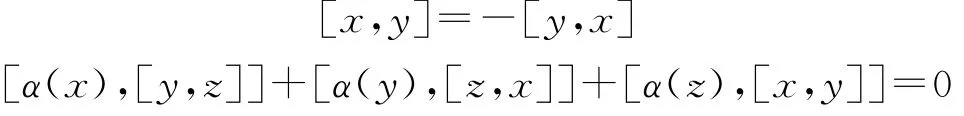
则称(A,[,],α)是Hom-Lie代数。

定义1.2[4]假设A是一个线性空间,◦是A上的代数运算,且◦是双线性的,若∀x,y,z∈A,

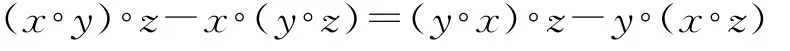
则称(A,◦)是pre-Lie代数。

定义1.3[5]假设A是一个线性空间,◦是A上的代数运算,且◦是双线性的,α:A→A是代数同态,若∀x,y,z∈A,有

则称(A,◦,α)是Hom-pre-Lie代数。

命题1.1[5]设(A,◦,α)是Hom-pre-Lie代数,定义

则(A,[,],α)是一个Hom-Lie代数,称为A的相关Hom-Lie代数,记作g(A)。

定义1.4[3]假设A是一个线性空间,▷,◁是2个A⊗A→A上的双线性运算,如果对∀x,y,z∈A,满足

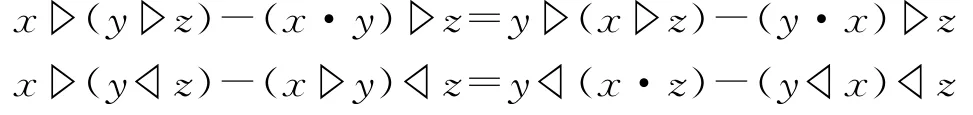
其中

则称(A,▷,◁)为L-dendriform代数。

定义1.5[6]假设A是一个线性空间,↘,↗,↖,↙是4个A⊗A→A上的双线性运算,如果对∀x,y,z∈A满足

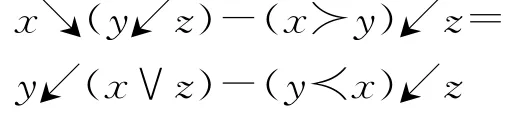
其中

则称(A,↘,↗,↖,↙)为L-quadri代数。

2 Hom-L-dendriform代数

定义2.1假设A是一个线性空间,▷,◁是2个A⊗A→A的双线性运算,α:A→A是代数同态,如果对∀x,y,z∈A满足

其中

则称(A,▷,◁,α)为Hom-L-dendriform代数。

命题2.1假设(A,▷,◁)是L-dendriform代数,α:A→A是代数同态,令α◦▷=▷α,α◦◁=◁α,则(A,▷α,◁α,α)是Hom-L-dendriform代数。

证令α◦·=·α,由已知

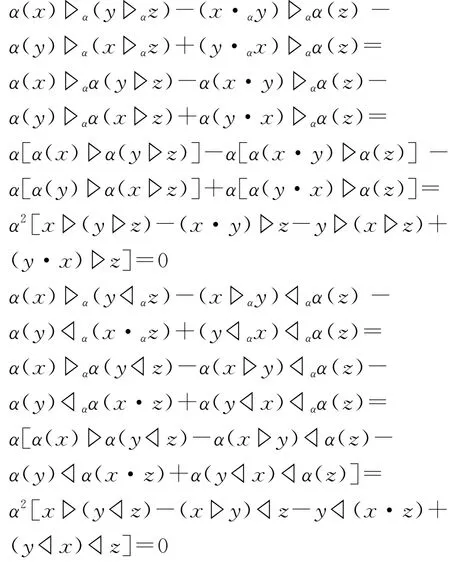
因此,(A,▷α,◁α,α)是Hom-L-dendriform代数。

命题2.2假设(A,▷,◁,α)为Hom-L-dendriform代数,

(1)如果定义

则(A,≥,α)是一个Hom-pre-Lie代数,称(A,≥, α)为(A,▷,◁,α)的相关水平Hom-pre-Lie代数。

(2)如果定义

则(A,≤,α)是一个Hom-pre-Lie代数,称(A,≤, α)为(A,▷,◁,α)的相关垂直Hom-pre-Lie代数。

(3)(A,▷,◁,α)的相关垂直与水平Hompre-Lie代数(A,≤,α)和(A,≥,α)有共同的Hom-Lie代数g(A),括积运算为

[x,y]=x▷y+x◁y-y▷x-y◁x,∀x,y∈A,称此Hom-Lie代数为(A,▷,◁,α)的相关Hom-Lie代数。

证由于(1),(2)的证明相似,因此只给出(1)的证明。

由Hom-L-dendriform代数定义,可以得到

所以,(A,≥,α)是一个Hom-pre-Lie代数。

由(1),(2)以及“命题1.1”即可推出(3)。

3 Hom-L-quadri代数

定义3.1假设A是一个线性空间,↘,↗,↖,↙是4个A⊗A→A上的双线性运算,α:A→A是代数同态,如果对∀x,y,z∈A满足

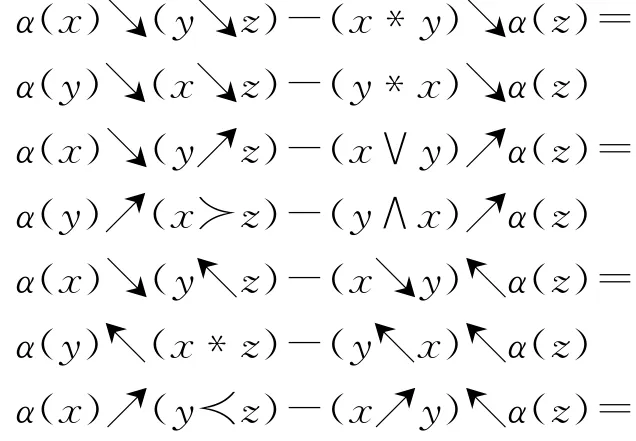
其中

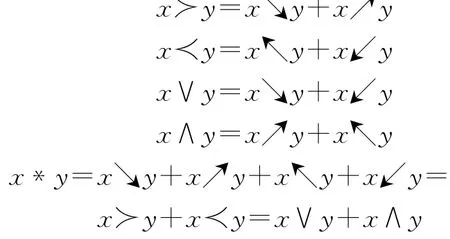
则称(A,↘,↗,↖,↙,α)为Hom-L-quadri代数。

命题3.1假设(A,↘,↗,↖,↙)是L-quadri代数,α:A→A是代数同态,令α◦↘=↘α,α◦↗=↗α,α◦↖=↖α,α◦↙=↙α,则(A,↘α,↗α,↖α,↙α,α)是Hom-L-quadri代数。

证令α◦≻=≻α,α◦≺=≺α,α◦∨=∨α, α◦∧=∧α,α◦*=*α,由Hom-L-quadri代数定义,

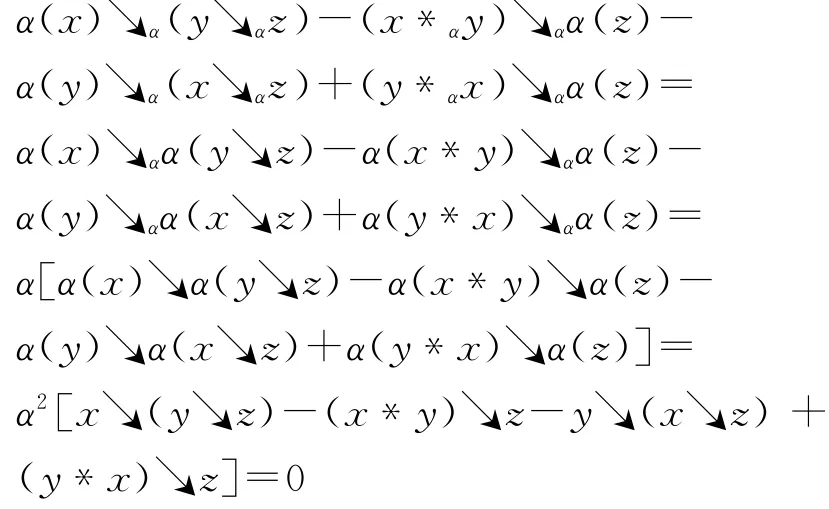
同理可证“命题3.1”的剩余4个条件。因此,(A,↘α,↗α,↖α,↙α,α)是Hom-L-quadri代数。

命题3.2假设(A,↘,↗,↖,↙,α)为Hom-L-quadri代数,

(1)如果∀x,y∈A,定义

则(A,≻,≺,α)是一个Hom-L-dendriform代数,称(A,≻,≺,α)为(A,↘,↗,↖,↙,α)的相关垂直Hom-L-dendriform代数。

(2)如果∀x,y∈A,定义

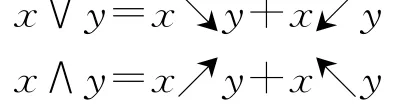
则(A,∨,∧,α)是一个Hom-L-dendriform代数,称(A,∨,∧,α)为(A,↘,↗,↖,↙,α)的相关深度Hom-L-dendriform代数。

(3)如果∀x,y∈A,定义

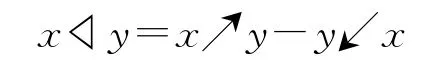
则(A,▷,◁,α)是一个Hom-L-dendriform代数,此时称(A,▷,◁,α)为(A,↘,↗,↖,↙,α)的相关水平Hom-L-dendriform代数。

证由于(1),(2),(3)的证明相似,因此只给出(3)的证明。

由Hom-L-quadri代数的定义,可得到

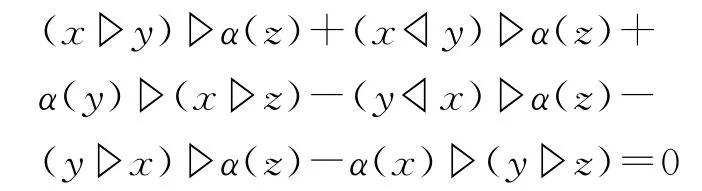
同理

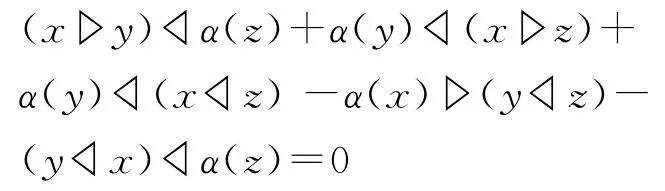
所以,(A,▷,◁,α)是一个Hom-L-dendriform代数。

推论3.1(A,↘,↗,↖,↙,α)是Hom-L-quadri代数,

(1)如果∀x,y∈A,定义

则(A,≥,α)是一个Hom-pre-Lie代数,(A,≥,α)是(A,↘,↗,↖,↙,α)的相关水平Hom-L-dendriform代数(A,▷,◁,α)的相关水平Hom-pre-Lie代数,是(A,↘,↗,↖,↙,α)的相关垂直Hom-L-dendriform代数(A,≻,≺,α)的相关水平Hom-pre-Lie代数,是(A,↘,↗,↖,↙,α)的相关深度Hom-L-dendriform代数(A,∨,∧,α)的相关水平Hom-pre-Lie代数。

(2)如果∀x,y∈A,定义

则(A,≤,α)是一个Hom-pre-Lie代数,(A,≤,α)是(A,↘,↗,↖,↙,α)的相关水平Hom-L-dendriform代数(A,▷,◁,α)的相关垂直Hom-pre-Lie代数,是(A,↘,↗,↖,↙,α)的相关垂直Hom-L-dendriform代数(A,≻,≺,α)的相关垂直Hom-pre-Lie代数,是(A,↘,↗,↖,↙,α)的相关深度Hom-L-dendriform代数(A,∨,∧,α)的相关垂直Hom-pre-Lie代数。

(3)如果∀x,y∈A,定义

则(A,[,],α)是Hom-Lie代数,是(A,↘,↗,↖,↙,α)的相关水平Hom-L-dendriform代数(A,▷,◁,α)的相关Hom-Lie代数,是(A,↘,↗,↖,↙,α)的相关垂直Hom-L-dendriform代数(A,≻,≺,α)的相关Hom-Lie代数,也是(A,↘,↗,↖,↙,α)的相关深度Hom-L-dendriform代数(A,∨,∧,α)的相关Hom-Lie代数。

证由“命题3.2”“命题2.2”和“命题1.1”即可推出。

[1]AGUIAR M,LODAY J L.Quadri-algebras[J]. Journal of Pure and Applied Algebra,2004,191:205-221.

[2]LEROUX P.Construction of Nijenhuis operators and dendriform trialgebras[J].International Journal of Mathematics and Mathematical Sciences,2004,49: 2595-2615.

[3]BAI Chengming,LIU Ligong,NI Xiang.Some results on L-dendriform algebras[J].Journal of Geometry Physics,2010,60:940-950.

[4]RONCO M.Primitive elements in a free dendriform algebra[J].Contemporary Mathematics,2000,267: 245-263.

[5]MAKHLOUF A,SILVESTROV S D.Hom-algebra structures[J].Journal of Generalized Lie Theory and Applications,2008,2(2):51-64.

[6]刘立功,倪翔,白承铭.L-quadri代数[J].中国科学:数学,2011,41(2):105-124.

Hom-L-dendriform algebras and Hom-L-quadri algebras

AN Huihui, WANG Zhichun, XUE Chen
(School of Mathematics,Liaoning Normal University,Dalian 116029,China)

Hom-L-dendriform algebras and Hom-L-quadri-algebras are the deformation of L-dendriform algebras and L-quadri-algebras respectively.The definition of Hom-L-dendriform algebra and Hom-L-quadri-algebra was introduced,and the method constructing Hom-L-dendriform algebra by an L-dendriform algebra and an algebra homomorphism,together with the method constructing Hom-L-quadri-algebra by an L-quadri-algebra and an algebra homomorphism were given.After that, the relationship among Hom-pre-Lie algebra,Hom-L-dendriform algebra and Hom-L-quadri-algebra were got.

Hom-pre-Lie algebra;Hom-L-dendriform algebra;Hom-L-quadri algebra

O152.5

:A

文章编号:1674-1404(2015)05-0387-04

2014-11-10.

国家自然科学基金资助项目(11471151).

安慧辉(1981-),女,副教授.