大动态范围高速光子相关器

刘 伟，陆文玲，王雅静，陈文钢，申 晋

引言

光子相关光谱法是研究纳米颗粒动态特性的一种有效方法。光子相关器是光子相关光谱法纳米颗粒测量系统的核心装置，该装置用于对散射光的光子脉冲进行计数，并做实时自相关运算，得到光强自相关函数，对相关函数进行反演就可以获取纳米颗粒的粒度信息。目前光子相关光谱技术的应用领域日趋广泛［1－3］，对光子相关器的处理速度和动态范围也提出了新的需求。比如，利用扩散波谱法研究颗粒的复散射现象时，要求相关器的采样时间下限达到12.5ns［4］。又如，在射电天文学等领域要求相关器具有1012的动态范围［5］。

相关器的基本结构为线性相关器，其动态范围等于相关器的通道数，即相关通道越多实现的动态范围越大。但由于实际硬件资源的限制，不可能无限制地增加相关通道，因此线性相关器的动态范围较窄。比例相关器通道间的延迟时间按照一定的比例关系增长［6］，使用较少的通道便可实现较大的动态范围，但比例相关器的动态范围与移位寄存器的数量有关，在硬件设计时很难提供所要求的移位寄存器，因此比例相关器的动态范围也受到限制。多采样时间相关器由多个线性通道组组成［7－8］，通道组分别由不同的时钟控制，因此实现的动态范围远大于线性相关器，但是随着通道数的增多，相关器的成本变得非常昂贵。

本文针对光子相关光谱技术的需求，充分利用上述相关器的优点，提出利用多采样时间相关结构来设计相关器的高速通道，利用比例相关结构来设计相关器的低速通道，并将高速通道和低速通道相结合，实现大动态范围高速光子相关器的设计。

2 相关器的基本结构

在光子相关光谱实验中，需要测量的是光强的时间自相关函数，如（1）式所示［9］：

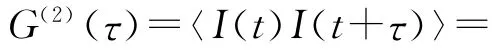
式中：I（t）及I（t＋τ）表示t及t＋τ时刻的散射光强；尖括号〈·〉表示时间平均值；T为实验时间；τ为延迟时间。在极微弱散射光的检测中，光电探测器输出的是离散的光子脉冲信号，光强I（t）是通过采样时间内的光子计数值n（t）来表示的，因此可以通过N个光子计数值的乘积和来逼近（1）式表示的积分式，即光强自相关函数的期望为［10］

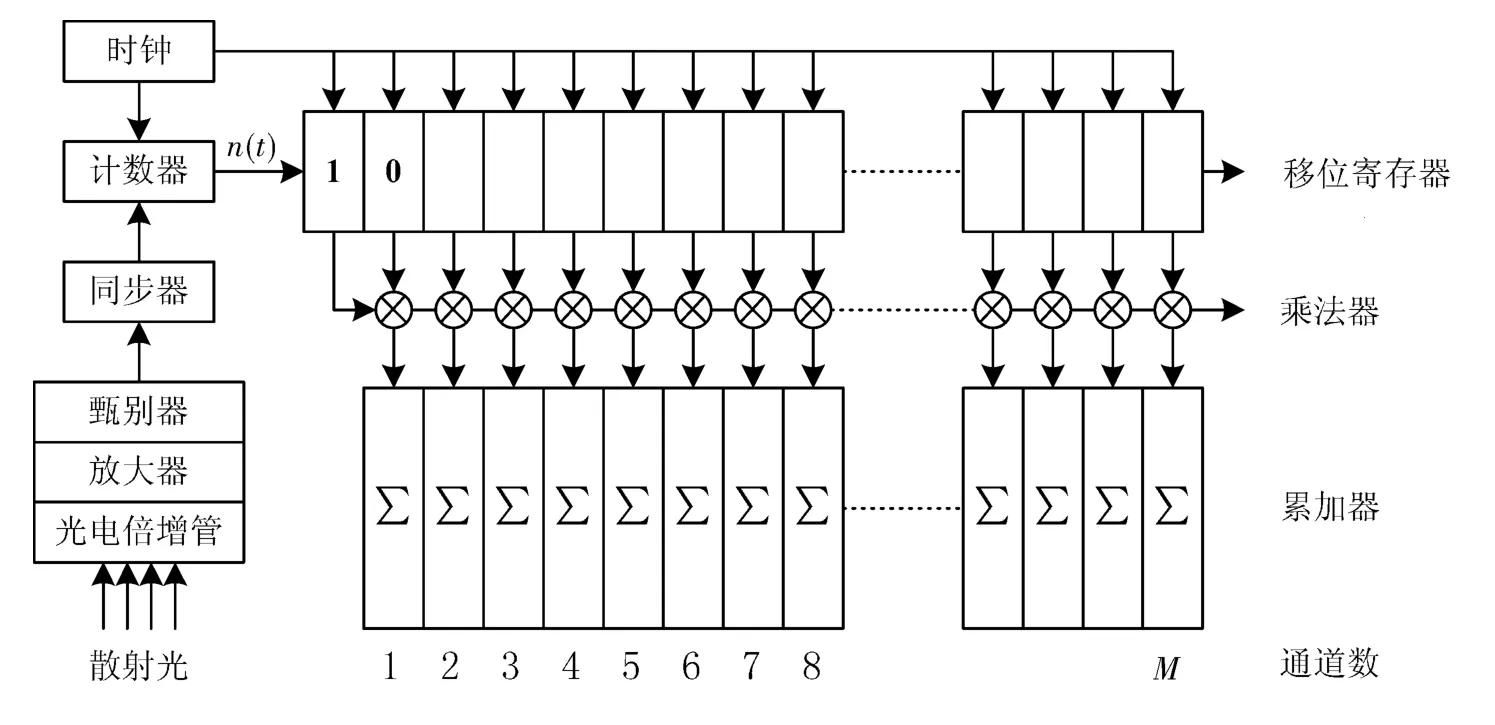
图1 线性相关器结构图Fig.1 Structure of linear correlator

为克服线性相关器的缺陷，改进的比例相关器结构如图2所示［12］。

图2 比例相关器结构图Fig.2 Structure of ratio correlator

比例相关器第k通道的延迟时间为τk＝τ·Rk－1，其中1＜R＜2，则其动态范围为Rk－1，因此可以使用较少的相关通道实现较大的动态范围，但是需要的移位寄存器数量不能减少，同时要求在运行过程中调整比例系数R，这在硬件设计上是很难实现的。

为利用较少硬件资源实现大动态范围，文献［13］提出的多采样时间相关器的结构如图3所示。

图3 多采样时间相关器结构图Fig.3 Structure of multi－tau correlator

多采样时间相关器第0组包括16个线性通道，相关函数为

式中，n0i为第0组通道当前计数值，n0i＋k为第0组第k个通道的计数值。在其余的m个相关通道组中，每组包含8个线性通道，因此相关函数为

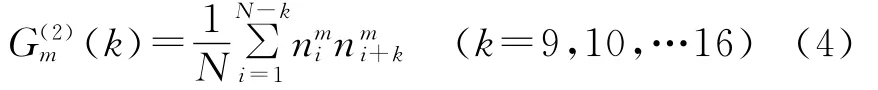
设第0组相关通道的采样时间为τ，则后续各组相关通道的采样时间为Tm＝2m·τ。每组第1通道延迟时间与采样时间相同，则每组中第k个通道的延迟时间为

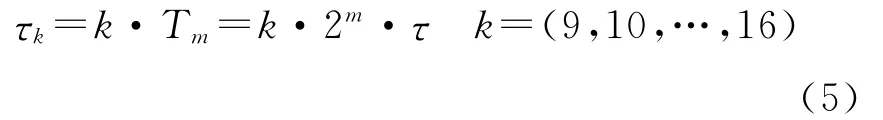
因此每组相关通道的最后一个通道延迟时间为

由此可以得出多采样时间相关器的动态范围为2m＋4，若实现1012的动态范围，则需要36个通道组，296个相关通道。因此使用多采样时间相关器可以获得大的动态范围，但是随着通道数的增多，相关器的成本变得非常昂贵。

3 大动态范围高速光子相关器

对相关函数而言，在较小的延迟时间范围内，光子脉冲信号保持较强的相关性，因此相关函数的数值最大，在较大的延迟时间范围内，信号相关性较弱，相关函数数值较小，当延迟时间超过一定数值之后，信号不再相关，相关函数的数值减小到某个数值后不再降低，这个数值称为基线。可见相关函数初始阶段包含的信息最多，一旦降到基线后，所包含的信息就很少了。因此不同延迟时间的相关函数需要不同的时间分辨率，即起始相关通道的延迟时间应该尽量短，使时间分辨率足够高，而当相关曲线衰减到基线后，则使延迟时间尽可能长，以确保相关器具有足够大的动态范围。

图4 大动态范围高速相关器结构图Fig.4 Structure of fast correlator with high dynamic range

为适应相关函数的特点，本文基于FPGA芯片设计多采样时间相关通道，作为相关器的高速通道；基于DSP芯片设计比例相关通道，作为相关器的低速通道，并将高速通道和低速通道相结合，实现大动态范围高速光子相关器，其结构如图4所示。

多采样时间相关器结构固定，在运行过程中不需要更改参数，因此非常适合使用FPGA这种大规模逻辑器件来设计实现［14］。FPGA芯片包含的硬件资源丰富，基于FPGA设计的多采样时间相关器，每个通道都包含独立的硬件乘法器和累加器，所以相关运算速度快。当FPGA芯片工作在100MHz频率时，时钟周期为10ns，通过优化FPGA的硬件乘法器和累加器，可以在单周期内完成相关数值的计算，即相关器的最小采样时间可达10ns，因此可以使用基于FPGA芯片的高速通道来计算延迟时间较小时的相关函数，实现相关器的高速运算。

比例相关器结构灵活，通过调节通道间的比例系数，可以改变其动态范围。DSP属于通用数字信号处理器，虽然运算速度相对FPGA较慢，但其具有编程灵活的特点，可在运行过程中调节比例相关器的比例系数，因此可以使用DSP芯片设计比例相关器，并将其作为低速通道，可计算延迟时间较大时的相关函数，因为当相关通道间的延迟时间较大时，不需要快速计算。同时利用DSP内部包含的大容量存储器，构建移位寄存器来存储光子计数值，实现相关器的大动态范围。

因此本文提出的大动态范围高速光子相关器结构，既减少了高速通道对硬件资源的需求，又降低了低速通道对存储器容量的要求，既实现了高速相关运算，又扩展了相关器的动态范围，同时降低了相关器的成本。

设高速通道第0组第1通道延迟时间为τff，末组最后通道延迟时间为τfl，则高速通道的动态范围为τfl／τff，设低速通道第1通道延迟时间为τdf，最后通道延迟时间为τdl，则低速通道的动态范围为τdl／τdf，那么高速通道和低速通道结合后实现的动态范围为

一般情况下设定τfl≈τdf，则大动态范围高速相关器的动态范围约为τdl／τff。如果相关器要实现1012的动态范围，高速通道分配106的动态范围，低速通道分配106的动态范围，依据等（6）式可知，高速通道需要16组136个相关通道，低速通道需要的存储区长度为220个，则实际的动态范围为2（16＋4）×220＝240≈1.1×1012。设置τff为10ns，依据等（6）式计算出τfl约为10.48ms，若设τdf为10.5ms，依据等（7）式可以计算出τdl为240×10ns≈3.1h。可见利用较少的硬件资源实现了大动态范围高速光子相关器的设计。

4 实验

为了验证所设计的大动态范围高速光子相关器，本文进行了实验。实验样品为Duke公司的3200A标准聚苯乙烯乳胶颗粒，激光器波长为532.0nm，使用光电倍增管将散射光转换为电脉冲，然后送给相关器计算得到相关函数。实验温度19.3℃。

光子相关光谱法求解颗粒粒径时，不需要知道相关函数的绝对值，因此为便于进行数据处理，对（2）式所示的光强自相关函数做标准归一化处理，如（8）式所示：

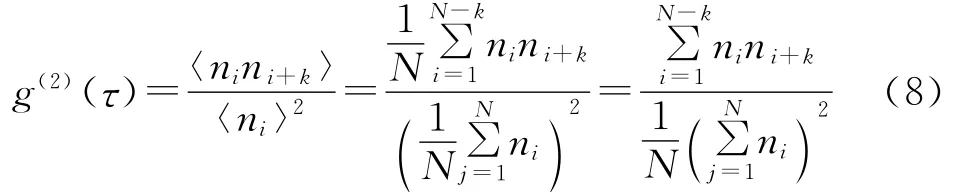
式中，分子为相关函数的数值，分母为光子平均计数值的平方，该数值也称作计算基线。标准归一化方法对自相关函数的估计存在线性偏差，特别是随着通道延时增加，动态范围增大时，偏差问题变得更加突出。文献［15］提出对称归一化方法，可以有效去除大延迟时间范围内的基线误差。文献［16］提出补偿归一化方法，该方法可去除整个延迟时间范围内的线性误差，但这两种归一化方法都需要为每一个相关通道附加监视通道，这样会占用大量的硬件资源［17］。考虑到实际参与累加运算的序列长度小于N个，特别是当通道的延迟时间较长，即k值较大，数据量又较少时，这种影响更为明显。因此将（8）式所示的归一化方法改进如（9）式所示：

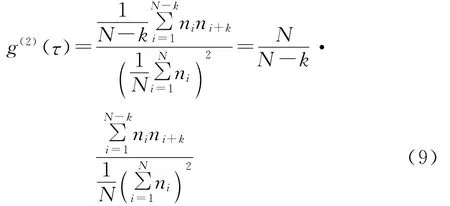
即增加系数N／（N－k）来消除基线的统计误差。同时使用相关器的最末一组通道，来近似获取延迟时间趋向无穷大时的相关函数值，并将该通道的平均值作为测量基线。为保证相关函数具有足够的精度，通常要求基线误差，即计算基线和测量基线的相对误差在0.1%以内［18］。实测的相关函数曲线如图5所示。

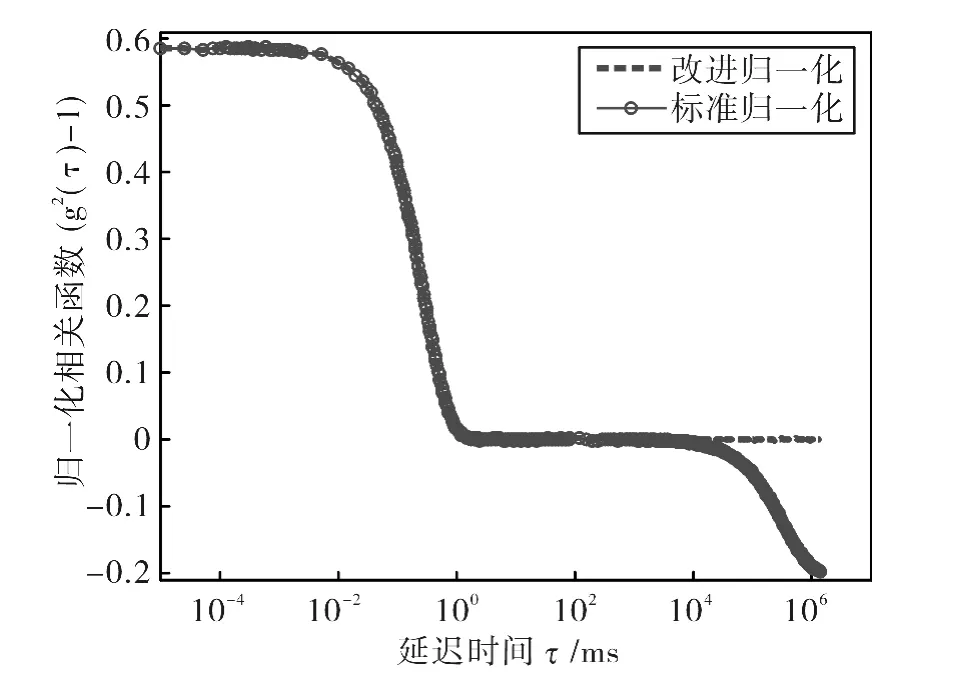
图5 实测相关函数曲线Fig.5 Measured correlation function

由实验结果可以看出，所设计的大动态范围高速光子相关器在相关函数的起始阶段时间分辨率足够高，采样时间下限达到10ns，当相关函数衰减到基线以后，又加大延迟时间，使动态范围达到1.1×1012。由图5可以看出，标准归一化方法在大延时部分严重偏离基线，而改进归一化方法较好地收敛于基线。采用改进归一化方法，当散射光强为5.0×105次／s，采样个数N 超过107时，计算基线为2.696 0×107，测量基线为2.698 5×107，基线误差为0.095%，小于0.1%的要求，因此相关函数具有足够的精度。

5 结论

本文在对比分析比例相关器和多采样时间相关器结构的基础上，充分利用这两种相关器的优点，提出利用多采样时间相关结构来设计相关器的高速通道，利用比例相关结构来设计相关器的低速通道，并将高速通道和低速通道相结合，实现了大动态范围高速光子相关器的设计。实验结果表明：大动态范围高速光子相关器的采样时间下限可以达到10ns，动态范围达到1.1×1012，采用改进归一化方法时，基线误差为0.095%，相关函数具有足够的精度，很好地满足了光子相关光谱技术的需求。

［1］ Lal J，Abernathy D，Auvray L，et al.Dynamics and correlations in magnetic colloidal systems studied by X－ray photon correlation spectroscopy［J］.The European Physical Journal E，2001，4（3）：263－271.

［2］ González－Gaitano G，Rodríguez P，Isasi J R，et al.The aggregation of cyclodextrins as studied by photon correlation spectroscopy［J］.Journal of Inclusion Phenomena and Macrocyclic Chemistry.2002，44：101－105.

［3］ Wang Haiyan，Miao Hua，Chen Yu，et al.Miniaturization design of transmission optical correlator［J］.Journal of Applied Optics，2011，32（6）：1078－1082.王海燕，苗华，陈宇，等.透射式光学相关器小型化设计［J］.应用光学，2011，32（6）：1078－1082.

［4］ Zakharov P，Cardinaux，Scheffold F.Multispeckle diffusing－wave spectroscopy with a single－mode detection scheme［J］.Physical Review E，2006，73（1）：113－120.

［5］ Shaumeyer J，Briggs M，Gammon R.Statistical fitting accuracy in photon correlation spectroscopy［J］.Applied Optics，1993，32（21）：3871－3879.

［6］ Hoppe B，Meuth H，Engels M.Design of digital correlation systems for low－intensity precision photon spectroscopic measurements［J］.IEE Proceedings on Circuits，Devices and Systems，2001，148（5）：267－271.

［7］ Schaetzel K.Correlation techniques in dynamic light scattering［J］.Journal of Applied Physics B，1987，42（4）：193－213.

［8］ Magatti D.Ferri F.Fast multi－tau real－time software correlator for dynamic light scattering［J］.Applied Optics，2001，40（24）：4011－4021.

［9］ Engels M，Hoppe B，Meuth H.Fast digital photon correlation system with high dynamic range［J］.IEEE International Asic／soc Conference，2000：18－21.

［10］Chu B.Laser light scattering：Basic principles and practice［M］.New York：Academic Press，1991：93.

［11］Lu Wenling.Study on large dynamic range and high speed photon correlator［D］.Jinan：Shandong Univer－sity of Technology，2012.

陆文玲.大动态范围高速光子相关器研究［D］.济南：山东理工大学，2012.

［12］Kojro Z，Riede A，Schubert M，et al.Systematic and statistical errors in correlation estimators obtained from various digital correlators［J］.Review of Scientific Instruments，1999，70（12）：4487－4496.

［13］Schaetzel K.New concepts in correlator design［J］.Int.Phys.Conference，1987，77：175－184.

［14］Jakob C，Schwarzbacher A T，Hoppe B，et al.A FPGA optimised digital real－time mutichannel correlator architecture［J］.IEEE Proceedings of the 10th Euromicro Conference on Digital System Design Architectures，2007：35－42.

［15］Schätzel K.Photon correlation measurements at large lag times：Improving the statistical accuracy［J］.Mod.Opt.，1988，35：711－718.

［16］Kojrot Z.Normalization and statistical noise level in the normalized autocorrelation function：compensated normalization［J］.Phys.A，1991，24：225－229.

［17］Cheng Yanting，Shen Jin，Liu Wei，et al.Normalization of autocorrelation function for multiple－tau photon correlator［J］.Chinese Journal of Lasers，2009，36（2）：444－448.

成艳亭，申晋，刘伟，等.多tau光子相关器中自相关函数的归一化方法［J］.中国激光，2009，36（2）：444－448.

［18］Zhou Zukang.Dynamic light scattering［J］.Chemistry，1986（10）：34－39.

周祖康.动态光散射［J］.化学通报，1986（10）：34－39.