基于数字图像相关技术的风电叶片静态特性试验研究

汪小平，胡雪兵，周华飞，秦良忠，朱沛东，吴洪贵

引言

近年来，风电叶片的安全保障被高度重视。风电叶片是风电机组中最关键的部件，直接影响风能利用效率及其所受载荷，很大程度上决定了风电机组整体性能和风电开发利用的经济性。风电叶片也是最易损的部件，温度、暴风雨和雷击都有可能造成叶片损伤。风电叶片还是最昂贵的部件，约占整个机组生产成本的20%［1］。因此，风电叶片的安全保障具有极端重要性。

为验证风电叶片安全，全尺寸结构测试是不可或缺的手段。国际电工委员会（IEC）要求风电叶片认证过程中需进行包括静载试验等在内的全尺寸结构测试［2］。在风电叶片静载测试方面，国外已进行了较多实践和探索。Leblanc等人［3］采用数字图像相关技术测试了风电叶片在挥舞方向单点集中荷载作用下的全场三维位移和应变。Sandia国家实验室［4］采用应变传感器测试了风电叶片挥舞方向加载下的应变。Jensen等人［5］对风电叶片挥舞方向和摆振方向同时加载，测试了其全场三维变形。目前国内风电叶片静载测试的文献报道不多。曹人靖等人［6］使用静态电阻应变仪测试了0.85m风电叶片在挥舞方向单点集中荷载作用下的静态特性。杨婷等人［7］采用静态电阻应变仪测试了风电叶片在挥舞正负和摆振正负4个方向单独加载下的应变。李海波［8］采用应变传感器进行了风电叶片挥舞方向加载下的变形测试。可见，多数已有工作仅进行了叶片单轴（单方向）加载变形测试，而双轴加载（两方向同时加载）变形测试则相对缺乏。单轴加载的缺点主要在于叶片某些区域上产生的应力、应变及损伤积累可能比设计值小，所测得的变形与叶片实际工作中的变形相差较大。而当施加挥舞方向和摆振方向合成荷载时，叶片上产生的应力分布，更接近于风电叶片实际运行过程中叶片剖面周围的应力分布，所产生的变形更符合叶片实际工作情况下的变形。这点在文献［9］和［10］中均有明确指出。此外，由上述文献可知，国内风电叶片静载试验主要采用应变传感器和位移传感器，属于传统的接触式测量方法，与被测试件连结处易发生松脱移位，所测变形误差较大。而且它们仅监测叶片离散点的结构变形。Malhotra等人［10］已指出了因离散测点非最优布置而未能获取关键响应（如极值等）的问题。不仅如此，应变／位移传感器只能测得应变／位移。数字图像相关（Digital Image Correlation，DIC）技术在上世纪80年代初提出，通过物体表面随机分布的粒子光强在变形前后的概率统计相关性来确定物体的位移或变形，具有非接触式、全场性、三维等独特优点［11－12］，且能同时测得应变和位移。国内有许多数字图像相关技术的文献报道，绝大多数为材料力学性能测试［13－14］和土木 工 程 测 试［15－16］方 面 的 应 用，而 基 于数字图像相关技术的风电叶片三维全场变形测试尚未见报道。鉴于此，作者拟采用数字图像相关技术测试风电叶片双轴（挥舞方向和摆振方向）加载下的全场三维变形，分析获得叶片在双轴荷载作用下的变形规律。

1 数字图像相关技术原理

数字图像相关技术是根据物体表面随机分布的粒子光强在变形前后的概率统计相关性来确定物体的位移或变形的非接触全场光学测量技术。其基本原理［14］是利用被测物体变形前后因测试点移动引起的光强分布函数在变形前后的2幅图像上寻找每一点对的最大相关系数，进行点的一一配对，得到点对之间的移动量，进而得到被测物体的位移场分布。具体而言，假设物体变形前被测区域的某一点O（x，y），以n×n个像素组成的微小区域E表示该点，该点变形后移至O′点，形成F区域，如图1所示。若区域F相对于区域E只发生了刚体位移，则2个区域完全相关，相关系数等于1；若2个区域发生了相对变形，则相关系数小于1。相关系数由下式确定：

式中：S1（xi，yj）；S2（xi＊，yj＊）为变形前后散斑场的待测光强分布；S1与S2为S1（xi，yj）和S2（xi＊，y＊j）的算术平均值；C为相关系数，0≤C≤1，C＝0完全不相关，C＝1表示完全相关。因此，可通过寻找最大相关系数来确定被测物体变形前后的点对关系。将被测物体划分成m个n×n像素大小的子区域E，根据最大相关系数原则寻找子区域E对应的相关子区域F，从而可得到m个点在变形过程中的相对变形量，即位移场信息。

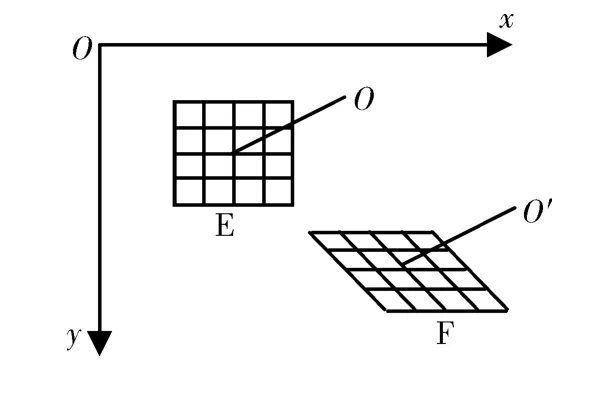
图1 数字图像相关技术原理图Fig.1 Schematics of digital image correlation technique

2 试验设计

2.1 加载试验

为探讨风电叶片双轴加载下的静态特性，本文进行基于数字图像相关技术的风电叶片全场三维变形测试试验。首先，选取一玻璃纤维增强聚酯树脂风电叶片，叶片尺寸见表1。在叶片迎风面喷涂白色亚光漆，待漆彻底干燥后用黑色碳素笔做随机散斑，其直径大小应适宜，以便摄像机能清晰拍摄到散斑。然后采用定制装置将叶片固定在一钢架上，竖向为摆振方向，横向为展向，平面外方向为挥舞方向，如图2所示。因叶片背风面物体（如钢架等）反光及自然散斑对叶片散斑的干扰，造成所拍摄的叶片图像边缘参差不齐及试验数据误差较大。为此，在叶片背风面后方合适位置悬挂一黑色幕布消除此影响［17］。最后，将一滑轮固定于叶片背风面另一钢架上，利用绳子、滑轮、砝码和沙袋作为加载装置，对叶片挥舞方向和摆振方向同时逐级加载。文献［10］表明：对风电叶片70%叶长位置加载，叶片表面产生的弯矩分布与叶片实际运行中产生的弯矩分布相接近。因此，本试验加载点设置在距叶根70%叶长（94.5cm）截面处。双轴静载试验在风电叶片挥舞方向依次施加分级荷载（1.529kg、2.038kg、2.548kg、3.058kg和3.567kg），借鉴以往风电叶片静载试验［18］，叶片摆振方向荷载按挥舞方向荷载的1.25倍取用。

表1 风电叶片的尺寸Table 1 Size of wind turbine blade

图2 试验布置Fig.2 Test setup

2.2 变形测试

加载试验布置好后，接下来准备进行叶片变形测试。根据摄像机视场和叶片尺寸大小，将摄像机放置在叶片前合适位置，以拍摄叶片整体。DIC测量系统由2部CCD摄像机组成，且要求2部摄像机至叶片任一点的直线非平行。根据风电叶片光强分布，在合适位置架设灯光，并调节适当的曝光时间，保证叶片在拍摄过程中不反光。调节摄像机镜头焦距，使摄像机能清晰显示叶片表面的散斑分布。使用点阵标定板（点与点之间的距离已知）对摄像机内外参数进行标定。标定完成后，即可进行叶片全场三维变形测试。首先，对未加载状态下的叶片进行拍摄，为叶片变形计算提供参照。然后，对叶片逐级加载，每次加载完成后，采用摄像机对变形后的叶片进行拍摄。如此重复，依次完成不同工况荷载作用下的叶片散斑图像采集。

3 试验结果及分析

3.1 噪声分析

由于摄像机的电子噪音、环境和光源的不稳定性、数据计算误差等的影响，测量噪声不可避免。正如前述，叶片变形测试过程中，每种荷载工况下，均摄取了10帧叶片数字图像。理论上，这10帧数字图像所得到的位移／应变值应完全相同。实际上，其中任意两帧数字图像得到的位移／应变值均存在差异，这说明测量过程中存在噪声影响。下面以双轴荷载（2.038kg与2.548kg）作用下的摆振方向位移和应变为例，分析DIC测量的噪声水平。表2为叶片双轴（2.038kg与2.548kg）加载下摆振方向的10组位移和10组应变的统计分析。mn为双轴加载下的各组摆振方向位移／应变测量值矩阵（一个221行1 851列的包含叶片上各点位移／应变值的数集方阵，方阵中叶片以外区域的数值均为0）。可见，DIC测量的噪声水平较低。

表2 双轴（2.038kg与2.548kg）加载下摆振方向的变形测量噪声水平分析Table 2 Noise floor in measurement of deformation under biaxial static load of 2.038 kg ＆ 2.548 kg

3.2 全场三维位移分析

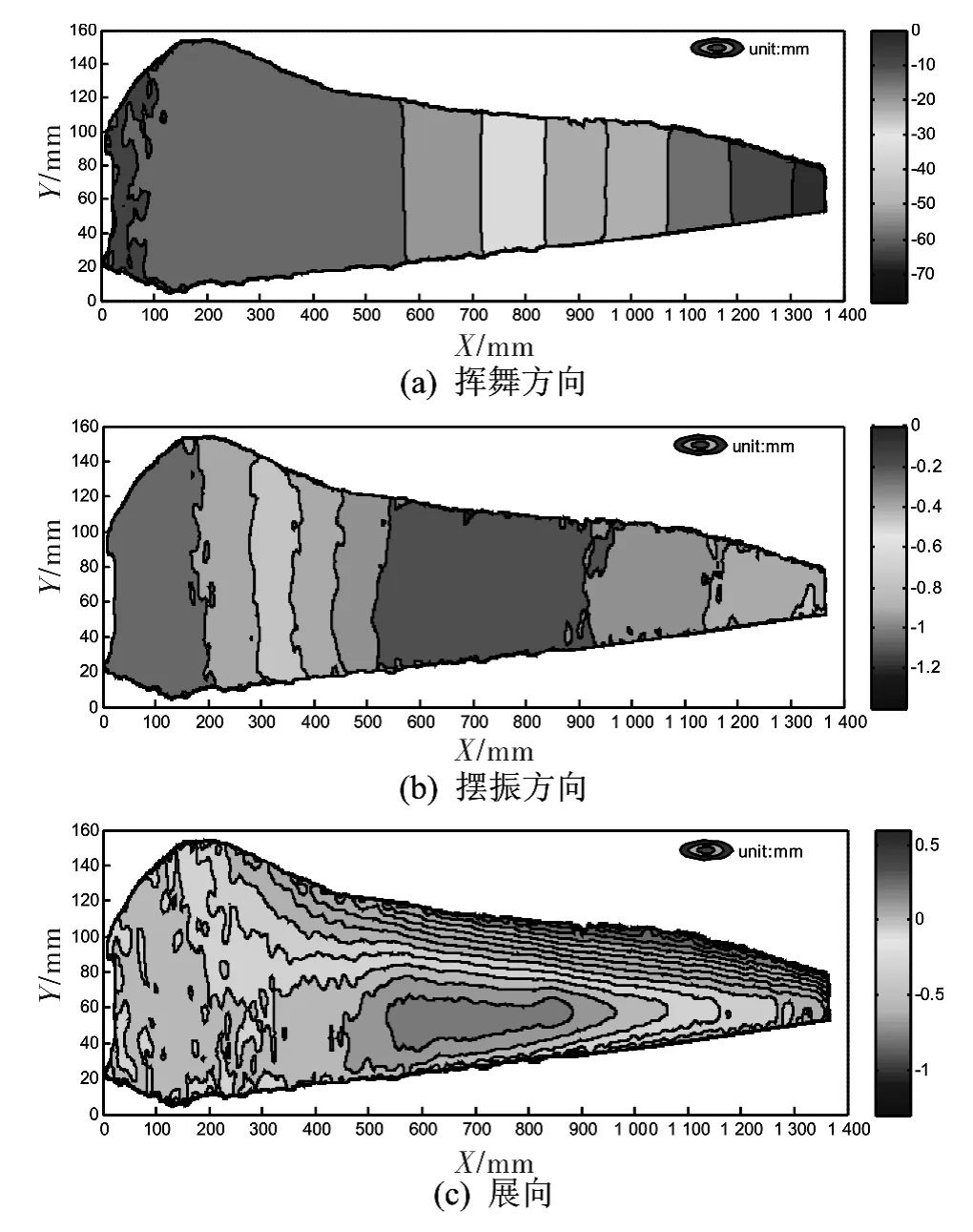
图3 风电叶片双轴（2.038kg与2.548kg）加载下的三维位移Fig.3 3D displacements of wind turbine blade under biaxial static load of 2.038 kg ＆2.548 kg

图3 为风电叶片双轴荷载（2.038kg与2.548 kg）作用下的三维位移。图中所示位移值为10组位移数据的平均值。本课题组之前已进行DIC测量精度验证，结果表明其测量精度较高［17］。限于篇幅，本文不再验证。由图3可见，叶片双轴加载下的三维位移存在以下规律：1）叶片挥舞方向位移沿展向逐渐增大，最大位移出现在叶尖。2）叶片各点的摆振方向位移均为负位移，负位移最大值出现在叶片约52%叶长（70cm）处。3）展向位移在叶根至52%叶长（70cm）区段内逐渐增大；而在52%叶长处至叶尖区段内逐渐减小。但负位移最大值出现在叶片上部局部边缘。4）展向／摆振方向位移最大值（1.3mm／1.38mm）远小于挥舞方向位移最大值（78mm）。叶片主要发生平面外弯曲，故叶片主要表现为平面外变形。此外，由于风电叶片形状不规则、加载点不在叶片重心等原因，叶片还发生平面内弯曲、叶片上部受压及下部受拉，导致叶片摆振方向位移在叶片展向中段出现负位移最大值以及叶片上部边缘出现展向负位移最大值。

其他工况荷载作用下的摆振／挥舞方向位移分布图形类似，限于篇幅，不再枚举。而展向位移在各工况荷载作用下分布不尽相似，故对其进一步分析。图4为叶片在各双轴荷载工况下的展向位移。可见，随着荷载增大，展向正位移最大值变化较小，但其出现位置由叶尖逐渐向叶根移动，直至到达距叶根约41%叶长（55cm）处（图4（d）和图4（e））。负位移最大值出现在叶片上部边缘，最大值随荷载增大而增大，出现位置则随荷载增大而逐渐向叶尖移动。

图4 风电叶片各级双轴荷载作用下的展向位移Fig.4 Spanwise displacements of wind turbine blade under different biaxial loads

对叶片在各荷载工况下的三维位移作进一步分析。图5为风电叶片各级双轴荷载作用下的三维位移分布曲线。与图3一样，图5所示位移值为10组位移数据的平均值。由图5可见：1）叶片挥舞方向位移随荷载等级增大而增大。2）加载等级越大，摆振方向位移也越大。摆振方向负位移的最大值出现在叶片展向中部。叶根至41%叶长（55cm）区域，展向位移几乎接近于0。41%叶长处至叶尖区域内，当荷载较小时（1.529kg与1.911kg），叶片平面外弯曲变形小，其迎风面纤维的受拉伸长量大于平面外弯曲的展向位移分量而产生展向正位移；随着荷载增大，叶片平面外弯曲变形增大，其展向位移分量大于迎风面纤维的受拉伸长量而产生展向负位移。

图5 风电叶片在各荷载工况下的三维位移分布曲线Fig.5 Curves of 3D displacements of wind turbine blade under different biaxial loads

3.3 全场三维应变分析

图6 为风电叶片在双轴荷载（2.038kg与2.548kg）作用下的三维应变。可见，应变分布无明显规律。这是由于叶片材质不均匀，叶片表面为曲面，加载点未作用于叶片重心及叶片自身重力等，叶片受载后处于弯扭耦合复杂受力状态，使得叶片表面产生正负应变且散开分布。展向、摆振方向及剪切方向应变范围分别为－0.05～0.25，－0.20～0.30，－0.20～0.15。其他荷载工况下的应变有类似结果，不再赘述。

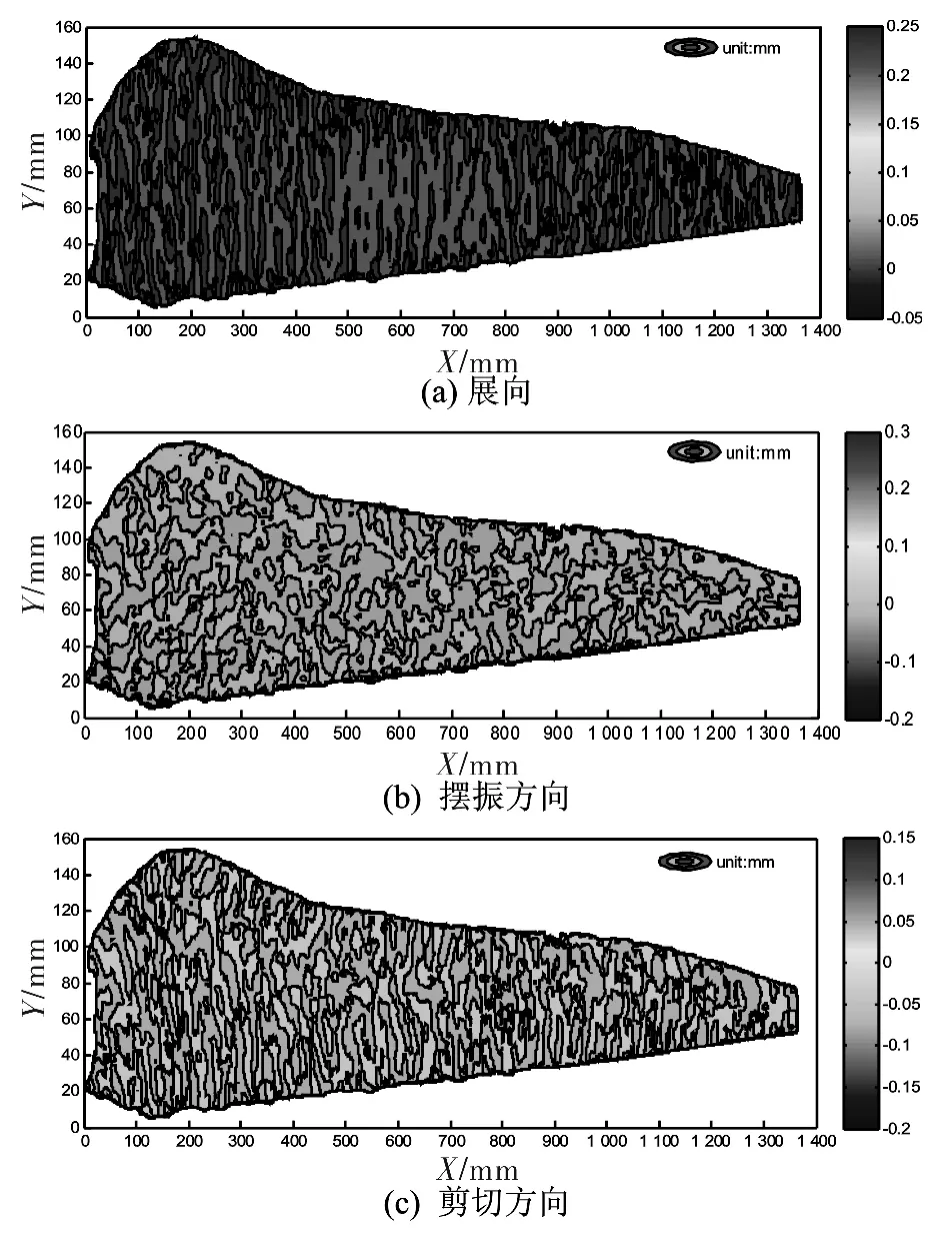
图6 风电叶片双轴（2.038kg与2.548kg）加载下的三维应变Fig.6 3D strains of wind turbine blade under biaxial load of 2.038 kg ＆2.548 kg

4 结论

本文采用数字图像相关技术测量风电叶片在挥舞方向与摆振方向同时加载下的全场三维变形，获得了叶片在双轴加载下的三维变形规律。可得以下几个重要结论：

1）在各工况荷载作用下，风电叶片的三维位移分布具有良好规律，而应变分布则无明显规律。此外平面外位移大于平面内位移。

2）挥舞方向位移沿展向逐渐增大，最大值出现在叶尖。

3）叶片各点的摆振方向位移均为负位移，负位移最大值出现在叶片中部。

4）叶根至41%叶长（55cm）区域，展向位移几乎接近于0.41%叶长处至叶尖区域内，当荷载较小时（1.529kg与1.911kg），叶片平面外弯曲变形小，其迎风面纤维的受拉伸长量大于平面外弯曲的展向位移分量而产生展向正位移；随着荷载增大，叶片平面外弯曲变形增大，其展向位移分量大于迎风面纤维的受拉伸长量而产生展向负位移。

［1］ Burton T，Sharpe D，Jenkins N，et al.Wind energy handbook［M］.New York：John Wiley ＆ Sons，2001：1－609.

［2］ International electrotechnical commision.IEC 61400－22wind turbines part 22：comformity testing and certification［S］. Geneva：International Electrotechnical Commision，2010：1－59.

［3］ Leblanc B，Niezrecki C，Avitabile P.et al.Full－field inspection of a wind turbine blade using three－dimensional digital image correlation［C］.Bellingham，Washington：SPIE Proceedings，2011：1－12.

［4］ Paquette J，Vandam J，Hughes S.Structural testing of 9mcarbon fiber wind turbine research blades［C］.Reno，Nevada：the AIAA 2007Wind Energy Symposium，2007：1－12.

［5］ Jensen F M，Branner K，Nielsen P H，et al.Full scale test of a 34mbox girder 1：Data report［C］.Roskilde，Denmark：RisφNational Laboratory for Sustainable Energy，2008：1－151.

［6］ Cao Renjing，Liu Daoxing.Experimental investigation on static structrual characteristics of a horizontal axis wind turbine［J］.Acta Energiae Solaris Sinica，2001，4（22）：436－439.

曹人靖，刘道新.水平轴风力机风轮静态结构特性实验研究［J］.太阳能学报，2001，22（4）：436－439.

［7］ Yang Ting，Deng Wenchao，Yang He，et al.Static load strain test of wind turbine blades［J］.Research and Exploration in Laboratory，2011，11（30）：33－35，39.

杨婷，杜文超，杨贺，等.风电叶片静载荷应变测试试验［J］.实验室研究与探索，2011，11（30）：33－35，39.

［8］ Li Haibo.Static test and analysis for wind turbine blades［J］.Power System and Clean Energy，2013，4（29）：100－104.

李海波.风力机叶片静力测试与分析［J］.电网与清洁能源，2013，4（29）：100－104.

［9］ China National Standardization Management Committee.GB／T 25384－2010Full－scale structure test of wind turbine blades of wind turbine［S］.Beijing：China Standard Press，2010：1－48.

中国国家标准化管理委员会.GB／T 25384—2010风力发电机组风轮叶片全尺寸结构试验［S］.北京：中国标准出版社，2010：1－48.

［10］Malhotra P，Hyers R W，Manwell J F，et al.A review and design study of blade testing systems for utility－scale wind turbines［J］.Renewable and Sustainable Energy Review，2012，16（1）：284－292.

［11］Yamaguchi I.A laser－speckle strain gauge［J］.Journal of Physics E：Scientific Instruments，1981，14（11）：1270－1273.

［12］Peters W H，Ranson W F.Digital image techniques in experimental stress analysis［J］.Optical Engineering，1982，21（3）：427－431.

［13］Rui Jiabai，Jin Guanchang，Xu Bingye.A new digital speckle correlation method and its application［J］.Acta Mechanica Sinica，1994，26（5）：599－607.

芮嘉白，金观昌，徐秉业.一种新的数字散斑相关方法及其应用［J］.力学学报，1994，26（5）：599－607.

［14］Yao Xuefeng，Lin Bisen，Jan Longhui，et al.Threedimensions deformation field measurement combining digital speckle correlation technology with stereo photography［J］.Optical Technique，2003，29（4）：473－476，479.

姚学锋，林碧森，简龙晖，等.立体摄影术与数字散斑相关方法相结合应用研究三维变形场［J］.光学技术，2003，29（4）：473－476，479.

［15］Shan Baohua，Ou Jinping，Zhao Renxiao，et al.Principles and applications of speckle image correlation digital technique［J］.Journal of Experimental Mechanics，2003，18（3）：409－418.

单宝华，欧进萍，赵仁孝，等.散斑图像相关数字技术原理及应用［J］.实验力学，2003，18（3）：409－418.

［16］Sun Wei，He Xiaoyuan.Experimental studies on application of digital image correlation in measuring field of civil engineering［J］.Journal of Nanjing University of Aeronautics and Astronautics，2009，41（2）：271－275.

孙伟，何小元.数字图像相关方法在土木测试领域中的实验研究［J］.南京航空航天大学学报，2009，41（2）：271－275.

［17］Dou Hongyao.Test and analysis of full－field 3Ddeformation for a wind turbine blade［D］.Qinhuangdao：Yanshan University，2014.

豆红尧.风电叶片全场三维变形测试及分析［D］.秦皇岛：燕山大学，2014.

［18］Branner K，Berring P，Berggreen C，et al.Torsional performance of wind turbine blades－part II：numerical validation［C］.Kyoto：Sixteenth International Conference on Composite Materials，2007：1－10.