基于光线追迹的单频激光多重回馈效应研究

曾召利，杜双格，张晓军，刘渊声，尚永兵，李维娜，张 敏

引言

激光回馈是指激光器的输出光被外部物体反射后，其中一部分光返回到激光器谐振腔，回馈光携带了外部物体的运动信息，与腔内光场发生自混合干涉后，调制激光器强度输出的现象［1－3］。根据回馈光在回馈外腔中往返次数的不同，激光回馈可分为单重回馈、双重回馈和多重回馈等［4－6］。激光单重回馈是指激光在回馈外腔中往返一次后就返回到激光谐振腔，调制激光器产生类似于双光束干涉的光学条纹，每个条纹对应二分之一波长的位移，即激光单重回馈系统的分辨率为半个波长（对于632.8nm的氦氖激光波长，其分辨率为316.4nm）。

激光多重回馈是指激光在回馈腔内经历几十次甚至上百次往返，再返回到激光谐振腔，形成多重回馈，其优点是能够对半波长条纹进一步光学细分，可达纳米级分辨率。为此，国内外研究者对激光多重回馈现象进行了深入研究［7－10］，实现了对半个波长条纹的8细分［11］、甚至40细分［12］（对于632.8nm的氦氖激光波长，其分辨率达到8nm）。但是，在多重回馈系统中，由于采用了特殊的非准直平凹回馈腔结构，回馈光在平凹回馈腔内的传输规律比较复杂，对获得的调制幅度不均匀、存在大包络的回馈条纹的产生机理还不十分清楚。

本文建立了一种基于非准直平凹回馈腔的光线追迹模型，采用该模型对单频激光多重回馈效应进行了研究，解释了多重回馈中的各种条纹现象及产生机理。根据光线追迹的分析计算，获得了不同回馈镜倾角时多重回馈的回馈阶次和耦合系数等参数，明确了影响回馈条纹形状的主要因素，包括回馈镜倾角、曲率半径、反射率以及回馈外腔长等。

1 实验装置

基于非准直平凹回馈腔的单频激光多重回馈系统如图1所示。其中腔镜M1、M2组成半外腔氦氖单纵模激光器，凹面镜 M1的反射系数r1＝0.996，曲率半径为1 000mm，平面镜M2的反射系数r2＝0.994，T为激光增益管，激光谐振腔长为120mm。腔镜M2与回馈镜M3组成非准直回馈外腔，M3与激光轴线之间有微小倾角θ，M3的反射系数为r3＝0.998，曲率半径为R＝500mm，回馈外腔长为100mm（实验中可调节）。在非准直回馈腔中，M2固定不动，M3固定在压电陶瓷（PZT）上，PZT加载有20Hz三角波电压，驱动回馈镜M3往返运动，以改变外腔长；由于回馈镜镀有高反膜，激光输出会在回馈外腔中多次往返后，再返回到激光谐振腔中，从而形成多重回馈。ATT为衰减片，用于适当调节回馈光强。探测端的输出光经分光镜BS分成两部分，一部分入射到扫描干涉仪SI观察激光器的模式；另一部分由光电探测器D1接收后，输入到示波器OS显示和存储。

图1 基于平凹回馈腔的单频激光多重回馈系统Fig.1 Single frequency laser multiple feedback system based on plane－concave cavity

2 实验现象

采用基于非准直平凹回馈腔的单频激光多重回馈系统，对回馈镜在不同倾角时的多重回馈现象进行了研究。实验结果如图2所示。为便于多重回馈与单重回馈的现象对比，实验中首先采用反射率为0.04的回馈镜，获得了单重回馈的光强调制曲线，如图2（a）所示；然后，换用反射率为0.998的回馈镜，缓慢调节回馈镜倾角θ，使θ从0°开始逐渐增大，同时在PZT上施加三角波电压，此时获得的多重回馈光强调制曲线如图2（b）～（g）所示。

从图2（a）可以看出，当回馈镜M3的反射率较小（弱回馈）时，激光器输出光强随外腔变化的曲线为类正弦形状，而且回馈镜每移动半个波长位移就产生一个回馈条纹，该现象即为传统单重回馈效应。从图2（b）、（d）、（f）可以看出，在回馈镜倾斜时，激光输出仍受到外腔长调制，但与传统单重回馈相比，多重回馈使回馈条纹密度明显增大，条纹周期明显减小。通过对比相同时间周期内的回馈条纹数，发现多重回馈条纹的密度可以达到传统弱回馈条纹密度的25倍以上。从图2（b）和（c）可以看出，在倾角为0.6′时，回馈条纹的调制幅度并不相同，整个回馈条纹曲线存在有大包络现象。图2（d）和2（e）显示，当倾斜角增大到1.2′时，回馈条纹的调制幅度逐渐变得均匀，但回馈条纹的密度并没有改变。当回馈镜倾斜角继续增大到1.7′时，从图2（f）和2（g）可以看出，回馈条纹的调制幅度已变得十分均匀，大包络基本消失，此时得到了稳定的、条纹密度数十倍于传统弱回馈的多重回馈条纹，每个回馈条纹对应的分辨率约为λ／50。图2（a）是传统回馈调谐曲线；图2（b）和（c）是回馈镜倾斜角θ为0.6′；图2（d）和（e）是回馈镜倾斜角θ为1.2′；图2（f）和（g）是回馈镜倾斜角θ为1.7′；其中图2（c）、（e）、（g）分别是图2（b）、（d）、（f）的放大图。

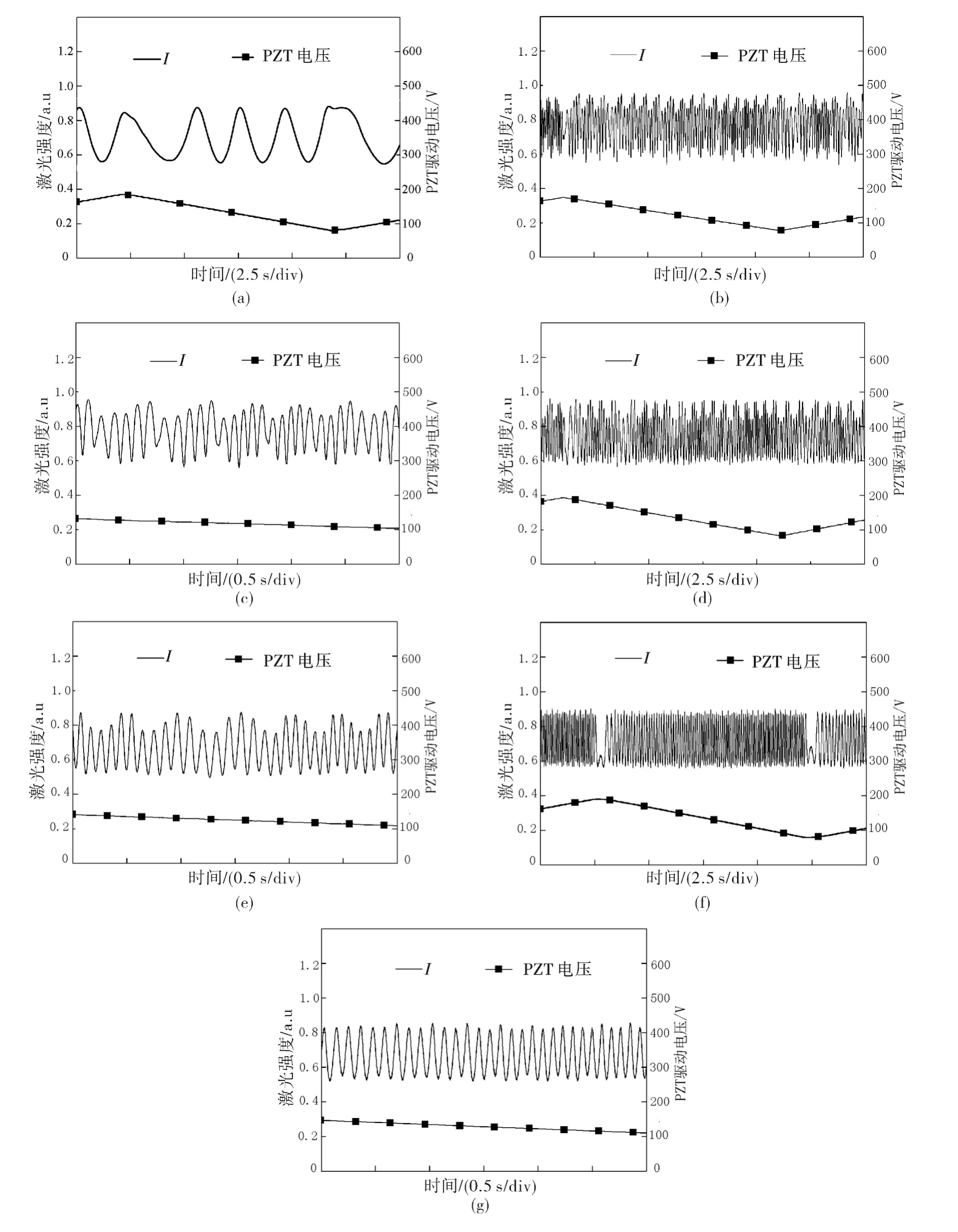
图2 不同倾斜角时的多重回馈实验结果Fig.2 Experimental results of multiple optical feedback when tilted angle is different

3 光线追迹分析

实验结果表明，在基于非准直平凹腔的多重回馈系统中，我们获得了高分辨率的回馈条纹，该条纹在没有任何电子细分条件下可以达到纳米量级，而且还具有进一步提高的潜力，这对研究高精度回测量系统具有重要意义。然而，由于多重回馈系统比较复杂，目前对高分辨率回馈条纹的产生机制还有待深入研究，同时对影响回馈条纹形状的因素以及不同倾角下回馈条纹调制幅度不均匀等现象也未能很好解释。

在腔镜M2和回馈镜M3组成的非准直平凹回馈腔中，M2与 M3都镀有高反射膜，而且M3与激光轴线之间有微小倾角，使得激光输出会在平凹回馈腔内经历几十次甚至上百次往返后才返回到激光谐振腔，并且一般有多条经历了多次往返的回馈光都能返回到激光谐振腔，从而形成多重回馈。然而，由于回馈镜M3的直径较小（20mm），几十个反射光斑集中分布在回馈镜中央10mm范围内，反射光斑之间互相重叠，人眼无法观察到激光束究竟在平凹腔内往返了多少次后才返回到激光谐振腔，所以无法知道回馈光的阶次，也无法获得准确的条纹分辨率；同时，由于回馈光在激光腔镜上相互重叠，将无法知道到底有几条经历了多次往返的回馈光束能够通过毛细管返回到激光谐振腔，也就无法解释多次回馈条纹形状的变化特点。从以上分析可知，多重回馈的各种现象本质上是由平凹回馈系统的几何结构所决定，而光线追迹法对于分析激光束在回馈腔内的几何传输规律十分方便。

基于非准直平凹回馈腔的光线追迹模型如图3所示。在平凹回馈腔中，反射光斑在回馈腔镜面上是沿直线分布的，反射光束在凹面回馈镜上的投影可以看做一个圆弧，其方程为

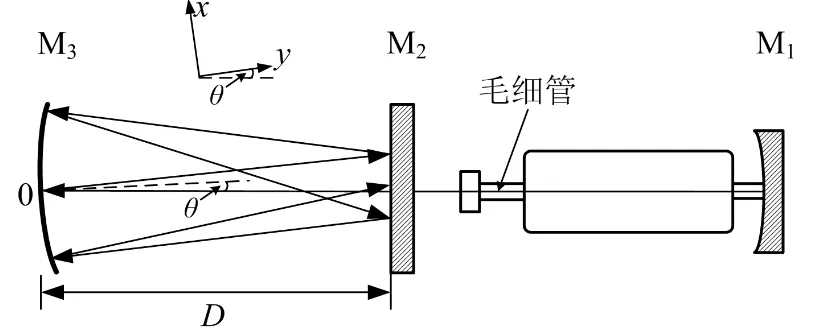
图3 非准直平凹回馈腔光线追迹示意图Fig.3 Schematic of ray tracing based on asymmetric plane－concave feedback cavity

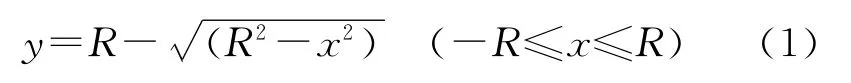
式中R为凹面回馈镜的曲率半径，坐标原点为圆弧的中心顶点。

腔镜M2为平面镜，它与凹面回馈镜 M2之间的距离为D，反射光束在平面镜上的投影可以看作一条直线，其方程可表示为

式中：θ为凹面镜的倾斜角；α＝tanθ。

凹面镜圆弧上经过（x0，y0）点的法线方程为

凹面镜圆弧上经过（x0，y0）点的切线方程为

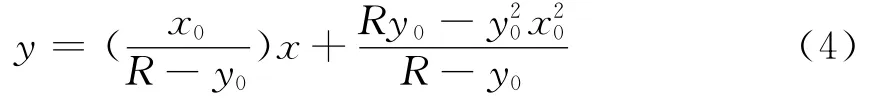
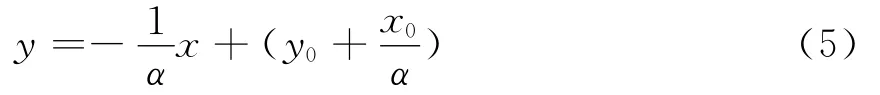
激光束入射到平凹回馈腔时，入射光线的方程为

平面镜直线经过（x0，y0）的法线方程为

由方程（1）～（6）可依次求出入射光与凹面镜的交点位置以及反射光与平面镜的交点位置，同时对每次反射设置一定的反射损耗，当最后的光强小于初始光强的5%时，认为回馈光在平凹腔内的反射结束。由于He－Ne激光器的毛细管非常小（直径约1mm），能够返回到激光谐振腔内的光束只能是毛细管的旁轴光束。所以，除了满足回馈光强条件外，能够返回到激光谐振腔的反射光斑的位置应该在凹面镜第一个反射光斑附近（两光斑距离小于0.5mm），才能形成有效回馈。回馈光束返回到激光腔与内部光场进行耦合的强弱称为耦合系数η，其大小主要由回馈光斑与毛细管截面的重叠面积决定。

当回馈腔长D＝100mm，回馈镜的曲率半径R＝500mm，回馈镜的倾斜角θ＝0.6′时，采用光线追迹得到回馈光束的有效阶次分别为第25阶（即在平凹回馈腔中往返了25次的回馈光束，η＝0.21）、第17阶（η＝0.14）和第5阶（η＝0.31），由于返回激光器的3条回馈光束的耦合系数η比较接近，根据叠加原理，得到的回馈曲线将具有大包络的特点，这与图2（b）和2（c）的实验曲线吻合得较好；当回馈镜的倾斜角为θ＝1.2′时，得到的有效阶次分别为第25阶（η＝0.30）、第17阶（η＝0.08）和第5阶（η＝0.18），此时能够返回到激光器的回馈光束主要是第25阶和第5阶，得到的回馈曲线的大包络会稍微平滑一些，这与图2（d）和2（e）的实验曲线吻合得较好；当倾斜角θ＝1.7′时，能够返回到激光谐振腔的有效阶次为第25阶（η＝0.38）和第5阶（η＝0.05），由于第5阶的耦合系数比第25阶小很多，因此叠加效应不再明显，回馈条纹的大包络现象将消失，这与图2（f）和2（g）的实验曲线吻合得很好。

追迹结果表明，由于非准直平凹腔的特殊结构，反射光束在平凹腔内的反射比较复杂，一般会有多条经历了多次往返的回馈光束满足有效回馈条件，形成多重回馈，而且有效回馈光的条数还会随着外腔参数的变化而改变。采用光线追迹法不但验证了多重回馈的确是由多条回馈光束共同作用的结果，而且还确切知道了能够返回到谐振腔的回馈光的阶次及其耦合系数。

4 结论

提出了一种基于非准直平凹腔的激光多重回馈光线追迹模型。采用光线追迹对激光多重回馈的有效回馈阶次、耦合系数进行了计算；对激光多重回馈条纹的产生机理与条纹特性进行了研究；对影响多重回馈条纹形状的主要因素进行了分析；对回馈镜倾斜角与回馈条纹之间的关系进行了模拟，理论分析与实验结果吻合得很好。基于光线追迹的分析模型为研究多重激光回馈效应提供了一种新的方法和思路。

［1］ Li Duo，Wan Xinjun，Zhang Shulian.Laser feedback interferometeric system for both displacement and absolute distance measurement［J］.Journal of Applied Optics，2007，28（4）：496－500.

李铎，万新军，张书练.具有位移和绝对距离测量能力的回馈干涉系统［J］.应用光学，2007，28（4）：496－500.

［2］ Xu Jun，Zhao Tianpeng，He Deyong，et al.Im

provement of laser ranging precision using the selfmixing effect in a single－mode VCSEL［J］.Opto－E－lectronic Engineering，2006，33（12）：27－31.

徐军，赵天鹏，何德勇，等.单模VCSEL激光自混合测距精度的提高［J］.光电工程，2006，33（12）：27－31.

［3］ Cui Liu，Zhang Shulian.Feedback displacement measurement system using dual－freuqency He－Ne laser［J］.Journal of Applied Optics，2007，28（3）：328－331.

崔柳，张书练.双频氦氖激光回馈位移测量系统的实验与应用研究［J］.应用光学，2007，28（3）：328－331.

［4］ Xia Wei，Zhou Xiuzhen，Wang Ming，et al.Selfmixing interference in dual－wavelength fiber ring laser using cascaded fiber Bragg gratings［J］.Optics＆Laser Technology，2013，52：43－47.

［5］ Zhang Shulian，Wolfgang Holzapfel.Orthogonally polarization in lasers：physical phenomena and engineering applications［M］.New Jersey：John Willy ＆Sons Inc.2013.

［6］ Zhang Shulian，Tan Yidong.Orthogonally linearlypolarized lasers and its new application in precision measurement ［J］. Opto－Electronic Engineering，2009，36（3）：1－11.

张书练，谈宜东.正交线偏振激光器及其在精密测量中的新应用［J］.光电工程，2009，36（3）：1－11.

［7］ Hong Y，Spencer P，Shore K，et al.Noise characteristics of a single－mode laser diode subject to strong optical feedback［J］.Journal of Lightwave Technology，2002，20（10）：1847－1850.

［8］ Mao Wei，Zhang Shulian.Effects of optical feedback in a birefringence－Zeeman dual frequency laser at high optical feedback levels［J］.Applied Optics，2007，46（12）：2286－2291.

［9］ Zeng Zhaoli，Zhang Shulian，Tan Yidong.Laser feedback interferometry based on high density cosinelike intensity fringes with phase quasi－quadrature［J］.Optics Express，2013，21：10019－10024.

［10］Mao Wei，Zhang Shulian，Fei Ligang，et al.Highfrequency intensity modulation in orthogonal polarized dual frequency lasers with optical feedback［J］.Applied Optics，2006，45（33）：8500－8505.

［11］Tan Yidong，Zhang Shulian，Liu Weixin，et al.Intensity modulation in single－mode microchip Nd：YAG lasers with asymmetric external cavity［J］.Chinese Physics，2007，16（4）：1020－1026.

［12］Fei Ligang，Zhang Shulian.The discovery of nanometer fringes in laser self－mixing interference［J］.Optics Communications，2007，273（1）：226－230.