利用多模卫星导航系统加快PPP的收敛速度
宋 超郝金明
(解放军信息工程大学导航与空天目标工程学院郑州450001)
利用多模卫星导航系统加快PPP的收敛速度
宋 超†郝金明‡
(解放军信息工程大学导航与空天目标工程学院郑州450001)
精密单点定位(Precise Point Positioning,PPP)不需要基准站的支持,具有广阔的应用前景.但是PPP获得高精度定位需要一个收敛过程.为了加快PPP的收敛,讨论利用多模卫星导航系统加快PPP的收敛.实验表明多模卫星导航系统使用了更多的观测量,收敛速度明显加快,三维误差收敛到10 cm、15 cm和20 cm需要时间减少的平均百分比分别为42%、78%和74%.同时也表明在山区等卫星高度截止角较高的困难地区,在单一系统无法实现定位的情况下,多模卫星导航系统也可以明显加快PPP的收敛,获得较好的定位结果.
天体测量学,地球,技术:其他诸多方面,方法:数据分析
1 引言
精密单点定位自从1997年被提出以来获得了长足的发展[1],目前正逐步在实践中应用.PPP使用精密轨道和精密钟差[2],并利用模型改正或者估计各项误差源,进而获得高精度定位结果.相对于网络RTK、普通RTK等作业方法,PPP不需要基准站的支持,仅仅利用单台接收机就可以获得高精度定位,所以PPP的应用前景非常广阔,特别是在海上、山区等架设基准站比较困难的地区.2013年4月1日国际GNSS组织(IGS)发布了实时精密星历和精密钟差,进一步推动了PPP的实时应用[3].
然而,PPP有一个无法回避的缺点,即PPP获得高精度定位需要一个收敛过程[4].一般来讲,PPP的收敛需要几十分钟,在观测条件较差的情况下,收敛时间会更长.所以研究如何加快PPP收敛对于用户具有重要的意义.从本质上讲,PPP收敛慢的原因有两个[5],一是伪距观测量精度较低,二是卫星空间几何构型变化较慢.从普通用户来讲,导致PPP收敛慢的两个原因是客观存在的,也无法完全消除.事实上,从测量角度来讲,增加观测量个数可以提高估计参数精度,进而加快PPP的收敛.增加观测量个数有两个途径,一是增加频率个数,比如从双频变成三频[6−7];二是增加卫星个数,比如使用多个卫星导航系统的数据,增加观测卫星的个数.本文仅探讨后者,即使用多模卫星导航系统增加观测卫星个数.
关于多模卫星导航系统的定位,国内外有许多研究[8−9].有利用多模卫星导航系统进行组合单点定位[10−11],也有利用多模卫星导航系统进行精密单点定位提高解算的精度[12−18],这些研究主要着眼于增强定位的可靠性等,讨论的背景是观测条件较好的情况,对于观测条件比较恶劣的地区,比如在山区,没有讨论.同时也可以进行时间频率的传递[19].Trimble公司利用全球布设的100多个测站实时估算精密轨道和钟差,在绝大部分情况下,PPP可以在半小时内完成收敛,如果将Galileo系统和北斗系统加入,收敛时间能减少一半[20].此外,Trimble公司的RTX(Real Time eXtended)服务估计对流层延迟参数、电离层延迟参数和硬件偏差参数等,可以在极短时间以内(比如分钟量级)完成收敛[21],极大地促进了实时PPP的应用.但是RTX服务依托了大量的地面参考站(参考站间距约为120 km),这对用户提出了较高的要求,因为用户需要在周围布设参考站,大大增加了成本.
本文着重利用多模卫星导航系统加快PPP的收敛.首先探讨多系统下的PPP模型,然后利用实验数据进行分析.
2 多系统PPP模型
PPP一般使用消电离层组合模型,相应的观测方程为

由于不同卫星导航系统之间有系统性偏差,参数估计时需要考虑.与广播星历不同,精密星历使用的是ITRF(International Terrestrial Reference Frame),系统之间差别不大.所以系统性偏差中影响最大的是系统间时间偏差,目前不同卫星导航系统之间的时间偏差无法用准确的规律表达出来.对于用户来讲最好的方式就是将系统时间偏差并到接收机钟差里面,即每增加1个系统,钟差参数就增加1个.
假设有2个系统,观测卫星数分别为m和n个,则相应的观测模型为
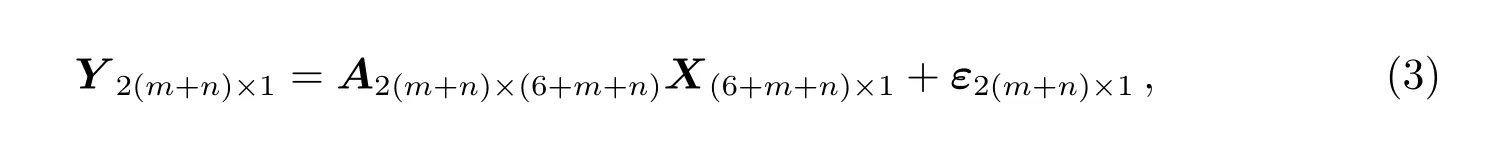
其中X(6+m+n)×1=[x,y,z,ztd,δt1,δt2,N1...Nm+n]表示待估计参数,分别为接收机坐标(x,y,z)、接收机钟差2个(δt1,δt2)、天顶对流层延迟ztd和消电离层组合模糊度N1... Nm+n,A2(m+n)×(6+m+n)表示设计矩阵,Y2(m+n)×1表示消电离层组合观测量.
设计矩阵A2(m+n)×(6+m+n)为

其中e表示视线矢量,M表示对流层映射函数,I表示全1矩阵,O表示全0矩阵,E表示单位矩阵.
上面表示的是2个系统,如果有更多的系统,则每增加1个系统,钟差参数相应增加1个,A阵和X阵相应扩展即可.
卫星的载波相位和伪距观测值的方差为
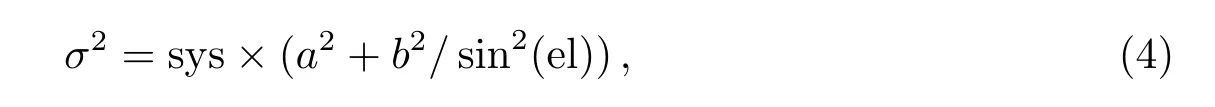
el表示卫星高度角.对于载波相位观测值a=b=3 mm,而对于伪距观测值a=b=3 dm,sys表示不同卫星导航系统之间的权重,有许多种方法可以确定,一般根据卫星导航系统实际运行情况设置,比如设置GPS为1,GLONASS为1.2,BDS为1.2.
对观测值的方差阵求逆即可得到观测值的权阵P.然后按照扩展Kalman滤波可以估计参数,获得定位结果.
3 实验分析
3.1 多模卫星导航系统的效果
目前全球卫星导航系统主要有4个:GPS、GLONASS、BDS和Galileo.由于目前Galileo系统仅有少量的几颗卫星,而BDS的卫星天线相位中心偏差和相位中心变化参数尚未准确标定,所以下面主要使用GPS+GLONASS组合来增加观测卫星数目.
选取IGS测站yar3考察收敛效果.数据采样间隔为30 s,卫星高度截止角选为15◦.以单系统GPS作为比照,考察GPS+GLONASS组合系统的PPP收敛效果.卫星数和PDOP(Position Dilution of Precision)值如图1所示,非常明显多系统卫星数目显著增加,PDOP值显著降低.
3个方向误差图如图2所示,多系统的收敛速度比单系统快.在图2中,东方向误差收敛到2 cm时GPS系统用了400个历元,而多系统仅仅用了100个历元.这种优势在北方向和高程方向更加明显.
为了进一步展现收敛效果,连续计算一周的数据,三维误差变化如图3所示.从图上可以看出,整体上多系统的收敛速度明显比单系统要快得多,这在第101天至第104天中反映得尤其明显.第105天至第107天多系统的收敛速度优势虽然不如前4天明显,但是总体来讲仍然优于单系统的收敛速度.
下面统计三维误差收敛到10 cm、15 cm和20 cm需要的时间.为了准确反映收敛速度,下面定义收敛到某个精度的统计方法.以10 cm为例,如果从某一个时刻开始,三维误差一致小于10 cm,则认为这个时刻收敛到了10 cm.15 cm和20 cm类推.

图1 PDOP值和卫星数目Fig.1 The PDOP value and satellite number

图2 3个方向误差Fig.2 The errors in ENU

图3 第101—107天三维误差比较Fig.3 The comparison of 3D errors during DOY 101—107
7d的收敛时间统计数据如图4和5所示.收敛时间图更加精确地反映了收敛速度.总体上讲,多系统的收敛速度一致优于单系统.在第101天至第106天中,多系统的收敛时间明显少于单系统.虽然在第107天两者在10 cm和20 cm上的收敛速度几乎相同,但是在15 cm上多系统还是要优于单系统.
综合统计7 d的数据,使用多系统的收敛时间明显少于单系统,三维误差收敛到10 cm、15 cm和20 cm需要的时间减少的平均百分比分别为42%、78%和74%.这说明多系统使用了更多的观测量,收敛速度明显加快.

图4 三维误差收敛到不同精度时所需时间比较Fig.4 The comparison of time cost for converging to di ff erent precisions

图5 收敛到不同精度时时间减少的平均百分比Fig.5 The mean percentage of time reduction for converging to di ff erent precisions
3.2 困难地区的效果比较
许多特殊用户的观测环境一般较差,比如在山区,特别是周围有高山时,可见卫星数目就会偏少,影响PPP的收敛.为此考察困难地区的PPP收敛效果,定义卫星高度截止角为35◦.
卫星数目和PDOP值的变化如图6所示.从图上可以看出,在35◦的高度截止角下, GPS系统的可见卫星数目剧烈减少,在相当长的时间内可见卫星数目低于4颗,也就是说无法实现定位;即使能够实现定位,卫星数目绝大部分也在4至5颗,相应的PDOP值也偏大.而多系统的卫星数目绝大多数情况下在6颗以上,才能够实现定位.

图6 PDOP值和卫星数目(高度截止角为35°)Fig.6 The PDOP value and satellite number(the elevation cuto ffis 35°)
3个方向的定位误差比较如图7所示.由于观测卫星较少,单系统的收敛速度非常慢,E方向收敛用了500个历元的时间,N方向收敛用了400个历元的时间,U方向收敛用了600个历元的时间.相对而言,多系统由于有较多的观测卫星,在ENU 3个方向仅分别用了50个、200个、300个历元的时间,收敛速度明显加快.此外,如果是动态定位的话,单系统由于缺少足够的观测卫星,在相当长的时间里会无法定位,这对于用户来讲是不可接受的.

图7 3个方向误差Fig.7 The errors in ENU
综上,在山区等卫星高度截止角较高的困难地区,多模卫星导航系统可以明显加快PPP的收敛,获得较好的定位结果.
4 小结
精密单点定位由于以下两个原因,其收敛时间较长:一是伪距观测量精度较低,二是卫星空间几何构型变化较慢.事实上,导致精密单点定位收敛慢的两个原因是客观存在的,也无法完全消除.所以本文从测量角度出发,考虑增加观测量个数以提高估计参数精度,进而加快PPP的收敛.增加观测量个数有两个途径,一是增加频率个数,从双频变成三频;二是增加卫星个数,使用多个卫星导航系统的数据,增加观测卫星的个数.本文采用增加观测卫星个数的途径,利用多模卫星导航系统加快PPP的收敛.
实验表明多模卫星导航系统使用了更多的观测量,收敛速度明显加快,三维误差收敛到10 cm、15 cm和20 cm需要的时间减少的平均百分比分别为42%、78%和74%.同时也表明在山区等卫星高度截止角较高的困难地区,在单一系统无法实现定位的情况下,多模卫星导航系统也可以明显加快PPP的收敛,获得较好的定位结果.
[1]Zumberge J F,He fl in M B,Je ff erson D C,et al.JGR,1997,102:5005
[2]Kouba J,H´eroux P.GPS Solutions,2001,5:12
[3]Feng Y,Gu S,Shi C,et al.Journal of Geodesy,2013,87:945
[4]Bisnath S,Gao Y.Observing our Changing Earth,2008:615
[5]Geng J.Rapid Integer Ambiguity Resolution in GPS Precise Point Positioning.Nottingham:University of Nottingham,2010:37
[6]李浩军,朱卫东,张勇.中国科学院上海天文台台刊,2013:11
[7]Geng J,Bock Y.Journal of Geodesy,2013,87:449
[8]Li P,Cai C,Santerre R,et al.Sensors,2014,14:17530
[9]Zhang X,Guo F,Li X,et al.Geomatics and Information Science of Wuhan University,2010,35:9
[10]吴玲,孙永荣,俞晓磊,等.中国空间科学技术,2009:23
[11]张勇,田林亚,徐君民,等.测绘科学技术学报,2013,30:132
[12]Anquela A B,Mart´ın A,Bern´eJ L,et al.Journal of Surveying Engineering,2012,139:47
[13]王正军.大地测量与地球动力学,2012,32:105
[14]张小红,郭斐,李星星,等.武汉大学学报:信息科学版,2010,35:9
[15]蔡昌盛,戴吾蛟,匡翠林,等.大地测量与地球动力学,2011,31:85
[16]蔡昌盛,匡翠林,戴吾蛟.测绘科学,2012,37:183
[17]蔡昌盛,朱建军,戴吾蛟,等.武汉大学学报:信息科学版,2011,36:1474
[18]蔡昌盛,戴吾蛟,匡翠林,等.武汉大学学报:信息科学版,2012,37:827
[19]Defraigne P,Baire Q.AdSpR,2011,47:265
[20]Dagoberto S,Markus B,Chen X,et al.CenterPoint RTX:Towards A Worldwide,Real-Time,Commercially Available All-GNSS Ambiguity-Fixing Precise Positioning Service.International Global Navigation Satellite Systems Society IGNSS Symposium 2013,Outrigger Gold Coast,Qld Australia,16-18 July,2013
[21]Chen X,Allison T,Cao W,et al.24thInternational Technical Meeting of the Satellite Division of the Institute of Navigation,Portland OR,19-24 September,2011:2214
Accelerating the Convergence Speed of Precise Point Positioning by Using Multi-GNSS
SONG Chao HAO Jin-ming
(School of Navigation and Aerospace Engineering,Information Engineering University, Zhengzhou 450001)
The Precise Point Positioning(PPP)does not need the support of base station,and it has broad application prospects.However,the convergence time of PPP is long.In order to accelerate the convergence speed of PPP,the PPP model using multi-GNSS(Global Navigation Satellite System)is discussed.The experiments show that the convergence speed becomes faster by using the multi-GNSS,the mean percentage of time reduction for converging to di ff erent precisions(10 cm,15 cm,and 20 cm)is 42%,78%,and 74%,respectively;meanwhile,in the severe regions,such as in the mountainous regions,the number of observed satellites becomes fewer,and the PPP sometimes cannot achieve positioning using single system.But PPP using multi-GNSS can achieve positioning and accelerate the convergence.
astrometry,earth,techniques:miscellaneous,methods:data analysis
P128;
:A
2014-11-17收到原稿,2014-12-16收到修改稿
†songchao.china@foxmail.com
‡haojm@139.com
10.15940/j.cnki.0001-5245.2015.04.006

