小行星(26)Proserpina的测光观测和建模研究∗

李 彬1,2† 赵海斌1,2 王 歆1,3

(1中国科学院紫金山天文台南京210008)

(2中国科学院行星科学重点实验室南京210008) (3中国科学院空间目标与碎片观测重点实验室南京210008)

小行星(26)Proserpina的测光观测和建模研究∗

李 彬1,2† 赵海斌1,2 王 歆1,3

(1中国科学院紫金山天文台南京210008)

(2中国科学院行星科学重点实验室南京210008) (3中国科学院空间目标与碎片观测重点实验室南京210008)

2011年12月到2012年2月期间对小行星(26)Proserpina进行了时序测光观测,获得其自转的会合周期为p=(13.107±0.002)h.结合历史测光数据,采用光变曲线凸壳反演方法对其自转状态和形状进行反演研究,并提出采用Bootstrap方法对反演参数进行误差估计.测定出(26)Proserpina是一个逆转的小行星,其极轴指向解为λ1=90.8°±1.4°, β1=−53.1°±3.2°和λ2=259.3°±2.2°,β2=−62.0°±2.0°;测定其自转的恒星周期为(13.109777±3.8×10−6)h;并基于两个极轴解反演出互为镜像的凸壳形状模型.

小行星:个别:(26)Proserpina,方法:观测,方法:数值

1 引言

概括来说,小行星亮度的变化有3种原因:(1)小行星与地球和小行星与太阳间距离的改变;(2)相位角(即从小行星看太阳和看地球两个方向间的角度)的改变;(3)小行星不规则形状以及不均匀的表面反照率在自转时所引起亮度的改变[1].

通常所说的小行星光变是指由于自转引起的光度变化,其光变周期一般是数小时.在这个期间内距离和相位角的改变都很小,因此短周期的光度变化反映了小行星的不规则形状或者表面不均匀的反照率.小行星和地球在绕日公转过程中,它们与太阳的几何位置也会发生变化,当运行到恰当位置时,地面望远镜才能观测到它们,形成可观测窗口.不同观测窗口获得的小行星光变曲线存在差异,这种差异与小行星视界角θ(自转轴与视线方向夹角)的变化有关.因此,通过积累多个观测窗口的多条光变曲线数据可反演计算出小行星的形状、自转轴指向及表面基本光学特征[2−3].

历经A(Amplitude)方法、E(Epoch)方法、AM(Amplitude-Magnitude)方法等一系列基于三轴椭球形状模型的反演方法后[4−6],Kaasalainen和Torppa等人提出基于凸壳模型的形状反演方法[2−3,7].凸壳模型比椭球模型更进一步模拟小行星的真实形状,因此该方法获得广泛的应用.例如DAMIT(Database of Asteroid Models from Inversion Techniques)小行星形状模型数据库,收集了300多个小行星凸壳反演模型[8],Hanuˇs等人通过对大量形状模型的自转参数进行统计,研究了Yarkovsky效应和YORP(Yarkovsky-O’Keefe-Radzievskii-Paddack)效应在小行星族群演化中的作用[9].

小行星(26)Proserpina是一颗典型的S型小行星,根据IRAS(Infrared Astronomical Satellite)的数据,其直径达(94.80±1.7)km.Blanco等人采用AM方法获得其自转轴指向λ1=47◦±1◦、β1=−4◦±7◦以及λ2=227◦±13◦、β2=0◦±13◦.两个轴指向都表明该小行星自转轴位于黄道面附近,但由于误差较大,难以确定小行星自转方向.轴比为a/b=1.16、b/c=1.40[10],说明这是颗扁平的小行星.

2 光变曲线观测和数据处理

国内最早进行小行星光变观测的机构是紫金山天文台,1965年张钰哲等人就使用紫金山上60 cm望远镜结合光电倍增管对(26)Proserpina进行了时序测光,这是首次获得该小行星的光变曲线[11].

2011–2012年期间,我们利用紫金山天文台盱眙观测站40 cm施密特卡塞格林式望远镜对(26)Proserpina进行了时序测光.使用的终端是加V+R滤光片的无快门U6 CCD,视场为23′×23′.由于目标星视星等很亮(V=11.4 mag),而U6 CCD没有快门,我们采用了散焦模式观测,采取了40 s和0 s交替曝光策略,用以进行相邻图像相减以消除无快门造成的星象拖尾效应,同时也达到减本底的效果.观测数据还做了暗流改正和圆顶平场改正.

此外我们还使用了Scaltriti等人的光变数据以及Pilcher用Meade 35 cm望远镜获得的光变曲线数据.用于形状反演的数据的具体信息参见表1.其中第1列是观测日期,第2列和第3列是小行星的日心距和地心距,第4列是小行星太阳相位角,第5、6列是小行星的黄经和黄纬,最后一列是数据参考文献.

3 反演方法

3.1 形状模型

Kaasalainen和Torppa等人提出的凸壳反演方法在小行星形状反演研究领域获得广泛应用.该方法在三轴椭球体模型基础上改进为凸壳模型[2−3].在假设小行星形状是凸多面体和表面反照率均匀的前提下对小行星的自转轴指向、自转周期和形状进行综合建模.使模型的光变曲线与实测光变曲线的残差最小化,即:

其中Lobs和Lmod分别表示实测光变曲线和模型光变曲线.其中模型亮度是通过散射函数S在小行星表面可见面元A+上积分得到:

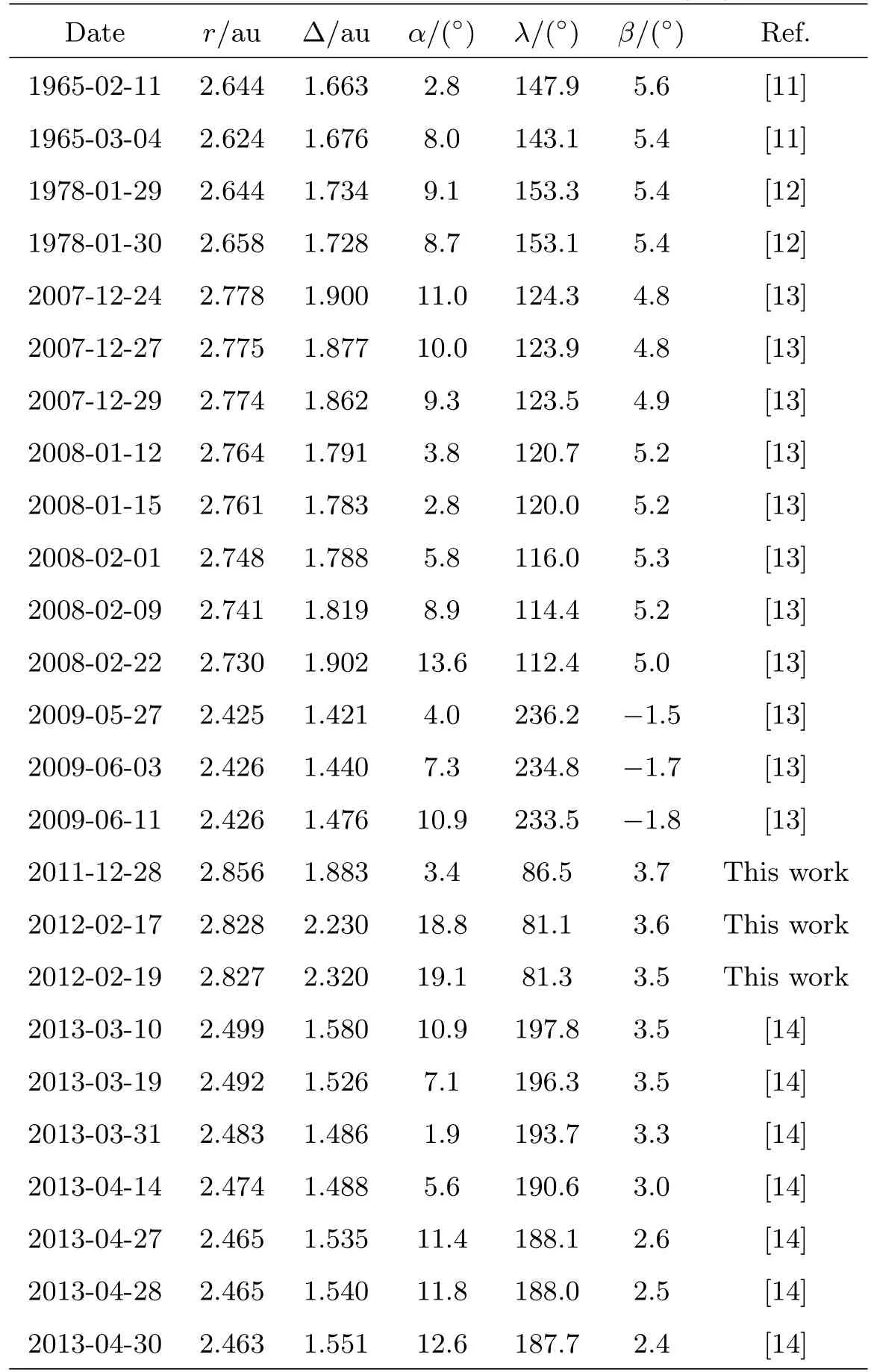
表1 (26)Proserpina的观测信息汇总表Table 1 The summary sheet of observations of(26)Proserpina

3.2 误差估计

在小行星形状反演研究中,误差估计一直是具有挑战性的工作.Kaasalainen等人认为小行星极轴指向的误差来源于散射模型和参数的不确定性,他们对于极轴指向的误差估计一般是2◦[3]到5◦[15]之间,对于恒星周期的误差估计是0.01Δp到0.1Δp之间[7],其中:

这里,p是自转会合周期,ΔT是所使用数据的时间跨度.

Kaasalainen等人对极轴指向误差估计基本是依据主观经验,2012年Wang[16]首次尝试用统计学方法进行自转状态参数的误差估计.将蒙特卡洛(Monte Carlo,MC)原理用于小行星(360)Carlova和(171)Ophelia的形状反演研究.其方法为:通过在观测的光变曲线上增加随机误差产生模拟光变曲线,再使用模拟光变曲线进行形状反演.经过多次对模拟光变曲线的反演,可以获得待测参数的分布,根据分布情况确定待测参数和参数误差.在MC模拟中,添加均值为0,标准差为0.05 mag的随机误差,对于这两个小行星的极轴误差估计在5◦左右.2014年Ansdell等人也采用该方法对小行星(3200)Phaethon进行了形状反演的误差估计.他们在观测数据上添加了µ=0,σ=0.01 mag的观测误差,对该小行星极轴的黄经和黄纬误差估计分别为13◦和10◦[17].

Wang和Ansdell等人采用的MC方法中都引入了这样一个假设:观测误差是均值为0,方差为常数的独立同分布随机量[16−17].只是在各自的MC模拟中采用了不同的方差值.而本文尝试不采用任何分布假设,仅从模型误差的独立同分布特征入手对待测参数的统计学误差估计,即采用Bootstrap方法进行误差估计.该方法最先由Efron于1979年提出,其原理是根据给定的原始样本观测信息,而不需要进行样本分布假设和增加样本信息,对总体分布特性进行统计推断的一种非参数统计方法[18].随着计算能力的提高,Bootstrap方法已经广泛应用于求估计量的方差.在天文研究领域,文献[19-22]介绍了该方法对初轨精度进行估计的研究,我们也采用这种方法对观测资料残差的重采样构成Bootstrap样本,由Bootstrap样本进行自转状态参数(自转周期、自转轴指向)的精度估计.具体过程如下所示:

(1)由原始观测数据结合光变曲线反演方法得到形状模型和自转状态参数

(3)由原始观测光变曲线和模型光变曲线计算残差:ei=L−Lod;

经过B次重复后得到一组由Bootstrap样本产生的参数,根据这组参数进行参数和参数误差估计

4 结果

4.1 自转周期初定

1965年张钰哲等人对(26)Proserpina进行了两个晚上的时序测光,拟合得到10.60 h和13.11 h的会合周期[11],最后他们采用了前者.1977–1978年Scaltriti等人测定的会合周期为13.13 h[12].此外Riccioli等人测定的会合周期为6.668 h[23],该值几乎是历史周期的一半.Ditteon等人测得的周期是(13.06±0.03)h[24].之后Fauerbach等人和Pilcher分别测定了会合周期,为(13.106±0.001)h[25]和(13.110±0.001)h[13]以及(13.109±0.001) h[14].除Riccioli的结果外,其余结果是近似的.我们使用Harris等人所提出的周期计算方法[26],对新观测数据进行周期计算,测得会合周期为(13.107±0.002)h,与前人结果吻合很好.

小行星的会合周期包含了地球公转和小行星公转的影响,恒星周期才是其真实的自转周期.因此需要结合小行星、地球和太阳的几何位置,以及自转指向和形状模型进行恒星周期拟合.在给定的周期解空间内历遍对方程(1)做最小化计算,获得一个自转周期的最优解.

根据已有的会合周期确定恒星周期的扫描范围,我们在13.106～13.120 h之间进行初步周期扫描,周期变化步长为3×10−5h.我们发现χ2最小值在13.10977 h附近.图1显示了历遍周期和对应的χ2分布情况.

图1 周期和拟合的χ2值对比Fig.1 The period vs the fi tting χ2

4.2 自转轴指向

根据光变曲线反演方法计算自转参数,需要初始自转周期和初始极轴指向.其中对于自转周期初值比较敏感,因此,采用上一步的初始周期扫描的结果.对于极轴计算,该方法将从初始极轴迭代计算出一个局部最优极轴解.因此我们将极轴解空间划分为若干个网格,然后把每个网格节点值作为极轴指向的初始值,经过迭代后找到每个节点的局部最优解,最后在所有局部最优解中找出全局最优解.

图2显示3◦×3◦网格上的历遍结果,不同颜色指示了对应极轴位置的χ2值.得到的极轴指向最优解为λ=259.3◦,β=−62.0◦,对应的恒星周期为p=13.109778 h, χ2=0.666.根据Torppa和Kaasalainen等人的研究,χ2符合(χ2−χ2min)/χ2min＜ρ,所对应的解构成比较稳定的解区间,其中ρ一般取5%或者10%[7].在历遍的结果中发现最优解的黄经方向存在一个镜像解区域,该区域的局部最优解是λ=90◦,β=−53.0◦,图1对应的p=13.109775 h,χ2=0.667.

图2 极轴解空间的χ2分布Fig.2 The distribution of χ2in the solution space of pole axis

我们采用Bootstrap方法进行1 000次模拟,取使χ2最小化的周期值和极轴值,得到由Bootstrap样本反演结果的分布.由于光变曲线和凸壳反演方法自身的局限性,无法避免在黄经方向产生镜像解(即黄经相差约180◦的解),因此Bootstrap样本的极轴解在其解空间呈现出二维双峰分布特点.在进行参数估计时,按照极轴黄经方向进行切分,以分别估计.图3显示了极轴解的分布情况,其中上面两图分别为极轴解在第1个峰值附近的黄经和黄纬的分布以及直方图;下面两幅图为极轴解在第2个峰值附近的黄经和黄纬的分布图和直方图.图中的菱形表示极轴解,直方图是极轴解在黄经和黄纬上的分布统计,曲线是对直方统计做的高斯拟合结果.极轴解分布的两个峰值分别对应的极轴P1和P2,他们互为镜像解.对极轴在黄经和黄纬方向的分布进行Gauss拟合得到分布中心和标准差.详细结果参见表2.在1 000次模拟中364次极轴解处于P1区域,636次处于P2区域.在一定程度上反映真实解所在区域的可能性.

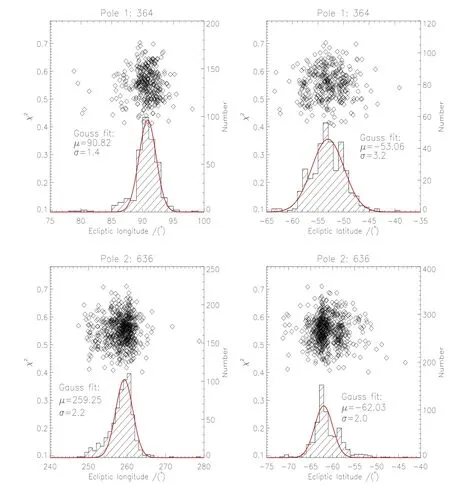
图3 Bootstrap模拟中自转参数的分布图Fig.3 The spin-parameter distributions with the Bootstrap simulation

表2 (26)Proserpina的恒星周期和极轴指向Table 2 The period and pole orientation of(26)Proserpina

4.3 形状模型

利用光变曲线反演小行星凸壳形状是光变曲线反演方法的最大特点.凸壳模型是由一系列三角面元构成的,每个面元的面积在一定程度上反映真实小行星的形状特点.

我们根据两个极轴解分别得到两个形状模型.图4的上面3个图形是第1个极轴位置的形状模型,下面是第2个极轴指向对应的形状;从左往右分别是从x轴方向、y轴方向、z轴方向观测的图形;其中z轴方向作为自转轴方向.从图形可明显看出自转轴的轴距最短,意味着(26)Proserpina是个扁平状的不规则小行星,具体的轴比信息参见表2.

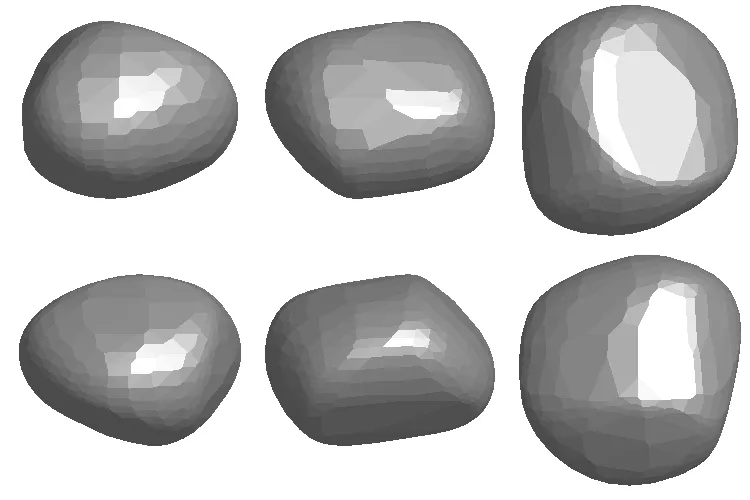
图4 (26)Proserpina的凸形状Fig.4 The convex shapes of(26)Proserpina

图5展示了我们所用的25条光变曲线和模型曲线的对照.其中α是观测时刻的太阳相位角,θ是视界角,θ0是太阳方向和小行星极轴方向的夹角,虚线表示模型曲线,黑色米字符号连成观测曲线.从图形可以看出观测曲线和模型曲线吻合得很好.

图5 观测和模型光变曲线Fig.5 The observational and modeling light curves

5 讨论与总结

我们对主带S型小行星(26)Proserpina进行光变观测并测定其自转的会合周期,使用光变曲线反演方法获得恒星周期、自转轴指向和凸壳形状模型,并采用Bootstrap方法对反演结果的不确定性进行了分析.

我们测定出该小行星的自转周期为(13.109777±3.8×10−6)h;自转轴指向为λ1= 90.8◦±1.4◦,β1=−53.1◦±3.2◦和λ2=259.3◦±2.2◦,β2=−62.0◦±2.0◦,明显偏向于南黄极,说明该小行星处于逆旋转状态.该结论与Blanco等人的结论有较大差异,这主要是由于采用的模型和方法不一样,并且我们采用了历时更长的观测数据.

从形状模型(图4)很容易看出这是个较扁平的小行星,其轴比为a/b=1.05、b/c= 1.30,表明这与Blanco等人的结论比较接近.一般情况下轴比b/c比较大,表明这可能是一个并合双星结构,或者至少在其中间有较大的凹陷区域.从形状模型看,靠近极轴区域比较平坦,很可能这就是全局大尺度的凹陷结构造成的.另一方面其不规则的光变曲线也说明这个小行星表面结构比较复杂.

基于目前的25条光变曲线,采用Bootstrap方法对形状反演进行了模拟,获得了趋于稳定的解分布.根据解的分布情况,给出了解的误差估计,误差范围从1.4◦到3.2◦之间.由于该方法不依赖于观测数据的分布模型,因此避免了分布模型的参数选择,因此可适用于小行星形状反演研究.

从光变曲线反演小行星形状本身就存在诸多不确定性因素,例如表面反照率的不均匀性,散射模型的准确度等.虽然凸壳反演方法建立的小行星形状模型比三轴椭球形状模型更接近真实形状,但由于光变数据的局限性,导致镜像难以避免.我们进行Bootstrap的模拟,取使χ2最小化的极轴解,得到解出现在P1区域的概率是0.364,出现在P2区域的概率是0.636(见图3).小行星(26)Proserpina的极轴解为P2的可能性明显高于P1.因此,就统计学意义而言,根据Bootstrap模拟可以确定极轴解的唯一性.

要进一步提高自转参数的准确性,从镜像解中区分唯一解,那么需要从反演模型和数据类型入手.例如采用结合自适应光学数据和小行星掩恒星数据的KAOLA(Knitted Occultation,Adaptive-optics,and Lightcurve Analysis)模型[27].而采用Bootstrap模拟来判断极轴唯一解也不失为一种可能,但该方法还有待更详细地研究.

[1]张钰哲,徐婉青,顾福元.天文学报,1959,7:204

[2]Kaasalainen M,Torppa J.Icar,2001,153:24

[3]Kaasalainen M,Torppa J,Muinonen K.Icar,2001,153:37

[4]Zessewitsche W.AN,1932,246:441

[5]Sather R E.AJ,1976,81:67

[6]Groeneveld L,Kuiper G P.AJ,1954,120:529

[7]Torppa J,Kaasalainen M,Michalowski T,et al.Icar,2003,164:346

[8]Durech J,Vokrouhlicky D,Kaasalainen M,et al.A&A,2008,489:L25

[9]Hanuˇs J,Durech J,Warner D,et al.A&A,2011,530:134

[10]Blanco C,Cigna M,Riccioli D.P&SS,2000,48:973

[11]张钰哲,周兴海,杨修义,等.天文学报,1981,22:169

[12]Scaltriti F,Zappala V.Icar,1979,39:124

[13]Pilcher F.MPBu,2008,35:135

[14]Pilcher F.MPBu,2013,40:189

[15]Kaasalainen M,Torppa J,Piironen J.Icar,2002,159:369

[16]Wang X B.The Shape Inversion of Asteroids and Error Estimates of Spin Parameters in Yunnan Observatory//Ip W H.New Results in the Observations and Space Exploration of Asteroids,Macao: Macau University of Science and Technology,2012:31-42

[17]Ansdell M,Meech K J,Hainaut O,et al.ApJ,2014,793:50

[18]Efron B.Annals of Statistics,1979,7:1

[19]王歆.天文学报,2013,54:73

[20]Wang X.ChA&A,2013,37:455

[21]王歆.天文学报,2013,54:274

[22]Wang X.ChA&A,2013,37:338

[23]Riccioli D,Blanco C,Cigna M.P&SS,2001,49:657

[24]Ditteon R,Hawkins S.MPBu,2007,34:59

[25]Fauerbach M,Marks S A,Lucas M P.MPBu,2008,35:44

[26]Harris A W,Youn J W,Bowell E,et al.Icar,1989,77:171

[27]Carry B,Kaasalainen M,Merline W J,et al.P&SS,2012,66:200

Photometric Observational and Modelling Study on the Asteroid(26)Proserpina

LI Bin1,2ZHAO Hai-bin1,2WANG Xin1
(1 Purple Mountain Observatory,Chinese Academy of Sciences,Nanjing 210008) (2 Key Laboratory of Planetary Sciences,Chinese Academy of Sciences,Nanjing 210008) (3 Key Laboratory of Space Object and Debris Observation,Purple Mountain Observatory,Chinese Academy of Sciences,Nanjing 210008)

We present new CCD observations of the asteroid(26)Proserpina carried out between 2011 December and 2012 February.A synodic period of(13.107±0.002) h based upon the new observations is obtained.Using all available light curves,the spin vectors,period of rotation,and the shape model of the asteroid are determined with the convex inversion method.Further more,a Bootstrap method is applied to estimate the uncertainties of the spin parameters.We derive a pair of possible poles for(26)Proserpina,and believe that it has a retrograde rotation state.The poles are determined λ1=90.8◦±1.4◦,β1= −53.1◦±3.2◦,and mirror solution of λ2= 259.3◦±2.2◦,β2=−62.0◦±2.0◦.The spin period corresponding to the two poles is almost the same as(13.109777±3.8×10−6)hours.For the asteroid,the convex shapes corresponding to the pairs of poles are mirror images of each other.

asteroids:individual:(26)Proserpina,methods:observational,methods: numerical

P185;

:A

2014-11-20收到原稿,2015-01-21收到修改稿

∗国家自然科学基金项目(11178025,11273067)、紫金山天文台小行星基金会、澳门科学技术发展基金项目(095/2013/A3)资助

†binli@pmo.ac.cn

10.15940/j.cnki.0001-5245.2015.04.004