基于冗余递减匹配的星图识别方法∗

鹿 瑶1,2,3† 张晓祥1,2 孙荣煜1,2

(1中国科学院紫金山天文台南京210008) (2中国科学院空间目标与碎片观测重点实验室南京210008) (3中国科学院大学北京100049)

基于冗余递减匹配的星图识别方法∗

鹿 瑶1,2,3† 张晓祥1,2 孙荣煜1,2

(1中国科学院紫金山天文台南京210008) (2中国科学院空间目标与碎片观测重点实验室南京210008) (3中国科学院大学北京100049)

空间目标光学观测过程中,当望远镜的指向误差与跟踪误差显著时,很难使用邻域匹配的方法完成背景恒星的配准.基于星对角距冗余递减匹配的思想,实现了一种背景恒星的高效识别方法.利用多种条件下的仿真星图以及实测图像进行了试验,结果表明,方法提高了识别成功率,且耗时少,可以准确、快速地完成星图匹配工作.

技术:图像处理,望远镜,方法:统计

1 引言

在空间目标的光学观测中,利用天文定位方法可以给出目标精度更高的赤道坐标.天文定位的关键步骤为使用定标星计算底片模型,其中首要解决的问题就是定标星的配准.定标星的配准指从星表中找出对应实际观测图像中星像的恒星,配准完成后利用多个定标星的星表赤道坐标(αi,δi)以及望远镜指向的赤道坐标(A,D),根据心射切面投影公式得到定标星的理想坐标(ξi,ηi)以及定标星的量度坐标(xi,yi),求解量度坐标到理想坐标的映射关系即得到底片常数[1].

在望远镜机架、光学系统、码盘和CCD的制造和安装过程中引入了静态指向误差[2−3],望远镜机械装置快速跟踪会造成实时指向的动态偏差[4],加上星像本身质心位置的测量误差,这些因素使得星像的量度坐标在其理想坐标的附近而非完全重合.对于理想坐标与量度坐标间偏差不显著的情况,可以用邻域匹配的方法配准定标星[5−6].然而当存在显著的指向误差与跟踪误差时,邻域匹配方法可能失效,此时需要一种不依赖量度坐标在理想坐标附近这一限制条件的匹配方法.本文采用一种模式匹配方法,利用定标星之间星对角距这种平移和旋转不变量作为基本匹配单元,可以解决量度坐标相对理想坐标有较大平移和旋转角情况下的星图配准问题.

模式匹配方法在星敏感器星图识别领域已有广泛应用[7],这些方法一类以星对角距为基础,构造简单的几何构形作为匹配模式并进行匹配,例如三角形算法[8−9]、金字塔形算法[10]等;另一类以选定的主星为匹配元,将主星周围伴星的分布特征作为匹配模式,选取相似度最高者作为匹配结果,例如栅格算法[11−12]、径向环向分布特征识别算法[13]等.

模式匹配方法已成功应用于天体测量图像的校准,如文献[14]中通过构造星四边形,生成反映4颗星相对位置的4维向量,将此向量作为匹配模式,具有平移、旋转以及比例变化下的不变性,此外文献[15]还提到了使用星四边形中三角形面积比作为模式向量.这些方法生成的模式库巨大,因此通过kd-tree方法实现快速查找,最后通过验证环节消除冗余匹配输出结果.上述方法针对天体测量图像的校准问题,其模式库相对较大,验证环节过于耗时,不利于图像的实时处理,因此对空间目标的星图配准难以适用.

当模式匹配在全天区进行时,越简单的几何构形,其相似构形越多,产生冗余匹配的可能性越大,所以星敏感器星图识别需要一定数量的参考星,这样构成的星图模式的信息维数才具有足够的分离度.对于空间目标观测,为防止长时间曝光引起星像拉长以及目标星像过曝,需要减少曝光时间,这导致实测星图极限星等降低,背景恒星数过少;此外对于小视场望远镜,在某些天区指向下,星图中背景恒星数目较少,这些情况使得上述方法难以适用.本文提出一种基于星对角距组合模式的冗余递减匹配方法,在指向误差与跟踪误差较大的情况下可以快速、准确地完成星图匹配.当背景恒星数量过少时,可以充分利用有限的特征量完成定标星配准;而当背景恒星数量足够时,提高了星图匹配效率,减少了匹配用时.

本文首先介绍了冗余递减匹配算法的思想,然后给出了算法的具体步骤,并用该方法试验了多种条件下的仿真星图以及实测图像,最后基于试验结果,分析本文方法的识别成功率、处理时间等.

2 方法描述

在指向误差与跟踪误差较大的情况下匹配星图,可以借鉴星敏感器星图识别的思想,其配准本质上是一种模式识别过程,即从模式数据库中寻找与观测图像中的模式构成最优匹配的过程.这种模式要具备两个特征:(1)模式数据库中每个元素都是唯一标识的,应具有平移和旋转不变性;(2)模式生成算法要保证同一指向下,星表生成的模式与星图中的观测模式结果尽可能一致,即对观测误差有较好的鲁棒性.

星敏感器星图识别中常用的一类方法是以星对角距为基础,构造简单的几何构形作为模式进行匹配.由于星对角距信息维数低,而星敏感器在全天范围进行星图识别,需要将角距组合成三角形、金字塔形甚至更复杂的构形来提高模式的信息维数.而在本文讨论的星图识别问题中,望远镜的先验指向信息是已知的,只需在先验指向附近、略大于望远镜视场的天区范围内生成模式数据库,其体积大大降低,减少了单个角距匹配所产生的冗余;此外,实际观测中会出现观测星图中包含背景恒星过少的情况,无法组合成复杂的几何模式进行匹配.本文提出一种冗余递减的匹配算法,逐次匹配星图中的角距,启动匹配所需的定标星数量只需两颗,同时逐渐升级匹配,减小误匹配率,匹配过程的设计也加快了匹配速度.

对于单帧观测图像,其匹配过程如下:

(1)由望远镜的先验指向、视场大小以及极限星等查找索引表,选出参考星集合,生成角距模式库,每条角距模式包括星对间角距离、相对星等差和两颗星的编号;

(2)将观测图像中背景恒星Si按测量星等由小到大排序,由S1和S2生成角距模式A12,在一定角距和星等差门限内匹配模式库中角距,取所有与之匹配的角距其两颗星的编号存入编号数组N12,其中N12的两列分别对应S1和S2的候选恒星编号.若N12内行向量唯一,即A12匹配没有冗余,认为本次匹配结束,N12内的编号即S1和S2对应恒星的编号,转入验证环节;

(3)若N12为空集,A12没有任何匹配,需要继续以其他角距作为第1条角距进行匹配;若N12行向量不唯一,A12匹配有冗余,此时判断是否存在S3,若没有则匹配失败;若存在则由S1和S3生成角距模式A13,与模式库中角距匹配得到编号数组N13,判断N13内行向量是否唯一,若唯一则S1和S3匹配完成,转入验证环节;

(4)若N13行向量不唯一,此时N12与N13均含有冗余,需要进行剔除部分冗余的“交操作”.类似于集合之间的取交集操作,N12中第1列编号与N13中第1列编号相同的行向量保留,删除两个集合中其余行向量,“交操作”后,再判断N12或N13是否存在唯一行向量,若存在则转入验证;

(5)若N12与N13仍有冗余,由S2和S3生成角距模式A23,匹配得到N23,先判断N23是否行向量唯一,若唯一则转入验证;若不唯一,N12和N23进行“交操作”,N12中第2列编号与N23中第1列编号相同的行向量保留,剔除部分冗余后再判断N12或N23是否行向量唯一,若仍有冗余,N13和N23继续进行“交操作”,再继续判断N13或N23是否行向量唯一,若某一集合行向量唯一,转入验证;

(6)若仍存在冗余,判断是否存在S4,若不存在S4,则匹配结果冗余,匹配失败;若存在,由S1和S4生成角距模式A14,匹配得到N14,若N14只含唯一行向量,则匹配完成转入验证;否则按上述步骤N14依次与N12、N13进行“交操作”;若仍存在冗余,则再加入角距A24、A34进行匹配,直到某个编号集合剔除冗余后剩下唯一行向量.若4颗星的匹配仍存在冗余,则认为本帧星图匹配失败.

(7)验证环节:若Nij匹配完成后行向量唯一,存储着与Si和Sj对应的星在星表中的编号,用两颗星的编号筛选其他所有包含Si或Sj的编号集合,得到其他星的匹配结果;也可以用这两颗定标星计算4常数底片模型,方程组如下:

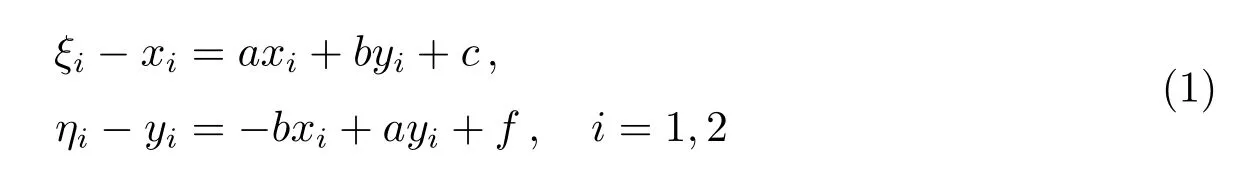
其中a、b、c、f为底片常数,(xi,yi)为图像上量度坐标,(ξi,ηi)为理想坐标,由心射切面投影公式给出:

其中(αi,δi)为投影星赤道坐标,(A,D)为投影面光心指向.对于存在冗余的星Sk,计算其所有匹配结果的理想坐标(,),i=1,2···;Sk的实测量度坐标(xk,yk)经底片模型修正后得到理想坐标(ξk,ηk),在(ξk,ηk)一定范围邻域内,若存在唯一(,),则对应的星为Sk的匹配,可以继续计算更高阶的底片常数模型;若匹配结果都没有落入此邻域,则Sk匹配失败,若图像中超过一定比例的星像匹配失败,则认为此幅图像匹配失败.

从算法流程可以看出,冗余递减匹配本质是从单一角距匹配算起,逐次加入新角距升级到三角形匹配、四边形匹配以及金字塔形匹配的过程,并在每一步都做是否唯一的判断.本文算法可行性的理论基础是,在一定天区范围内,角距库较小,特征分离度相对较大,角距单一匹配的成功概率已经很大.利用这一特征,本文算法减少了角距比较的次数,加快了匹配速度.相比于三角形匹配需要至少3颗定标星,而金字塔形匹配至少需要4颗定标星,本文算法可以处理最少两颗定标星的情况,因此提高了匹配成功率.

3 试验方法

3.1 仿真试验

根据空间目标实际观测过程中存在的问题,影响星图匹配的因素有以下4点:星像质心位置误差、星等测量误差、底片原点误差、底片指向误差.不同于传统的天体测量观测,空间目标观测一般采用大视场、跟踪式,所以空间目标图像的星像定心精度相对较差,从而给星像位置上的配准带来困难.星等在星图匹配时是可选信息,主要因为星等的测量误差往往较大,所以若选择星等为匹配信息之一时,必须考虑其测量误差的影响.底片原点误差是指底片中心指向与望远镜实时码盘读数的差异,底片指向误差指计量坐标的坐标轴与理想坐标轴存在旋转偏差[1],这两种误差的存在同样给基于先验指向的星图配准带来困难.除此之外,视场大小也是设计识别算法时需要考虑的重要因素,可以体现算法的适用性.利用计算机仿真,可以验证在这些影响因素下算法的有效性,有利于全面地评价算法性能.

仿真试验采用Tycho2星表,设置底片像素数目为1024×1024.通过计算机模拟任意指向下的观测图像,在一定范围内随机加入底片原点误差和指向误差,然后计算落入底片内的星,给底片内的星在一定范围内随机加入质心位置误差和星等测量误差,生成最终的观测图像.试验验证了在不同原点误差和指向误差、质心坐标误差和星等测量误差,以及在不同视场大小和极限星等条件下本文算法的识别率,每种情况下的识别率由蒙特-卡罗方法生成1 000幅图像的统计结果得出.

试验考查了质心位置误差和星等测量误差对识别率的影响,其中质心位置误差门限从0.5 pixel增加到3 pixel,星等误差门限分别为0.3 mag、0.5 mag、0.7 mag,误差门限t是指误差在(−t,t)之间随机产生.其他参数为视场大小7◦×7◦,极限星等为6.5 mag,指向误差门限为π/4,X、Y轴原点误差门限均为50 pixel.

试验考查了底片原点误差和指向误差对识别率的影响,原点误差门限在X、Y轴方向上从20 pixel增加到120 pixel,指向误差门限分别为π/6、π/4、π/2.其他参数为视场大小7◦×7◦,极限星等为6.5 mag,星等测量误差门限为0.7 mag,星像质心位置误差门限为3 pixel.

试验还考查了不同视场大小下本文算法的识别率,为了保证视场中观测星的数目满足匹配条件,视场大小3◦×3◦时极限星等设为8.0 mag,5◦×5◦时设为7.0 mag,7◦×7◦时设为6.5 mag,位置误差门限从0.5 pixel到3 pixel,其他设置为星等误差门限为0.5 mag,指向误差门限为π/4,原点误差门限为50 pixel.

3.2 实测试验

基于实际观测图像的试验中,使用专用于观测空间碎片的光学望远镜,随机采集多帧图像.所用望远镜的参数如表1所示.

表1 图像相关参数Table 1 The information of related images

实测图像大多为密集星场,事先通过密集星场图像配准方法给出图像中实测星像对应的星表中恒星,以验证本文算法的匹配成功率.在试验中,筛选图像上实测星等小于6.5 mag的星像作为待匹配的定标星,即变成稀疏星场下的星图匹配问题.由于实测星等存在较大误差,试验中星表极限星等设为7.0 mag,由于望远镜先验指向误差较大,为了覆盖实际视场,参考星的选取范围大小设为9◦×9◦.角距匹配阈值为10 pixel,星等差的匹配阈值为0.5 mag.采集图像时,望远镜固定地平指向,每个指向连续采集5帧图后指向下一指向.试验共采集了455帧图像,指向的赤纬跨度为−18◦至83◦,图1为一幅实测图像.

图1 一幅实测图像示意图Fig.1 An example of the surveyed picture

4 结果与讨论

4.1 仿真试验结果

质心位置误差和星等测量误差对识别率的影响如图2所示,可以看出各种情况下识别率基本在96%之上,随着位置误差增大,识别率基本呈下降趋势,这是由于增大了角距匹配门限带来更多冗余造成的;此外,本文算法的识别率对星等误差并不敏感,这是因为算法中设置了较大的星等匹配门限,虽然增加了匹配的冗余数量,但是保证了加入噪声的真实匹配能被选入候选集合,而代价是为剔除过多匹配增加了星对角距匹配量.

参考星的选取范围由指向和视场大小决定,显著的原点误差会使观测图像部分边缘区域超出参考星的选取范围,导致部分观测星无法匹配.本文算法设置了选取参考星时的视场大小略大于实际视场,确保在较大原点误差情况下,观测图像上观测星的匹配都被选入参考星集合.而角距模式具有旋转不变性,所以指向误差对模式识别影响不大.结果如图3所示,本文算法的识别率对原点误差和指向误差都不敏感.

在不同星像质心位置误差下,视场大小对识别率的影响如图4所示,3◦×3◦视场下,识别率大多达到98%以上,由于视场越小,星像质心位置精度越高,即同样像元数的位置误差对匹配的影响越小.随着视场增大,识别率有所下降,这是因为参考星越多,模式库越大,产生相似匹配的数量就越大,结果为冗余匹配的可能性越大.

根据图4中3◦×3◦对应2 pixel这一点上的识别结果,其1 000幅仿真图匹配完成所需步骤的统计结果如表2所示,其中Aij或Aij∩Ajk表示星图匹配按照上述步骤进行到Aij的匹配或Aij∩Ajk之后,得到了正确的匹配结果,对应的数值Number表示1 000幅图像中在此步骤完成匹配的星图数量.从表中可以看出,9.2%的图在第1条角距匹配后即完成匹配,说明本文算法从两颗星开始匹配的可行性,41.2%的图利用两条角距一次“交操作”即完成匹配,比三角形算法计算量要少,最多利用3颗星便可完成92.2%的星图识别,这也是算法最多升级到四星识别的原因.

图2 位置误差和星等误差对识别率的影响Fig.2 The e ff ects of position and magnitude errors on recognition rate

图3 原点误差和指向误差对识别率的影响Fig.3 The e ff ects of original and directional errors on recognition rate

图4 不同视场大小下识别率比较Fig.4 The recognition rates with di ff erent sizes of FOV

表2 仿真图像匹配完成所需步骤统计.图像视场大小3°×3°,位置噪声水平2 pixel.Table 2 The statistics of matching end o fffor the simulated pictures.The images are set as 3°×3°FOV,and within a positional error of 2 pixels.

4.2 实测试验结果

利用本文方法进行星图匹配,其中某帧图像的匹配过程如表3所示,Step表示星图匹配的进程,Set表示角距匹配结果的集合,Number表示匹配过程中集合内候选匹配的数量.可以看出,在前两步中,单个角距均无法完成匹配,依次进行“交操作”之后,候选星集合冗余数量大大减少,随着更多的角距加入匹配中,所有匹配集合的冗余数量逐步减少.当A12∩A14之后,两条角距对应的候选星编号集合N12、N14都只剩唯一匹配,即A12、A14已找到匹配,最后经过验证环节,所有角距都完成了匹配.

实测图像中至少有2颗定标星的图像共428幅,应用本文方法成功匹配406幅,成功率为94.9%,所有匹配失败均是因为匹配结果有冗余,原因是图像中定标星不足.其中27%的失败图像只含3颗定标星,升级到三角形算法时仍然无法剔除冗余,其余73%的失败图像则只有2颗定标星,更加难以识别.在所有只含2颗定标星的实测图像中,匹配成功率只有11.1%,若参考三角形算法以至少有3颗定标星的图像统计,则410幅图像中成功匹配404幅,成功率为98.5%.失败匹配是由只含3颗定标星的图像匹配冗余所致,在所有只含3颗定标星的实测图像中,匹配成功率为81.25%.可以看出只含很少定标星的极端图像是造成识别率下降的主要原因,实际工作中实时处理数据时,对于少量无法匹配的图像可以保存下来用其他方法再处理.

每幅图像完成识别所使用的匹配步骤可以反映算法的计算量,按上一节设定的初始门限,统计在某个步骤完成匹配的图像数量如表4中第2列数据所示,其中6.3%的图仅使用第1条角距即完成匹配,比相同视场下仿真结果9.2%低,还是因为设置了较宽门限,40.4%的图只利用两条角距就完成了匹配,在升级到三角形算法时可完成86.2%的星图匹配,升级到四边形算法时,匹配率已经达到94.9%,而金字塔形算法没有完成任何对仍然冗余图像的匹配,每幅图平均的角距匹配次数为2.6次.在后续试验中,适当减小星等差和角距匹配门限,可以减少每步产生的冗余加快匹配进程,这需要对图像的质心位置误差和星等测量误差有较准确的先验估计,或者利用迭代处理的方法给出适当的星等差和角距门限,然后再匹配星图.改进角距门限为6 pixel,星等差门限为0.3 mag,匹配统计结果如表4中第3列所示,此时每幅图平均的角距匹配次数为2.1次,匹配速度大大加快.

星图匹配耗时最主要来自角距匹配过程,因为每一次角距匹配都需要遍历角距库,利用本文方法匹配实测图像,每幅图平均的角距匹配次数小于3次,要优于三角形算法和四边形算法.与三角形算法类似,还可以利用k-vector方法加快角距检索速度.图5是实测图像在初始门限下每幅图的匹配耗时,所用机器为HP台式机,处理器为intel core2,使用C++编程计算,可以看出绝大多数图像匹配时间在50 ms以下,表明本文方法耗时少,有利于数据的实时处理.

表3 某幅实测图像的匹配过程Table 3 An example of matching process for one surveyed picture

图5 匹配过程时间消耗Fig.5 The time costing for matching process

表4 实测图像匹配完成所需步骤统计Table 4 The statistics of matching end o fffor the surveyed pictures

5 结论

在望远镜指向误差与跟踪误差较大时,传统邻域匹配方法很难完成背景恒星的配准工作.本文提出了一种基于角距匹配的冗余递减算法,从单个角距逐渐组合成复杂模式,该方法利用匹配特征的平移和旋转不变性,可以克服原点误差和指向误差的影响.本文算法简单易实现,在偏差较大时,高效、准确地实现了星图识别.由于问题的相似性,本文算法对星敏感器星图匹配同样适用.通过仿真星图和实测星图的试验结果可以发现,本文算法星图匹配成功率较高,同时匹配过程运算量比传统三角形算法少,可以满足星图处理实时性的要求.

[1]李东明,金文敬,夏一飞,等.天体测量方法.北京:中国科学技术出版社,2006:70-91

[2]张晓祥,吴连大.天文学报,2001,42:198

[3]平一鼎,张晓祥,鲁春林.天文学报,2006,47:224

[4]张晓祥,吴连大,鲁春林.天文学报,2003,44:65

[5]孙荣煜,张晓祥,赵长印.天文学报,2013,54:168

[6]Sun R Y,Zhang X X,Zhao C Y.ChA&A,2013,37:464

[7]Padgett C,Kreutz D K,Udomkesmalee S.JGCD,1997,20:259

[8]Cole C L,Crassidis J L.JGCD,2006,29:64

[9]Mortari D,Neta B.K-vector Range Searching Techniques.Paper AAS 00-128 of the 10th Annual AIAA/AAS Space Flight Mechanics Meeting,Clearwaters,January 23-26,2000

[10]Mortari D,Samaan M A,Bruccoleri C,et al.Navig,2004,51:171

[11]Padgett C,Kreutz D K.ITAES,1997,33:202

[12]Na M,Zheng D N,Jia P F.ITAES,2009,45:516

[13]Zhang G J,Wei X G,Jiang J.Image and Vision Computing,2008,26:891

[14]Dustin L,David W H,Keir M.AJ,2010,139:1782

[15]Jeremy S H.MNRAS,2013,433:935

A Star Recognition Method with Decreasing Redundancy Matching

LU Yao1,2,3ZHANG Xiao-xiang1,2SUN Rong-yu1,2
(1 Purple Mountain Observatory,Chinese Academy of Sciences,Nanjing 210008) (2 Key Laboratory of Space Object and Debris Observation,Chinese Academy of Sciences,Nanjing 210008) (3 University of Chinese Academy of Sciences,Beijing 100049)

During the optical observations of space objects,it is difficult to enable the background stars to get matched when the telescope pointing error and tracking error are striking.Depending on the idea of decreasing redundancy matching,an efficient recognition method for background stars is proposed in this paper.The simulation stellar pictures in di ff erent conditions and the surveyed stellar pictures are used to verify the proposed method.The experimental results show that the proposed method performs a higher rate of recognition and less time costing,and it is able to match stellar pictures accurately and rapidly.

techniques:image processing,telescopes,methods:statistical

P123;

:A

2014-12-12收到原稿,2015-02-11收到修改稿

∗国家自然科学基金项目(11273069,11403108)资助†luyao@pmo.ac.cn

10.15940/j.cnki.0001-5245.2015.04.010