H(z)数据对相互作用暗能量模型的观测研究∗

潘 宇1,2 李 力1 曹 硕3 潘娜娜1,2† 张 益1,2 胡紫萱1

(1重庆邮电大学理学院重庆400065) (2中国科学院理论物理研究所理论物理国家重点实验室北京100190) (3北京师范大学天文系北京100875)

H(z)数据对相互作用暗能量模型的观测研究∗

潘 宇1,2 李 力1 曹 硕3 潘娜娜1,2† 张 益1,2 胡紫萱1

(1重庆邮电大学理学院重庆400065) (2中国科学院理论物理研究所理论物理国家重点实验室北京100190) (3北京师范大学天文系北京100875)

结合最新的哈勃参量H(z)观测数据、重子声学振荡(BAO)数据与普朗克卫星观测得到的宇宙微波背景辐射(CMB)数据,利用马尔柯夫链蒙特卡洛算法(MCMC)对一种相互作用暗能量模型进行了观测限制.这3种数据联合限制得到的各参数的最佳拟合值及1σ误差范围分别为:物质能量密度参数Ωm=相互作用因子γ=暗能量状态方程参数wX=哈勃常数H0=相互作用耦合参数γ＞ 0表明能量正在从暗物质转移到暗能量.然而,宇宙学常数模型中的巧合性问题在1σ误差范围内依然可以轻微缓解.为了更好地做出比较,还利用BAO+CMB组合数据及单独的H(z)数据对该模型进行了考察,得到的结果如下: (1)H(z)数据能对相互作用参数γ给出更好的限制结果;(2)ΛCDM模型仍然是与观测数据符合得最好的模型,耦合参数γ与其它模型参数(Ωm,H0)相互关联;(3)在考虑了暗能量与暗物质间的相互作用之后,超新星局域距离阶梯测量与普朗克观测对H0限制结果的冲突问题能够得到一定程度的缓解.

宇宙学:暗能量,宇宙学:宇宙学参数,宇宙学:观测

1 引言

近年来,各种天文观测结果已经证实我们所处的宇宙正处于一个加速膨胀的时期[1−13].为了解释这种不可思议的现象,人们考虑宇宙中可能存在着一种具有负压强的暗能量,它均匀地分布在整个宇宙空间并且主导着宇宙的加速膨胀.最简单的暗能量模型是基于广义相对论而提出的ΛCDM模型,该模型能够很好地解释各种观测数据,但却存在着颇受争议的巧合性问题:由理论可知,宇宙中的物质密度随着宇宙膨胀以a−3衰减(a为标度因子,a=(1+z)−1,其中z代表红移),而作为暗能量的宇宙学常数Λ的密度不会发生改变,但是为什么现在我们所处时期的暗能量与物质的密度具有相同的量级?为了有效地解释和缓解这个问题,各种暗能量动力学模型相继被提出,包括精质模型(Quintessence)[14−15]、幽灵暗能量模型(Phantom暗能量)[16−17]、k-essence模型[18−19]、精灵模型(Quintom暗能量)[20−22]等.此外,更为有效的一种方法是考虑暗能量和暗物质之间可能存在相互作用,本文将聚焦一种重要的相互作用暗能量模型.该模型采用一种简单的唯象方法来描述宇宙中暗能量与物质组分的演化,即暗能量与物质密度之比正比于尺度因子的幂指数形式.此外,对于研究宇宙目前的加速膨胀过程,借助天文观测数据对暗能量模型进行观测检验是一种非常重要的手段.众所周知,诸如伽玛暴(GRBs)[23−24]、Ia型超新星(SNe Ia)、重子声学振荡(BAO)、宇宙微波背景辐射(CMB)等观测数据使用的都是对距离来进行测量.比如,限制暗能量模型参数最常用的方法是将这些参数与光度距离拟合:

本文主要由以下几部分组成:在第2部分中我们将主要介绍暗能量与暗物质相互作用模型的理论框架,第3部分则主要介绍各种天文观测数据,第4部分将对暗能量模型的限制结果进行分析与讨论,最后对本文得到的结论进行简要总结.

2 相互作用暗能量模型

为了缓和巧合性问题,一个很好的方法就是考虑暗能量和暗物质之间可能的相互作用.我们通常假定它们之间仅通过引力耦合来进行能量交换.例如,暗能量可能会受到诸如黑洞等天体的引力作用而被大质量致密天体吸积.而在宇宙学背景下,微弱但不能被忽略的能量会在暗能量与暗物质之间进行转移.人们已经发现恰当的相互作用会影响摄动动力学和CMB角功率谱的最低阶多极矩[35−37].因此,我们可以通过宇宙的膨胀历史来推断出暗能量与暗物质之间的相互作用.

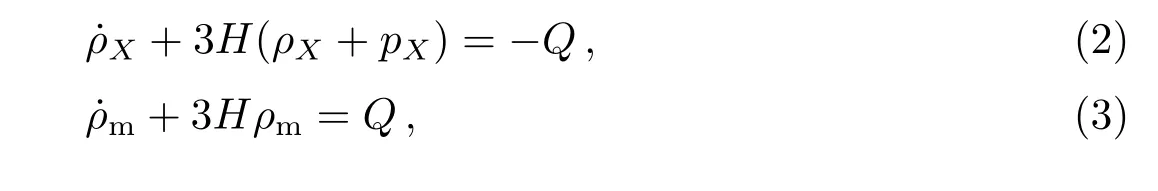
在平坦的FRW度规描述的宇宙中,暗物质和暗能量并非独立演化,两者可以通过相互作用项Q进行能量交换:此时能量守恒方程tot+3H(ρtot+ptot)=0依然适用,其中ρtot=ρX+ρm.由于暗能量与暗物质的未知性,我们很难从第一性的原理出发计算出两者之间相互作用的形式.通过唯象描述的方法,之前诸多文献在Q的参数化形式方面做出了很多工作[38−50].在本文中,我们将引入一个新的参数来刻画相互作用项,即假设暗能量和物质密度之比正比于标度因子的幂指数形式:数[52].此时相互作用项Q的表达式为[26,47,51]:其中ξ是量化巧合性问题严重程度的常数参

其中Ωm是当前宇宙中的物质密度参数,γ=ξ+3wX为相互作用因子.γ=0代表暗能量与暗物质间不存在相互作用的标准宇宙学模型,而γ̸=0则表示存在能量交换的非标准宇宙学模型.此外,当γ＞0时,能量的转移方向是从暗物质到暗能量(Q＜0),巧合性问题依然非常严重,而γ＜0恰恰相反(Q＞0).此外,本文中将假设暗能量的状态方程wX≡pX/ρX在平直的FRW度规中为一个常数参数,此时的弗雷德曼方程可表示为

3 哈勃参量H(z)以及其他观测数据

与其他各种距离测量数据不同,哈勃参数取决于宇宙年龄相对于红移的变化率[53]

因此,如果可以对dz/dt进行精确测量,就可以直接得到红移z处的哈勃参量H(z)值.目前H(z)数据可以通过两种观测方法得到,一种是测量不同红移处的Red-envelope星系的年龄,另外一种则是从重子声学振荡峰值的观测中分析提取H(z).这就是大家熟知的“年龄差分法(Di ff erential Age Method)”和“峰值法(Peak Method)”.本文将使用结合以上两种测量方法得到的最新31组H(z)数据.其中,11组不同红移的数据来自文献[54], 2组来源于文献[55],8组出自于文献[56],3组来源于文献[57],4组源于文献[58],剩余3组出自于文献[59-61].我们将采用χ2检验的方法对各个宇宙学参数进行检验和限制,哈勃参量数据对应的χ2值如下

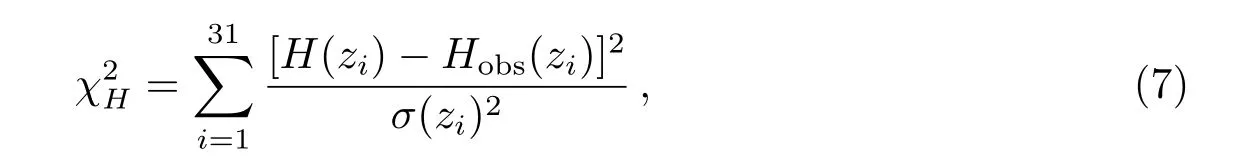
其中H(zi)、Hobs(zi)和σ(zi)分别代表H(z)的理论值、观测值和相应的1σ误差.

对于重子声学振荡观测数据,我们首先考虑由亮红星系(Luminous Red Galaxies)巡天7 yr数据(Data Release 7)发布的测光样本得到的BAO角标度:θBAO(z=0.55)= (3.90±0.38)◦[62−64].该数据是对单纯的角重子声学振荡信号的首次直接测量.θBAO定义为[65]

其中依赖模型的共动径向距离Dr(z)表示为:

声速视界rs(z)为：

对于宇宙微波背景辐射观测,采用普朗克卫星最新得到的包括声学尺度la、偏移参数R及Ωbh2在内的数据[31−32].此时H(z)+BAO+CMB联合数据给出的χ2值可表示为:

4 模型参数拟合结果

利用上述最新的观测结果,将采用基于马尔柯夫链蒙特卡洛(MCMC)算法的最大似然法[67]拟合相应的χ2值.H(z)+BAO+CMB联合数据给出的模型最佳拟合值及1σ的误差为:Ωm=以及H0值得注意的是,相互作用因子γ的最佳拟合值非常小,这表明暗能量与物质间的相互作用强度非常弱;其次,γ＞0表明能量正从暗物质向暗能量转化.

作为对比,我们分别用H(z)和BAO+CMB两种数据组合限制了相互作用模型参数,得到的结果见图1-3和表1.拟合结果显示:虽然单独的H(z)数据不能很好地限制模型参数,但是H(z)+BAO+CMB所得结果比BAO+CMB限制得更好.这表明,H(z)数据能够更好地限制模型参数以及减小γ.并且,通过对比之前H(z)样本与H(z)+BAO+CMB数据限制结果[26],本文得到的限制结果误差更小.由图1-3可知,模型参数γ、Ωm、H0三者间存在相互关联的可能性.此外,由表1可知,单独使用哈勃参量H(z)数据得到的相互作用因子γ＜0,这与其它两种数据组合下的结论相反.同时,γ=0在1σ置信区间内依然与观测数据相符,这与之前人们所得的结论符合得很好[26,47,68].在图4中,我们还比较了31组哈勃参量的测量值与相互作用暗能量模型中哈勃参数随红移演化的理论曲线,结果表明:模型框架下的H(z)随红移z的演化与观测结果符合得很好.

众所周知,基于ΛCDM模型,普朗克卫星和超新星观测数据给出的哈勃常数H0值存在明显的不一致.普朗克卫星给出的H0=(67.3±1.2)km·s-1·Mpc-1,而超新星局域距离阶梯测量给出的H0=(73.8±2.4)km·s-1·Mpc-1[69−70].通过比较本文H(z)和BAO+CMB得到的结果,我们发现在1σ范围内两种数据给出的H0拟合结果精度相同且符合度很高.并且考虑相互作用项后所得的H0与普朗克及超新星给出的结果都符合很好,这表明:引入了相互作用项后的暗能量模型可以较好地缓解这两种数据给出的哈勃常数拟合结果的不一致性.

图1 由H(z)(点划线)、BAO+CMB(点线)和H(z)+BAO+CMB(实线)数据组合得到的Ωm与γ参数1σ和2σ误差等高线图,其中菱形、星形与十字分别对应于H(z)、BAO+CMB和H(z)+BAO+CMB数据组合下的最佳拟合值Fig.1 The marginalized 1σ and 2σ con fi dence contours of the parameters Ωmand γ in the phenomenological interacting scenario,obtained from the combinations of all observational data H(z) (dash-dotted line),BAO+CMB(dotted line),and H(z)+BAO+CMB(solid line),where the diamond, star,and cross are the best- fi t values for the observational data H(z),BAO+CMB,and H(z)+BAO+CMB,respectively

图2 由H(z)(点划线)、BAO+CMB(点线)和H(z)+BAO+CMB(实线)数据组合得到的γ与H0参数1σ和2σ误差等高线图,其中菱形、星形与十字分别对应于H(z)、BAO+CMB和H(z)+BAO+CMB数据组合下的最佳拟合值Fig.2 The marginalized 1σ and 2σ con fi dence contours of the parameters γ and H0in the phenomenological interacting scenario,obtained from the combinations of all observational data H(z) (dash-dotted line),BAO+CMB(dotted line),and H(z)+BAO+CMB(solid line),where the diamond, star,and cross are the best- fi t values for the observational data H(z),BAO+CMB,and H(z)+BAO+CMB,respectively

图3 由H(z)(点划线)、BAO+CMB(点线)和H(z)+BAO+CMB(实线)数据组合得到的Ωm与H0参数的1σ和2σ误差等高线图,其中菱形、星形与十字分别对应于H(z)、BAO+CMB和H(z)+BAO+CMB数据组合下的最佳拟合值Fig.3 The marginalized 1σ and 2σ con fi dence contours of the parameters Ωmand H0in the phenomenological interacting scenario,obtained from the combinations of all observational data H(z) (dash-dotted line),BAO+CMB(dotted line),and H(z)+BAO+CMB(solid line),where the diamond, star,and cross are the best- fi t values for the observational data H(z),BAO+CMB,and H(z)+BAO+CMB,respectively

图4 相互作用暗能量模型中H(z)随红移的演化图(实线).误差棒代表31个哈勃参数观测值,模型参数来自H(z)+BAO+CMB数据组合得到的最佳拟合值.Fig.4 The evolution of H(z)as a function of z in the interaction dark energy model(solid line).The error bars are the 31 Hubble parameter measurements,and the model parameters are taken as the best- fi t values from H(z)+BAO+CMB.

表1 使用H(z)、BAO+CMB和H(z)+BAO+CMB数据组合对相互作用暗能量模型拟合得到的γ、wX、Ωm和H0参数及1σ误差Table 1 The marginalized 1σ errors of the parameters γ,wX,Ωm,and H0for the phenomenological interacting dark energy scenario,obtained from H(z), BAO+CMB,and H(z)+BAO+CMB combinations,respectively

5 结论

在本文中,我们结合最新的哈勃参量H(z)观测数据、重子声学振荡(BAO)数据、普朗克卫星观测得到的宇宙微波背景辐射(CMB)数据,利用马尔可夫链蒙特卡洛算法对一种相互作用暗能量模型进行了观测研究.首先,从H(z)+BAO+CMB组合得到的相互作用耦合参数可知,虽然最佳拟合值支持能量由暗物质向暗能量转移的可能性,但巧合性问题在1σ误差范围内依然可以得到轻微缓解.其次,我们发现:不同数据组合限制下得到的模型拟合结果吻合得很好,引入哈勃参量观测数据可以显著改善对模型参数的限制结果.在相互作用暗能量模型的理论框架下,观测数据得到的结果表明γ、Ωm和H0三者相互关联,并且在1σ置信范围内ΛCDM模型仍然与观测数据符合得很好.最后,分析结果显示:在考虑了暗能量与物质之间的相互作用之后,Ia型超新星数据和普朗克数据间对于哈勃常数H0拟合结果的不一致性得到了一定程度的缓解.

[1]Riess A G,Filippenko A V,Challis P,et al.AJ,1998,116:1009

[2]Perlmutter S,Aldering G,Goldhaber G,et al.ApJ,1999,517:565

[3]Spergel D N,Verde L,Peiris H V,et al.ApJS,2003,148:175

[4]Tegmark M,Blanton M R,Strauss M A,et al.ApJ,2004,606:702

[5]Eisenstein D J,Zehavi I,Hogg D W,et al.ApJ,2005,633:560

[6]Astier P,Guy J,Regnault N,et al.A&A,2006,447:31

[7]Spergel D N,Bean R,Dor´e O,et al.ApJS,2007,170:377

[8]Komatsu E,Dunkley J,Nolta M R,et al.ApJS,2009,180:330

[9]Amanullah R,Lidman C,Rubin D,et al.ApJ,2010,716:712

[10]Cao S,Zhu Z H.SCPMA,2011,54:2260

[11]Cao S,Covone G,Zhu Z H.ApJ,2012,755:31

[12]Cao S,Pan Y,Biesiada M,et al.JCAP,2012,03:016

[13]Gong Y G,Gao Q,Zhu Z H.MNRAS,2013,430:3142

[14]Ratra B,Peebles P J E.PRD,1988,37:3406

[15]Caldwell R R,Dave R,Steinhardt P J.PRL,1998,80:1582

[16]Caldwell R R.PLB,2002,545:23

[17]Caldwell R R,Kamionkowski M,Weinberg N N.PRL,2003,91:071301

[18]Armendariz-Picon C,Mukhanov V,Steinhardt P J.PRD,2001,63:103510

[19]Chiba T.PRD,2002,66:063514

[20]Feng B,Wang X L,Zhang X M.PLB,2005,607:35

[21]Guo Z K,Piao Y S,Zhang X M,et al.PLB,2005,608:177

[22]Feng B,Li M Z,Piao Y S,et al.PLB,2006,634:101

[23]刘建炜,王发印.天文学报,2011,52:467

[24]Liu J W,Wang F Y.ChA&A,2011,36:155

[25]Wei H,Cai R G.PRD,2006,73:083002

[26]Cao S,Liang N,Zhu Z H.MNRAS,2011,416:1099

[27]Liao K,Li Z,Ming J,et al.PLB,2013,718:1166

[28]Farooq O,Mania D,Ratra B.ApJ,2013,764:138

[29]Adak D,Majumdar D,Pal S.MNRAS,2014,437:831

[30]Gong Y G,Gao Q.EPJC,2014,74:2729

[31]Ade P A R,Aghanim N,Armitage-Caplan C,et al.A&A,2014,571:16

[32]Wang Y,Wang S.PRD,2013,88:043522

[33]Percival W J,Reid B A,Eisenstein D J,et al.MNRAS,2010,401:2148

[34]Blake C,Kazin E A,Beutler F,et al.MNRAS,2011,418:1707

[35]Wang B,Gong Y G,Abdalla E.PLB,2005,624:141

[36]Wang B,Zang J D,Lin C Y,et al.NuPhB,2007,778:69

[37]Rozas-Fern´andez A,Brizuela D,Cruz N.IJMPD,2010,19:573

[38]Copeland E J,Liddle A R,Wands D.PRD,1998,57:4686

[39]Amendola L.PRD,1999,60:043501

[40]Cai R G,Wang A Z.JCAP,2005,03:002

[41]Wei H,Cai R G,Zeng D F.CQGra,2005,22:3189

[42]Guo Z K,Zhang Y Z.PRD,2005,71:023501

[43]Wei H,Cai R G.PRD,2005,71:043504

[44]Wang B,Lin C Y,Abdalla E.PLB,2006,637:357

[45]Wei H,Cai R G.PLB,2006,634:9

[46]Wei H,Cai R G.JCAP,2007,09:015

[47]Guo Z K,Ohta N,Tsujikawa S.PRD,2007,76:023508

[48]Chen X M,Wang B,Pan N N,et al.PLB,2011,695:30

[49]Pan Y,Cao S,Gong Y G,et al.PLB,2013,718:699

[50]Cao S,Liang N.IJMPD,2013,22:1350082

[51]Dalal N,Abazajian K,Jenkins E,et al.PRL,2001,87:141302

[52]Pavon D,Sen S,Zimdahl W.JCAP,2004,05:009

[53]Jimenez R,Verde L,Treu T,et al.ApJ,2003,593:622

[54]Stern D,Jimenez R,Verde L,et al.JCAP,2010,02:008

[55]Gazta˜naga E,Cabr´e A,Hui L.MNRAS,2009,399:1663

[56]Moresco M,Cimatti A,Jimenez R,et al.JCAP,2012,08:006

[57]Blake C,Brough S,Colless M,et al.MNRAS,2012,425:405

[58]Zhang C,Zhang H,Yuan S,et al.RAA,2014,14:1221

[59]Anderson L,Eric A,Stephen B,et al.MNRAS,2014,439:83

[60]Busca N G,Delubac T,Rich J,et al.A&A,2013,552:18

[61]Chuang C H,Wang Y.MNRAS,2013,435:255

[62]Crocce M,Gaztanaga E,Cabre A,et al.MNRAS,2011,417:2577

[63]Carnero A,Sanchez E,Crocce M,et al.MNRAS,2012,419:1689

[64]Liao K,Pan Y,Zhu Z H.RAA,2013,13:2

[65]S´anchez E,Carnero A,Garc´ıa-Bellido J,et al.MNRAS,2011,411:277

[66]Eisenstein D J,Hu W.ApJ,1998,496:605

[67]Lewis A,Bridle S.PRD,2002,66:103511

[68]Chen Y,Zhu Z H,Alcaniz J S,et al.ApJ,2010,711:439

[69]Riess A G,Macri L,Casertano S,et al.ApJ,2011,730:119

[70]Freedman W L,Madore B F,Scowcroft V,et al.ApJ,2012,758:24

Testing the Interaction Dark Energy Model with H(z) Data

PAN Yu1,2LI Li1CAO Shuo3PAN Na-na1,2ZHANG Yi1,2HU Zi-xuan1
(1 College of Science,Chongqing University of Posts and Telecommunications,Chongqing 400065) (2 State Key Laboratory of Theoretical Physics,Institute of Theoretical Physics,Chinese Academy of Sciences,Beijing 100190) (3 Department of Astronomy,Beijing Normal University,Beijing 100875)

We constrain an interaction dark energy model with the newly revised H(z) data combining with the 7-year baryon acoustic oscillation(BAO)data and the cosmic microwave background(CMB)observations from the Planck fi rst data release using the Markov Chain Monte Carlo(MCMC)method.The marginalized 1σ constraints of the combinations:Ωm=and H0=The coupling parameter is γ＞0 which means the energy is transferred from dark matter to dark energy,and the coincidence problem is slightly alleviated in 1σ range.For comparison,we constrain this model with BAO+CMB observations and H(z)data alone.The results are as follows:(1)The H(z)data could put stricter constraint on the parameter γ.(2)The ΛCDM model remains the best, and the coupling parameter γ is correlated with other model parameters Ωmand H0. (3)The tension of the constraining results of H0between the local distance ladder measurements and the Planck result could be alleviated by considering the interaction term.

cosmology:dark energy,cosmology:cosmological parameters,cosmology: observations

P159;

A

2015-03-11收到原稿,2015-03-23收到修改稿

∗国家自然科学基金项目(11005164,11447213)、重庆市教育委员会科学技术研究项目(KJ130535)、重庆邮电大学科学研究基金(A2013-25,A2014-43)、中央高校基本科研业务费专项资金以及中国博士后科学基金面上资助项目(2014M550642)资助

†pannn@cqupt.edu.cn

10.15940/j.cnki.0001-5245.2015.04.001