对比教学法在微积分教学中的应用

张艳霞

(安徽工业大学 数理学院，马鞍山 安徽 243002)



对比教学法在微积分教学中的应用

张艳霞

(安徽工业大学 数理学院，马鞍山 安徽 243002)

在高等数学微积分教学中，使用对比教学法提出问题，分析问题,概括、总结知识等，不仅有助于学生对知识的记忆、理解，更能培养学生发现、分析和解决问题的能力。

微积分；对比教学法；创新思维

概念、定理、公式多而抽象是高等数学的突出特点，许多学生学习起来感觉比较吃力。怎样才能让学生更好地理解、记忆并应用这些复杂的概念、定理、公式，使数学变得易懂易记易用是数学教师面临的一大难题。在几年的教学实践中笔者体会到对比教学法对解决这一问题有很大帮助。在教学过程中，将相互区别又相互联系的内容放在一起，引导学生通过对比的方法由表及里地认识所学内容，概括总结出知识点之间的相同之处与本质区别，可加深学生对所学知识的深刻理解，并能记住所学内容。下面介绍本人在教学过程中的一些体会。

一 、利用对比提出问题，分析问题

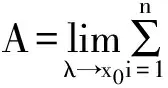
二、利用对比进行概括、总结

对学过的内容进行概括总结是学习的一个重要的，必不可少的环节，有利于学生对所学过的内容加深理解和记忆。在一章内容或一篇内容学过之后要及时引导学生，用对比的方法进行概括、总结，有利于培养学生的逻辑思维能力。比如当导数和微分这一章学完后，就可以利用对比总结，概括，比较它们的相同点和不同点。如比较一元函数的导数和多元函数的偏导数，它们都是利用极限来定义，一元函数的导数是函数增量与自变量增量商的极限。多元函数偏导数是偏增量与自变量增量商的极限。形式上虽有所不同，但本质上多元函数偏导是把其他变量固定后的一元函数导数。一元函数的导数几何意义是平面曲线上对应点切线的斜率，多元函数的偏数几何意义是某个空间曲线上对应点切线相对于某个坐标轴的斜率。但是对一元函数来讲可导肯定连续，对多元函数来讲(以二元函数为例)，两个偏导数都存在却不一定连续，这里可以给学生举出一个实例，例如：

在(0，0)点两个偏导都存在，但是该函数在(0，0)点却不连续。

再来比较微分，一元函数微分dy=f＇(x)dx和二元函数全微分dz=fx(x)dx+fy(x)dy在形式类似。在求法上可以直接代公式，也可以用微分形似不变性。当然他们之间也有区别：一元函数可导一定可微，二元函数两个偏导都存在却不一定可微，例如：

在(0,0)点两个偏导都存在，但是该函数在(0,0)点却不可微。

经过这样的比较，学生对一元函数连续、导数、微分与二元函数连续、偏导、全微分会有深刻的理解，而且把前后所学的东西都串在一起，形成一个整体有利于学生记忆这些内容，能达到事半功倍的效果 ，也能够激发学生的兴趣，消除学生的恐惧心理。

在讲解两类曲线积分，两类曲面积分时更是要引导学生比较它们的区别与联系，首先是物理背景不同，然后是计算方法不同。两类曲线积分可以相互转化，两类曲面积分也可以相互转化，让学生列举出来，这样能加深对概念的理解，计算时才不会出错。

三、结语

在微积分教学中恰当使用对比教学法不仅有助于学生对已学知识的记忆，也有利于学生对新学知识的理解，更能培养学生发现、分析和解决问题的能力，调动学习积极性，提高学习兴趣，激发学生的创造意识，从而培养创新能力。

[1]刘景麟,黄振友.微积分[M].北京:国防工业出版社, 2006.

[2]汪志宏.高等数学教学中对比式教学法的应用探析[J]. 科教文汇,2012(上旬刊)：100-106.

[3]王利平.浅谈高等数学教学中的概念引入模式[J]. 数学理论与应用, 2005(4):143-144.

[4]毛京中. 高等数学概念教学的一些思考[J]. 数学教育学报, 2003(2):83-86.

(责任编辑 雷金火)

The Application of Comparative Teaching Method in the Teaching of Calculus

ZHANG Yan-xia

(Mathematical Institute, Anhui University of technology, Ma’anshan 243002, Anhui, China)

In the teaching of advanced mathematics of calculus, using comparative teaching method to raise questions, analyze, summarize knowledge will be helpful with students’ memory and understanding of knowledge. It can cultivate students’ ability to discover, analyze, and solve problems.

Calculus; comparative teaching method; innovative thinking

2014-11-10

安徽工业大学校级质量工程项目(RC14200005)

张艳霞(1980-)，女，山东邹城人，安徽工业大学数理学院副教授，硕士。

G642.4

A

1671-9247(2015)04-0113-02