例谈初中数学教学中的一题多解

广东省梅州市梅县区宪梓中学 许素芬

一、教师在教学中进行“一题多解”训练的意义

通过十多年的初中数学教学，我觉得一些数学题用几种方法都能解决。只有平时多讲解和总结，才能锻炼学生思维的灵活性，活跃思路，根据题目给出的已知条件，结合自身情况，不满足仅仅得出一道习题的答案，而去追求更独特、更快捷的解题方法；才能帮助学生灵活地选择解题切入点，提高综合思维能力；才能帮助学生积累解题经验，丰富解题方法，学会如何综合运用已有的知识不断提高解题能力；才能让学生沟通各知识的内涵和外延，深化知识，培养发散性和创造性思维；才能让学生多解归一，学习提炼、分析问题和解决问题的通性、通法，从中择优，培养聚合思维；才能达到培养中学生举一反三的创新能力的目的，使他们不但能解同类题、相似题，甚至从未见过的题。这样在考试中就能节省时间，为考取高分提供了保障；就能培养出有综合分析能力、善于解决问题的人才。

初中学生思维能力、想像能力、分析问题能力还不是很强，思维具有狭窄性，这就需要教师在平时的教学中针对教学目的、重难点等对学生进行多方面的详细讲解和综合训练，才能取得预期的教学效果。

下面我就教学中遇到的一些典型例题分析各种解法和教法。

二、一题多解的实用题型及培养途径

（一）列方程解应用题题型

例1：将进价为40元/个的商品按50元/个出售时，就能卖出500个。已知这种商品每个涨价1元，其售量就减少10个。问为了赚得8000元的利润，售价应定为多少？商家为了用最少的成本获利仍为8000元，应怎样定价？

先帮助学生理顺各个数量关系，明确“总利润＝单件利润×数量”。

解法一：直接设题法。

设每个商品的售价为x元，则：[500-10（x-50）]（x-40）=8000。解得x1=60, x2=80。因为要获取同等利润定价高时进商品个数就少，用的成本就少，故商家为了用最少成本仍获利为8000元，售价应定为80元。

解法二：简接设题法。

设售价提高x元，则：(500-10x)（50+x-40）=8000 解得x1=10,x2=30 所以售价定为50+10=60或者50+30=80，结论同上。

（二）解直角三角形的边角关系题型

例2：河对岸有一高层建筑物AB，为测其高，在C处由点D用测量仪测得顶端A的仰角为30°，向高层建筑物前进50米，到达E处，由点F测得顶点A的仰角为45°，已知测量仪高CD=BF=1.2米，求高层建筑物AB的高。

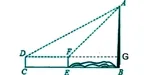
我引导学生分析，根据题意要构建直角三角形，所以延长DF与AB交于G，本题涉及到两个直角三角形Rt△ADG、 Rt△AFG ，利用DF=DG-FGF构造方程关系式，即可求出答案。

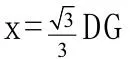
我引导学生观察，因为∠AFG＝45°，所以Rt△AFG是等腰直角三角形，得出第二种解法。

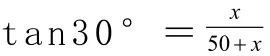
补充：假如由点F测得顶点A的仰角为60°，其它条件不变，寻找快捷的解法。经过刚才循序渐进地学习，学生们已理解透彻，一学生口齿伶俐、思路清晰地讲解了解答过程：根据题意首先构造直角三角形，延长DF与AB交于G。因为∠ADF＝60°，它是△ADF的外角，而∠ADF＝30°，所以△ADF＝30°，所以△ADF是等腰三角形，所以AF=DF=50米，然后根据AG=50sin600即可求出答案。教室里顿时响起雷鸣般的掌声。这不仅是题目的拓展，更是对知识的巩固。

让学生口述解题思路是一种值得学习和借鉴的教学方法。因为这种训练活动使学生的思维活跃起来，潜能得以充分的挖掘，课堂上气氛热烈、精采纷呈；更体现了学生的主体地位，提高了课堂实效，发展了学生思维能力，增强了合作、竞争意识，提升了解决问题的能力。

（三）应用二次函数的题型

例3：一座拱桥的轮廓是抛物线型（如图1所示），拱高6m，跨度20m，相邻两支柱间的距离均为5m。将抛物线放在所给的直角坐标系中（如图2所示），求抛物线的解析式。

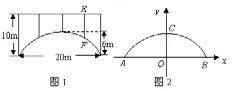
解法一：因为抛物线的顶点在y轴上，所以用特殊解法。

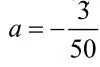
解法二：因为已知三个顶点坐标，所以设一般式。

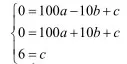
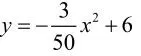
解法三：因为知道函数图像与x轴的两个交点坐标，所以设交点式。

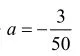
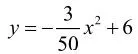
显然，第一种解法是常用解法，但我们也要认同学生的其它解法，让学生在完全理解的情况下选择自己喜欢的方法。

三、研究“一题多解”时应注意的问题

第一，对于一题多解的题，不用刻意强调最简洁方法。因为，对于一道题，因学生的个体差异，会形成不同的解题思路，让学生挑选适合自己的解法，这样才能培养学生的发散思维，如果刻意的强调某种解法，会限制学生的思维发展。

第二，不要单纯地追求一题多解，而是要着重通过练习活动，达到锻炼思维、拓宽思路、增长知识、培养和提高创造性学习能力这个根本目的。

第三，要在学生对某部分知识或某几部分知识熟练掌握、在综合练习时进行较恰当。

第四，必须以班级、学生的具体情况而定，不要挫伤学生的学习积极性。

总之，一题多解的训练，最后要多解归一，培养学生的思维聚合性。任何一个创造过程，都是发散思维和聚合思维的完美结合。而多解归一的训练，则是培养聚合性思维的重要途径。培养学生抓住问题实质的能力，达到触类旁通、举一反三、事半功倍的学习效果，是教学的最终目的。