函数最值问题在中学数学解题中的运用
广西柳州市柳石路第三小学 钟苏丽
一、前言
设函数f(x)在区间[a,b]上有定义,如果x0∈[a,b],对于任意x0∈[a,b],都有f(x0)≥f(x)[或f(x0)≤f(x)],就称是f(x0)在f(x)区间[a,b]上的最大值(或最小值)。最大值与最小值统称为最值。
在生产实践中,为了提高经济效益,必须要考虑在一定的条件下,怎样才能使用料最省,费用最低,效率最高,收益最大等问题。这类问题在数学上统统归结为求函数的最大值或最小值问题。最值问题主要讨论问题的两个方面:最值的存在性;最值的求法。
函数是中学数学的主体内容,贯穿于整个中学阶段,而函数最值问题是函数的重要组成部分。函数最值问题往往与三角函数、二次函数、一元二次方程、不等式及某些几何知识紧密联系,在解析几何还尤其表现为长度、面积的最值等。处理函数最值的过程就是实现新问题向旧问题的转化,复杂问题向简单问题的转化,实现未知向已知的转化。虽然解决问题的具体过程不尽相同,但就其解决方法来说,初等函数求最值的八种常见方法有:配方法、反函数法、判别式法、重要不等式法、线性规划法、换元法、几何法、求导法。
二、配方法在求解函数最值中的运用
对于二次函数和经换元可化为二次函数的函数求最值,常用配方法。配方法求函数的最值就是将函数解析式化成含有自变量的平方式与常数和,然后根据变量的取值范围确定函数的值域(或最值),但对一些形式上不是标准二次式的表达式,常常需要经过适当的变换,才能配方。现就一些使用配方法的题目举例如下。
例:求函数的值域。
解:由3+2 x-x2≥0,得-1≤x≤3,
因为,
所以当x=1时,ymin=2;当x=-1或3时,ymin=4,所以原函数的值域为:{y|2≤y≤4}。
三、反函数法在求解函数最值中的运用
1.二次函数运用反函数法求最值
由原函数反解出x=f(y),根据x的范围求出y的范围,进而得到y的最值的方法称为反函数法。此方法适用于能顺利求得反函数的函数,如形如y=a2+bx+c(a≠0)的函数,类似地,此方法也可推广到可以解得g(x)=f(y),且已知g(x)的取值范围的函数。
2.三角函数运用反函数法求最值

四、判别式法在求解函数最值中的运用
对于所求的最值问题,如果能将已知函数式经适当的代数变形转化为一元二次方程有无实根的问题,则常可利用判别式求得函数的最值。

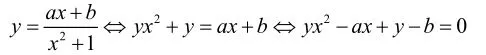
因为x∈R所以,
即4y2-4by-a2≤0,
由题意得:
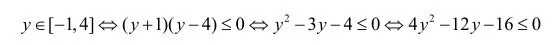
所以4b=12,a2=16,即b=3,a=±4。

五、重要不等式法在求解函数最值中的运用
1.用均值不等式求最值

运用均值不等式求最值,必须具备三个必要条件,即“一正二定三等”,缺一不可。“正”是指各项均为正数,这是前提条件;“定”是指各项的和或积为定值;“等”是等号成立的条件。
2.用柯西不等式求最值
柯西不等式:
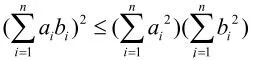
3.用琴森不等式求最值
琴森不等式:如果y=f(x)在某区间上是凹函数,则对于该区间上任意


六、线性规划法在求解函数最值中的运用
简单线性规划问题,实质是二元一次函数在定义域(即线性约束条件所表示的区域)内求最值问题,我们可用转化的思想,将二元一次函数在定义域(即线性约束条件所表示的区域)内求最值问题转化为一元函数在定义域内求最值的问题。
求线性目标函数在线性约束下的最大值和最小值问题,称线性规划问题,其解题步骤一般是:据题意建立数学模型;出所求的目标函数;将各顶点的坐标代入目标函数,即可求得最值。
七、换元法在求解函数最值中的运用
用换元法求函数最值,就是根据函数表达式的特点,把某一部分看作一个整体或用一个新变元来代替,达到化繁难为简易,化陌生为熟悉,从而使原问题得解。换元法通常有三角代换和代数代换两种。用换元法时,要特别关注中间变量的取值范围。
第一,三角代换法求最值。
对于某些函数的最值,可利用三角代换巧妙地求解。在作代换时,可根据不同的函数解析式作相应的代换。如x2+y2=a2(a>0),可令;可令。
第二,用代数代换法求最值。
八、几何法在求解函数最值中的运用
某些二元函数最值问题具有图形背景,这时我们可以将所给函数表达式化为具有一定几何意义的代数表达式,再利用几何图形,对函数最值作出直观的说明和解释。
九、求导法在求解函数最值中的运用
设函数f(x)在[a,b]上连续,在上可导,则f(x)在[a,b]上的最大值和最小值为f(x)在(a,b)内的各极值与f(a),f(b)中的最大值与最小值。要求三次及三次以上的函数的最值,以及利用其他方法很难求的函数似的最值,通常都用该方法。导数法往往就是最简便的方法,应该引起足够重视。本文以多种方法分别求解了一些不同类型的函数的最值,丰富了函数最值的求解方法。事实上求函数最值这类问题的方法除了上述这些常用方法以外,在高中数学中还有复合函数法,放缩法等,应该说函数的最值的求解方法灵活多样,通过以上的归纳能够对函数最值求法有一个系统的掌握,还要掌握各数学分支知识,能综合运用各种数学技能,然后灵活选择合理的解题方法。本文的出发点是丰富函数最值方法,以及更进一步理解函数最值的意义,所以在文中所讨论的是一些基本方法在函数最值中的应用.本文的不足点就是文中所讨论的函数最值的解法有限.本文的优点是丰富了求解函数最值的方法,更深刻地理解函数最值的意义和内容。

