无线传感网中多重绕射的UTD-PO方法研究
韩涛 邝兆轩 王红成 李秀平
(东莞理工学院 电子工程学院,广东东莞 523808)
无线传感器网 (Wireless Sensor Network,WSN)是由部署在监测区域内大量的廉价微型传感器节点组成,通过无线通信方式形成的一个多跳自组织网络。2002年美国联邦通信委员会 (FCC)批准了超宽带 (UWB)技术用于民用,从此UWB技术受到了人们的极大关注,其应用也成为近年来的研究热点[1]。由于UWB通信系统具有传输速率高、测距精度高和结构简单的特点,UWB技术已被广泛应用于无线传感器网中。在无线传感器网中,数据传输速率往往比较低 (50 kb/s~1 Mb/s),UWB信号在无线传感网络中的传输距离会超过100 m[2]。在这个传播范围内,无线传感器网能够广泛应用于军事、航空、反恐、防爆、救灾、环境、医疗、保健、家居、工业、商业等领域[3]。无线环境中信号的传播特性是所有无线通信理论研究的基础,直接关系到工程设计中通信设备的能力、天线高度确定、通信距离的计算,以及为实现优质可靠通信所必须采用的技术措施等一系列系统设计问题[4]。因此,分析无线传感网中UWB信号的传播特性对于基于的UWB无线传感器网系统的设计和测试而言,是一个必不可少的环节;和UWB系统本身一样,UWB信号传播特性的研究也是一个新兴的热点研究领域。
在城市环境下的无线传感网中,传感器会被放置于不同的环境中。在传感器发射的UWB信号的传播路径上,往往会遇到成排的建筑物。基于时域一致性绕射理论 (TD-UTD)的方法已经被广泛应用于分析UWB信号经历单个建筑物绕射后的时域传播特性。TD-UTD方法在分析UWB信号多重绕射传播特性时,需要在过渡区引入复杂的斜率绕射项[5]。因此,TD-UTD方法无法分析无线传感网中建筑物数目比较多的多重绕射模型。文献 [6]将物理光学 (PO)的方法引入到时域一致性绕射理论中,利用UTD-PO的方法分析了平面波入射条件下多重绕射的路径损耗。本文利用基于时域UTD-PO的方法来分析UWB信号经历多重劈形障碍物绕射后的时域传播特性。该方法利用一组递推关系来代替处理时域一致性绕射理论中复杂的斜率绕射项,推导了Bertoni模型[7]的时域传播系数。利用简单的卷积运算,可以分析UWB信号在无线传感网中的多重绕射传播特性。
1 UWB信号的多重劈绕射模型
本文研究的无线传感网中的UWB信号传播模型如图1所示。在这个传播模型中,N个劈形障碍物的高度为h,每个劈形障碍物的内角为γi,相邻两个劈形障碍物间的距离为w;高度为H的发射天线距离最左边的劈形障碍物的水平距离为d;接收天线的高度为h,和最右边的劈行障碍物的水平距离为d。当发射天线的高度大于障碍物高度的时候,发射天线的顶点距离各个劈形障碍物的顶点间的距离为Si,发射天线发射入射波投射到第一个障碍物时和水平方向的夹角为α。
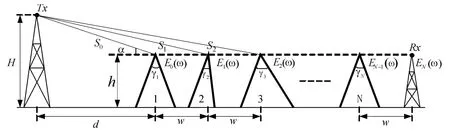
图1 无线传感网中,UWB信号多重劈形障碍物绕射传播模型
2 频域模型
文献[6]用物理光学的方法分析多重传播模型的时候,利用一组递推关系来代替一致性绕射理论中的斜率绕射项。因此,利用基于UTD-PO的方法来分析上述含有多个劈形障碍物的多重绕射模型时,只需要计算一条射线的绕射问题,而接收点的场可以利用一组递推函数来表示。考虑到发射天线的高度在大于或小于障碍物高度时候,UWB信号在图1所示的传播环境中有着不同的传播机制,根据文献[6]中的分析方法,下面分别推导发射天线的高度在不同范围内,图1所示传播模型中接收点的场强在频域内的表达式。
2.1 发射天线的高度大于或等于障碍物的高度 (H≥h)
在发射天线的高度大于或者等于障碍物的高度时候,接收点接收到的信号不仅包括经发射天线发射的直达信号也包括经过障碍物多重绕射后的UWB信号。利用UTD-PO的方法在频域内接收点的场强可以表示为一组简单绕射后的算术平均值,接收点的场强在频域内可以表示为:

其中Em(ω)是第m+1个障碍物处的电场强度。距离参数可表示为:
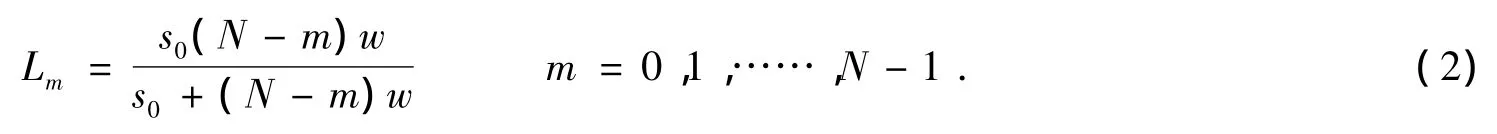
根据球面波的传播特性,入射到第一个障碍处的UWB信号的电场强度可表示为:

其中是发射天线发射的球面UWB信号的幅度,k是波数。D(ω,Lm)是UWB信号经历劈形障碍物的频域绕射系数[8],可以表示为:
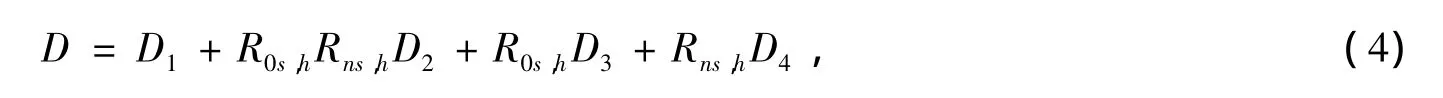
其中Di的表达式为:
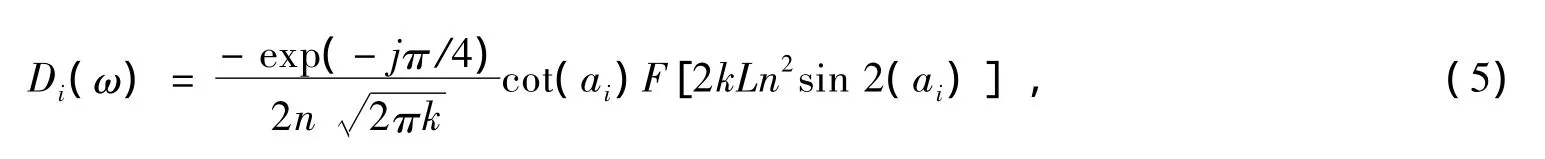
其中

式中的φ个φ'可由下式确定:

nπ是劈形障碍物的内角。
2.2 发射天线的高度小于障碍物的高度 (H<h)
在发射天线的高度小于障碍物的高度时候,接收点接收到的信号仅包括经过障碍物多重绕射后的UWB信号。利用UTD-PO的方法在频域内接收点的场强可以表示为:

3 时域模型
得到上述频域递推关系后,接下来利用拉普拉斯变换可以推导相应的时域递推关系,利用时域递推关系可以预测上述模型中UWB信号的多重绕射传播特性。
3.1 发射天线的高度大于或等于障碍物的高度 (H≥h)
对式 (1)两边同时进行拉普拉斯变换可以得到如下时域递推关系:

其中e0(t)是经发射天线发射的UWB信号入射到第一个障碍物处的时域信号,可以表示为:

p(t)是发射天线发射的UWB信号,em(t)表示在第m+1个障碍物处的时域信号,c是光速,“*”符号表示卷积运算,δ(t)是Dirac Delta函数。“s”和“h”分别代表水平极化和垂直极化。ds,h(t,Lm)是劈形障碍物的时域绕射系数,根据式 (4)的频域表达式,利用拉普拉斯变换其时域表达式可以表示为:
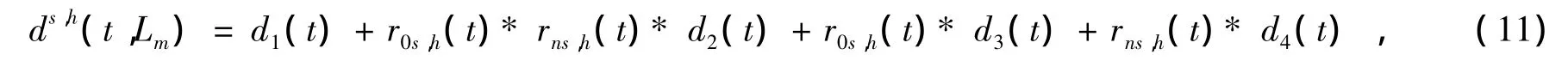
文献 [9]给出了r0s,h(t)为时域Freshnel反射系数,di(t)在文献 [5]已经定义给出,在这里重新将其改写为简单的形式:
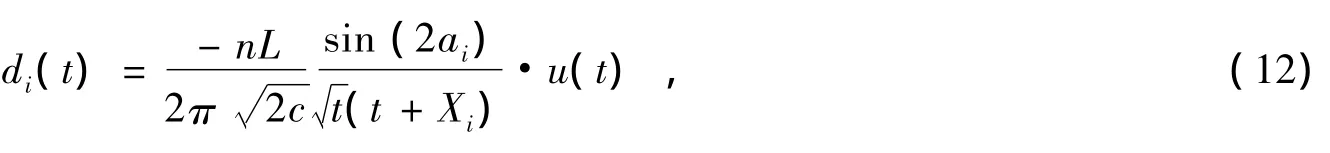
其中Xi=2Ln2sin2(ai)/c,ai由式 (6)定义给出,u(t)是阶跃函数。
3.2 发射天线的高度小于障碍物的高度 (H<h)
对式 (8)两边同时进行拉普拉斯变换可以得到如下时域递推关系:

4 仿真结果
本节利用文中提出的时域方法来预测图1这种典型传播环境下接收点的UWB脉冲信号。假设图1所示的传播环境中,发射天线距离右边第一个障碍物的水平距离d=8 m;发射天线和接收天线之间劈形障碍物的高度h=4 m,相邻两个劈形障碍物之间的水平距离w=4 m;接收天线的高度和劈形障碍物的高度相同,距离左边最近的障碍物的水平距离也为w=4 m;建筑物的相对介电常数εr=5.5,电导率为σ=0.023 S/m。使用的UWB信号是高斯二阶导脉冲信号,这种信号的数学表达式为:
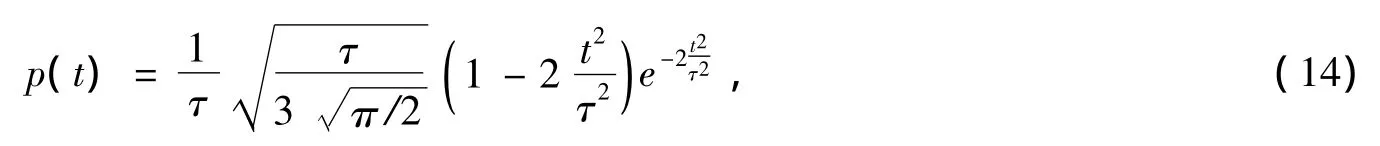
其中τ决定信号的脉冲宽度,这里τ=0.1 ns。在仿真中,天线的高度参数H和障碍物的个数参数N可以根据仿真的需要调整。

图2 H=5 m时含有2个劈形障碍物的传播环境下接收点的波形
为了验证本文方法的正确性,首先假设图1所示的传播环境中有两个内角为γ1=γ2=π/3的劈形障碍物,分别用本文提出的时域方法和文献[5]中基于斜率绕射场的方法预测含有两个劈形障碍物的传播环境中接收点的波形。假设天线发出两个水平极化脉冲,发射天线高度H=5 m(H≥h)时,接收天线处的UWB信号如图2所示;在发射天线高度H=3 m(H<h)时,接收天线处的UWB信号如图3所示。从图2和图3中可以看出,利用本文提出的时域方法预测的接收信号和利用文献 [5]中的方法预测的信号吻合的很好。因此,本文提出的时域方法能够有效地应用于分析多重劈形障碍物绕射模型。另外,图2和图3中接收天线处的UWB信号形状有明显差别,这是因为在发射天线的高度大于或者等于障碍物的高度时候,接收点接收到的信号是经发射天线发射的UWB信号和经过障碍物多重绕射后的UWB信号的叠加型号,在发射天线的高度小于障碍物的高度时候,接收点接收到的信号仅包括经过障碍物多重绕射后的UWB信号。

图3 H=3 m时含有2个劈形障碍物的传播环境下接收点的波形
为了研究不同内角的劈形障碍物对接收天线处接收到UWB信号的影响,我们分别用不同内角的劈形障碍物来预测UWB信号的多重绕射传播特性。假设图1所示的传播环境中含有两个内角分别为γ1和γ2的劈形障碍物,高度H=3 m发射天线分别发射三个水平极化UWB脉冲信号,我们分别预测在①γ1=π/3,γ2=2π/3;②γ1=π/3,γ2=π/3;③γ1=π/3,γ2=π/6三种不同内角劈形障碍物组合下,接收天线处的波形,如图4所示。从图4中我们可以清楚地发现,劈形障碍物的内角对接收天线处的波形有明显影响。劈形障碍物的内角越小,接收天线处的波形失真和幅度衰减越大。
为了说明本文中所提出的UTD-PO方法相比文献[5]中的方法在研究大量障碍物环境下多重绕射的时域特性更具有优势,我们用本节所提出的UTD-PO方法来预测UWB信号经过多个劈形障碍物绕射后的UWB信号。假设在劈形障碍物的个数分别为4和6时,高度为m发射天线分别发射一个水平极化UWB信号,利用上述UTD-PO的方法预测接收点的UWB信号,如图5所示。从图5中可以发现,随着劈形障碍物数目的增加,接收点的信号波形失真更为明显。另外,为了说明本文中基于UTD-PO的方法相比基于斜率绕射场的UTD方法具有更高的运算效率,我们分析了障碍物数目为2、4和6时,利用文献[5]中基于斜率绕射场的方法和基于时域UTD-PO的两种方法预测接收点波形的运算时间比TTDUTD/TTDUTD-PO,如表1所示。从表1中可以看出随着障碍物数目的增加,本文提出的时域方法在运算时间上的优势更为明显。这是因为对于含有n个劈形障碍物的传播环境中,利用基于斜率绕射场的一致性绕射理论需要处理2n条绕射射线;利用本文提出的方法,在计算过程只需要考虑1条经第一个障碍物绕射后的绕射射线,接收点的多重绕射信号可以看成一组绕射信号的算术平均值。因此,本文中所提出的时域方法不仅能够有效地应用于分析含有多个劈形障碍物的多重绕射模型,而且还能够明显节省计算时间。
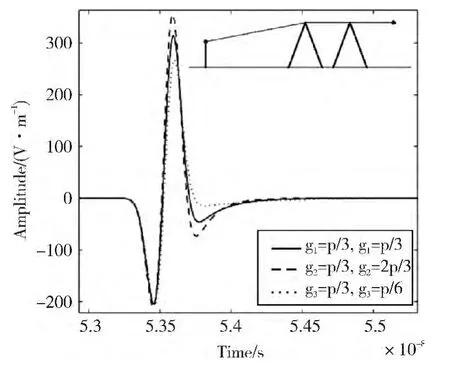
图4 m时含有2个不同内角的劈形障碍物的传播环境下接收点的波形

图5 H=3 m时含有4个和6个劈形障碍物的传播环境下接收点的波形比较
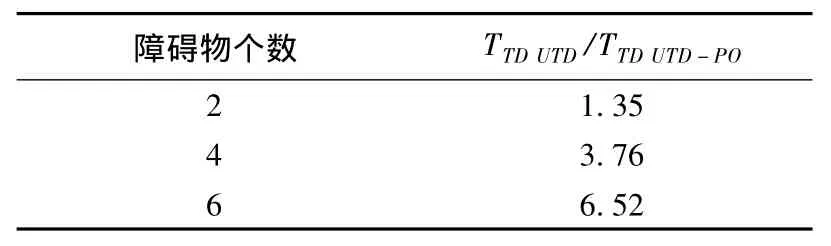
表1 不同障碍物个数下两种预测方法运算时间比
5 结语
本文利用物理光学方法在分析多重绕射时的优势,在时域内引入物理光学理论改进了时域一致性绕射理论,并利用这种基于时域的UTD-PO的方法分析了多重劈形绕射传播模型。结果表明这种方法不仅能够准确有效地应用于分析多重劈形绕射传播模型,而且随着绕射障碍物数目的增加这种方法的运算效率更高。另外,根据无线传感网中障碍物的几何尺寸,选择不同内角的劈形障碍物来等效无线传感网中的障碍物,可以得到更加准确地预测结果。
[1]Oner M.On the Spectral Correlation of UWB Impulse Radio Signals[J].IEEE Commun Lett,2008,12(10):714 -716.
[2]Gezici S,Tian Z,Giannakis G B,et al.Location via ultra-wideband radios[J].IEEE Signal Process Mag,2005,22(4):70–84.
[3]Zhou C,Qiu R.Pulse distortion caused by cylinder diffraction and its impact on UWB communications[J].IEEE Transactions on Vehicular Technology,2007,56(4):2385 -2391.
[4]Qiu R C.Generalized time domain multipath channel and its application in ultra-wideband(UWB)wireless optimal receiver design—Part III:System performance analysis[J].IEEE Trans Wireless Commun,2006,5(10):2685 -2695.
[5]Karousos A,Tzaras C.Multiple time-domain diffraction for UWB signals[J].IEEE Transactions on Antennas and Propagation,2008,56(5):1420-1427.
[6]Han T,Long Y.Time-domain UTD-PO analysis of a UWB pulse distortion by multiple-building diffraction[J].IEEE Antennas and Wireless Propagation Letters,2010(9):795 -798.
[7]Bertoni H.Radio Propagation for Modern Wireless Systems[J].Englewood Cliffs,NJ:Prentice-Hall,2000:187 -198.
[8]Holm P D.A new heurisitic UTD diffraction coefficient for nonperfectly conducting wedges[J].IEEE Trans IEEE Transactions on Antennas and Propagation,2000,48(8):1211-1219.
[9]Rousseau P,Pathak P.Time-Domain Uniform Geometrical Theory of Diffraction for a Curved Wedge[J].IEEE Transactions on Antennas and Propagation,1995,43(12):1375-1382.

