基于云模型和粗糙集的特征选择算法

黄巧云

(福州大学至诚学院 计算机工程系，福建福州 350002)

入侵检测系统是通过收集和分析系统日志，从而对网络状态做出正确的判断［1］。但由于其日志中含有大量的冗余数据，因此如何快速、有效地从数据中获取安全威胁信息，成为当前的研究热点。目前，人们主要通过特征选择来消除冗余数据，在保证分类精度的前提下，通过降低特征空间的维度，从而快速、有效地提取网络安全信息［1］。

粗糙集理论中的属性约简在特征选择上具有天然的优势，它能够在保持信息系统的分类精度的条件下，删除冗余的属性［2］。然而，基于粗糙集的属性约简大多是基于启发式信息的算法，而这些算法的计算结果都是唯一的。但对于同一张数据表，不同属性数据的提取难易程度不一样，而且不同的人所关注的属性也可能不同。因此若属性约简的结果是较难提取的数据属性，或者是人们所不关注的，那么属性约简的意义就大打折扣。文献［3］提出了一种基于属性序的约简算法，它能根据不同的属性序，得到不同的约简结果。然而，基于属性序的约简方法一般都是根据专家的意见或是操作者的经验给出，主观性比较大，不能很好地根据数据的实际分布情况给出属性序［4］。

因此，本文在此提出一种基于云模型和粗糙集的特征选择算法Cloud_Rough，通过云模型对入侵检测系统日志属性进行排序，解决了由专家给定属性序的主观偏好的问题，在此基础上，利用粗糙集进行基于属性序的约简。在实际应用中，利用基于云模型的属性序算法得到的权重排序后，还可以根据专家的意见对属性序进行适当的调整，从而保证了属性序的给定既符合数据的实际分布，又能满足对属性偏好的需求。

1 理论研究

1.1 云模型

设论域U={x1，x2，…，xm}，A是关于U上的定性概念，若论域中的元素xi对A的隶属确定度CA(xi)∈［0，1］是一个有稳定倾向随机数，则确定度CA(xi)在论域上的分布称为云模型，简称云［5］。

云的数字特征可以用期望值Ex，熵En和超熵He三个数值来表示，其中，期望值Ex反映模糊概念的信息中心;熵En指云的期望曲线的带宽，是概念模糊度的度量;超熵He反映云的离散程度［5］。如式 (1)所示:

定义1 U是n维空间的论域，U={x1，x2，…，xm}，xi表示U中的第i类对象，xij则表示xi在第j维属性空间的取值［6］，根据云模型的定义，可对其建模如下:

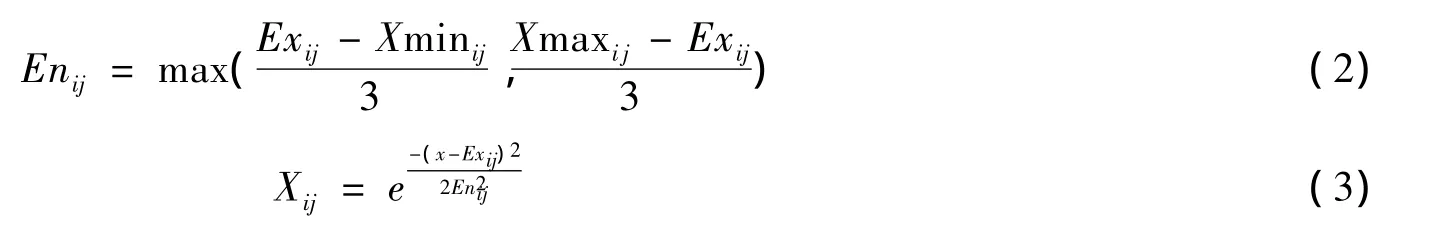
其中，Exij表示xij的重心点，即该云模型范围内的高频率元素;Enij来描述云模型覆盖的数值范围;Xminij表示该维属性空间的最小值点;Xmaxij表示该维属性空间的最大值点;Xij表示在云模型的范围内任意一属性值所对应的隶属度。

定义2 U是n维空间的论域，两个对象xi，xj∈U，d(xik，xjk)表示两个对象在第k维属性空间的距离［7］。

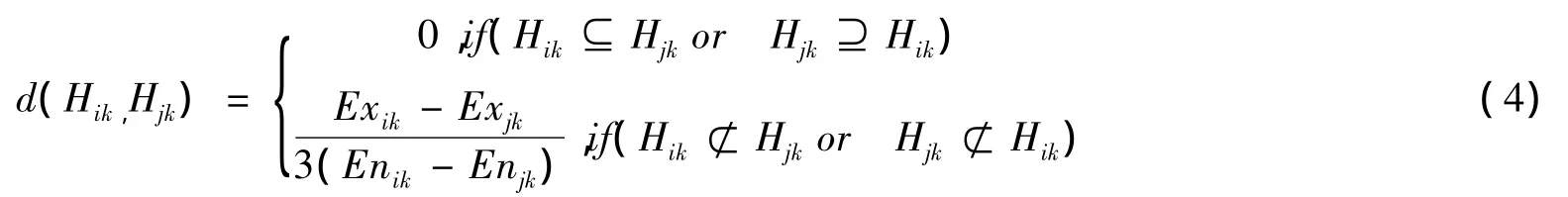
根据云的3En规则［8］，当d(Hik，Hjk)≥1时，说明两个对象空间是相离的，第k维属性可区分度高;当d(Hik，Hjk)=0时，说明两个对象空间完全重全，第k维属性可区分度低。

定义3 U是n维空间的论域，U={x1，x2，…，xm}，根据定义2，第k维属性的类别间距离可以定义如下:

定义4 U是n维空间的论域，任意两个对象xi，xj∈U，当d(xik，xjk)越大，则第k维属性的可区分度越大，该属性在分类的作用中越大，因此第k维属性权重可以定义如下:

1.2 属性约简

属性约简［2］作为粗糙集理论的一个重要组成部分，能够在保持信息系统的分类精度的前提下，删除冗余的属性，快速获取有效数据。

定义5 设决策属性集D，条件属性集U/ind(D)={Y1，Y2，…，Yt}的正区域［2］可计算如下:

定义6 设M是决策表S的可辨识矩阵，∀mij∈M，mij中的属性从左到右继承着序列SO，在序SO下mij中的第一个属性称为标签属性［9］。

定义7 令M是决策表S=＜U，C∪D，V，f＞的可辨识矩阵。R(R⊆C且R≠Φ)是一个约简，当且仅当∀α∈M(α≠Φ→α∩R≠Φ)［9］。

定义8 指定标签属性ck∈C，{b}是C的一个属性子集，集合L(SO)计算如下［9］:

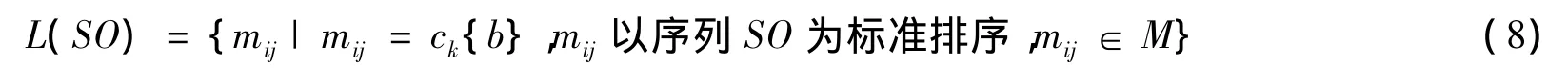
定义9 可辨识矩阵M关于L(SO)的划分［9］:

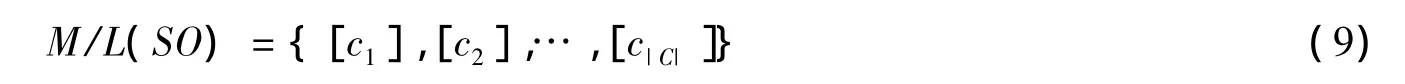
其中［ck］={mij|mij=ck{b}，mij以序列SO为标准排序，mij∈M}。

定义10 假设可辨识矩阵M的一个等价类{［c1］，［c2］，…，［c|C|］}，则最大标签属性的定义［10］:

综合上述定义，基于属性序的约简算法是在给定属性序的基础上，按照属性的重要性，将属性逐个加入集合，直到计算出一个满足的子集，再删去当中不必要的属性［9］。然而，该算法是通过遍历可辨识矩阵M来寻找非空标签属性的，这样不可避免地会带来时间和空间上较大的开销［9］。而文献 ［3］则通过引入分治法的思想，提出了一种快速计算标签属性的算法，大大降低了算法的时间和空间复杂性。

2 Cloud-Rough算法研究

本文提出的Cloud_Rough特征选择算法，通过云模型对日志属性进行排序，解决了由专家给定属性序的主观偏好的问题，然后再利用粗糙集进行基于属性序的特征选择，删除冗余的属性，以实现在海量的数据中快速提取有效的信息。

输入:决策表S=(U，R，V，f)，U为论域，R=C∪D为属性集合。

输出:特征选择子集T。

Step1:∀cj∈C，∀Xi∈U/ind(D)，根据定义1建模，分别求出云模型的期望值Exij和熵Enij;

Step2:按照第j维属性，对每类对象Xi∈U/ind(D)的重心点Exij进行升序排列，得到Ex1j≺Ex2j≺…≺Exmj，其中1≤j≤|C|;

Step3:对每一维属性，根据式 (4)计算排序后的两两对象间的距离;

Step4:根据式 (5)分别计算每维属性的类别间距;

Step5:根据式 (6)分别计算每维属性的权重，并按升序排列，从而得到属性序SO;

Step6:设C={c1，c2，…c|c|}，按照属性序SO:c1＜c2＜… ＜c|c|，r=1，T=φ;

Step7:根据式 (7)，计算正区域POSC(D);

Step8:根据文献 ［3］所提的算法，计算决策表的非空标签属性集合F;

Step9:设CN是F中标号最大的标签属性，如果CN∈T，转到Step14;

Step10:令T=T∪{CN}且CN放在T的最后一位;同时令F=F－{CN};

Step11:令C`=φ，ti为T的标签属性，按照i从大到小排列，并依次加入C'中;

Step12:令fi为F的标签属性，按照i从小到大排列，再依次加入到C'中;

Step13:令C=φ，C=C`。根据新属性序，计算非空标签属性集合F，转至Step9;

Step14:输出特征选择子集T。

3 仿真实验

3.1 实验数据

本文的实验数据采用标准数据集UCI的Heart数据源和Segmentation数据源，以及从KDD Cup 1999 Data的入侵检测系统数据库中随机抽取的10 000条记录作为测试数据。

3.2 实验分析

为了验证提出的特征选择算法的有效性，本文主要进行以下三组实验。

1)利用标准数据集UCI的Heart数据源和Segmentation数据源，属性名用Ai表示(i=0，1，2，…，n－1)，其中n为属性个数，进行云模型 (Cloud model)的属性重要性排序测试，并根据排序结果的前50%的属性，与Weka［10］数据挖掘工具里提供的Genetic Search特征选择算法选出的特征子集，以及全部属性集，利用J-48分类器进行分类，来验证该重要性排序的有效性。

表1是利用Weka数据挖掘工具所提供的J-48分类器分别对三类属性集合进行分类的结果。从表中可以看出，由云模型所选择的属性子集，分类效果与另两种方式相差不多，说明该算法选择出的50%属性的重要性。实验证明基于云模型的属性重要性排序的有效性。

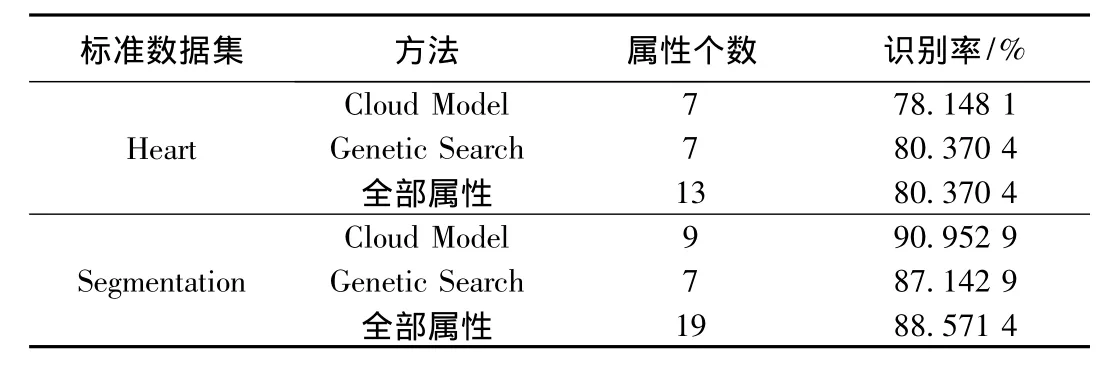
表1 不同属性子集的分类结果

2)利用Cloud_Rough算法与Weka数据挖掘工具提供的Generic Search、贪心式前向搜索和贪心式反向搜索三种算法［10］对KDD的测试数据集进行特征选择，再利用J-48分类器对约简后的特征子集进行分类，最后对测试结果进行比较。

表2为不同特征选择算法得到的属性子集，而这当中比如:服务类型 (service)、连接服务的次数(service_count)、登录状态 (logged_in)等对于分类具有较为重要意义的特征属性都包含在内。

表3是在表2的基础上，使用分类器对不同的特征子集进行分类的结果。从表中可以看出，与其它的特征选择方法相比，基于Cloud_Rough的算法，虽然约简出的特征数较多，但是分类器构建时间却不长，而且识别率最高。

表2 不同特征选择算法的特征子集

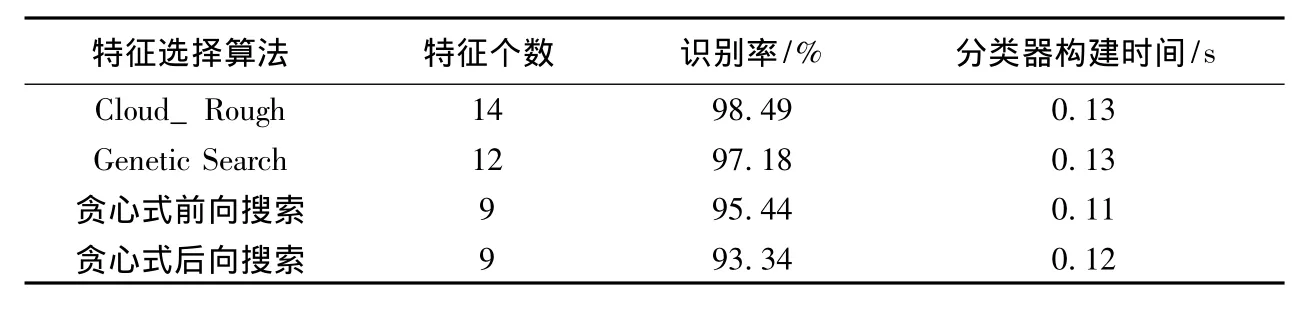
表3 不同特征子集的分类结果

3)利用Weka数据挖掘工具提供的J_48分类器与BayesNet分类器，分别对未进行特征选择的属性集和经由Cloud_Rough算法选择的属性子集进行分类。

从表4中可以看出，经过Cloud_Rough算法特征选择后，在不同的分类器下分类正确率都有所提高，而且分类器的构建时间减少。实验结果表明，本文提出的Cloud_Rough特征选择算法不仅可以适用不同的分类器，而且可以改善分类器的性能，具有较高的效率。

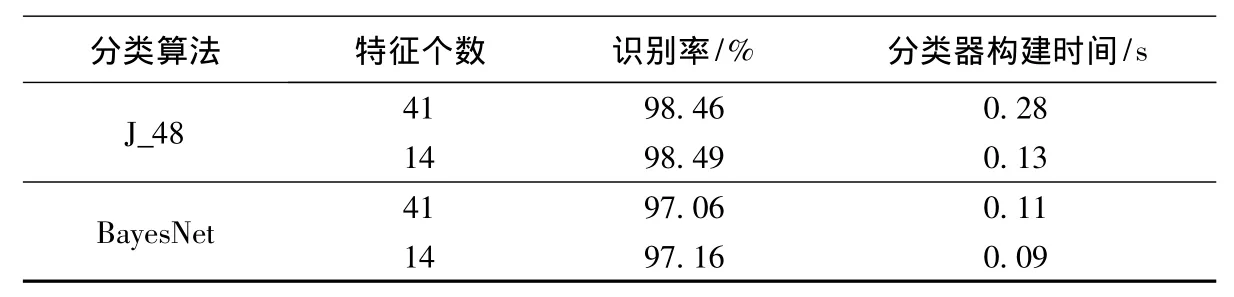
表4 不同分类器的分类结果

4 结语

本文将云模型与粗糙集相结合，通过云模型对入侵检测系统日志属性进行重要性排序，解决了由专家给定属性序的主观偏好的问题，在此基础上进行基于属性序的快速约简。实验的结果证明，该算法在大数据量下，仍能快速得到特征选择的结果，并且达到较高水平的分类效果。

［1］陈友，程学旗，李洋，等．基于特征选择的轻量级入侵检测系统［J］．软件学报，2007，18(7):1639－1651．

［2］陈昊，杨俊安，庄镇泉．变精度粗糙集的属性核和最小属性约简算法［J］．计算机学报，2012，35(5):1011－1017．

［3］胡峰，王国胤．属性序下的快速约简算法［J］．计算机学报，2007，30(8):1429－1434．

［4］关素洁．基于Rough集的属性与属性值约简方法研究［D］．江西:南昌大学，2011．

［5］李德毅．知识表示中的不确定性［J］．中国工程科学，2000，2(10):73－79．

［6］刘延华，周柳鸿，陈国龙．基于云模型的入侵检测日志数据特征选择算法［J］．福州大学学报:自然科学版，2011，39(6):812－818．

［7］张国英，沙云，刘旭红，等．高维云模型及其在多属性评价中的应用［J］．北京理工大学学报，2004，24(12):1065－1069．

［8］刘常昱，李德毅，潘莉莉．基于云模型的不确定性知识表示［J］．计算机工程与应用，2004，40(2):32－35．

［9］HU Xiao-hua，Cercone Nick．Learning in Relational Databases:A Rough Set Approach［J］．Computational Intelligence，1995，11(2):323 －338．

［10］Witten Lan H，Frank Eibe，Hall Mark A．Data Mining:Practical Machine Learning Tools and Techniques［M］．San Francisco:Morgan Kaufmann Publishers，2011．