线性流形上埃尔米特自反矩阵反问题的最小二乘解及其最佳逼近

王学锋 王江涛

(1．东莞理工学院 计算机学院，广东东莞 523808;2．华南理工大学 数学系，广州 510641)

在震动理论、电学、光学和自动控制等领域提出了最小二乘问题，而线性系统的检测和复原过程中，由于资料的不完整性或者要求对已有的资料进行校正时，又提出了矩阵的最佳逼近问题。关于最小二乘问题和最佳逼近问题的研究已取得了一系列重要成果，见文献 ［1－11］。例如，孙继广在文献［1］中利用矩阵分析的方法研究了实对称矩阵的最小二乘问题，并给出了其解的一般表达式;戴华在文献 ［2］中研究了线性流形上实对称矩阵的最佳逼近问题;廖安平等在文献 ［3］中对线性流形上实对称半正定矩阵的一类逆特征值问题进行了研究;周富照等在文献 ［4］中则研究了线性流形上对称正交对称矩阵逆特征值问题，并给出了最佳逼近解。将讨论线性流形上埃尔米特自反矩阵的最小二乘问题与最佳逼近。

首先，引入一些符号和概念。令Cm×n表示m×n型复矩阵集合，Rm×n表示m×n型实矩阵集合，Ⅰk表示k阶单位矩阵，HCn×n表示n阶埃尔米特矩阵集合，UCn×n表示n阶酉矩阵集合。A，B∈Cm×n分别表示A的Moore-Penrose广义逆与共轭转置，rank(A ) ，tr(A ) 分别表示A的秩与。对于矩阵A，B∈Cm×n，A*B表示A与B的Hadamard积，[A，B]表示A与B的内积，其定义为[A，B]=tr( BHA ) ，由此内积诱导的范数为

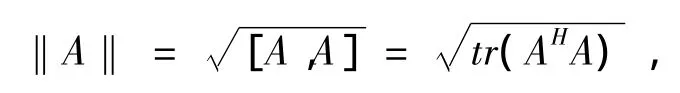
显然，上述范数是Frobenius范数，且Cm×n构成一个完备的内积空间。GRCn×n表示n阶广义反射矩阵组成的集合，即

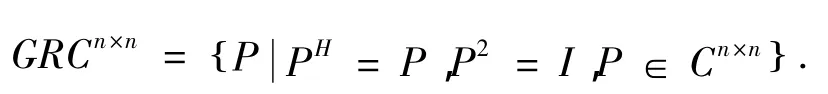
定义 给定P∈GRCn×n，称A∈Cn×n为关于P的埃尔米特自反矩阵，如果它满足:

AH=A， PAP=A．

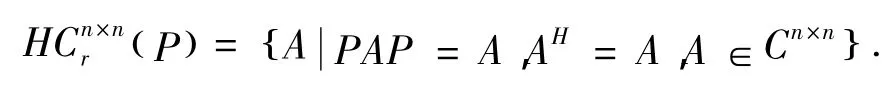
令

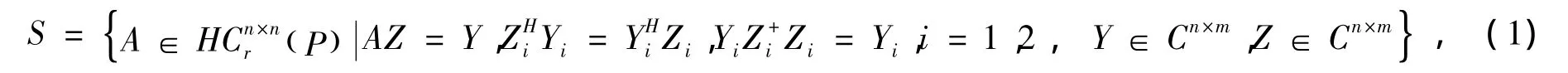
其中

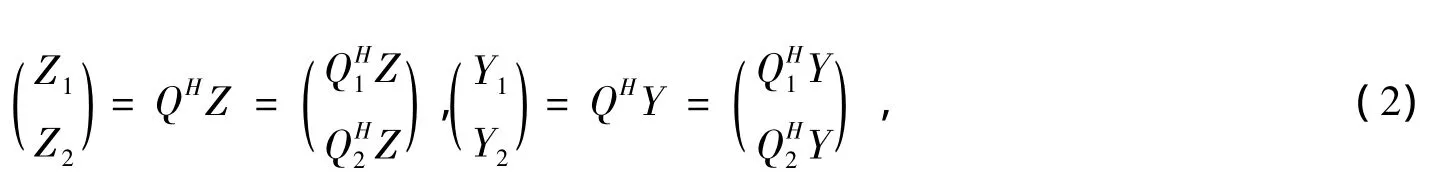
本文所考虑问题的数学描述如下:

问题Ⅰ 给定X，B∈Cn×m，求A∈S使得

问题Ⅱ 对任意给定的A*∈Cn×n，求 A^∈SX，B使得

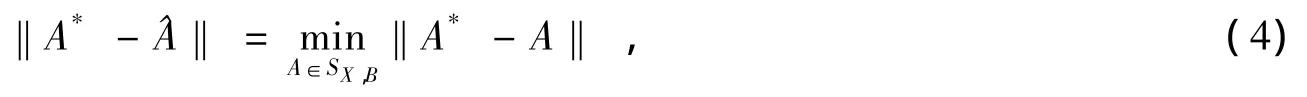
其中SX，B是问题Ⅰ的解集合。

本文结构如下:在第二节，推导线性流形S的一般表达式;第三节，建立线性矩阵方程在线性流形上可解的充分必要条件，并推导问题Ι解的一般表达式;在第四节，证明问题Ⅱ解的存在惟一性，并推导这个惟一解的表达式。

1 线性流形S的一般表示形式

由矩阵P1和P2的性质以及埃尔米特自反矩阵的定义，不难证明下面两个引理。

引理2 令

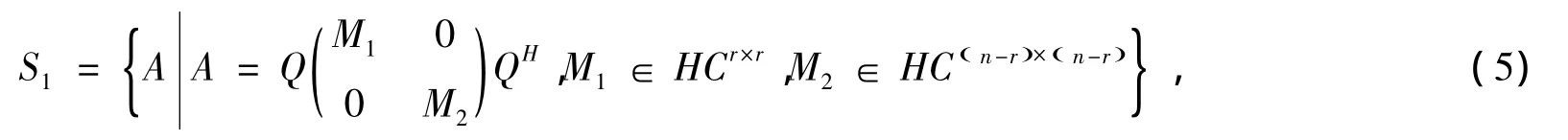
于是有S1=( P ) 。

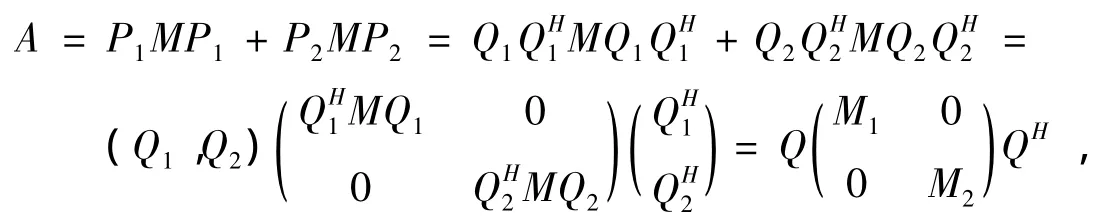
反之，对任意的A∈S，则存在矩阵M1∈HCr×r和矩阵M2∈HC(n-r)×(n-r)使得

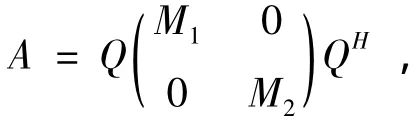
直接计算得

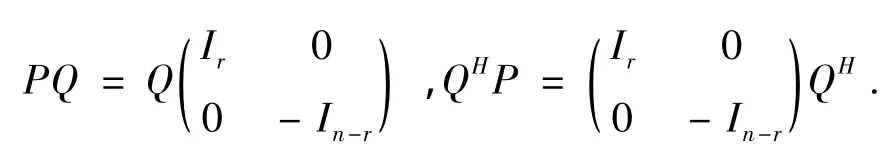
因此，

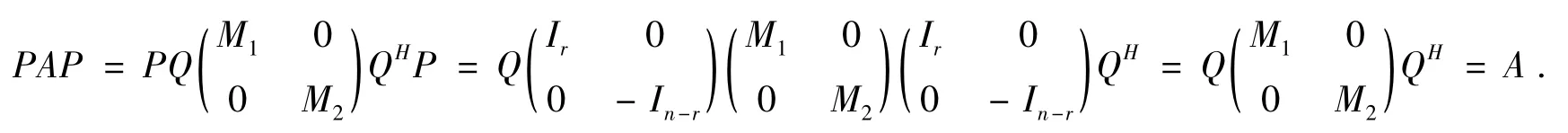
显然有AH=A。因此，A∈(P)。证毕。

引理3［1］对给定的矩阵X，B∈Cn×m，且X有奇异值分解如下

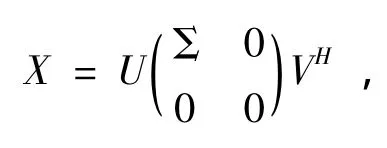
其中 U= ［U1U2］∈ UCn×n，V= ［V1V2］∈ UCm×m，k=rank(X ) ，Σ =diag(σ1，σ2，…，σk)，

σi＞ 0，i=1，2，…，k，且 Φ =(φij)∈ Ck×k，

则有下面结论:

1)矩阵方程AX=B在集合HCn×n中有解的充要条件是

BX+X=B，XHB=BHX ．

而且，当上式子成立时，其一般解可表示为

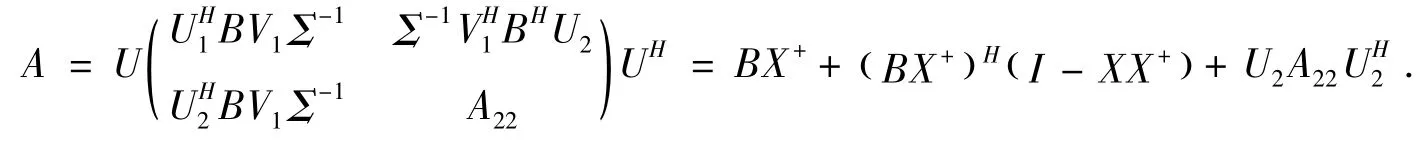
其中A22∈HC( n-k)×( n-k)为任意的。

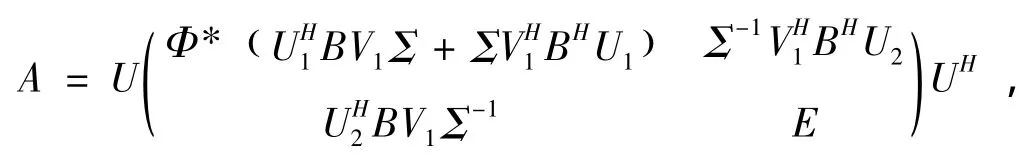
其中E∈HC( n-k)×( n-k)为任意的。

引理4 令

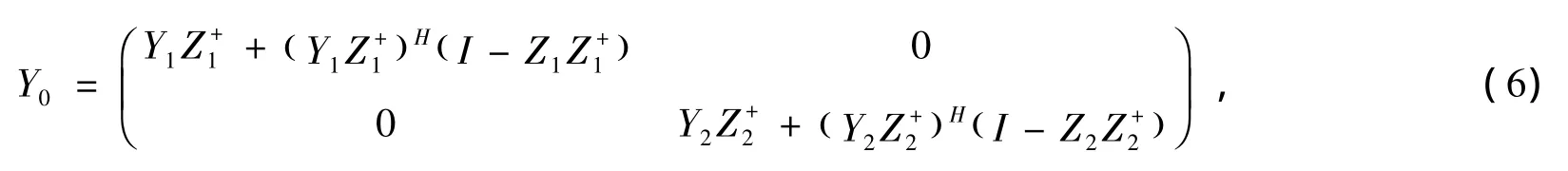
且假设矩阵Z1和Z2的奇异值分解分别是

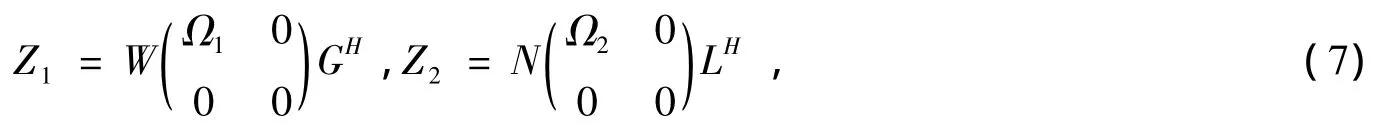
其中 W=(W1W2)∈UCr×r，G=(G1G2)∈UCm×m，N=(N1N2)∈UC(n-r)×(n-r)，L= ( L1L2)∈UCm×m，Ω1=diag ( α1，α2，…，αk1)，Ω2=diag ( β1，β2，…，βk2)，k1=rank( Z1)，k2=rank( Z2)，Zi，Yi，i=1，2 i=1，2由 (2)式定义。于是由 (1)式定义的集合S可表示为

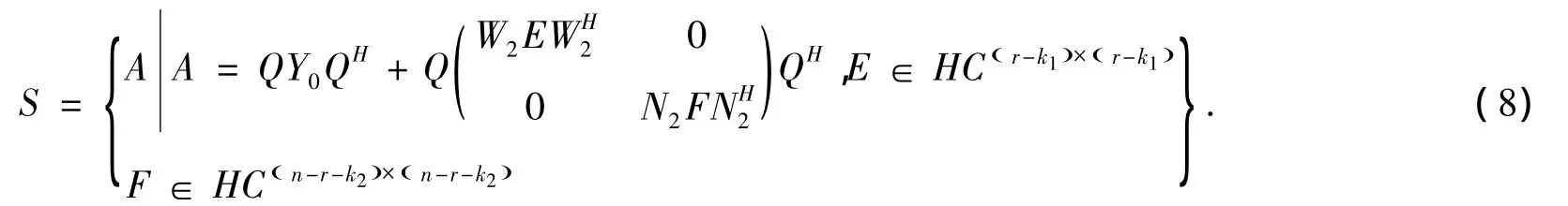
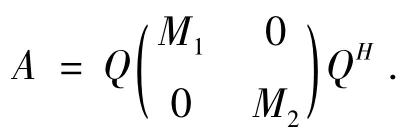
于是方程AZ=Y等价于下列方程

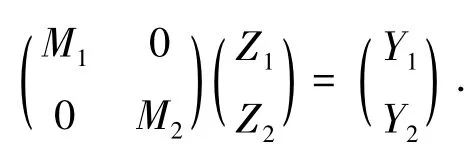
分别在 HCr×r和 HC( n-r)×( n-r)中有解。

由引理3可知，矩阵方程M1Z1=Y1在HCr×r中和方程M2Z2=Y2在HC(n-r)×(n-r)中有解的充分必要条件是

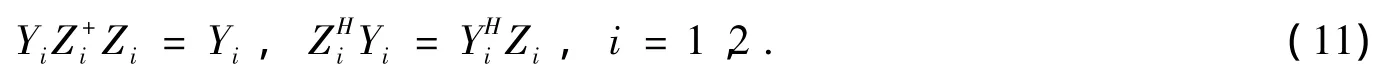
而且，当条件 (10)式成立时，矩阵方程 (8)和 (9)的解可分别表示为

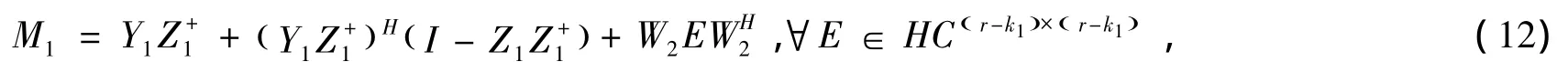
和

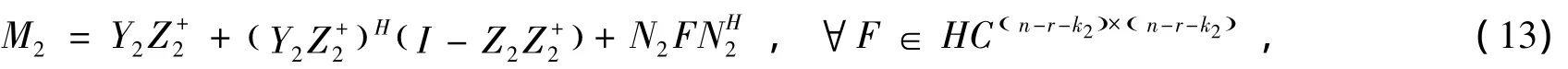
将 (12)、(13)式代入 (5)式中可得到 (8)式。证毕。

不难证明，S是一个非空的线性流形。

2 问题I的解的一般表达式

由上面给出的线性流形S的一般表达式，关于问题Ⅰ有如下结论。

定理1 给定X，B∈Cn×m，令

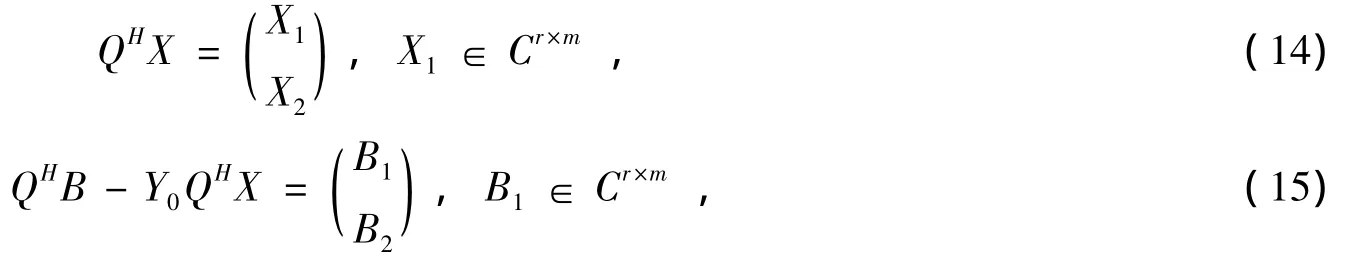
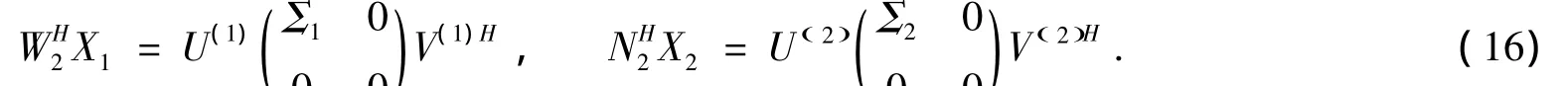
于是问题I的解可表示为

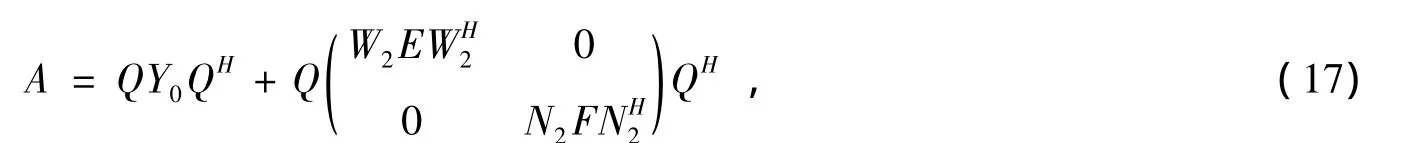
证 对任意的矩阵A∈S，由引理4和 (14)，(15)式以及F范数的正交不变性可得到，

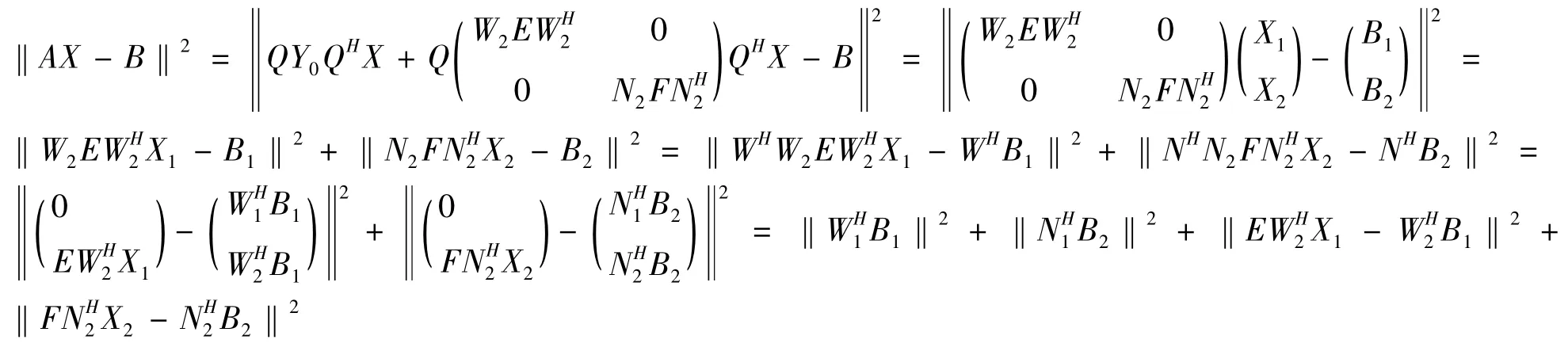
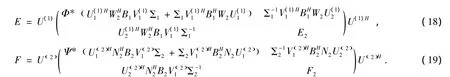
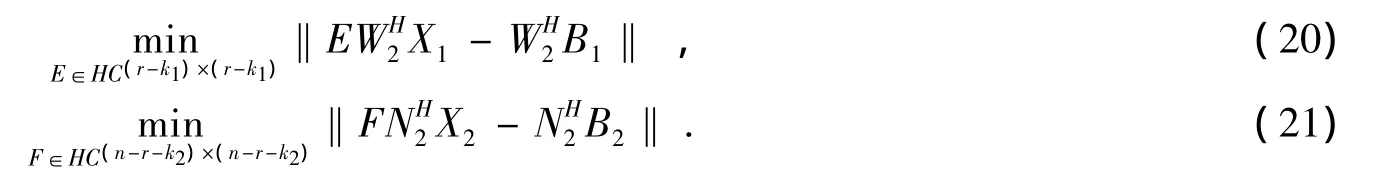
由引理3中2)可知，问题 (20)、(21)的解可分别表示为 (18)、(19)式，分别将 (18)，(19)式代入到 (8)式，即可得到问题Ⅰ的解 (17)式。证毕。

由引理3和引理4，容易证明下面的定理。

定理2 设X，B∈Cn×m，并假设条件以及符号与定理1相同，于是方程AX=B在S中可解的充分必要条件是

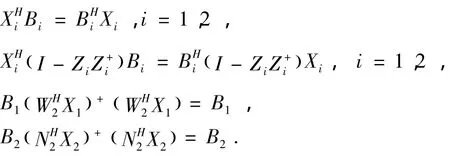
而且，在上述条件成立时，其解可表示为公式 (17)，其中

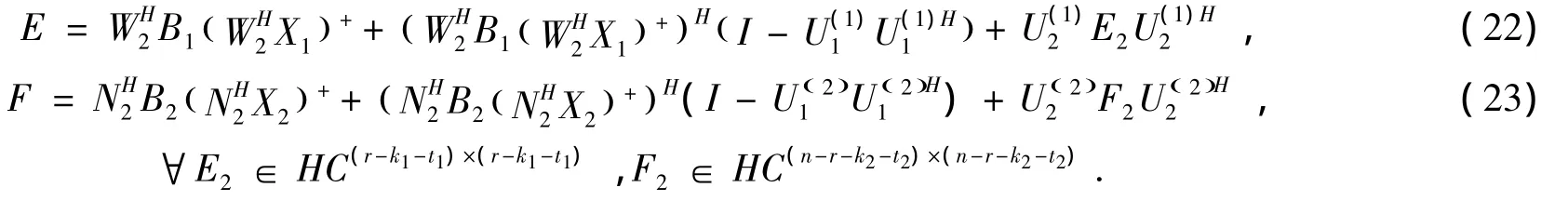
定理3 给定 X∈Cn×m，Λ =diag (λ1，λ2，…，λm) ，Γ =diag (μ1，μ2，…，μm)且在定理1中令B=XΛ，在S中令Y=ZΓ，其它条件和符号与定理1同，则方程AX=XΛ在S中有解的充要条件是

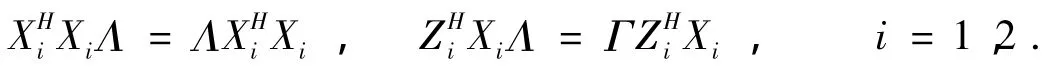
由定理2，进一步可得到线性流行S上的埃尔米特自反矩阵的逆特征值问题。

此时，问题的解可表示为公式 (17)，其中E与F可分别表示为公式 (22)与 (23)。

3 问题Ⅱ解的一般表达式

在本节中，将证明问题Ⅱ解的存在性与惟一性，并推导其惟一解的表达式。

引理5［12］设 C，D ∈ Cn×n，若 D=DH，则有

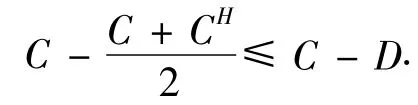
定理4 假设条件和符号与定理1同，对于任意给定的A*∈Cn×n，且记

于是问题Ⅱ有惟一解，且这个解可表示为

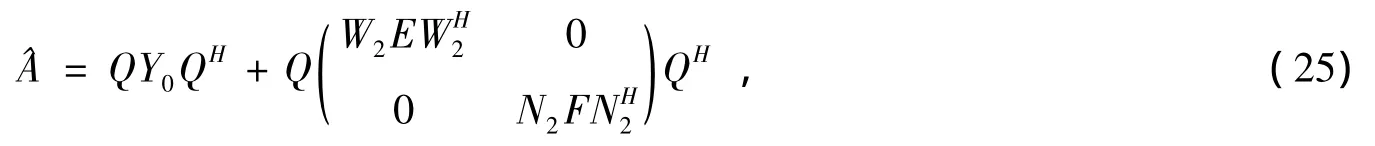
其中

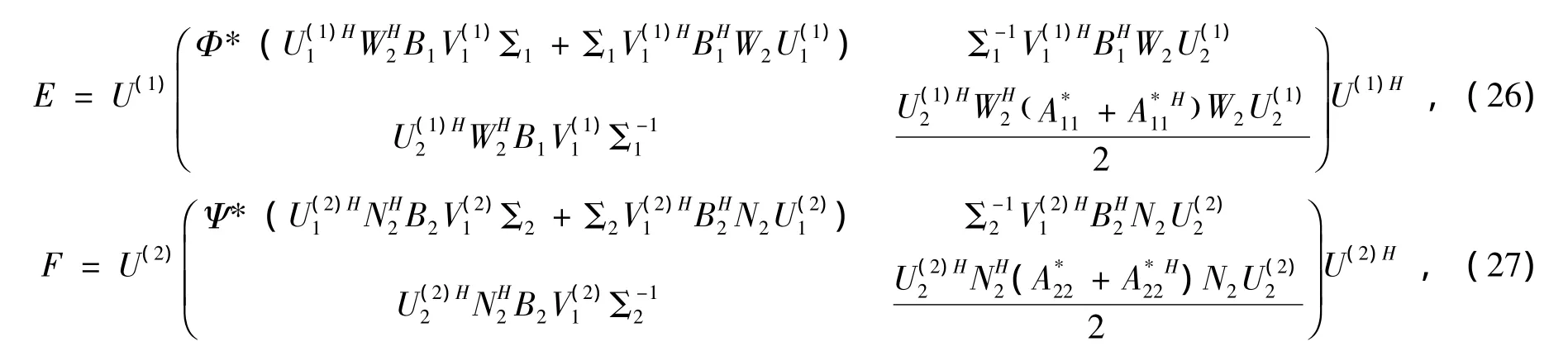
证 由 (17)、(18)、(19)式不难证明，问题Ⅰ的解集合SX，B是Hilbert空间Cn×n中的一个闭凸集。因此，对于任意给定的矩阵A*∈Cn×n，由逼近定理可知，在SX，B中存在惟一的最佳逼近。

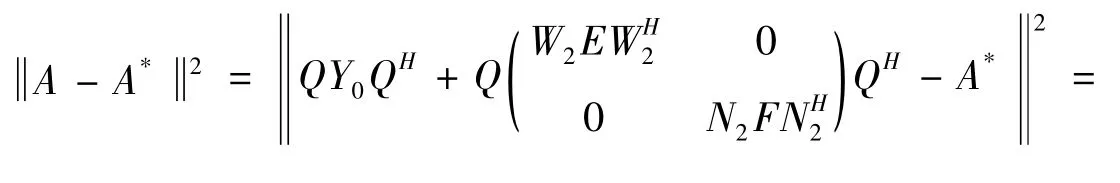
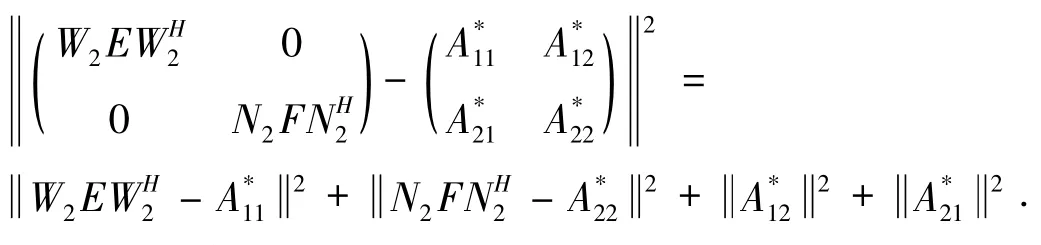
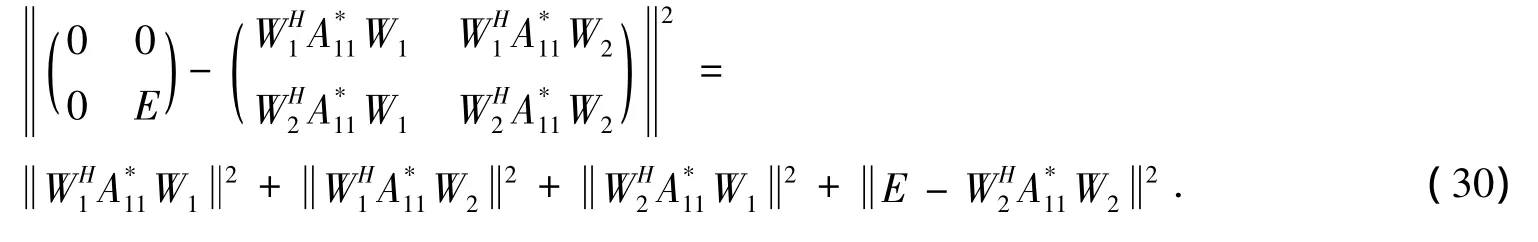
且由 (18)式得到

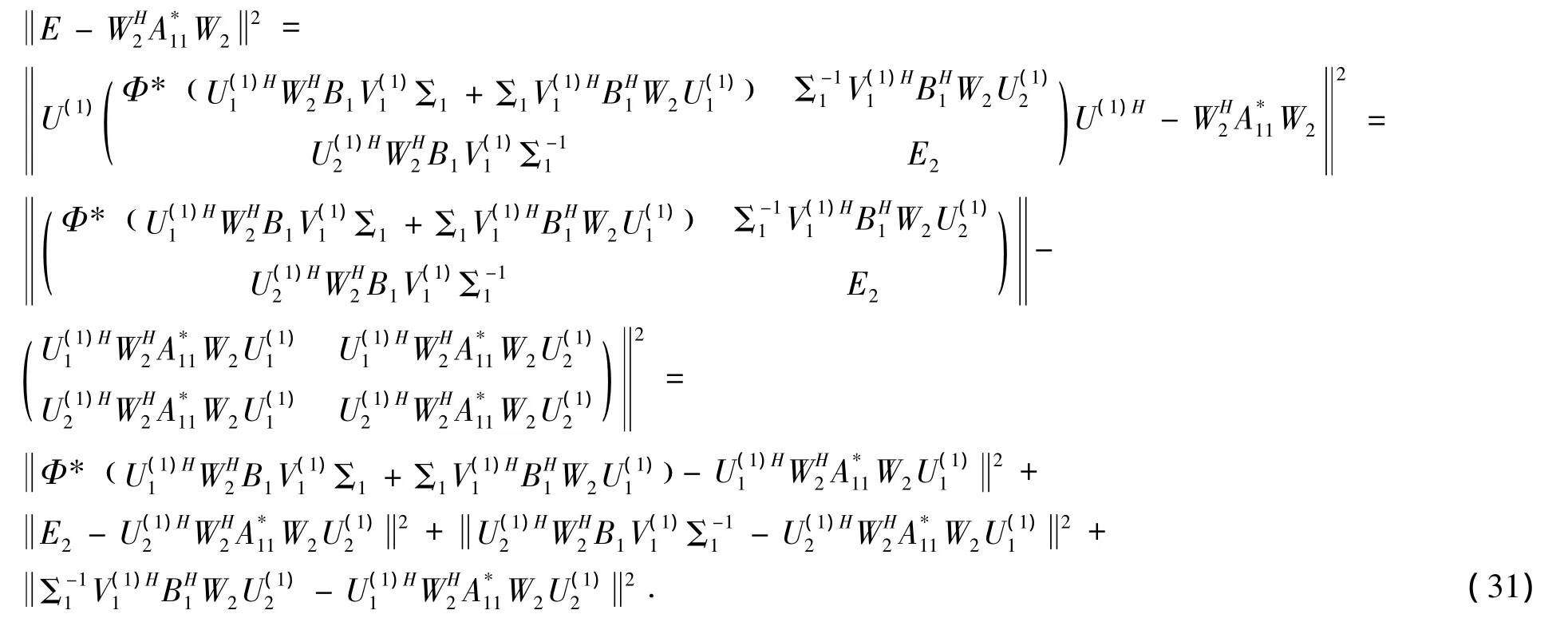
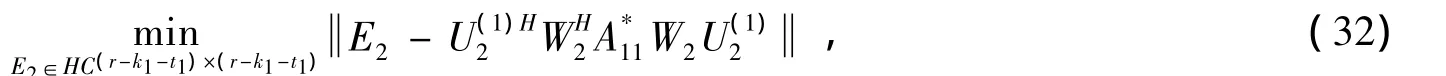
由引理5可知 (32)的解为

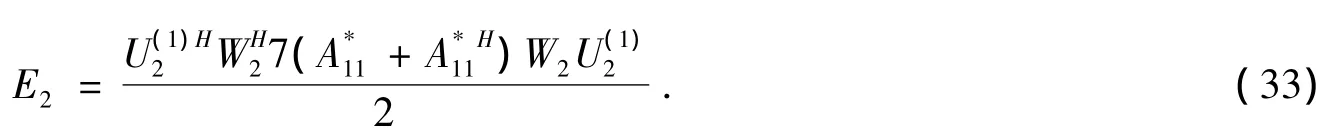
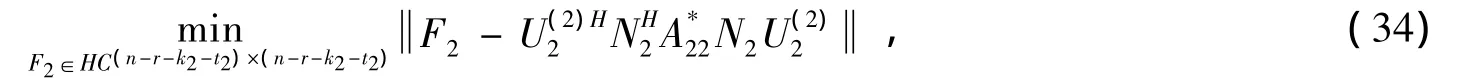
同样由引理5可知 (34)的解为

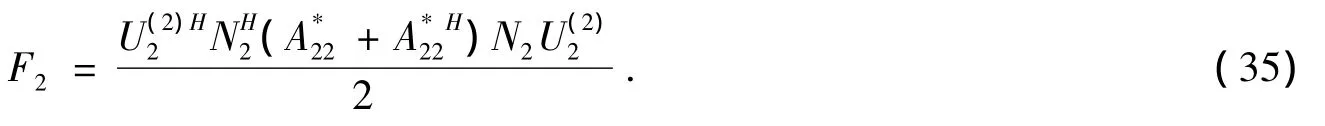
分别将 (33)、(35)代入 (18)、(19)式即可得到问题Ⅱ的解 (25)。证毕。

［1］孙继广．实对称矩阵的两类逆特征值问题［J］．计算数学，1988(3):282－290．

［2］戴华．线性流形上实对称矩阵最佳逼近［J］．计算数学，1993(4):478－488．

［3］廖安平，郭忠．线性流形上实对称半正定矩阵的一类逆特征值问题［J］．计算数学，1996(3):279－284．

［4］周富照，胡锡炎，张磊．线性流形上对称正交对称矩阵逆特征值问题［J］．计算数学，2003，25(3):281－292．

［5］张磊，谢冬秀．一类逆特征值问题［J］．数学物理学报，1993，13:94－99．

［6］张忠志，胡锡炎，张磊．线性流形上反埃尔米特广义汉密尔顿矩阵的最小二乘问题与最佳逼近问题［J］．数学物理学报，2006，26 A(6):978－986．

［7］谢冬秀．线性流形上的逆特征值问题［J］．高等学校计算数学学报，1993(4):374－380．

［8］赵丽君，胡锡炎，张磊．线性流形上复对称矩阵的最小二乘问题［J］．工程数学学报，2008，25(4):605－610．

［9］曹建胜．线性流形上的两类矩阵的最佳逼近［J］．计算数学，1998，20(2):147－152．

［10］Xie D X．least-squares solution for inverse Eigenpaitrpobem of nonnegative definite matrices［J］．Computers and Mathematics with Applications，2000，40:1241 －1251．

［11］Deng Y B，Hu X Y，Zhang L．The symmetric and symmetric positive semidefinite solutions of linear matrix equationBTXB=Don linear manifolds matrix［J］．Numercial Mathematics:A Journal of Chinese Universities，2003，12(2):186 －192．

［12］Fan K，Hoffman J A．Some metric inequalities in the space of matrices［J］．Proc Amer Math Soc，1955(6):111 －116．