关联运输调度问题的混合混沌量子算法研究

黄戈文 蔡延光 汤雅连

(1．嘉应学院 信息网络中心，广东梅州 514015;2．广东工业大学 自动化学院，广州 510006)

VRP［1－2］自1959年Dantzig和Ramser首先提出以来就引起了人们的高度重视。VRP的实用性强，应用广泛。车辆路径问题一般定义为:对一系列送货点和收货点，组织适当的行车路线，使车辆有序地通过它们，在满足一定的约束条件 (如货物需求量、发送量、送发货时间、车辆容量限制、行驶里程限制、时间限制等)下，达到一定的目标 (如路程最短、费用极小、时间尽量少、使用车辆数尽量少等)。在现实生活中存在这样的情况，不同客户需要多种零件商品，而这些零件商品由于性质、特征和用途的差异，又存在某种联系，即存在货物性质关联性，客户常常为了保证其需求不受影响而将所有的零件商品供货交付给一个物流运输公司来为其配货，将关联的货物配套运输更有利于后期的运作或经营，如一台手机的组件必须包括一个充电器，一个液晶屏、手机按键、外壳、电池等，一个螺栓对应一个螺钉，它们存在某种数量关系，客户的这种需求我们称之为需求关联。零件商品在被客户使用，即在加工组成成品的过程中，零件的使用也有一定的先后顺序，我们称零件商品具有时间关联性。这时，物流公司为需要这种货物性质的客户配送货物，应该考虑怎样进行货物任务分配、车辆分配、时间分配，并寻求最优配送路线以达到最低的物流成本，上述问题我们统称为关联运输调度问题 (Incident Vehicle Routing Problem，IVRP)，此类问题在现实生活中普遍存在，因而极具现实意义。

量子进化算法 (Quantum Evolutionary Algorithm，QEA)是20世纪90年代后期新兴的一种进化算法。由于其良好的性能，已广泛应用于诸多领域，如物流运输调度、智能交通领域、网格入侵检测、网格任务调度、非线性规划等［3－4］。Mohammed A M等人［3］提出了基于量子交叉的量子遗传算法 (quantum crossover－based quantum genetic algorithm，QXQGA)对非线性规划问题求解;蔡延光等人［4］针对量子进化算法计算量大、收敛速度慢以及容易出现早熟等问题，提出混沌混合量子进化算法，并证明其可较好地应用在智能交通领域。研究车辆路径优化问题 (Vehicle Routing Problem，VRP)是研究IVRP的基础。目前，国内外采用QEA及其改进算法对VRP或其扩展问题的研究文献不少，有一定的借鉴意义。Cui L等人［5］提出了一种带混合局部搜索的改进量子进化算法 (improved quantum evolution algorithm，IQEA)对带容量约束的VRP(capacitated vehicle routing problem，CVRP)求解;Wang L等人［6］提出了一种改进量子进化算法 (Quantum－Inspired Evolutionary Algorithm，IQEA)对带时间窗的VRP(vehicle routing problem with time windows，VRPTW)求解;葛显龙等人［7］根据随机需求信息把动态配送问题转换成一系列静态配送问题，设计基于并行节约算法动态插入随机需求信息的混合量子遗传算法，对动态模型实时再优化;之后，葛显龙等人［8］又采用量子比特位设计染色体结构，改进遗传算法中交叉与变异算子，避免优秀基因被破坏，设计快速寻优机制与最优保留机制，增强求解效率对以配送总费用最小为优化目标的数学模型求解;Zhang J等人［9］提出了一种自适应网格多目标量子进化算法 (multi－objective quantum evolutionary algorithm，MOQEA)对带客户满意度的多目标VRP(multiobjective vehicle routing problem considering customer satisfaction，MVRPCS)求解;Michallet J等人［10］研究了非常严格的带时间窗的周期性VRP，并提出了混合整数线性模型和多起点迭代局部搜索算法;Crispin A等人［11］提出了一种量子模拟算法对带容量约束的VRP求解;Zheng T等人［12］提出了量子差分进化算法对调度问题求解;Zhou L等人［13］针对传统的遗传算法不能保证收敛到最优解的最大概率，提出了对小规模求解具有快速收敛和良好搜索能力的量子遗传算法，对VRP求解;Ning T等人［14］结合量子粒子群优化算法和模拟退火算法，提出了混合量子粒子群优化算法对带时间窗的VRP求解;彭典军［15］在其硕士论文中，主要研究了一种量子进化算法在车辆路径问题中的应用，具体求解了有能力约束车辆路径问题、开放式车辆路径问题、动态网格车辆路径问题、动态需求车辆路径问题;刘勇等人［16］为求解给定期限条件的应急设施选址问题，将量子个体作为博弈者参与到竞争决策中，利用量子位、叠加态等理论提高竞争群体多样性，缩小群体规模，提出了一种量子竞争决策算法;宁涛［17］在其博士论文中，提出混合量子粒子群优化算法对带时间窗车辆路径问题求解;提出模拟退火算法与量子算法对不确定需求车辆路径问题的数学规划模型求解;结合精英量子均值和混沌扰动理论的量子进化算法对带同时取送货需求的车辆路径问题求解;蔡蓓蓓等人［18］构造了一种混合量子遗传算法，即在传统量子遗传算法随机全局搜索的基础上引入一个免疫算子，通过该算子的局部搜索实现线路内次序的再优化;李川［19］在其硕士论文中，对随机需求的车辆路径问题进行研究，通过设计不同混合量子进化算法对建立的带时间窗和基于模糊预约时间的多目标问题模型求解;任伟［20］提出了一种混合量子免疫进化算法对带时间窗的车辆调度问题求解;吴斌等人［21］针对量子进化算法中旋转角取值的离散性使其解空间的搜索具有跳跃性，提出了基于混沌理论的精英均值计算旋转角算法，对具有同时集送货需求车辆路径问题求解;赵燕伟等人［22］针对带时间窗的随机需求车辆路径问题，建立了基于模糊满意度的多目标数学规划模型，提出了一种基于量子进化算法和粒子群算法分段优化的方法求解Pareto解;李熠等人［23］提出了一种新的混合量子优化算法，即量子蚁群算法对旅行商问题求解。以上学者或研究人员都取得了不错的成果。IVRP由蔡延光教授首次提出，相关文献还相当有限，且同时考虑关联特征、载重约束、多车场多车型、车场与客户硬时间窗等因素的IVRP的研究文献还没有发现，本文提出混合混沌量子进化算法对该问题求解。

1 问题描述及数学模型

1.1 问题描述

有 i个客户 (1，2，…，l)，第 i个客户的需求量为 gi(i=1，2，…，l)，m(m=1，2，…，M)个车场，车辆装载货物后，配送给相应的客户。假设客户i所需货物有θ种，即该客户的货物种类可表示为，这θ种货物之前的需求关系可表示为，则存在种数量关系，比如，关系式之一，，即表示个货物就需要与个货物关联配送。车场m有h(h=1，2，…，H)种车型的货车k(k=1，2，…，K)辆，每种车型车辆的载重为qh，已知qh，客户硬时间窗为［eti，lti］，假定一个客户所有货物的送货时间窗一致。Ti表示车辆到达i的时间。不考虑装卸货时间。以表示车场m中车型h的车辆k从i到j的单位运输成本 (距离、费用、时间等)，路径具有对称性，即。车型h的车辆k从客户i到j之间的距离为，车辆最大行驶里程约束为Dmax。为车辆从车场实际出发的时间，为车辆从返回原车场的时间，车场硬时间窗［etm，ltm］。v为通过交通数据拟合的平均速度。目标函数为考虑路况约束、载重约束、多车场多车型、客户与车场硬时间窗等情况下，满足客户需求，并使总成本最小。

1.2 建立数学模型

假设客户编号为1，2，…，l，车场编号为l+m。决策变量如下:

目标函数:

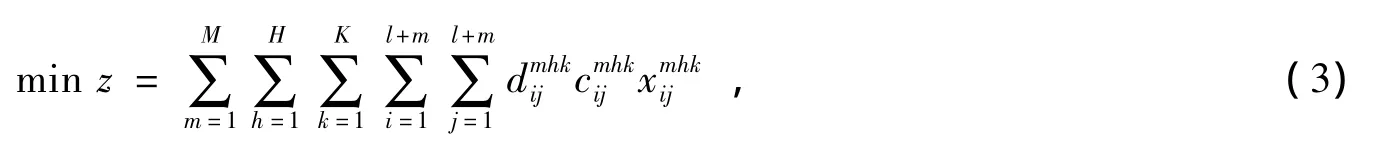
约束条件:

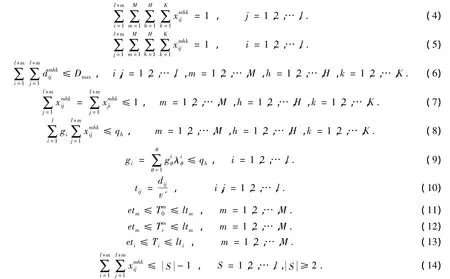
式 (3)为目标函数，表示总成本最小。式 (4)和式 (5)表示每个客户只能由某车场某车型中的一辆车服务。式 (6)表示车辆的行驶里程约束。式 (7)表示车辆从所在的车场出发，完成配送任务后，回到原车场。式 (8)和式 (9)表示每辆车所运送的货物重量不能超过此类型车辆的载重限制。式 (10)tij表示i到j的行驶时间。式 (11)－式 (12)表示车辆出发时间和返回时间必须严格遵守车场时间窗。式 (13)表示车辆送货时间严格遵守客户时间窗。式 (14)消除了车辆不是从车场出发的现象。

2 算法设计

本文采用实数对个体进行编码，与文献［4］的方法一致，采用混沌初始化方法产生初始种群，采用简单量子旋转门更新当前种群中的非最优个体，设计基于目标函数梯度信息和混沌变换序列的量子旋转门更新当前种群中的最优个体，采用混沌变异策略抑制早熟现象，提出了混合混沌量子进化算法。

2.1 编码

设X=(x1，x2，…，xn)T为所求问题模型的可行解，则对任意xi(i=1，2，…，n)，存在唯一实数θi∈［0，1］使 (15)成立，显然，θi与xi是一一对应的。

2.2 产生初始种群

设种群规模为 N ，随机生成 n 个实数 θ1，i，0 ＜ θ1，i＜ 1 ，θ1，i≠0.5 ，i=1，2，…，n 。对每个 i(i=1，2，…，n)，把 θ1，i作为 Logistic 映射的初始值，产生第 i个混沌序列 {θ2，i，θ3，i，…，θN，i}，如式 (16)所示，其中，j=1，2，…，N 。

2.3 非最优个体更新策略

采用简单量子旋转门对当前种群中的非最优个体进行更新。设全局最优个体为B=(θ1b，θ2b，…，θnb)T，即进化到目前为止的最优个体，Θ =(θ1，θ2，…，θn)T为当前种群中的任一非最优个体。当前种群中的最优个体是指当前种群中对应的目标函数值最小的个体，Θ的第i个基因θi的量子旋转门的旋转角Δθi按式 (17)选取，其中θ0为基本旋转角，且0＜θ0＜1。

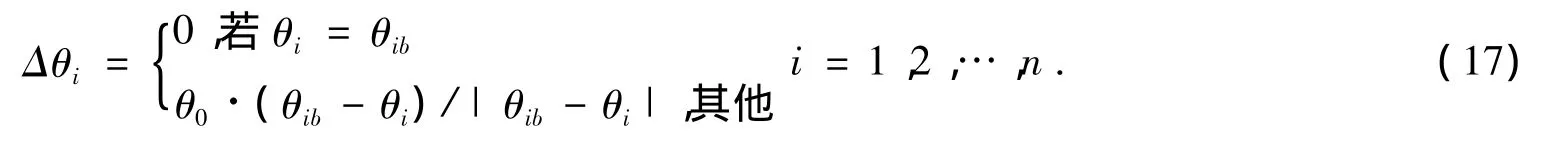
令

2.4 最优个体更新策略

基于目标函数的梯度信息和混沌变换序列，构造量子旋转门更新当前种群中的最优个体。设preGen为当前进化代数，maxGen为最大进化代数，m为解连续为得到改进 (即无效进化)的进化代数，无效进化代数的上限为M(预先给定的正整数)，假定进化尚未结束且无效进化代数未达到上限 (即preGen＜maxGen，m ＜M)。设Θ =(θ1，θ2，…，θn)T为当前种群中的最优个体。接着，对Θ进行更新，当求解最小值时，只有沿着与目标函数负梯度方向成锐角的方向搜索，目标函数值才有可能下降。为此，根据目标函数的梯度信息设计量子进化扰动参数βi，i=1，2，…，n，βi按式 (20)选取，其中▽f(θi)为f在Θ处对θi的偏导数，若f的偏导数不存在，则用f在Θ的某个充分小邻域内的任意点对θi的函数值变化率来代替，D为预先给定的大于1的常数。

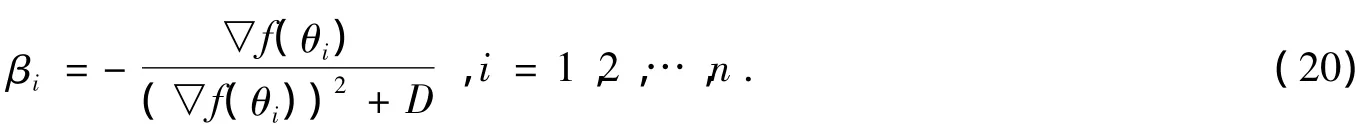
Θ 的第i个基因 θi的量子旋转门的旋转角 Δθi按式 (21)选取，其中 θ*i=4θi(1 － θi)(i=1，2，…，n)是Logistic映射产生的混沌序列。

θ'i如式 (18)所示，Θ的第i个基因按式 (19)更新，其中θi″是Θ的第i个基因的新值。

通过此方法，当前种群中的最优个体一般会沿着目标函数负梯度方向成锐角的方向进化，有利于引导整个种群朝着全局最优解的方向进化。

2.5 抑制早熟策略

假定进化尚未结束且无效进化代数达到上限，则意味着进化陷入局部最优，出现了早熟现象。采用Logistic映射对当前种群全部个体的基因进行混沌变异，以改变种群的个体分布，避免早熟现象。设(θk1，θk2，…，θkn)T为当前种群的第k个个体，k=1，2，…，N 。个体k的第i个基因按式 (22)更新，其中θ'ki为个体k的第i个基因的新值。

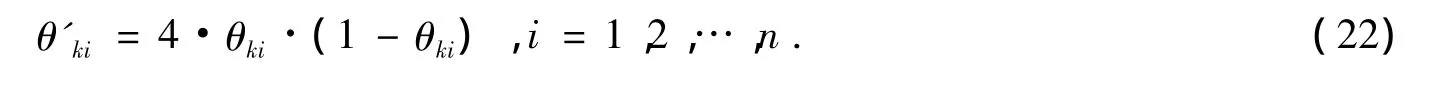
2.6 算法流程

1)设定参数:种群规模N，最大进化代数maxGen，正常数D，最大无效进化代数M，基本旋转角 θ0。

2)初始化种群:置进化代数preGen=0，无效进化代数m=0，按2.2节方法产生初始种群。

3)对种群中的所有个体按式 (1)解码得到对应的可行解，找出当前种群中的最优个体。

4)若preGen=0，置当前种群中的最优个体为全局最优个体B(如果当前种群中的最优个体不止一个，则任选一个作为全局最优个体，下同)。

5)若preGen＜maxGen，转至下一步;否则输出全局最优个体B对应的解及对应的目标函数值fB，算法结束。

6)对于preGen＞0，若当前种群中的最优个体对应的目标函数值小于fB，置当前种群中的最优个体为B，并置m=0;否则置m=m+1。

7)采用2.3节所述方法更新当前种群中的非最优个体。

8)如果m＜M，采用2.4节方法对当前种群中的最优个体进行更新;否则按2.5节所述方法对当前种群中的每个个体基因进行混沌变异。

9)preGen＜preGen+1，转步骤3)。

3 算例仿真

3.1 算例

以http://www.bernabe.dorronsoro.es/vrp/网站上的C101的50个客户点位置作为某物流公司带服务的客户位置，原车场作为第1个车场，调换原车场的纵坐标和横坐标位置，作为第2个车场。车场信息表如表1所示，客户信息表如表2所示，这些客户主要需要两大类货物 (I和II)或者倾向于某一类，其中每类货物有多种型号。每个车场 (配送中心)都有这两大类货物。每辆车的最大配送里程为180个里程单位。客户26、19、49、40、20及22的时间窗为 ［8∶00 10∶00］，其余客户的时间窗为［8∶00 11∶30］。为保证模型有可行解，将两个车场的时间窗设为 ［8∶00 12∶00］，车辆平均速度为50个速度单位。

表1 车场信息

表2 客户信息

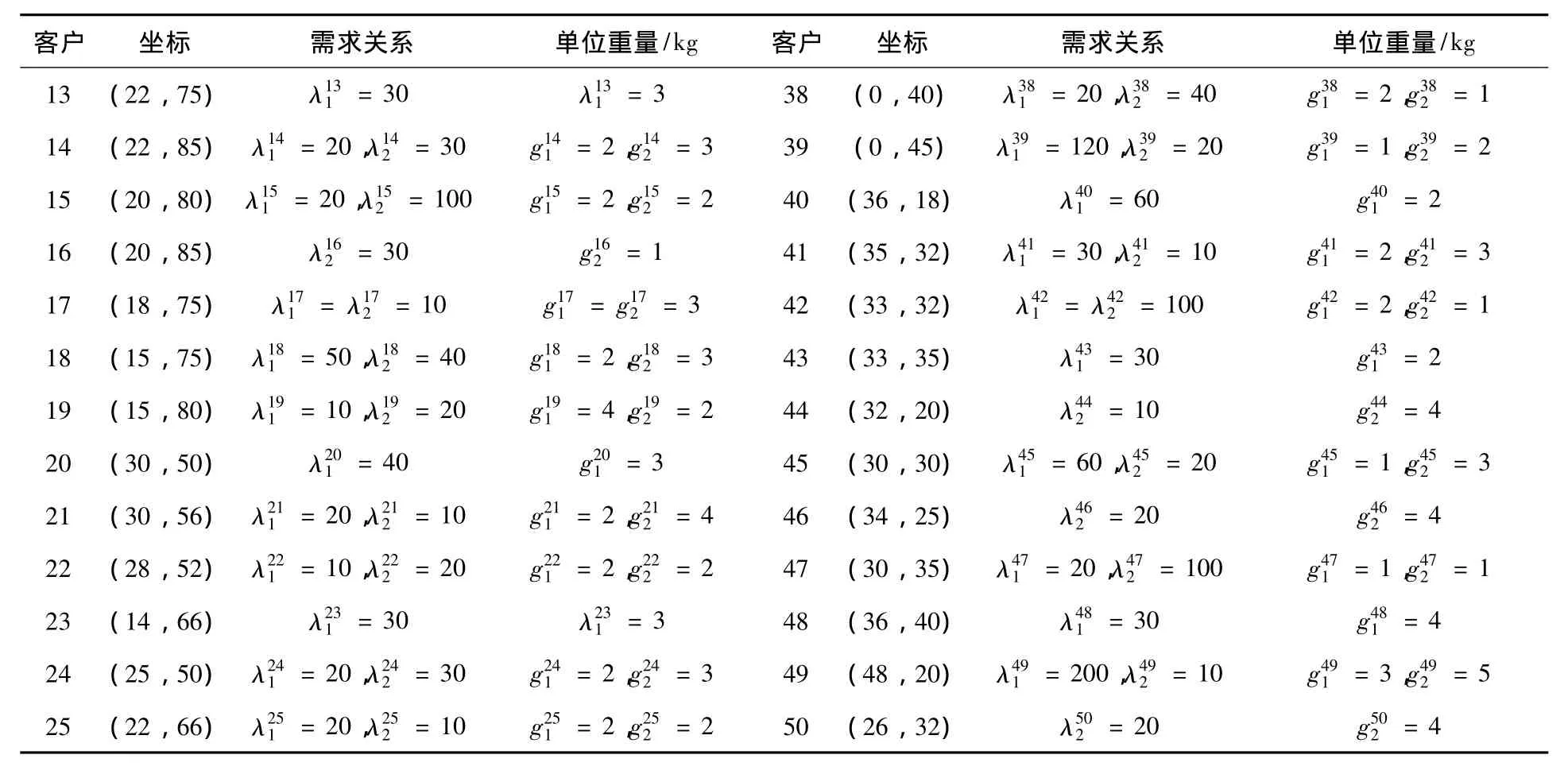
客户 坐标 需求关系 单位重量/kg 客户 坐标 需求关系 单位重量/kg 13 (22，75) λ113 =30 λ113 =3 38 (0，40) λ318 =20，λ328 =40 g318 =2，g328 =1 14 (22，85) λ114 =20，λ124 =30 g114 =2，g124 =3 39 (0，45) λ319 =120，λ329 =20 g319 =1，g329 =2 15 (20，80) λ115 =20，λ125 =100 g115 =2，g125 =2 40 (36，18) λ410 =60 g410 =2 16 (20，85) λ126 =30 g126 =1 41 (35，32) λ411 =30，λ421 =10 g411 =2，g421 =3 17 (18，75) λ117 = λ127 =10 g117 =g127 =3 42 (33，32) λ412 = λ422 =100 g412 =2，g422 =1 18 (15，75) λ118 =50，λ128 =40 g118 =2，g128 =3 43 (33，35) λ413 =30 g413 =2 19 (15，80) λ119 =10，λ129 =20 g119 =4，g129 =2 44 (32，20) λ424 =10 g424 =4 20 (30，50) λ210 =40 g210 =3 45 (30，30) λ415 =60，λ425 =20 g415 =1，g425 =3 21 (30，56) λ211 =20，λ221 =10 g211 =2，g221 =4 46 (34，25) λ426 =20 g426 =4 22 (28，52) λ212 =10，λ222 =20 g212 =2，g222 =2 47 (30，35) λ417 =20，λ427 =100 g417 =1，g427 =1 23 (14，66) λ213 =30 λ213=3 48 (36，40) λ418=30 g418 =4 24 (25，50) λ214 =20，λ224 =30 g214 =2，g224 =3 49 (48，20) λ419 =200，λ429 =10 g419 =3，g429 =5 25 (22，66) λ215 =20，λ225 =10 g215 =2，g225 =2 50 (26，32) λ520 =20 g520 =4

3.2 参数设置及结果分析

在Intel(R)Core®i5 CPU 3.0GHz、内存为8.0G、安装系统为Windows7的PC机上采用Matlab R2010b编程实现。针对VRP模型和IVRP模型，首先采用HCQEA对这两种模型求解，然后采用另外两种算法对IVRP求解，各运行算法20次。

HCQEA参数设计:N=20，maxGen=200，D=1 000，θ0=0.005;QEA参数设计:可行解的每个分量用20个二进制位表示，群体规模m=20，maxGen=200，基本旋转角自适应遗传算法 (adaptive genetic algorithm，AGA)参数设计:种群规模m=20，最大迭代次数Gen=200，交叉概率pc=0.9，变异概率pm=0.04，采用最佳保留选择法选择算子，多点交叉，均匀变异。

图1 MDVRPHTW配送网络 (非关联)

图2 MDVRPHTW配送网络 (关联)

表3 MDVRPHTW的具体配送信息 (非关联)

表4 MDIVRPHTW的具体配送信息 (关联)

求解MDVRPHTW和MDIVRPHTW的配送网络图如图1和图2所示。具体配送信息分别如表3和表4所示，可见MDVRPHTW需要使用6辆车，MDIVRPHTW使用了5辆车，减少了一辆车的使用，且总成本降低了27.75%，所以该模型的提出是有意义的。

MDIVRPHTW的一次优化过程如图3所示，HCQEA在第110代求得的总成本为205.69个费用单位，QEA在第170代求得的总成本为213.52个费用单位，AGA在第120代求得的总成本是213.52个费用单位。可见，虽然AGA能较早收敛，可是易陷入局部最优，而HCQEA的求解速度和得到的解结果总体来说优于另外两种算法，这主要归因于引入了混合混沌搜索策略，提高了算法的收敛速度和全局搜索能力。

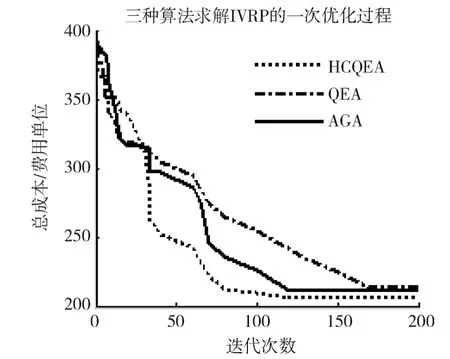
图3 MDIVRPHTW的一次优化过程

4 结语

文中提出了引入混合混沌策略的混合混沌量子进化算法。考虑了关联因素对物流配送的影响，提出了带多种扩展特征 (考虑多车型、客户和车场硬时间窗等约束)的IVRP模型，通过HCQEA、AGA和QEA对模型求解的结果相比较，证明其优越性，也体现出提出模型的有效性，研究更大规模问题模型及包含多种扩展特性 (次序关联、不对称、随机需求、多周期性、需求可拆分、同时取送货、开放式、服务优先级等)的IVRP及其求解算法将是今后的研究方向。

［1］Azi N，Gendreau M，Potvin J Y．An adaptive large neighborhood search for a vehicle routing problem with multiple routes［J］．Computers＆Operations Research，2014，41:167－173．

［2］Michallet J，Prins C，Amodeo L，et al．Multi－start iterated local search for the periodic vehicle routing problem with time windows and time spread constraints on services［J］．Computers＆ Operations Research，2014，41:196－207．

［3］Mohammed A M，Elhefhawy N A，El－Sherbiny M M，et al．Quantum crossover based quantum genetic algorithm for solving non－linear programming［C］//Informatics and Systems(INFOS)，2012 8th International Conference on．IEEE，2012:BIO －145－BIO－153．

［4］蔡延光，张敏捷，蔡颢，等．混合混沌量子进化算法［J］．系统工程理论与实践，2012，32(10):2207－2214．

［5］Cui L，Wang L，Deng J，et al．A new improved quantum evolution algorithm with local search procedure for capacitated vehicle routing problem［J］．Mathematical Problems in Engineering，2013:17．

［6］Wang L，Kowk S K，Ip W H．Design of an improved quantum－inspired evolutionary algorithm for a transportation problem in logistics systems［J］．Journal of Intelligent Manufacturing，2012，23(6):2227－2236．

［7］葛显龙，王旭，代应．基于混合量子遗传算法的随机需求车辆调度问题［J］．系统工程，2011，29(3):53－59．

［8］葛显龙，许茂增，王伟鑫．多车型车辆路径问题的量子遗传算法研究［J］．中国管理科学，2013，1:125－133．

［9］Zhang J，Wang W，Zhao Y，et al．Multiobjective quantum evolutionary algorithm for the vehicle routing problem with customer s atisfaction［J］．Mathematical Problems in Engineering，2012:19．

［10］Michallet J，Prins C，Amodeo L，et al．Multi－ start iterated local search for the periodic vehicle routing problem with time windows and time spread constraints on services［J］．Computers＆ operations research，2014，41:196－207．

［11］Crispin A，Syrichas A．Quantum Annealing Algorithm for Vehicle Scheduling［C］//Systems，Man，and Cybernetics(SMC)，2013 IEEE International Conference on．IEEE，2013:3523－3528．

［12］Zheng T，Yamashiro M．Quantum －inspired differential evolutionary algorithm for permutative scheduling problems［M］．Rijeka，Croatia:In-Tech．Evolutionary Algorithms，2011，109 －132．

［13］Zhou L，Li R，Li Q．Research on Vehicle Routing Problem Based on Quantum Genetic Algorithm［C］//ICLEM 2010:Logistics For Sustained Economic Development:Infrastructure，Information，Integration．ASCE，2010:2965－2971．

［14］Ning T，Guo C．Using hybrid quantum algorithm to solve VRPTW［C］//Intelligent Control and Information Processing(ICICIP)，2012 Third International Conference on．IEEE，2012:59－62．

［15］彭典军．车辆路径问题的量子进化算法研究［D］．杭州:浙江工业大学，2009．

［16］刘勇，马良，宁爱兵．给定限期条件下应急选址问题的量子竞争决策算法［J］．运筹与管理，2011，20(3):66－71．

［17］宁涛．混合量子算法在车辆路径问题中应用的研究［D］．大连:大连海事大学，2013．

［18］蔡蓓蓓，张兴华．混合量子遗传算法及其在VRP中的应用［J］．计算机仿真，2010，27(7):267－334．

［19］李川．基于混合量子进化算法的随机车辆路径问题的研究［D］．杭州:浙江工业大学，2011．

［20］任伟．基于量子免疫算法的车辆调度问题的优化［J］．计算机科学，2013，40(5):233－236．

［21］吴斌，钱存华，董敏，等．具有同时集送货需求车辆路径问题的混沌量子进化算法研究［J］．2010，25(3):383－387．

［22］赵燕伟，李川，张景玲，等．一种新的求解多目标随机需求车辆路径问题的算法［J］．计算机集成制造系统，2012，18(3):523－530．

［23］李熠，马良．用量子蚁群算法求解大规模旅行商问题［J］．上海理工大学学报，2012，34(4):355－358．