机载PMSM伺服作动系统约束反演控制

陈晓雷 林 辉 吕帅帅

(西北工业大学自动化学院 西安 710129)

0 引言

机电伺服作动系统是多电飞机的核心组成部分［1］。近年来，随着功率电传技术的发展，尤其是高压直流电源系统的采用，使得大功率机电作动系统在飞机上的应用成为现实，弥补了传统液压作动机构的缺陷，极大地提高了飞机的操纵和控制性能［2］。机电作动系统中，伺服电动机及控制器是关键所在。永磁同步电动机(Permanent Magnet Synchronous Motors，PMSM)具有转矩脉动小、调速范围宽以及功率密度高等优势，在航空领域具有良好的发展前景。

然而，PMSM 本身具有多变量、非线性及强耦合等特点［3］，而机载作动伺服系统的工作环境尤为严酷，环境温度变化较大，导致电动机参数(如绕组电阻、永磁体性能和粘性摩擦系数等)会有较大变动，在不同飞行状态下也存在负载变化，以上原因导致实现高精度位置控制难度较大。此外，与常规位置伺服系统不同，机载作动系统作为飞控系统的子系统，其输出量即舵面偏角与飞机飞行姿态息息相关，若舵面偏转角误差过大，即使子系统稳态性能可以保证，但必然对飞控系统的机动性能和稳定性产生负面影响。为保障可靠性，通常对舵面偏角误差的上下界做出严格限制。现有PMSM 位置伺服控制方法包括分数阶控制［4］、自适应控制［5］、滑模控制［6，7］以及LPV 控制［8］等。文献［4，5］所提控制策略不足之处在于控制器结构或参数自适应律复杂。文献［6-8］的优势是不严格依赖精确数学模型，控制算法可保证系统渐进稳定，但缺陷是系统动态性能依赖参数整定，控制精度难以得到保障。

长久以来，Lyapunov 函数被视为非线性系统稳定性分析的有力工具。文献［9］提出并完善了反演控制(Backstepping Control)方法，通过设计满足需求的中间虚拟控制量和分项控制Lyapunov 函数(Control Lyapunov Function，CLF)，反向递推获得反馈控制律和整体CLF。该策略将CLF 构造和镇定控制律设计紧密结合，适用于严格反馈系统(如PMSM 位置伺服系统)。文献［10］提出一种反演滑模控制策略。文献［11］提出一种积分反演控制策略，采用自适应关联观测器估算转子位置及转速。文献［12］提出一种自适应反演控制策略，采用反演观测器实现无传感器控制。文献［13］针对PMSM 参数时变问题，设计参数自适应律及反演控制器。然而，常规反演控制只能保证伺服系统的稳定性，无法处理输出误差约束问题。近年来，通过对二次型结构CLF 的改进，该问题已取得一定研究成果。文献［14］针对含状态约束的Brunovsky标准型系统，以约束区间作为定义域，构造对数型及反正切型障碍函数作为CLF 实现反演控制。在文献［14］的基础上，文献［15］将此类基于障碍函数的CLF 定义为障碍Lyapunov 函数(Barrier Lyapunov Function，BLF)，针对严格反馈系统进行反演设计，可保证系统输出有界。

本文在以上研究的基础上，借鉴文献［15］的思想，提出一种基于对称BLF 的反演控制策略。为补偿负载扰动和参数变化，消除未建模动态引起的稳态误差，在控制设计环节增加积分项［16］。通过Lyapunov方法证明闭环系统的全局渐进稳定性，闭环系统信号一致有界，跟踪误差可收敛到原点较小邻域，且控制过程中舵面跟踪误差始终保持在约束区间内。通过仿真和实验验证了本文方法的有效性。

1 机载PMSM 伺服作动系统模型

机电作动伺服系统的目的是实现舵面对给定位置指令的准确跟踪。为提高系统可靠性，降低故障率，通常采用余度结构，在结构设计中采用位置控制器、两套PMSM 电动机及驱动器并行工作的方式，通过差动周转轮系实现驱动轴机械运动的合成，输出低转速、高扭矩的动力，作用到传动链实现舵面收放。简单起见，本文考虑正常工况，假设两套电动机参数相同，则转速相同时不存在力纷争问题。

假设磁路不饱和，不计磁滞和涡流损耗影响，气隙磁场呈正弦分布，定子为三相对称绕组，转子无阻尼绕组。隐极式PMSM 的数学模型为［17］

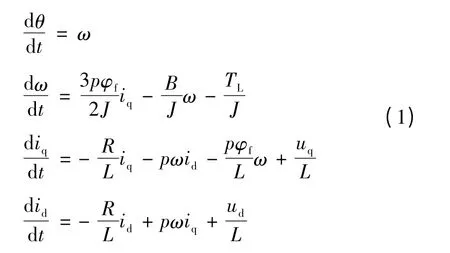
式中:θ 为转子机械角位移;ω 为转子机械角速度;p 为磁极对数;φf为转子永磁体在定子上的耦合磁链;J 为折算到电动机轴上的等效转动惯量;id、iq分别为定子电流矢量的d、q 轴分量;B 为粘滞系数;TL为负载转矩;R 为绕组电阻;L 为绕组电感;uq、ud分别为定子电压矢量的d、q 轴分量。

不考虑传动链的间隙与弹性变形，θ 与舵面转角φ 的关系为

式中kr为传动链的减速比。

TL与空气特性、飞机飞行马赫数、飞行高度、飞行攻角以及舵面转角等均相关，简单起见，认为TL与φ 呈线性关系，为弹性负载

式中:T0为舵面处于收拢状态时的负载转矩;kθ为线性比例系数。

取状态变量［xi］=［φ，ω，iq，id］，联立式(1)～式(3)，可得PMSM 伺服作动系统数学模型为

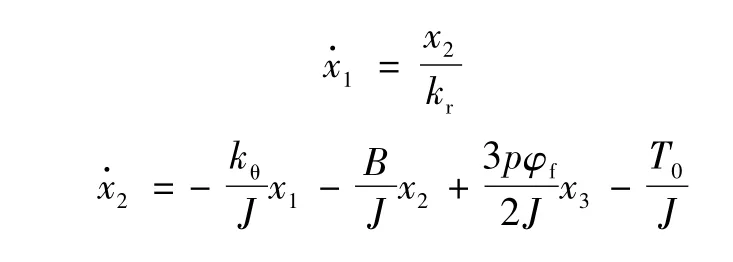
2 控制器设计

对式(4)描述的严格反馈非线性系统［18］，提出一种反演控制方法，通过设计障碍Lyapunov 函数，实现对舵面转角φ 的约束，并证明系统的稳定性。

2.1 基于BLF 的反演控制器设计

反演控制将Lyapunov 函数的选取与控制器设计相结合，将非线性系统分解成若干不超过系统阶数的子系统，然后为每个子系统设计CLF 和虚拟控制量，逐层修正算法来设计镇定控制器，最终完成控制律的设计，实现全局调节和跟踪。本文在虚拟控制中引入误差的积分项，利用积分作用消除稳态误差，与常规反演控制不同之处在于选取BLF 而非二次型作为Lyapunov 函数。具体设计步骤如下:

1)设φ*为舵面期望转角，设舵面转角容许误差范围为(- kb，kb)，定义跟踪误差为:，，其中、为虚拟控制量。

引入输出误差的积分，记为

对式(5)求导，有

对z1求导，并将式(4)代入，可得

选取Lyapunov 函数

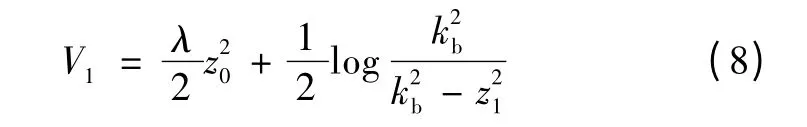
由文献［15］中BLF 定义可知，V1为BLF。取x2的虚拟控制量ω*为

式中κ1＞0 为待设计的参数，对式(8)求导，得

2)由于x2并非受约束项，故而可选择二次型Lyapunov 函数作为候选函数

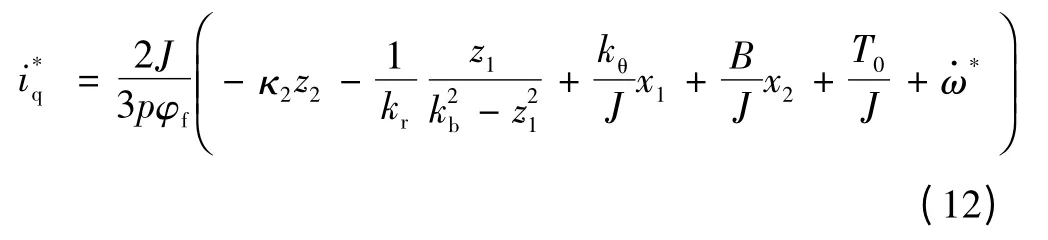
式中κ2＞0，对式(11)求导，得

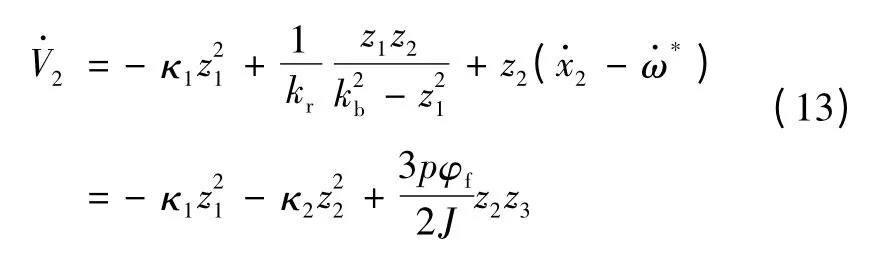
3)选择二次型Lyapunov 函数为

对式(14)求导，得

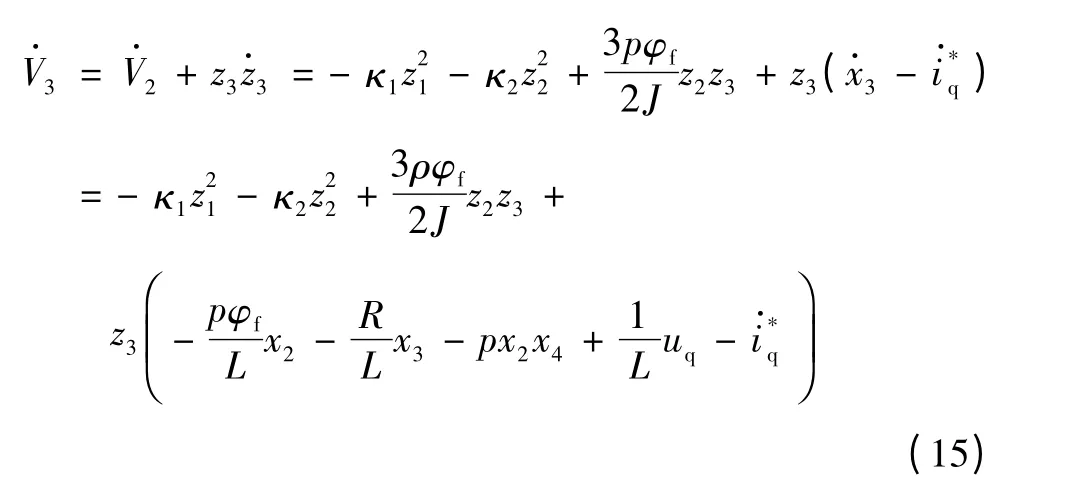
选取实际uq为

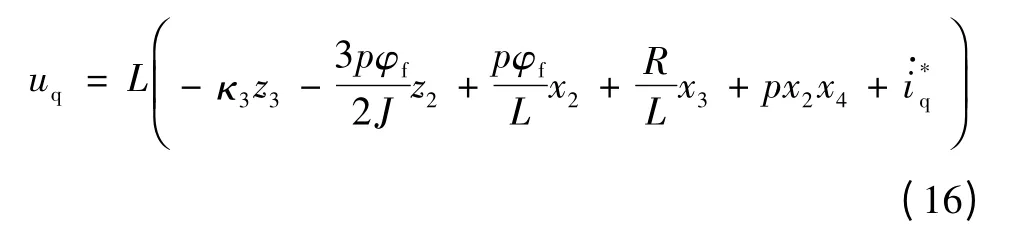
式中κ3＞0，则式(15)可化简为

4)为实现电流和速度的解耦，使转矩不受磁通电流的影响，需采用i*d=0 的控制策略。选择二次型Lyapunov 函数为

对式(18)求导，得

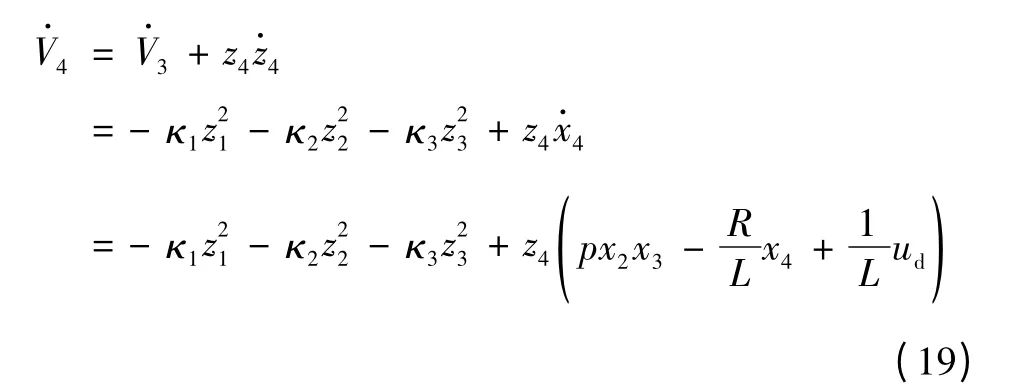
选取实际ud为

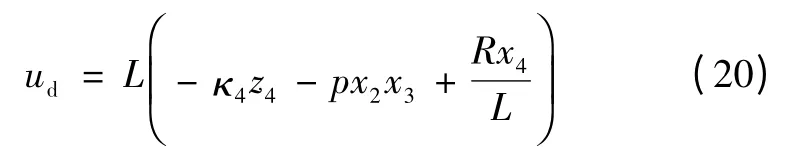
式中κ4＞0。至此完成控制律设计。PMSM 伺服作动系统反演控制结构如图1所示。

图1 PMSM 伺服作动系统约束反演控制Fig.1 Backstepping-based constraint control for PMSM Servo-Actuation System

2.2 系统稳定性证明

定理:对式(4)所示伺服作动系统，采用式(16)、式(20)反馈控制律，若舵面转角期望指令连续且三阶可导，并满足(χ1为一正数)，且初始条件}，则以下结论成立。

1)误差信号zi(t)保持在紧集Ωz内。

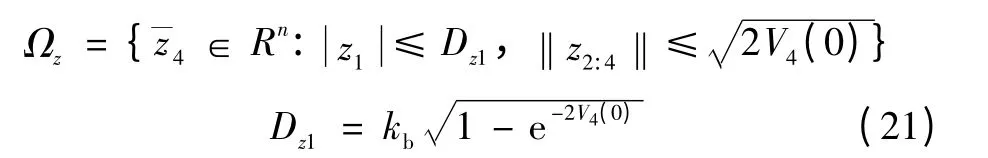
2)输出信号y(t)保持在紧集Ωy内，且严格有界。

3)所有闭环信号皆有界。

4)系统输出误差z1(t)渐近收敛到零，当t →∞，y(t)→φ*(t)。

证明:1)将式(20)代入式(19)，得

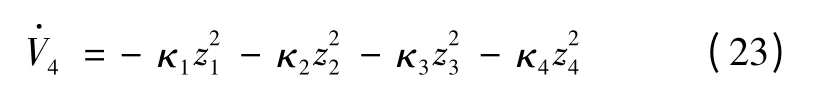
由于κi＜0(i=1，…，4)，可知，由此可知V4(t)≤V4(0)，若z1(0)∈(- kb，kb)，根据文献［15］中引理1 可知，z1∈(- kb，kb)∀t ∈［0，∞)。由式(8)可知

3)由z1(t)有界结合由式(9)可知虚拟控制量ω*有界，依此类推可知zi(t)有界，结合设计过程可知控制律uq和ud亦有界，由此可得系统闭环信号皆有界。

4)由zi(t)有界，可计算出亦有界，对式(23)求导可知有界，为一致连续，由Barbalat 引理可知，当t →∞时，→0，即zi(t)→0，可实现对舵面位置的精确跟踪。

3 仿真结果及分析

在Matlab 环境下进行数值仿真，验证本文所设计控制器的有效性。仿真参数如表1 所示。

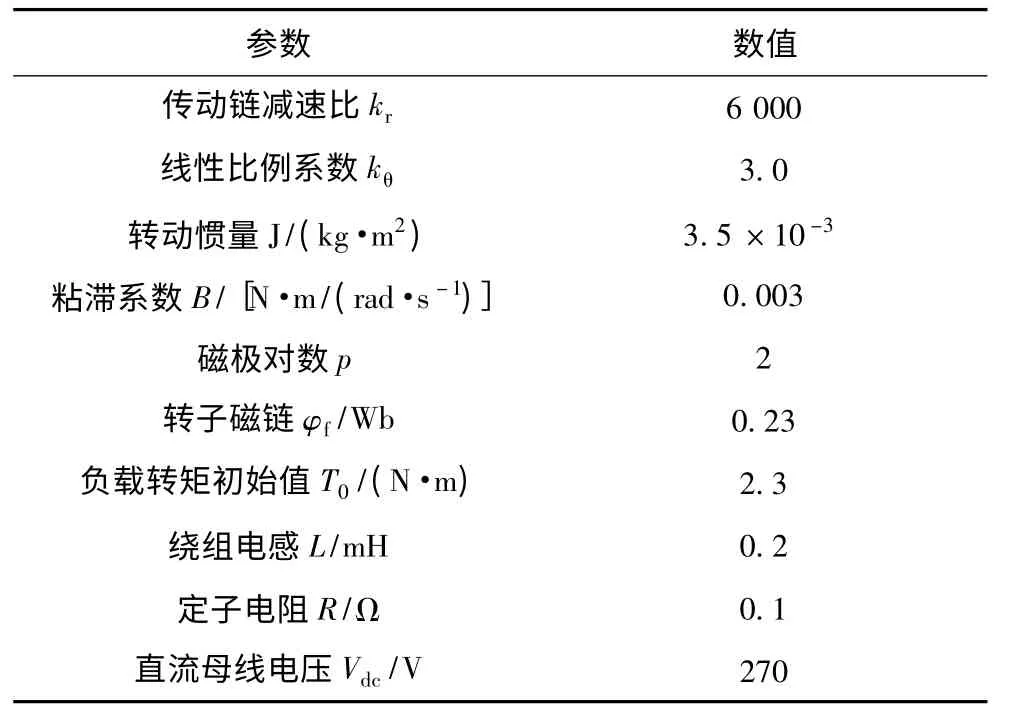
表1 伺服作动系统参数Tab.1 Parameters of servo-actuation system

舵面运动通常是绕伺服系统的输出轴作往复摆动，可近似为正弦运动，满足定理中假设条件，设置舵面转角期望指令为，结合工程实际，设计kb为1.5，即舵面偏角容许误差范围z1∈(-1．5，1．5)，控制器参数设置为κ1=κ2=3 000，κ3=κ4=500，λ=2 000。

采用本文方法控制效果如图2所示，可看出舵面位置具有较高的控制准确度，未有产生较大的超调量，z1(t)始终被约束在设定范围内，且收敛较快速，电动机实时转速较准确的逼近虚拟控制量ω*。

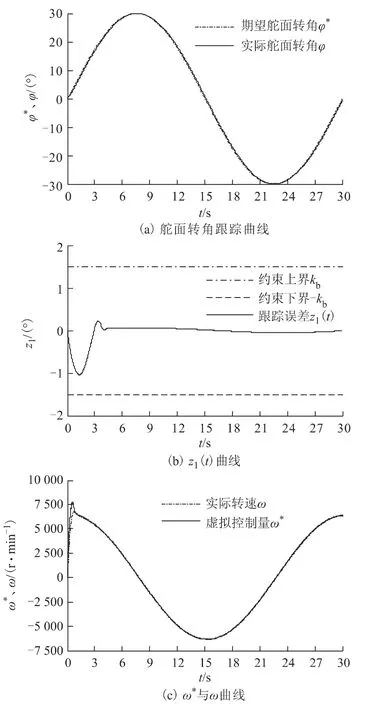
图2 本文方法控制结果Fig.2 Simulation results of proposed method

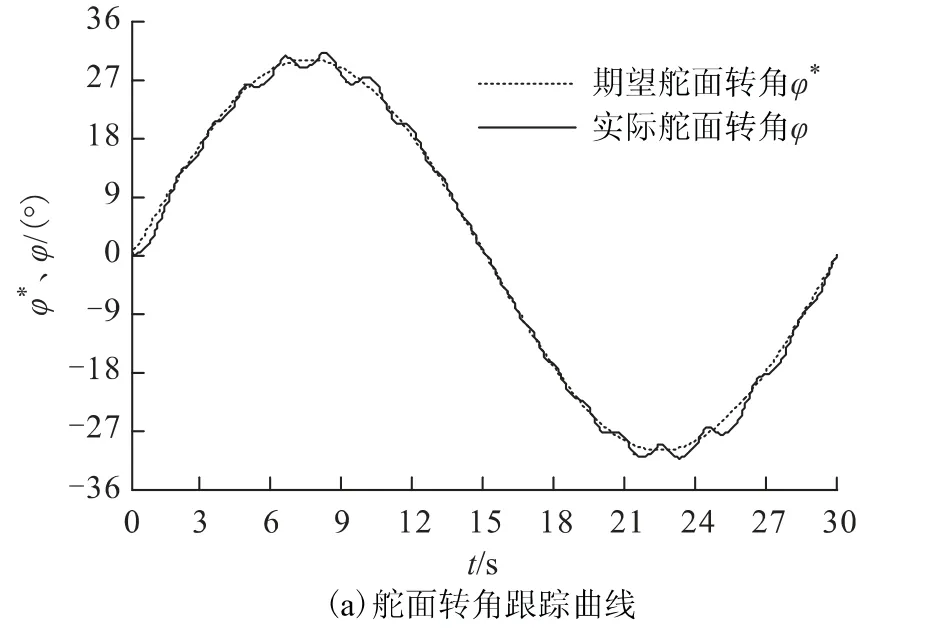
图3 常规反演方法控制结果Fig.3 Simulation results of classical backstepping method

由图3可知，常规反演控制仍能保证系统稳定性，但对系统动态性能的调节仅依赖于控制器参数的整定，对误差约束条件是无法处理的。

4 实验结果

为验证机载PMSM 伺服作动系统及控制器性能，建立实验平台如图4所示。

图4 伺服系统实验平台Fig.4 Servo-actuation system experimental platform

作动机构采用并行/主动式双余度结构，为测试PMSM 性能，实验中采用单通道控制。负载模拟器是舵面负载力矩的加载装置，能模拟随马赫数、攻角及舵偏角等参数变化的舵面负载力矩。伺服控制器采用TI TMS320F2812，逆变单元采用IGBT 组成全桥结构，通过光电编码器进行速度测量。

为验证积分反馈的作用，设计不含积分反馈的约束反演控制器。控制器设计中选择对数型BLF，V1=其余步骤与上文相同，控制器参数同仿真验证。实验结果如图5所示。

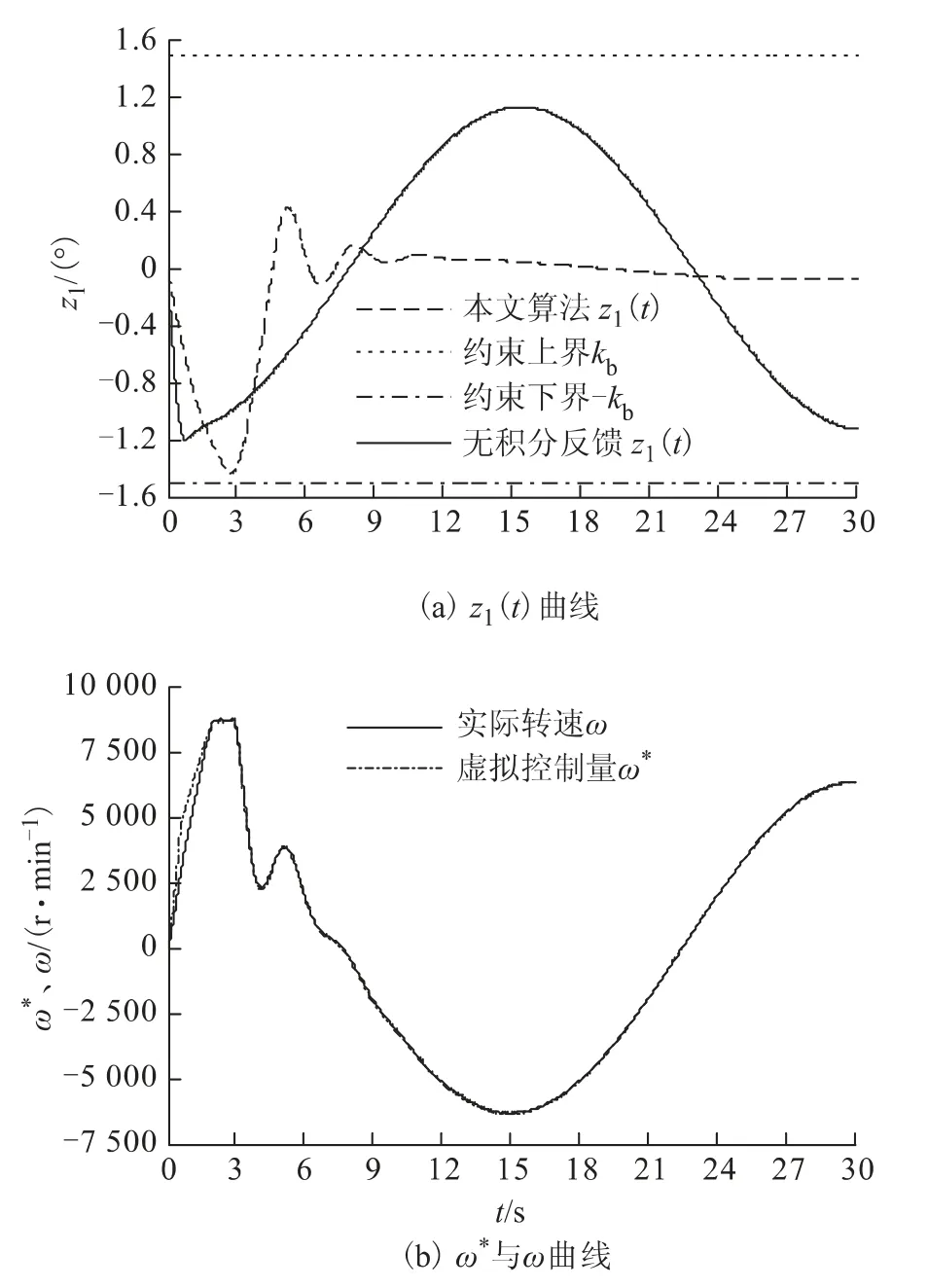
图5 本文方法实验结果Fig.5 Experimental results of proposed method

通过图5a 舵面转角误差对比结果可看出积分反馈的作用，由于作动系统中存在参数时变特性及未建模动态，积分项的引入显著提高了舵面位置跟踪精度，加快了误差信号zi(t)的收敛速度。

对比图5a 与图3b 可知，与仿真结果相比，实验结果的最大误差和误差绝对值积分显著偏大，主要考虑以下原因:数学模型中忽略了实际作动系统的非线性特性，如电动机发热导致的模型参数变化，负载模拟器存在多余力矩，舵面存在机械连接间隙非线性、摩擦非线性、同轴度误差等。由图5b 可知电动机转速能准确快速地跟踪参考转速信号。实验结果表明本文算法具有较好的鲁棒性，可保证系统的全局渐近稳定性，且可保证对超调量的有效约束。

5 结论

针对机载PMSM 伺服作动系统存在的强耦合非线性特性以及高精度控制需求，提出一种基于障碍Lyapunov 函数的积分反演控制策略，实现对输出误差的约束，证明了控制算法的收敛性，并研究了障碍Lyapunov 函数及积分项在反演控制中的作用。可得如下结论:

1)传统反演方法仅能保证PMSM 伺服作动系统稳定性，无法解决对误差量的约束问题。

2)本文方法不仅可实现伺服控制的全局渐进稳定，而且可实现对输出误差量的实时约束，通过理论证明与仿真对比可知，本文方法弥补了传统反演控制方法的不足，实现了机载伺服系统的高精度控制。

3)反演设计中引入积分项，一定程度上增强了系统的鲁棒性，对改善稳态控制品质有积极意义。

4)递推设计环节中可考虑采用有限时间滑模控制方法设计虚拟控制量，加快收敛速度，增强系统鲁棒性。

［1］ 罗战强，梁得亮．双余度机电作动伺服系统数学模型与特性［J］．电工技术学报，2014，29(1):165-173．

Luo Zhanqiang，Liang Deliang．Mathematical model and characteristics on dual-redundancy electromechanical actuation servo system［J］．Transactions of China Electrotechnical Society，2014，29(1):165-173．

［2］ 张巍，尚晓磊，周元钧，等．一种适用于航空电力作动器负载的三相PWM 整流器最大功率控制［J］．电工技术学报，2011，26(8):91-98．

Zhang Wei，Shang Xiaolei，Zhou Yuanjun，et al．A maximum power control method of three-phase voltage source rectifiers adapted to aircraft electric actuator load［J］．Transactions of China Electrotechnical Society，2011，26(8):91-98．

［3］ 黄庆，黄守道，伍倩倩，等．基于模糊自抗扰控制器的永磁同步电动机伺服系统［J］．电工技术学报，2013，28(9):294-301．

Huang Qing，Huang Shoudao，Wu Qianqian，et al．PMSM servo system based on fuzzy active-disturbance rejection controller［J］．Transactions of China Electrotechnical Society，2013，28(9):294-301．

［4］ Luo Y，Chen Y Q，Ahn H S，et al．Fractional order robust control for cogging effect compensation in PMSM position servo systems:stability analysis and experiments［J］．Control Engineering Practice，2010，18(9):1022-1036．

［5］ Kumar V，Gaur P，Mittal A P．ANN based self tuned PID like adaptive controller design for high performance PMSM position control［J］．Expert Systems with Applications，2014，41(7):7995-8002．

［6］ Qi Liang，Shi Hongbo．Adaptive position tracking control of permanent magnet synchronous motor based on RBF fast terminal sliding mode control［J］．Neurocomputing，2013，115(4):23-30．

［7］ Ghafari-Kashani A R，Faiz J，Yazdanpanah M J．Integration of non-linear H∞and sliding mode control techniques for motion control of a permanent magnet synchronous motor［J］．IET Electric Power Applications，2010，4(4):267-280．

［8］ Cauet S，Coirault P，Njeh M．Diesel engine torque ripple reduction through LPV control in hybrid electric vehicle powertrain:experimental results［J］．Control Engineering Practice，2013，21(12):1830-1840．

［9］ Krstic M，Kanellakopoulos I，Kokotovic P V．Nonlinear and Adaptive Control Design［M］．New York:John Wiley＆ Sons，1995．

［10］ 付培华，陈振，丛炳龙，等．基于反步自适应滑模控制的永磁同步电机位置伺服系统［J］．电工技术学报，2013，28(9):288-293．

Fu Peihua，Chen Zhen，Cong Binglong，et al．A position servo system of permanent magnet synchronous motor based on back-stepping adaptive sliding mode control［J］．Transactions of China Electrotechnical Society，2013，28(9):288-293．

［11］ Hamida Mohamed Assaad，Glumineau Alain，Leon de Jesus．Robust integral backstepping control for sensorless IPM synchronous motor controller［J］．Journal of the Franklin Institute，2012，349(5):1734-1757．

［12］ Morawiec M．The adaptive backstepping control of permanent magnet synchronous motor supplied by current source inverter［J］．IEEE Transactions on Industrial Informatics，2013，9(2):1047-1055．

［13］ Karabacak M，Eskikurt H I．Speed and current regulation of a permanent magnet synchronous motor via nonlinear and adaptive backstepping control［J］．Mathematical and Computer Modelling，2011，53(9):2015-2030．

［14］ Ngo K B，Mahony R E，Jiang Z P．Integrator backstepping using barrier functions for systems with multiple state constraints［C］．44th IEEE Conference on Decision ＆ Control，Seville，Spain，2005:8306-8312．

［15］ Tee K P，Ge S S，Tay E H．Barrier Lyapunov Functions for the control of output-constrained nonlinear systems［J］．Automatica，2009，45(4):918-927．

［16］ Alain Glumineau，de Leon Morales Morales．Sensorless AC Electric Motor Control-Robust Advanced Design Techniques and Applications［M］．Berlin:Springer，2015．

［17］ 许叙遥，林辉．基于动态滑模控制的永磁同步电机位置速度一体化设计［J］．电工技术学报，2014，29(5):77-83．

Xu Xuyao，Lin Hui．Integrated design for permanent magnet synchronous motor servo systems based on dynamic sliding mode control［J］．Transactions of China Electrotechnical Society，2014，29(5):77-83．

［18］ Tong Shaocheng，Liu Changliang，Li Yongming．Adaptive fuzzy backstepping output feedback control for strict feedback nonlinear systems with unknown sign of high-frequency gain［J］．Neurocomputing，2012，77(1):58-70．