基于准梯形永磁体的多相分数槽集中整距绕组永磁电动机齿槽转矩抑制

康惠林 周理兵 王 晋 彭 溪

(强电磁场工程与新技术国家重点实验室(华中科技大学)武汉 430074)

0 引言

多相分数槽集中绕组永磁电动机容错性能好、效率高，得到了广泛研究和应用［1-5］。多相分数槽集中整距绕组永磁电动机绕组系数为1［6，7］，有利于通过注入谐波电流提高功率密度，其特性值得深入研究。该电动机特性之一是存在齿槽转矩，导致转矩波动、振动和噪声，需要设法削弱。齿槽转矩的抑制方法很多，如斜槽和斜极、辅助槽、极弧系数优化以及磁极偏移、槽口宽优化、永磁体分段等［8，9］。多相分数槽集中绕组永磁电动机还可通过优选槽极配合及优化永磁体形状以抑制齿槽转矩［10-12］。由于槽口分布不均匀，多相分数槽集中整距绕组永磁电动机齿槽转矩频率只含相数整数倍的分量［6］，这一定程度上抑制了齿槽转矩。由于槽极配合数目有限，可进一步研究通过永磁体形状优化抑制齿槽转矩。

优化永磁体形状抑制电动机齿槽转矩时，应遵循既抑制齿槽转矩和转矩脉动，又基本不降低平均转矩的原则。文献［11］通过在五相分数槽集中绕组电动机永磁体上开多个倒梯形小槽的方式抑制齿槽转矩，同时平均转矩为不开小槽时的98%。文献［12］分析了五相分数槽集中绕组电动机在采用径向厚度沿圆周方向呈马鞍形分布永磁体时的转矩性能。马鞍形永磁体由正弦永磁体及第3 次谐波合成得到。该文发现永磁体第3 次谐波分量为基波分量的1/6时得到最大平均转矩，同时齿槽转矩和转矩脉动得到抑制。然而，文献［12］并未进一步分析永磁体形状变化对齿槽转矩的影响。文献［13］指出五相电动机可采用由正弦永磁体及第3，5 次谐波合成得到的准梯形永磁体进一步提高电动机平均转矩，同时齿槽转矩和转矩脉动可得到抑制。为得到最大的平均转矩，文献［13］确定了永磁体谐波分量与永磁体边沿厚度的关系，但也未深入分析永磁体形状对齿槽转矩的影响。

在文献［13］的基础上，本文分析准梯形永磁体边沿厚度对多相分数槽集中整距绕组永磁电动机齿槽转矩的影响。由于永磁体谐波分量的幅值依边沿厚度而定，确定准梯形永磁体形状时只需确定边沿厚度。此外，由于解析法反映电动机尺寸参数与电磁参数的关系，计算速度快，利于电动机初始设计和优化［2］，本文采用解析法计算齿槽转矩并确定齿槽转矩最小时对应的永磁体形状。齿槽转矩解析计算模型主要包括侧向力、复数磁导率、子域和精确子域模型［14］。本文采用的复数磁导率模型概念清晰，建模方便。由于忽略保角变换引起的气隙磁通密度计算路径的畸变，采用该模型得到的齿槽转矩幅值偏大，但这不影响分析电动机参数与齿槽转矩之间的关系，进而指导齿槽转矩的抑制［15］。此外，由于极坐标下准梯形永磁体形状不规则，与空气的边界条件变得复杂，无法采用单一解析式表示电动机无槽气隙磁场，此时可采用微分永磁体法计算无槽气隙磁场［16］。

本文以一台20 槽22 极外转子五相永磁电动机为例，首先对多相分数槽集中整距绕组永磁电动机定子和准梯形永磁体进行说明，其次采用微分永磁体法和复数磁导率模型计算不同准梯形永磁体边沿厚度情况下的电动机齿槽转矩，进而得到最优准梯形永磁体形状。齿槽转矩解析结果得到了有限元结果的验证。最后通过测量采用最优准梯形永磁体样机的齿槽转矩，验证了解析法及其结论的有效性。

1 多相分数槽集中整距绕组电动机

图1所示电动机为采用准梯形永磁体的20 槽22 极外转子五相分数槽集中整距电动机。

图1 20 槽20 极分数槽集中整距绕组永磁电动机Fig.1 The 20-slot 22-pole fractional-slot concentrated full-pitch winding permanent magnet machine

1.1 定子

分数槽集中整距电动机的定子可采用不含小齿和含小齿两种结构［6］，图1所示的含小齿结构可提高电动机的容错性能。如图1所示，定子含10 个定子单元。每个单元中，小齿宽机械弧度为π/(mp)(m 为相数，p 为极对数)。该特征保证了相邻2 个大齿中心线距离θt等于极距，因此绕组系数为1。此外，小槽由小齿将大槽一分为二而得，因此可将2 个连续小槽看成1 个大槽，即认为图1所示定子含20 个槽。

1.2 准梯形永磁体

如图1所示，准梯形永磁体的径向厚度Hv(θ)(θ∈［0，π］为永磁体的空间位置)可分为边沿厚度He和可变厚度两部分。可变部分由正弦及第3，5 次谐波分量合成。Hv(θ)的最大值为Hm，假设

则永磁体径向厚度可表示为

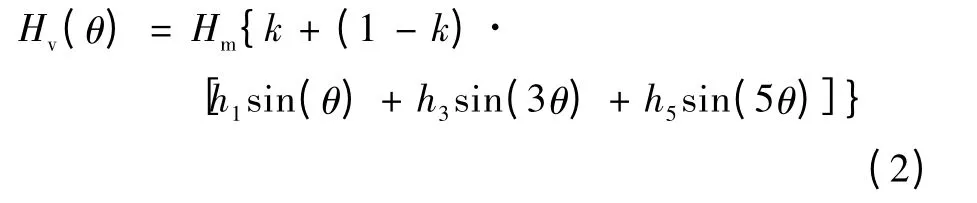
式中h1、h3和h5分别为永磁体径向厚度可变部分基波、第3 次和第5 次谐波的幅值系数。为保证电动机最小有效气隙长度不变，h1、h3和h5满足

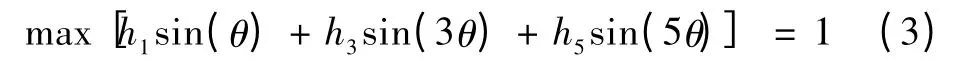
此外，为获得最大平均转矩，h1、h3和h5将随边沿厚度变化而改变［13］。表1 为k 值对应的20 槽22 极外转子五相分数槽集中整距电动机(电动机参数如表2所示)的h1、h3和h5。显然，只要k 值确定，准梯形永磁体的形状就已确定。k=1时，永磁体形状不再是准梯形，而是常规的瓦片状。

表1 与k 值对应的h1、h3和h5Tab.1 h1、h3and h5values corresponding to k

2 最优准梯形永磁体

最优准梯形永磁体的确定原则是采用该永磁体的电动机产生最小齿槽转矩。如前所述，h1、h3和h5的值随k 而定。因此，只要分析电动机齿槽转矩与k 的关系，并得到最小齿槽转矩对应的k，最优准梯形永磁体就能确定。此外，相对于有限元法，采用解析法分析齿槽转矩时无需反复建模、计算速度快。本节采用复数磁导率模型计算不同k 对应的齿槽转矩，进而确定齿槽转矩最小时对应的k 和最优永磁体。复数磁导率模型首先计算电动机无槽气隙磁场，再通过复变量保角变换求得气隙的复数相对气隙磁导函数，然后与电动机无槽时的气隙磁场相乘得到计及定子开槽影响的径向和切向气隙磁通密度，进而采用麦克斯韦张量法计算得到齿槽转矩。

2.1 无槽气隙磁通密度

如前所述，采用准梯形永磁体的电动机气隙不规则，可用微分永磁体法准确计算无槽气隙磁通密度［16］。图2为微分永磁体的结构图，为便于比较，图中只给出半个圆周范围内的气隙磁通密度。图中准梯形永磁体被微分为N 块宽度相同的永磁体，θj为第j块微分永磁体的空间位置。当N 足够大时，可认为第j 块微分永磁体形状规则，且θj为常数。给定电动机尺寸和永磁体磁化方向时，按文献［16］中式(27)～式(54)，先计算单个微分永磁体产生的气隙磁场，再叠加得到单个永磁体产生的气隙磁场，继而得到转子永磁体产生的气隙磁场径向和切向分量。计算气隙磁通密度时第j 块微分永磁体半径可表示为

式中Rr为外转子电动机的转子内径或内转子电动机的转子外径。

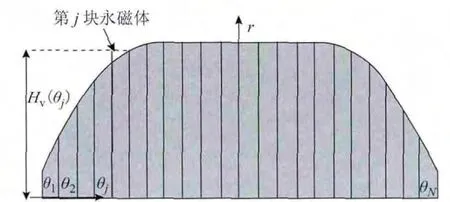
图2 微分永磁体Fig.2 Segmented permanent magnets

图3为k=0 和k=1时20 槽22 极外转子五相分数槽集中整距电动机无槽气隙磁通密度的解析计算结果。可见，相对于k=1时的常规永磁体，准梯形永磁体改变了电动机的气隙磁导，无槽气隙磁通密度径向分量的波形顶部宽度变小且出现纹波，切向分量的峰值减小且出现纹波。无槽气隙磁通密度分布随k 变化而改变，将影响电动机的齿槽转矩，也使通过改变永磁体形状削弱齿槽转矩成为可能。

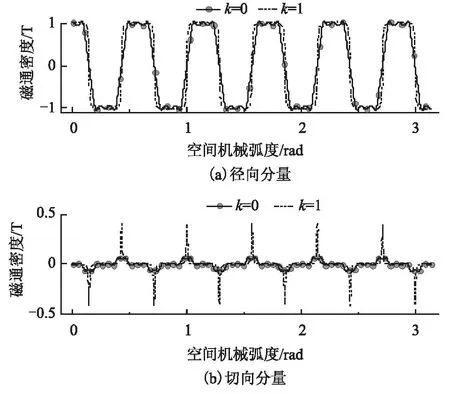
图3 k=0 和k=1时的无槽气隙磁通密度Fig.3 Radical and tangential slotless flux density in cases of k=0 and k=1

2.2 复数相对气隙磁导率

复数相对气隙磁导率可通过复变量保角变换求得［15］。分数槽集中整距电动机复数相对气隙磁导率以定子单元跨距为周期分布，可先计算定子单元内每个齿距的值，再合成得到定子单元跨距的值。此外，对于外转子电动机，z 平面到ω 平面保角变换表达式应由文献［15］中的式(6)修正为

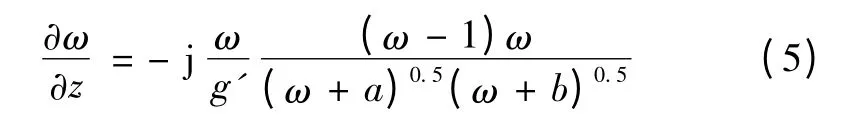
20 槽22 极外转子五相分数槽集中整距电动机气隙中心处复数相对气隙磁导率的实部和虚部如图4所示。由于齿槽分布和槽口大小不均匀，复数相对气隙磁导率的实部与虚部图形都不对称。

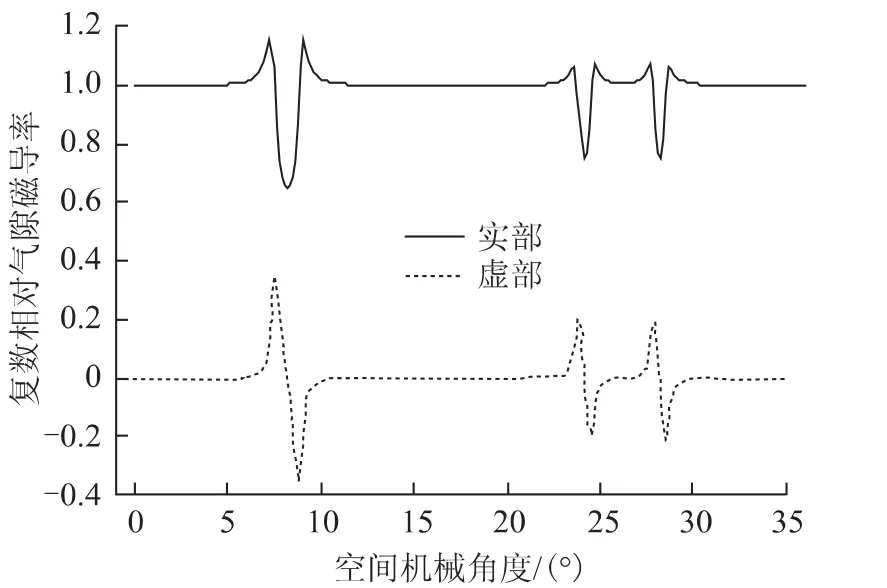
图4 复数相对气隙磁导率的实部与虚部波形Fig.4 Real and imaginary part waveforms of the complex relative air-gap permanence

2.3 齿槽转矩与最优准梯形永磁体的确定

如果已知无槽气隙磁通密度径向和切向分量Bslr和Bslα以及复数相对气隙磁导率实部与虚部λr和λα，则有槽气隙磁通密度径向和切向分量Bsr和Bsα分别为［15］

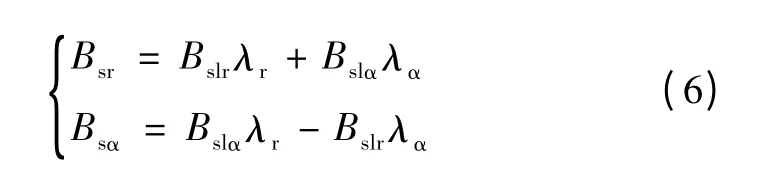
图5为k=0时20 槽22 极外转子五相分数槽集中整距电动机半个圆周范围内有槽气隙磁通密度径向和切向分量的解析和有限元计算结果对比。可见，径向分量误差可忽略，而切向分量在离散区域(虚线框)存在较大误差。引起误差的原因主要是在计算复数相对气隙磁导率时，忽略了槽开口保角变换引起的磁通密度计算路径的畸变，造成有槽气隙磁通密度尤其是切向分量的误差［14，15］。

由麦克斯韦张量法，齿槽转矩可表示为

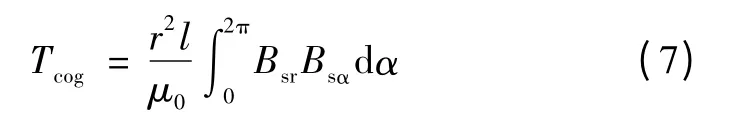
式中:l 为铁心有效长度;r 为计算无槽气隙磁通密度时采用的半径;μ0为真空磁导率;α 为圆周切向位置。

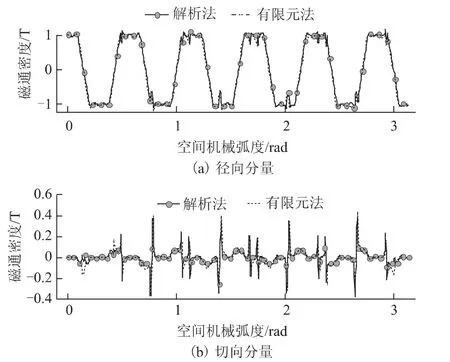
图5 k=0时的开槽气隙磁通密度Fig.5 Radical and tangential slotted flux density in case of k=0

图6为k=0时20 槽22 极外转子五相分数槽集中整距电动机齿槽转矩的解析和有限元计算结果。可见，齿槽转矩波形、频率的解析计算结果与有限元结果吻合，但由于气隙磁通密度计算误差，齿槽转矩峰值比有限元结果大。

图6 k=0时的齿槽转矩Fig.6 Cogging torques of the machine in case of k=0

图7为电动机齿槽转矩峰值与k 关系的解析和有限元结果。由图7a 可见，解析结果在全局范围内均比有限元结果大，且当k 以0.1 的步长从0.4 递增到1时，齿槽转矩幅值的解析值分别对应有限元值的134%、156%、164%、194%、197%、201%和204%。显然，两类齿槽转矩计算结果之间的差值随着k 的增加而增大。这是因为随着k 增加，无槽气隙磁通密度的切向分量增加，磁通密度计算路径畸变造成的有槽气隙磁通密度切向分量误差越大。

然而，复数磁导率解析模型虽不能在全局范围内准确计算齿槽转矩，但揭示了永磁体形状变化对齿槽转矩的影响规律，是永磁体形状优化分析的有效手段。由图7a 可知，k=0.5时电动机具有最小的齿槽转矩。进一步地，图7b 为k=0.45，0.46，…，0.55情况下电动机齿槽转矩峰值的解析结果。可见，k=0.49 和k=0.5时齿槽转矩峰值最小且数值相当。考虑永磁体加工难度，20 槽22 极外转子五相分数槽集中整距电动机应采用k=0.5 的准梯形永磁体。

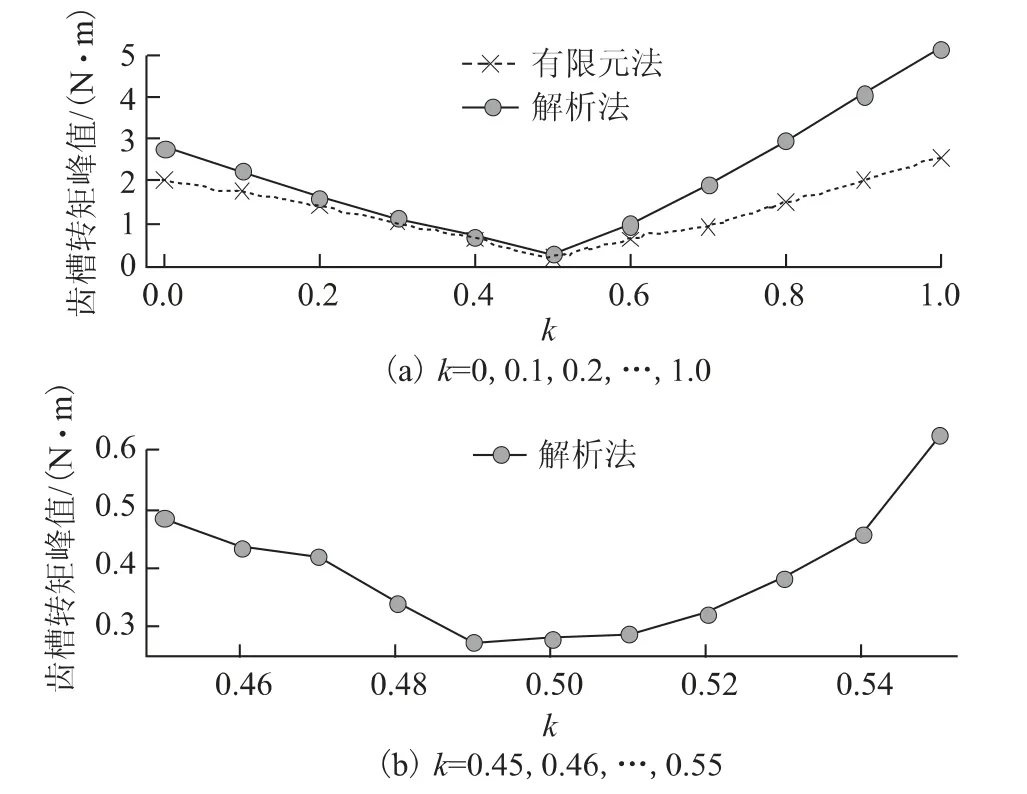
图7 齿槽转矩峰值与k 的关系曲线Fig.7 Variation of peak cogging torque with k

当k=0.5时，电动机齿槽转矩峰峰值的有限元计算结果为0.37 N˙m，为额定转矩的0.41%，对电动机转矩性能影响很小。因此，优化的准梯形永磁体对提升电动机转矩性能有重要作用，该作用在文献［13］中有专门分析，本文不做详述。

对于不同相数和电动机尺寸的表贴式永磁电动机，均可采用上述解析方法进行寻优计算，进而确定最优的永磁体形状。

3 实验验证

图8为采用准梯形永磁体的20 槽22 极外转子五相分数槽集中整距样机转子。样机的主要设计参数如表2 所示。根据解析和有限元优化结果，准梯形永磁体设计为k=0.5。

测量永磁电动机齿槽转矩的方法中，文献［17］提出的电子称法测量结果接近有限元计算值，但对实验设备要求较高，本文采用砝码法进行测量［18］。图9为采用砝码法测量齿槽转矩的测试台架。图中支杆应采用刚度高的材料，且与电动机轴紧密卡合。刻度板最小分度为0.5°，测量角度范围为0°～6.5°，对应2 个齿槽转矩周期。测量时，若齿槽转矩随支杆转角增加而减小，则应将称重袋挂接在支杆的另一端。测得第i 点的砝码转矩Tmi，且认为摩擦转矩Tf为恒定值，则Tf等于所有Tmi的平均值。此时第i 点的齿槽转矩为

图8 电动机转子与永磁体Fig.8 Rotor and the permanent magnets

表2 样机主要设计参数Tab.2 Main design parameters of prototype machine

图9 齿槽转矩测试台架Fig.9 Set-up of cogging torque measurement

测量得到的电动机齿槽转矩如图10所示，图中还给出了k=0.5时电动机齿槽转矩2 个周期的解析和有限元计算结果。为便于比较，实验得到的14 个数据采用虚线连接。由图10可知，相对于有限元结果，实测齿槽转矩峰值更大，大部分数值存在偏差，但具有较好的吻合度。数值偏差的原因是测量时需人工判断正确的砝码重量、测量器材准确度和电动机加工准确度不足。此外，实测齿槽转矩的变化周期与解析和有限元结果一致。

图10 k=0.5时的齿槽转矩Fig.10 Cogging torques of the machine in case of k=0.5

实测齿槽转矩的峰峰值为0.5 N˙m，为额定转矩的0.56%。因此，采用优化的准梯形永磁体可有效抑制电动机齿槽转矩及其负面影响。

4 结论

本文分析了基于准梯形永磁体的多相分数槽集中整距绕组永磁电动机齿槽转矩抑制，研究了准梯形永磁体边沿厚度对齿槽转矩的影响，得到了最小齿槽转矩对应的永磁体边沿厚度和永磁体形状。为提高优化速度，可采用微分永磁体法和复数磁导率模型计算不同边沿厚度时的齿槽转矩，并确定最优准梯形永磁体形状。以一台20 槽22 极外转子五相分数槽集中整距样机为例，解析结果发现采用准梯形永磁体的电动机齿槽转矩比采用普通永磁体(k=1)时更小，且齿槽转矩最小时边沿厚度为最大厚度的0.5 倍。齿槽转矩的解析结果得到了有限元验证。样机实测结果表明，采用最优准梯形永磁体时齿槽转矩及其影响得到有效抑制。准梯形永磁体适用于其他尺寸的多相永磁电动机。此外，复数磁导率模型能揭示永磁体参数对齿槽转矩的影响规律，是调整永磁电动机参数抑制齿槽转矩的有效分析方法。

［1］ Levi E．Multiphase electric machines for variable-speed applications［J］．IEEE Transactions on Industry Electronics，2008，55(55):1893-1909．

［2］ 郭思源，周理兵，齐歌．双三相永磁同步电动机电磁性能解析计算［J］．电工技术学报，2014，29(5):17-28．

Guo Siyuan，Zhou Libing，Qi Ge．Analytical calculation of electromagnetic performance in dual three-phase permanent magnet brushless AC machines［J］．Transactions of China Electrotechnical Society，2014，29(5):17-28．

［3］ EL-Refaie A M．Fractional-slot concentrated windings synchronous permanent magnet machines:opportunities and challenges［J］．IEEE Transaction on Industry Applications，2010，57(1):107-121．

［4］ Leila P，Hamid A T．Five-phase permanent-magnet motor drives［J］．IEEE Transactions on Industry Applications，2005，41(1):30-37．

［5］ Wang Jin，Zhou Libing，Qu Ronghai．Harmonic current effect on torque density of a multiphase permanent magnet machine［C］．International Conference on Electrical Machines and Systems，Beijing，2011:1-6．

［6］ Chen Yiguang，Du Zhiming，Zhong Weigang，et al．Modular stator structure permanent magnet synchronous machine［C］．World Automation Congress，Hawaii，HI，2008:1-5．

［7］ Kang Huilin，Zhou Libing，Wang Jin．Harmonic winding Factors and MMF analysis for five-phase fractional-slot concentrated winding PMSM［C］．International Conference on Electrical Machines and Systems，Busan，2013:1236-1241．

［8］ 黄守道，刘婷，欧阳红林，等．基于槽口偏移的永磁电动机齿槽转矩削弱方法［J］．电工技术学报，2013，28(3):99-106．

Huang Shoudao，Liu Ting，Ouyang Honglin，et al．A method for reducing cogging torque by slot-opening shift in permanent magnet motors［J］．Transactions of China Electrotechnical Society，2013，28(3):99-106．

［9］ 刘婷，欧阳红林，黄守道．基于重复单元削弱永磁风力发电动机齿槽转矩［J］．电工技术学报，2011，26(12):43-48．

Liu Ting，Ouyang Honglin，Huang Shoudao．Reducing cogging torque in permanent magnet wind power generators based on repeat unit［J］．Transactions of China Electrotechnical Society，2011，26(12):43-48．

［10］ EL-Refaie A M，Shah M R，Qu Ronghai，et al．Effect of number of phases on losses in conducting sleeves of surface PM machine rotors equipped with fractional-Slot concentrated windings［J］．IEEE Transactions onIndustry Applications，2008，44(5):1522-1532．

［11］ Scuiller F．Magnet shape optimization to reduce pulsating torque for a 5-phase PM low speed machine［J］．IEEE Transactions on Magnetics，2014，50(4):1-9．

［12］ Wang Kai，Zhu Z Q，Ombach G．Torque improvement of five-phase surface-mounted permanent magnet machine using 3rd order harmonic［J］．IEEE Transactions on Energy Conversion，2014，29(3):735-747．

［13］ Kang Huilin，Zhou Libing，Wang Jin，et al．Magnet shape optimization of five-phase surface-mounted permanent magnet machine to improve torque performance based on equivalent permanent magnet method［J］．IEEJ Transactions on Electrical and Electronic Engineering，2015，10(S1):133-143．

［14］ Wu L J，Zhu Z Q，Staton D，et al．Comparison of analytical models of cogging torque in surface-mounted PM machines［J］．IEEE Transactions on Magnetics，2012，59(6):2414-2425．

［15］ Zarko D，Ben D，Lipo T A，et al．Analytical solution for cogging torque in surface permanent-magnet motors using conformal mapping［J］．IEEE Transactions on Magnetics，2008，44(1):52-65．

［16］ Wu L J，Zhu Z Q．Analytical modeling of surfacemounted PM machines accounting for magnet shaping and varied magnet property Distribution［J］．IEEE Transactions on Magnetics，2012，50(7):8101511．

［17］ Zhu Z Q．A simple method for measuring cogging torque in permanent magnet machines［C］．Power＆Energy Society General Meeting，Calgary，AB，2009:1-4．

［18］ 张宁，罗玲，李丹，等．永磁电动机齿槽转矩的测量［J］．微电动机，2012，45(10):23-26．

Zhang Ning，Luo Ling，Li Dan，et al．Measuring cogging torque in permanent magnet electric machines［J］．Micromotors，2012，45(10):23-26．