基于FSAD及非周期分量的励磁涌流鉴别算法

王 业 袁宇波 高 磊 陆于平 朱 磊

(1.江苏省电力公司电力科学研究院 南京 211103 2.东南大学电气工程学院 南京 210096)

0 引言

变压器差动保护在系统正常运行和区外故障时，理想情况下流入差动继电器的电流为零，保护装置不动作。但实际上当变压器空载合闸产生励磁涌流时，励磁涌流的大小将达到变压器额定电流的几倍甚至十几倍。另一方面，励磁涌流只流过变压器的电源侧，而负荷侧因开路并没有电流，励磁涌流将完全流入纵差保护的差动回路，使差动继电器中产生了一个非常大的不平衡电流［1］。同时，随着变压器容量的不断增大及变压器饱和磁通的逐渐降低(考虑成本因素)，事实证明，如今涌流波形已并非全部严重畸变。变压器在超饱和状态下有可能产生趋于正弦波型的励磁涌流，二次谐波含量很低，间断角很小，使得基于二次谐波制动理论与基于间断角闭锁理论的差动保护无法正常工作。

而在现今的变压器差动保护研究领域，变压器超饱和现象并未被学者们重点关注，大部分学者的研究重点还放在变压器常规饱和引起的涌流方面。根据涌流区别于内部故障电流的特征，学者们提出了许多识别常规涌流的方法［1-6］，主要有二次谐波制动原理、间断角原理、波形对称原理波形时域分布特征原理、广义基波功率原理及磁制动原理等。但由于对超饱和现象的关注还不够深入，这些方法在鉴别变压器超饱和态涌流的效果上并不理想，保护时有误动作发生。因此，研究用于鉴别超饱和情况下励磁涌流的方法对提高变压器保护的性能具有重要的意义。

本文首先对励磁涌流的产生机理进行分析，然后结合其产生机理给出变压器发生超饱和现象及其易使现有差动保护误动的原因，最后提出一种利用基波相位的2 倍与二次谐波相位之差(Fundamental harmonic and Second harmonic Angle Difference，FSAD)及非周期分量来鉴别超饱和态涌流的有效方法，该方法能迅速地鉴别出超饱和态涌流，且能够在变压器内部故障时使得保护具有较快的动作速度。

1 变压器超饱和现象产生机理

1.1 励磁涌流的数学表达式

当变压器空投或区外故障切除电压恢复正常的过程中，由于磁通不能突变，磁通中出现了非周期性的暂态分量，与铁心剩磁一起使变压器铁心饱和，同时由于电压是交变的，因而在一个周波内变压器铁心周期性地进入饱和区和退出饱和区［7-10］。设Φs为饱和磁通，则当瞬时磁通Φ ＞Φs时，变压器进入饱和状态，励磁电流i(t)的瞬时值很大，对应图1中c 区的θ1～θ2段;而当瞬时磁通Φ ＜Φs时，变压器退出饱和区，只有正常的励磁电流，其瞬时值很小，几乎为零，对应图1中c 区的0～θ1和θ2～2π 段，所以涌流在一个周期内存在间断角。

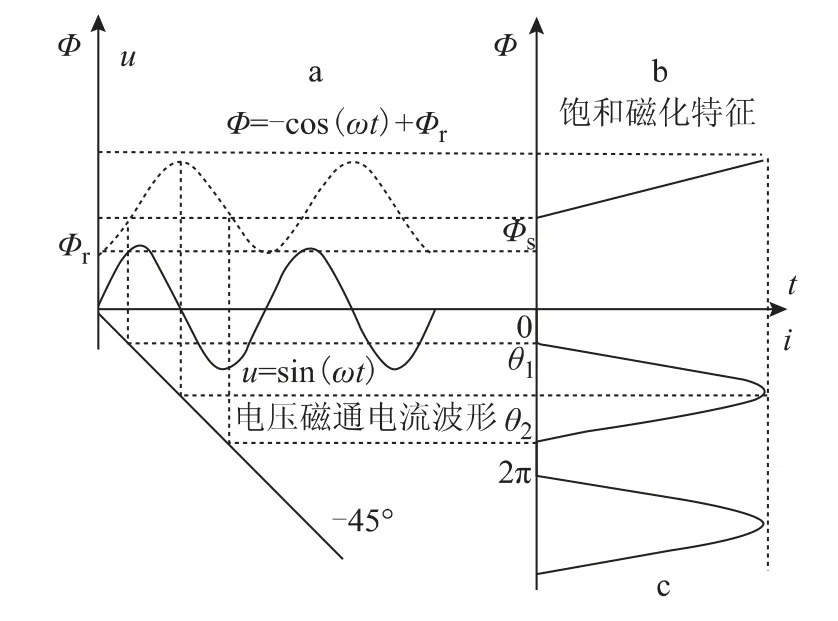
图1 变压器空载合闸时电压磁通电流波形Fig.1 The voltage flux current waveform when the transformer switches on without the load

忽略涌流的衰减，用两段折线表示励磁特性曲线，则励磁涌流的解析表达式为［1］

当Φ ＞Φs时

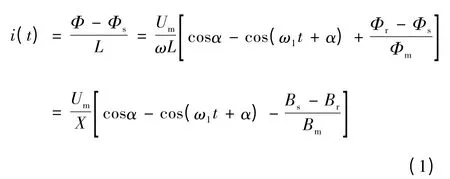
式中:Um为电压幅值;L 为合闸回路电感;α 为合闸角;Φr为剩磁磁通;Φm为磁通幅值;Bs、Br及Bm分别为与Φs、Φr及Φm对应的磁感应强度。

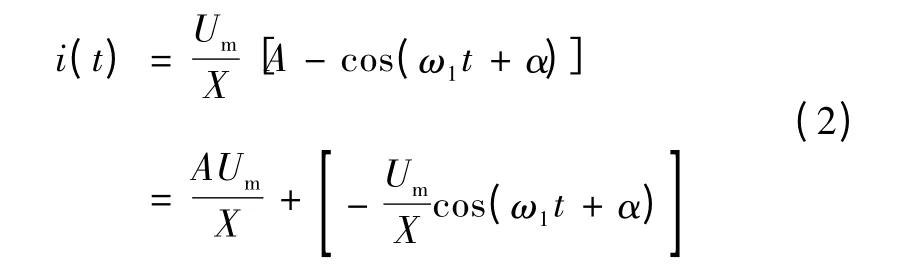
当Φ ＜Φs时，励磁电流i ≈0。

由式(2)可看出，非周期分量id的大小由α 确定，当α=0时，单相变压器满足产生最大涌流的条件，则在合闸后一段时间内，当交流量也达到最大值时，变压器产生最大励磁涌流。

如图1中c 区所示，用θJ表示间断角的大小，则单相变压器励磁涌流的间断角可表示为［1］

1.2 变压器超饱和态涌流产生机理分析

由图1中的a 区所示，当Φr小于Φs时，瞬时磁通必有一部分在Φs以下，其对应的励磁电流约等于零，所以涌流是有间断角的。

但变压器在投运之前，需要进行直流电阻的测量。测量结束后，变压器的剩磁通常会较大。如没有消磁而直接对变压器空载合闸，理论情况下Φr有可能会等于Φs。现将Φr=Φs带入式(4)，可得

则当合闸角α=0时，间断角θJ=0。此时，瞬时磁通将会全部在Φs以上，励磁电流i(t)可表示为

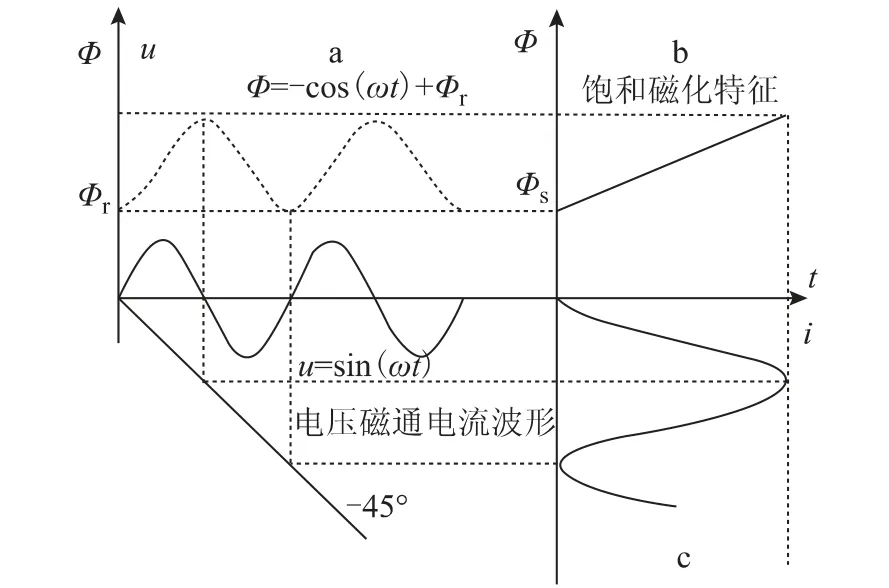
图2 变压器超饱和时电压磁通电流波形Fig.2 The voltage flux current waveform of the ultra-saturated transformer

2 超饱和态涌流鉴别判据的原理及实现

2.1 最大单侧性涌流谐波特征及非周期分量分析

根据第1 节的分析，超饱和态涌流二次谐波含量很低，间断角几乎为零，需要寻找新的方法对其进行鉴别。本节对单侧及对称涌流的相关特征进行分析，用于寻找鉴别超饱和态涌流的新方法。

以Y0/D-11 变压器为例，对于三相涌流而言，涌流峰值的最大值出现在初始电压角α=±30°［11］时。现假设三相初始磁通如图3a 所示，则ia－ib出现最大单侧涌流。图3b 为励磁电流ia和－ ib的波形及两相励磁电流叠加后的波形(此处考虑到波形异侧因素，故在分析ia－ib造成的最大单侧涌流时，将ib反转至时间轴正侧，即用－ib来进行分析)。图3c 为a 相和b 相的基波及二次谐波相位关系，同样由于ia与ib异侧，则要将－ib看成滞后ia60°进行分析计算。做一代表性分析，假设a 相和b 相的基波幅值相等，且二次谐波含量也相等，以a 相电流为基准，分析a 相和b相基波及二次谐波幅值与相位关系。由矢量分析可知，－Ib1滞后Ia160°，而由于二次谐波旋转速度是基波的两倍，故－Ib2滞后Ia2120°。则令φ1=∠(Ia1－Ib1)=－30°，φ2=∠(Ia2－Ib2)=－60°。可得基波与二次谐波相位关系为

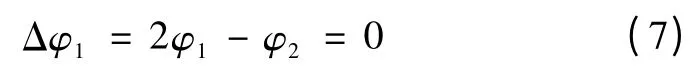
式中Δφ1为单侧涌流时2 倍基波相角与二次谐波相角之差(FSAD)。

图3 最大单侧涌流特性分析Fig.3 The single-side magnetizing inrush characteristic analysis

现对谐波及非周期分量进行定量计算:①对于单相涌流ia或ib，Ia0/Ia1=108.1%、Ia2/Ia1=15.46%;②对于两相叠加后的最大单侧涌流ia－ib，由图3d 可知，二次谐波Ia2－Ib2的幅值等于Ia2与Ib2，而剩磁造成的非周期分量，Ia0－Ib0增大为Ia0或Ib0的两倍。计算得I0/I1=124.9%、I2/I1=8.39%。

对于单侧涌流:①基波相位的2 倍与二次谐波相位之差为0 或180°(单侧负向涌流);②二次谐波含量与非周期分量会呈一定关系，此时非周期分量变大，二次谐波含量变小;③单侧涌流二次谐波含量最小为8.39%，小于我国常用二次谐波闭锁定值15%，所以如果此时使用分相闭锁判据，则空载合闸时保护有可能会误动。

2.2 最大对称性涌流谐波特征及非周期分量分析

假设三相初始磁通如图4a 所示，则可形成对称性涌流，且ia－ib为最大对称性涌流。图4b 为励磁电流ia和ib的波形。图4c 为两相励磁电流叠加后的波形。图4d 为a 相和b 相的基波及二次谐波相位关系，由于此时a、b 两相剩磁相同，故此时可直接将Ia看成超前Ib120°，对两相基波及二次谐波进行分析计算。同样假设a、b 两相的基波幅值相等，且二次谐波含量也相等，以a 相电流为基准，分析a 相和b 相基波及二次谐波幅值与相位关系。由矢量分析可知，Ib1滞后Ia1120°，而由于二次谐波旋转速度是基波的两倍，故Ib2滞后Ia2240°，则φ1=∠(Ia1－ Ib1)=30°，φ2=∠(Ia2－Ib2)=－30°。可得基波与二次谐波相位关系为

式中Δφ2为2 倍基波相角与二次谐波相角之差(FSAD)。

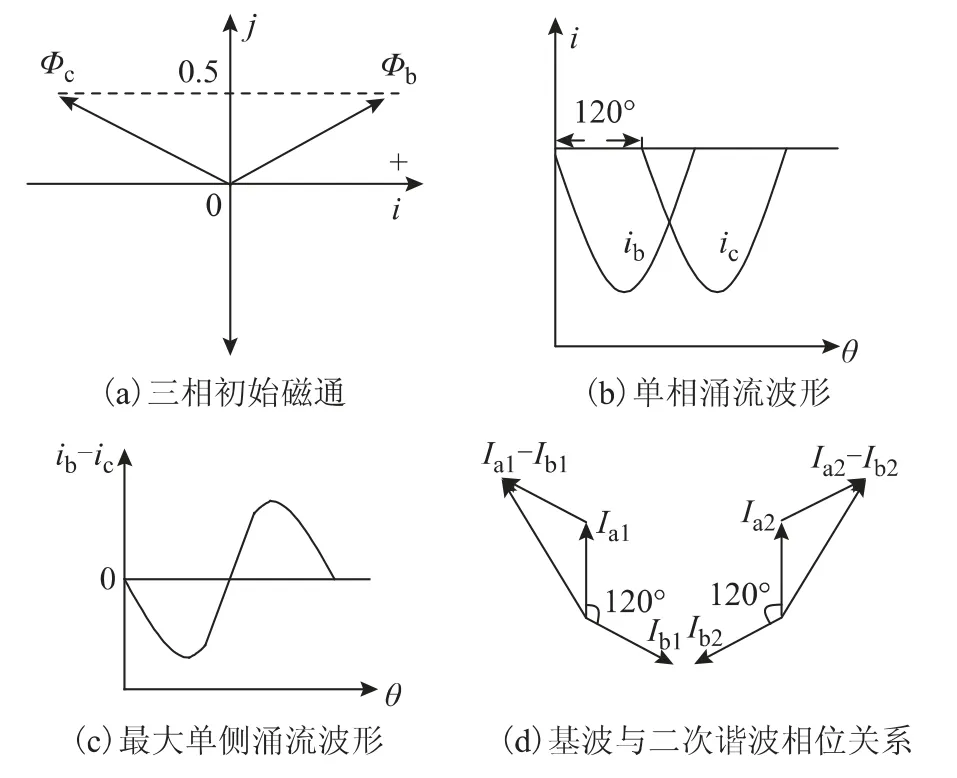
图4 最大对称性涌流特性分析Fig.4 The symmetric magnetizing inrush characteristic analysis

对谐波及非周期分量的比值进行定量计算。对于单相涌流ia或ib，Ia0/Ia1=94.39%、Ia2/Ia1=33.53%。对于两相叠加后的最大对称性涌流ia－ib，由图4d 可知，二次谐波Ia2－Ib2的幅值等于或，而由于A、B 两相剩磁相同，故Ia0－Ib0为0。计算得I0/I1=0、I2/I1=33.53%。

对对称性涌流进行总结，可得出如下结论:①FSAD 为90°或－90°(数据窗推移);②二次谐波含量与非周期分量也呈一定关系，此时非周期分量变小，二次谐波含量变大;③对称涌流的二次谐波含量有可能会较大。

而变压器在超饱和状态下，也将产生类似于对称涌流的正弦波形，所以其FSAD分布满足对称涌流时的FSAD分布规律。

综上所述，可以利用FSAD 及非周期分量两个参数对二次谐波判据进行调节，使保护在变压器发生超饱和时可以可靠制动，而在变压器发生内部故障时，保护能可靠动作。

2.3 保护判据

根据第2.2 节的分析，设保护判据为

式中:k 为经非周期分量调节后的二次谐波含量;I0/I1为非周期分量与基波的比值;I2/I1为二次谐波与基波的比值。判据中设有相位制动区与相位动作区，算法首先通过FSAD 对励磁电流进行分类，再根据分类结果通过非周期分量与基波的比值对励磁电流中包含的二次谐波含量进行调节，并与二次谐波定值进行比较，进而鉴别励磁涌流与故障电流。算法采用分相闭锁机制，当k ＜Kset时算法开放差动保护，当k≥Kset时算法闭锁差动保护。Kset为二次谐波制动比，一般为15%。

需要说明的是，在制定保护判据时，不宜将上述两个参数分开，即不宜单独使用非周期分量或FSAD构成判据，因为:一是如果只使用非周期分量对二次谐波进行调节，再将调节后的二次谐波含量直接与15%的定值进行比较来判断是否发生了涌流，即略去FSAD 参数，这样:ⓐ易造成空投于小匝比故障时保护长时间不开放。因为空投于小匝比故障时，励磁电流波形以涌流特征为主，故障特征为辅，具有较大的二次谐波含量，所以如果不加入FSAD 特征，很难鉴别出此时的故障;ⓑ易造成发生内部故障时保护误闭锁。因为如果故障时差流的非周期分量很大，则根据式(9)调整过的二次谐波含量将会被提高很多倍，如果大于了15%，则保护将会被误闭锁。二是如果只使用FSAD 来进行涌流鉴别，易造成故障时保护延时动作。因为故障时FSAD 是波动的，分布于－ 180°～180°，如果故障发生时刻FSAD 正好处于相位制动区，则保护将延时动作。以上原因将在第3 节仿真过程中进行详细说明。

3 动模实验及实际运行数据实验

3.1 动模接线

在实验室的三单相变压器组上进行动模实验，分析保护算法的动作特性，其系统接线如图5所示，变压器接线为Y0/D-11;额定容量为10 kV˙A，低压侧额定电压为400 V，低压侧额定电流为25 A，高压侧额定电压，高压侧额定电流为17.3 A，空载电流为1.635%。变压器两侧电流互感器二次都采用星形接法，采样率为2 kHz，采用三角侧向星型侧的相位补偿方式。对变压器正常空载合闸、空载合闸时产生超饱和现象、运行中内部接地故障等情况进行实验，每种运行工况分别取100 组数据，选其中较为典型的数据进行分析。根据动模参数，经大量仿真实验，设判 据 式 中 参 数θ1=30°、θ2=32°、K1=3、K2=0.25。

图5 动模系统接线图Fig.5 Connection scheme of the dynamic system

3.2 变压器正常空载合闸(单侧涌流及对称涌流)

图6a 为变压器正常空载合闸情况下三相差流。由图6a 可见，在0.02 s时空载合闸变压器，三相差流中iA和iC为单侧涌流，有明显间断角，且间断角较大，iB为对称涌流，间断角较小。

图6b 是未经本文算法修正前的三相二次谐波含量，由于准确计算二次谐波需一个周期的数据窗，故只考察0.04 s 后的二次谐波含量及各相FSAD 参数Δφ，* 线表示二次谐波整定值，为15%。由图6b 可见，常规涌流二次谐波含量均在15%以上。图6c 中φA、φB、φC分别代表A、B、C 三相FSAD。由前文分析可知，由于A 相差流为单侧正向涌流，其FSAD 应分布于0 或180°左右，B 相为对称涌流，其FSAD 应分布于±90°左右，C 相为单侧负向涌流，其FSAD 应分布于0 或－180°左右，如图6c 所示，该仿真结果与前文分析结果一致。图6d 是经过本文算法修正后的三相二次谐波含量，在正常空载合闸情况下，修正前与修正后的二次谐波含量均在定值15%以上。保护可以可靠制动。

图6 正常空载合闸三相差流、FSAD 及二次谐波含量Fig.6 Three phase differential current，FSAD and second harmonic component when the transformer switches on without the load regularly

3.3 变压器空载合闸时产生超饱和涌流

图7a 为变压器空载合闸时产生的超饱和态涌流波形，由图7a 可见，A、C 两相为单侧涌流，存在很大的非周期分量，其间断角明显减小，几乎不存在。B 相为对称涌流，间断角也大大减小。

由图7b 可见，由于A、C 相发生了超饱和，故两相二次谐波含量均小于15%，且C 相只有8%左右。传统二次谐波制动方法此时无法闭锁差动保护。同时由图7c 可见，由于变压器发生了超饱和，其FSAD分布满足对称涌流时的FSAD分布规律，即分布于90°或－90°附近。B 相对称涌流的FSAD 参数φB依然满足对称涌流FSAD 的分布规律，即分布于90°或－90°附近，故本算法完全有能力鉴别出超饱和涌流。所以由图7d 可见，经本文算法修正后的三相二次谐波含量均大于定值15%，差动保护可靠闭锁。

图7 变压器空载合闸时产生超饱和涌流三相差流、FSAD 及二次谐波含量Fig.7 Three phase differential current，FSAD and second harmonic component when the transformer switches on without the load and generates ultra-saturation phenomenon

3.4 空载合闸于变压器轻微匝间短路故障

图8a 为空载合闸于变压器星形侧A 相1.7%匝间短路故障时的三相差流。由于A 相发生小匝比短路故障，故障电流与涌流同时存在，且故障电流较轻微，所以差流在整体上主要表现为涌流形态，即二次谐波含量较高。如图8b 所示，由于三相差流的二次谐波含量均大于15%，所以此时传统二次谐波制动理论将会闭锁差动保护，直到三相差流的A(ia－ ib)相或C(ic－ia)相二次谐波含量衰减至15%以下时(本次实验中该时刻约为合闸后460 ms)，算法才会开放差动保护。

由图8c 可见，由于星形侧A 相发生了匝间短路故障，故三相差流中A 相FSAD 约为48°和－125°，C 相FSAD 约为40°，不再分布于0°、±90°或±180°左右，偏移出相位制动区。所以根据式(9)，本文算法会对A 相和C 相二次谐波含量进行调节，使其在0.04 s时就已经低于15%，保护无延时动作，如图8d 所示。三相差流中的B(ib－ic)相由于不受故障相的影响，故其FSAD分布仍然遵循涌流FSAD分布规律，即单侧正向涌流FSAD分布在0°或180°附近，如图8c 所示。

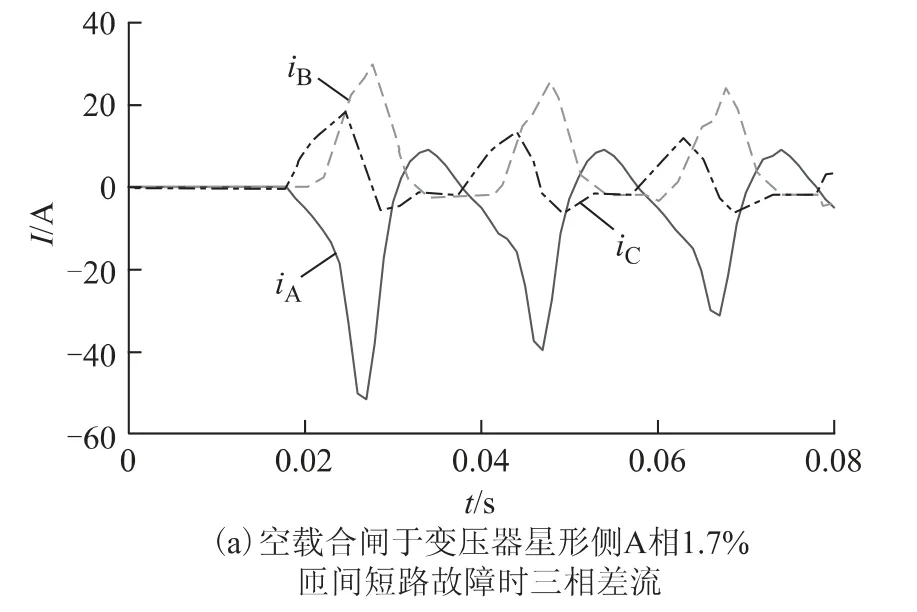
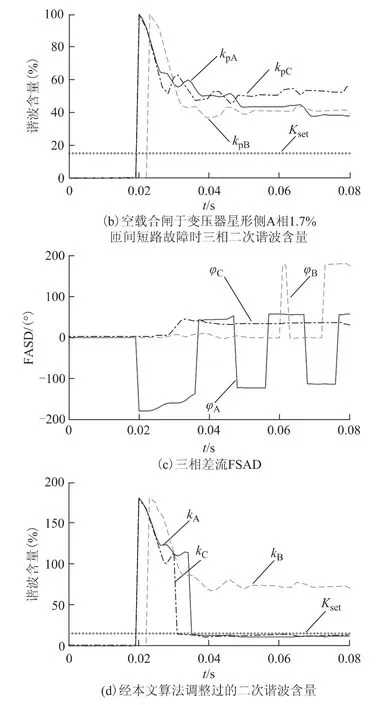
图8 空载合闸于变压器星形侧A 相1.7%匝间短路故障时三相差流、FSAD 及二次谐波含量Fig.8 Three phase differential current，FSAD and second harmonic component when switching on the unloaded transformer with 1.7% turns short circuited

现针对第2.3 节提出的算法为何不单用非周期分量对二次谐波含量进行调节作为鉴别涌流的判据做一详细说明，这里只讨论原因一ⓐ，原因一ⓑ见3.5 节。分析式(9)可知，其中的非周期分量起着对二次谐波含量进行助增的作用，所以当空载合闸于变压器小匝比故障时，差流原先的二次谐波含量就已经超过了15%的定值，此时助增只会进一步加大二次谐波含量，保护将会闭锁。只有通过FSAD 这个因素进行调节，才能在空载合闸于变压器小匝比故障时，使得保护无延时开放。

3.5 运行中变压器内部接地故障

图9a 为运行中变压器星形侧A 相内部接地故障三相差流，由于A 相发生接地故障，故A、C 两相差流增大，B 相差流很小。同时由于发生的是接地故障，故三相差流的二次谐波含量很低，小于15%的定值，如图9b 所示。图9c 为单相接地故障时三相差流FSAD分布示意图，由图9c 可见，单相接地故障时各相差流FSAD 会在0°和±180°之间浮动，即FSAD 会交替分布于相位动作区和相位制动区，所以差动保护必然可靠动作。如图9d 所示，经本文算法调整后的三相差流的二次谐波含量远小于定值15%，所以保护可以可靠动作。

现针对第2.3 节提出的本文判据中不宜只使用非周期分量这个参数对励磁涌流进行鉴别的原因一ⓑ做详细说明:如只使用非周期分量作为式(9)的判据参数(忽略利用FSAD 进行分类)，在变压器发生内部故障且非周期分量很大的情况下，二次谐波含量将会被助增至定值之上，使得保护闭锁。但如果加入FSAD 这个参数，则可提高保护的可靠性。如图9c 所示，故障时差流FSAD 会交替分布于相位动作区和相位制动区，所以就算此时差流的非周期分量很大，FSAD 也将会落入相位动作区，二次谐波含量经调整变的很低，使得保护动作。所以判据中需要加入FSAD 这个参数，提高保护的可靠性。

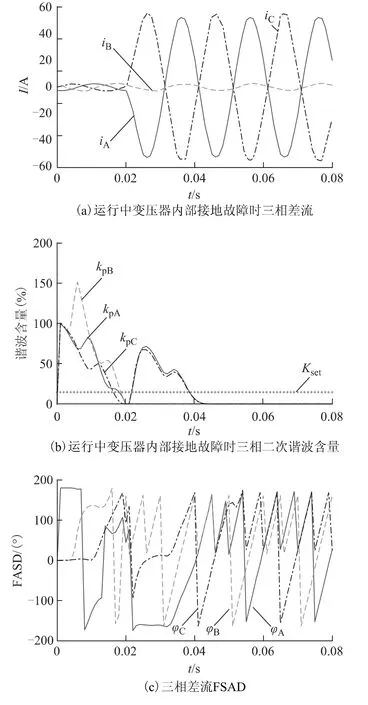
图9 运行中变压器内部接地故障三相差流、FSAD 及二次谐波含量Fig.9 Three phase differential current，angle difference and second harmonic component when the internal single phase to earth fault of transformer occurs during operation

同样，算法也不宜单用FSAD 作为鉴别涌流的惟一判据(第2.3 节原因二):假设只使用FSAD 作为鉴别涌流的判据，即假设判据为如果发现FSAD 落入相位制动区，就闭锁差动保护;如果发现FSAD 落入相位动作区，就开放差动保护。现对上述假设进行分析，如图9c 所示，在0.04s时(故障发生后一个周期)，单相接地故障的三相FSAD 均分布于0°附近，即落入了相位制动区，保护闭锁，只有等到FSAD 逐渐移至相位动作区，保护才能动作。所以如果只使用FSAD 作为鉴别涌流的惟一判据的话，将有可能导致保护延时动作。相反，如果只将FSAD 参数用作对励磁电流进行分类，而在判据中加入非周期分量对二次谐波进行调节，最终通过判断二次谐波含量是否超过定值来决定保护是否动作，则可以提高保护的速动性。

4 结论

为了鉴别出变压器在超饱和状态下的励磁涌流及使得在变压器带轻微故障合闸时不闭锁差动保护，本文提出基于FSAD 及非周期分量的励磁涌流鉴别算法。首先通过FSAD 对励磁电流进行分类，再根据分类结果通过非周期分量与基波的比值对励磁电流中包含的二次谐波含量进行调节，并与二次谐波定值进行比较，进而鉴别励磁涌流与故障电流。该方法主要创新点包括:

1)可以鉴别出二次谐波含量很低的超饱和态涌流，防止保护误动。

2)可以在空载合闸于变压器小匝比故障时不闭锁差动保护，具有较高的灵敏性，而常规二次谐波制动原理在此种情况下将会闭锁差动保护后，且需要等到合闸后460 ms 左右才开放差动保护。

3)加入FSAD 参数，弥补只用非周期分量作为涌流判据的不足之处。如果只用非周期分量作为涌流判据，较难鉴别出空载合闸于小匝比故障。且加入FSAD 参数，可以提高保护的可靠性。

4)通过调整过的二次谐波含量与谐波定值比较，判断保护是否动作，可以在故障时提高保护的速动性。

5)采用分相闭锁，闭锁可靠性较高。

动模实验验证了该方法的有效性及优越性，在变压器发生超饱和、二次谐波含量低于8%时，算法依然可靠闭锁差动保护;同时在变压器星形侧带1.7%匝间短路故障空载合闸时，算法没有闭锁差动保护，且在变压器发生内部单相接地故障时，保护于故障发生后20 ms时可靠动作，速动性较强。

［1］ 王维俭，侯炳蕴．大型机组继电保护理论基础［M］．北京:水利电力出版社，1989．

［2］ 王雪，王增平．基于波形时域分布特征的变压器励磁涌流识别［J］．电工技术学报，2012，27(1):148-154．

Wang Xue，Wang Zengping．Identification of transformer inrush currents based on waveform distribution characteristics［J］．Transactions of China Electrotechnical Society，2012，27(1):148-154．

［3］ 袁宇波，李鹏，黄浩声．变压器差动保护误动原因分析及对策综述［J］．江苏电机工程，2013，32(6):8-11，14．

Yuan Yubo，Li Peng，Huang Haosheng．Review on analysis and strategy for transformer differential protection malfunction［J］．Jiangsu Electrical Engineering，2013，32(6):8-11，14．

［4］ 王雪，王增平．基于广义基波功率的新型变压器主保护方案［J］．电工技术学报，2012，27(12):191-198．

Wang Xue，Wang Zengping．Novel transformer main protection scheme based on generalized fundamental power［J］．Transactions of China Electrotechnical Society，2012，27(12):191-198．

［5］ 张晓宇，文继锋，程晓，等．换流变压器励磁涌流特性及其对差动保护的影响［J］．江苏电机工程，2013，32(5):52-54，58．

Zhang Xiaoyu，Wen Jifeng，Cheng Xiao，et al．The characteristic of the inrush current of converter transformer and its impacts on differential protection［J］．Jiangsu Electrical Engineering，2013，32(5):52-54，58．

［6］ 索南加乐，许立强，焦在滨，等．基于磁路特征的三相三柱式变压器励磁参数识别［J］．中国电机工程学报，2011，31(19):97-104．

Suonan Jiale，Xu Liqiang，Jiao Zaibin，et al．Identification method for excitation inductances of threephase three-limb transformer based on characteristics of magnetic circuit［J］．Proceedings of the CSEE，2011，31(19):97-104．

［7］ 王业，陆于平，蔡超，等．采用自适应数据窗电流的励磁涌流鉴别方法［J］．中国电机工程学报，2014，34(4):702-711．

Wang Ye，Lu Yuping，Cai Chao，et al．A magnetizing inrush identification method applying adaptive datawindow currents［J］．Proceedings of the CSEE，2014，34(4):702-711．

［8］ 王增平，王雪．基于改进主成分分析的变压器励磁涌流识别方法［J］．电力系统保护与控制，2011，39(22):1-5．

Wang Zengping，Wang Xue．Inrush current recognition in power transformer based on modified principal component analysis［J］．Power System Protection and Control，2011，39(22):1-5．

［9］ 熊小伏，齐晓光，欧阳金鑫．双馈风电机组短路电流对变压器保护二次谐波制动的影响［J］．中国电机工程学报，2014，34(13):2201-2209．

Xiong Xiaofu，Qi Xiaoguang，Ouyang Jinxin．Effect of doubly-fed wind turbines short-circuit current on second harmonic escapement of transformer Protection［J］．Proceedings of the CSEE，2014，34(13):2201-2209．

［10］ 邓祥力，高亮，刘建峰，等．特高压变压器模型漏感参数的稳态识别方法［J］．电工技术学报，2014，29(5):255-260．

Deng Xiangli，Gao Liang，Liu Jianfeng，et al．Steadystate parameter identification of UHV transformer model［J］．Transactions of China Electrotechnical Society，2014，29(5):255-260．

［11］ 张保会，尹项根．电力系统继电保护［M］．北京:中国电力出版社，2005．