基于波动传递函数的电网扰动传播频率特性分析

燕跃豪 鲍 薇 李晓方 林 慧

(国网河南省电力公司郑州供电公司 郑州 450006)

0 引言

我国电网已成为超大机组、特高压及交直流互联电网，这在带来规模化效益及互为备用等优势的同时，也使得系统更易因局部扰动蔓延而造成严重后果［1］。近年来，世界各地频繁发生的大停电事故也证实了这一点。事实上，电网扰动难以避免，如果能明晰扰动在系统中的传播规律，并及时采取针对性的控制措施，就能有效降低扰动影响，保障大电网安全［2，3］。因此，研究揭示扰动传播规律具有重要的理论和现实意义。

随着互联电网规模的扩大，扰动在电网中呈现出以近似机械波形式传播的特点，世界多地都观测到了这种现象［4，5］。J.S.Thorp［6］教授将其定义为机电波(Electromechanical Wave)，并尝试引入波动力学理论，从空间和时间角度刻画大电网中的扰动传播规律，这为研究电网扰动传播机理提供了新的思路［7，8］。

采用机电波理论，研究扰动在一维链式电网中的传播规律是研究实际电网扰动传播机理的基础。目前，研究主要从连续体模型［9-11］和离散惯量模型［12，13］两个角度展开。连续体模型假设发电机间距无穷小，将电网处理为发电机惯量及线路电抗连续分布的扰动传播介质。然而实际电网中发电机间距难以忽略;而且仅在发电机处产生扰动反射的现象也与连续体模型的特征不符［14］。与连续体模型相比，离散惯量模型更加符合电网中发电机空间离散分布的特性，但离散惯量系统的研究方法一直是相关物理问题的难点［15，16］。

本文重点研究不同频率的扰动在一维链式电网中的传播特性。借鉴连续体模型中偏微分形式机电波方程的推导思路，在建立基于离散惯量模型的机电波传播方程的基础上，提出波动传递函数的概念，定量刻画机电波波幅、相位在离散惯量模型中的变化规律;进一步通过分析不同频率扰动信号的传播特性，提出了扰动传播转折频率的概念，定量分析了扰动传播过程中的频散效应和局部振荡现象与转折频率的关系。

1 电网离散惯量模型的扰动传播方程及波动传递函数

1.1 电网离散惯量模型的扰动传播方程

以图1所示一维链式电网为例，研究不同频率扰动的传播规律。假定所研究的电网中，忽略发电机的内阻抗，即认为发电机内电动势的相角与所连母线电压的相角一致;同时也忽略线路电阻和发电机阻尼，即认为电网是无损系统。

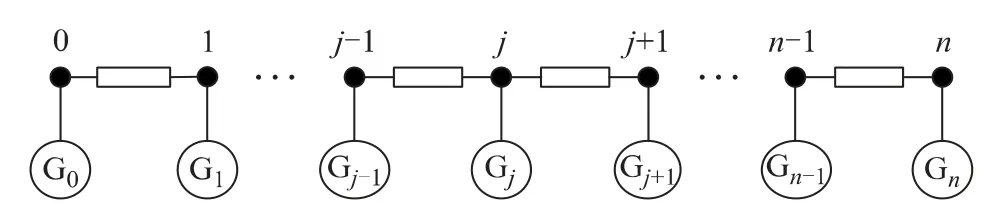
图1 链式电网的离散惯量模型Fig.1 The discrete inertia model of chained power systems

将链式电网在稳态运行点附近进行线性化处理，发电机采用忽略阻尼的二阶经典模型，负荷采用忽略动态过程的恒功率模型，则得到仅由发电机及相连线路构成的电网机电暂态增量系统。图1中发电机Gj的增量转子运动方程为

式中:Δδj为发电机Gj的转子角在稳态值附近的增量;Jj为其转动惯量;ΔPj，j－1、ΔPj，j+1分别为由发电机Gj传输至发电机Gj－1和Gj+1的电磁功率增量。假设整个系统各线路单位长度电抗z 均相等，以发电机G0位置为x 轴坐标原点，发电机Gj和Gj－1、Gj+1线路长度分别为Δxj，j－1和Δxj，j+1。由有功功率传输方程可得

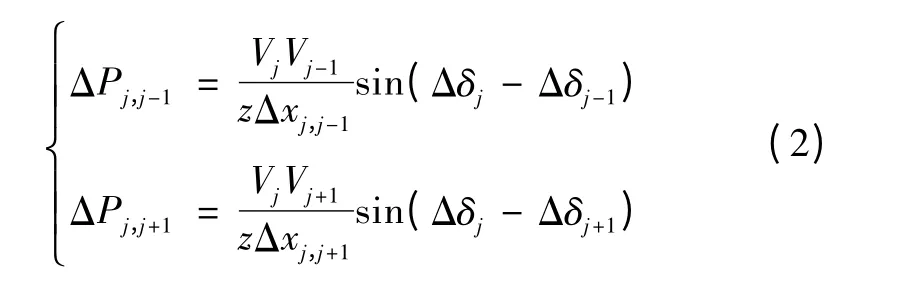
互联大电网中电压等级较高，发电机间电气距离较小。因此有sin(Δδj－Δδj－1)≈Δδj－Δδj－1及sin(Δδj－Δδj+1)≈Δδj－ Δδj+1成立，将式(2)带入式(1)中，可得

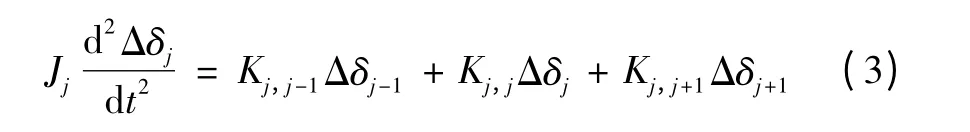
式中K 为发电机间传递的功率。

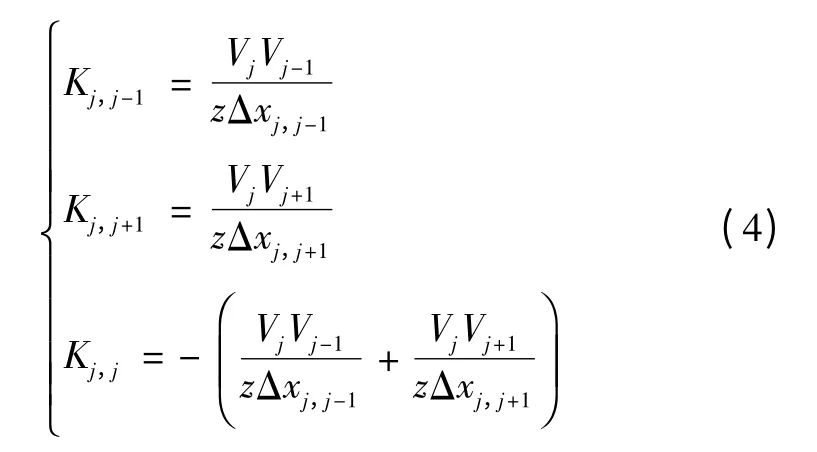
为了便于阐明波动传播问题的本质，假设该链式电网是完全均匀的，即各发电机的转动惯量J 相同，各段线路电压等级V 相等，线路参数及长度Δx 相等。则式(3)可化简为

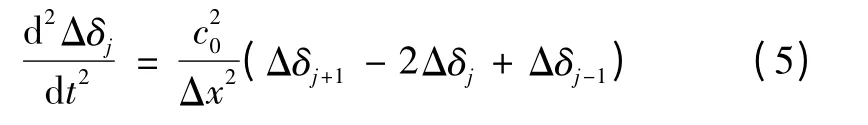
式中:j=0，1，…，n;c0为扰动在对应的连续体均匀链式电网中的传播速度，由以上推导可知

1.2 电网离散惯量模型的波动传递函数

当发电机G0上施加正弦型有功功率扰动ΔP=P0eiωt时，设其在发电机G0上的转子角增量为Δδ0=A0eiωt(其中A0为发电机G0转子角增量的幅值，ω 为其变化频率)，链式系统中其他发电机将产生同频率变化的转子角增量，但其幅值及相位各异。设发电机G0上的扰动在发电机Gj上产生的转子角增量为Δδj=Ajeiωt，其中Aj表示发电机Gj转子角增量的幅值。将Δδj－1、Δδj、Δδj+1以及式(6)代入式(5)，可得

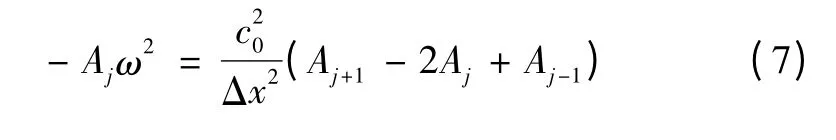
整理式(7)可得

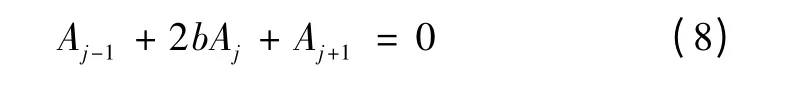
其中

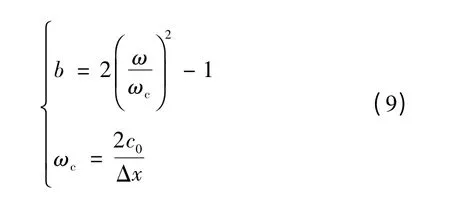
为研究链式系统扰动传播过程中各发电机转子角增量的幅值和相位的变化规律，本文引入波动传递函数γ。对发电机Gj来说，其相关波动传递函数可定义为

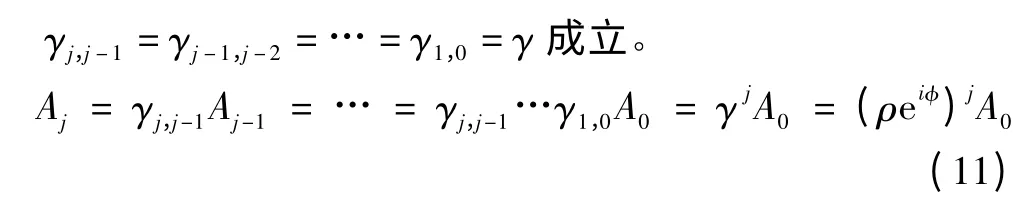
式中ρ、φ分别为波动传递函数γ 的幅值谱和相位谱。

将式(11)代入式(8)，可知ρ 和φ 并非常数，其值主要受发电机G0产生的转子角增量波Δδ0的频率ω影响。当扰动源频率ω 小于ωc时(即ω/ωc＜1)，求解式(8)可得

式中取0≤arcsin(ω/ωc)≤π/2。而当扰动源频率ω 大于等于ωc时(即ω/ωc≥1)，可得

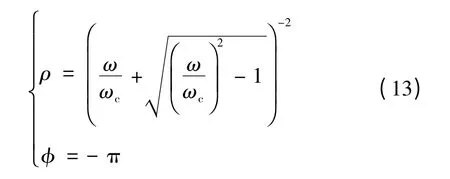
式(11)～式(13)给出了一维均匀电网离散惯量模型中波动传递函数的解。其中，发电机转子角增量的波动传递函数γ 的幅值谱ρ 和相位谱φ 如图2所示。

由图2可知，在一维链式电网中当扰动信号频率ω 小于ωc时，幅值不发生衰减。而当ω ＞ωc时，扰动沿传播方向的幅值会迅速衰减，且相邻节点上的相位角相差达到180°。当ω ＞3ωc时，扰动波的幅值几乎衰减为零。

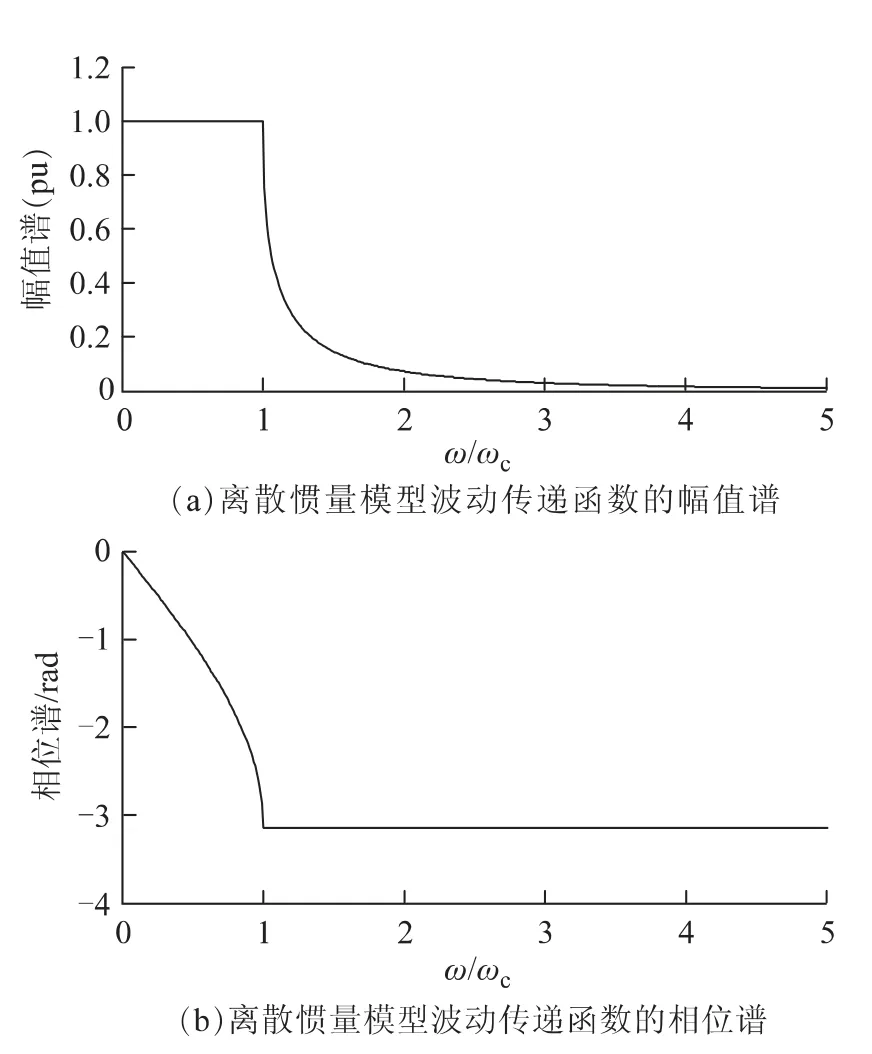
图2 离散惯量模型波动传递函数的幅值谱和相位谱Fig.2 The amplitude and phase spectrum of wave transfer function for discrete inertia model

在此，定义ωc=2c0/Δx 为电网离散惯量模型中扰动传播的转折频率。由以上分析可知，转折频率ωc是电网中扰动传播过程中幅值变化的重要指标，且其完全由系统结构及参数决定。只有低于转折频率的扰动信号才能在电网中继续传播，大于转折频率的扰动信号在传播过程中将迅速衰减。均匀离散惯量系统中的转折频率为固定值，仿真结果证明对于更具普遍性的网格状电网其同样存在扰动传播的转折频率，然而对应的转折频率并不是固定值而是空间位置的函数，非均匀系统可以视为大量局部均匀系统的组合体，即其转折频率可以写为ωc(x，y)=2c0(x，y)/Δx(x，y)。

2 电网离散惯量模型中的频散效应

频散效应是某些波动介质的固有特性，它使得不同频率的扰动信号在介质中以不同速度传播。因此，当扰动信号包含多个频率分量时，扰动波形将在传播过程中产生畸变。离散效应的研究有助于揭示扰动传播过程中的波形变化规律。

以下将分析一维链式电网离散惯量模型中的频散关系，即扰动信号频率与传播速度的函数关系。设沿x 轴正向传播的转子角增量波为

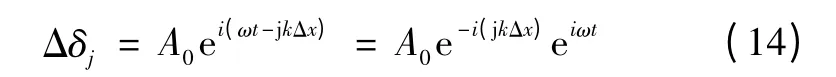
当转子角增量入射波频率ω 小于其转折频率ωc时，由式(11)和式(12)得

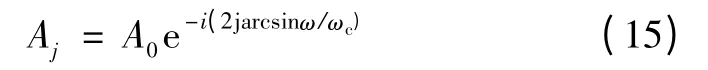
对比式(14)与式(15)，可得

式中k 为扰动入射波的波数。式(16)可写成

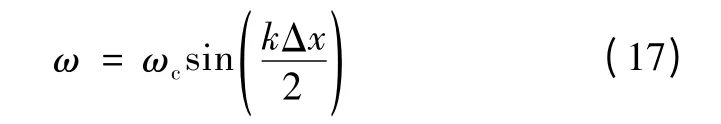
依据波动学原理，电网离散惯量模型中转子角增量入射波传播的相速度cp和群速度cg可定义为

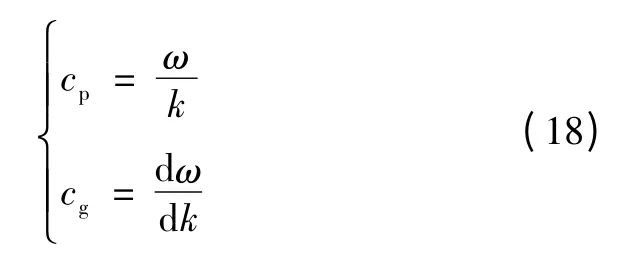
将式(17)带入式(18)得

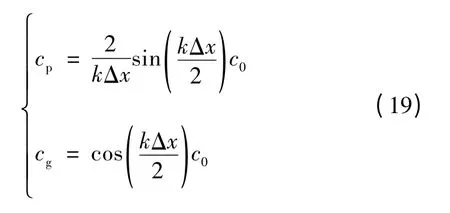
将式(16)带入式(19)，可得用转子角增量入射波频率ω 表示的电网离散惯量模型频散关系为

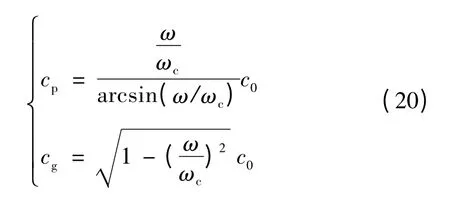
相速度cp和群速度cg与入射波频率ω 的关系如图3所示。

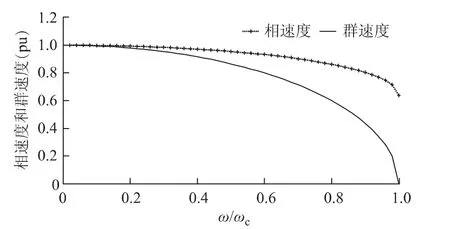
图3 离散惯量模型中的相、群速度与扰动波频率的关系Fig.3 The correlation between phase speed，group speed and frequency of incident wave in discrete inertia model

由图3可知，在一维链式电网中当扰动信号频率小于0.2 倍转折频率时，离散惯量模型中的相速度与群速度基本一致，即该频段内扰动信号的传播速度相等。扰动传播过程中波形几乎不变，频散效应并不明显。随着扰动信号频率的增加，相速度与群速度的偏差逐渐增大。当ω=ωc时，群速度cg=0。即当入射波频率ω 达到转折频率ωc时，扰动能量几乎不能在电网离散惯量模型中传播。

对于网格型均匀电网，上述结论依然成立;对于网格型非均匀电网，由1.2 节结论可知，其转折频率是空间位置的函数，对应的频散分界点0.2ωc也是空间位置的函数。由于不同位置的频散分界点不同，频散现象在非均匀电网中难以直接观察。

3 电网离散惯量模型中的局部振荡

在电网均匀连续体介质模型中，无论扰动信号频率的高低，都将在电网各处产生同频率、同振幅的响应。然而，对于电网离散惯量模型来说，当扰动信号频率ω大于转折频率ωc时，按照式(11)和式(13)可推导得

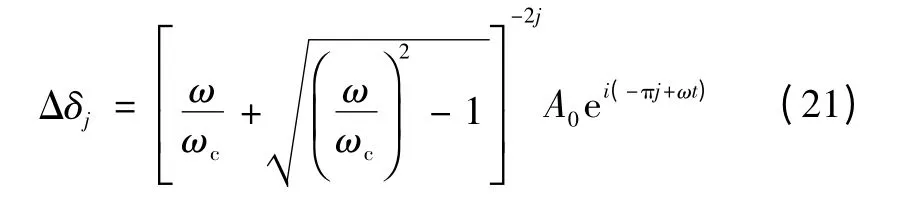
由式(21)可知，电网离散惯量模型中各发电机转子角增量的幅值并非恒定，而是关于扰动信号频率ω和发电机位置j 的函数。图4为发电机转子角增量幅值比Aj/A0分别随扰动信号频率ω 和发电机位置j 的变化曲线。

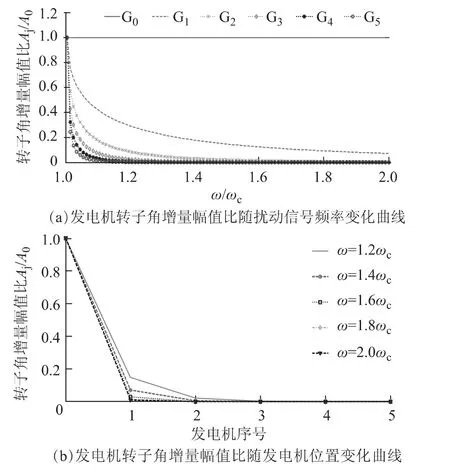
图4 发电机转子角增量幅值比随扰动信号频率及发电机位置的变化曲线Fig.4 The amplitude of rotor angle increments with respect to disturbance frequencies and generator locations

由图4可知，在一维链式电网中当扰动信号频率大于转折频率时，各发电机转子角增量幅值均随扰动信号频率增加而衰减，且距离扰动源越远的发电机的衰减程度越大。在此，定义这种扰动信号幅值在传播过程中随扰动信号频率和发电机位置增加而迅速衰减的现象为离散惯量模型中的局部振荡。

局部振荡是离散惯量模型的特有现象，可以认为发电机具有对高频扰动信号的“滤波作用”。当发生局部振荡时，高频扰动信号将不能在电网中大范围传播。距离扰动源较远的发电机只能观测到较低频率的振荡成分，且振幅远小于扰动源附近发电机的振幅。

通过以上分析可以得出，扰动在一维链式电网中传播的幅值变化规律不仅受与扰动点的距离影响，而且还与扰动频率强相关。根据扰动源的不同频率，扰动传播过程中将发生不同的现象，扰动传播过程中幅值变化规律也截然不同。转折频率ωc和0.2ωc是扰动传播现象的分界点，可将电网离散惯量模型中的扰动按其频率ω 与转折频率ωc的比例关系分为三类(见表1)。

表1 扰动入射波频率与频散和局部振荡的关系Tab.1 The correlation between frequency dispersion，local oscillation and the frequency of incident waves

4 算例分析

在PSD-BPA 仿真软件中建立如图1所示的50 机链式电网，参数取实际电网中常见设备的典型参数。设发电机转动惯量均为20 264 kg˙m2，线路电压220 kV，单位长度电抗0.4 Ω/km，发电机间距100 km。稳态时有10 MW 有功从G0输送到G49。经计算，该链式系统的转折频率ωc为27.57 Hz。在发电机G0上施加不同频率的不平衡有功扰动，以验证电网离散惯量模型中的频散效应和局部振荡效应。

4.1 频散效应

根据上文分析可知，5.514 Hz(0.2ωc)是本系统频散效应的门槛值。为验证频散现象与转折频率的关系，引入两组频率组合型的有功功率扰动信号P1和P2，分别表示为

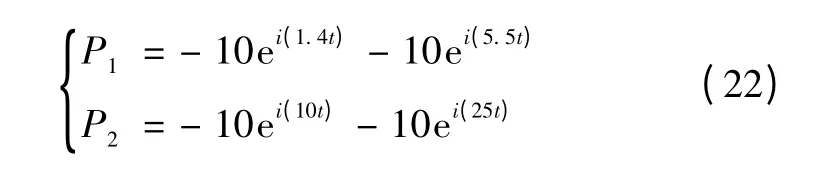
P1中的两个扰动频率分别为1.4 Hz 和5.5 Hz，均小于0.2ωc;P2中的两个扰动频率分别为10 Hz 和25 Hz，均大于0.2ωc。仿真结果如图5所示。

图5 扰动传播过程中的频散效应Fig.5 The frequency dispersion of disturbance propagations

图5中沿纵坐标从上至下分别为发电机G0～G49的转子角变化曲线。由于P1中的扰动频率均小于0.2ωc，尽管图5a 中各发电机转子角曲线变化周期较长，变化程度较大，扰动传播过程中并未出现频散效应。而P2中的扰动频率均大于0.2ωc，图5b 中在2 s时刻当初始扰动传播至G12发电机时，已经开始出现频散效应，波形在继续传播过程中发生了明显的畸变(见图5b 中的椭圆标记区域)。

4.2 局部振荡

转折频率ωc是电网离散惯量模型中局部振荡的门槛值。图6为当扰动频率与转折频率的比值分别为0.8、1.0 和1.2时，50 机链式电网的前5 台发电机的转子角增量曲线。

由图6a 和图6b 可得，当扰动信号频率小于等于转折频率时，扰动传播过程中各发电机转子角增量几乎没有衰减，基本呈等幅振荡。由图6c 可得当扰动信号频率大于转折频率时，沿扰动传播方向上各发电机的转子角增量幅值迅速衰减至稳态值，与本文所提出的局部振荡现象一致。

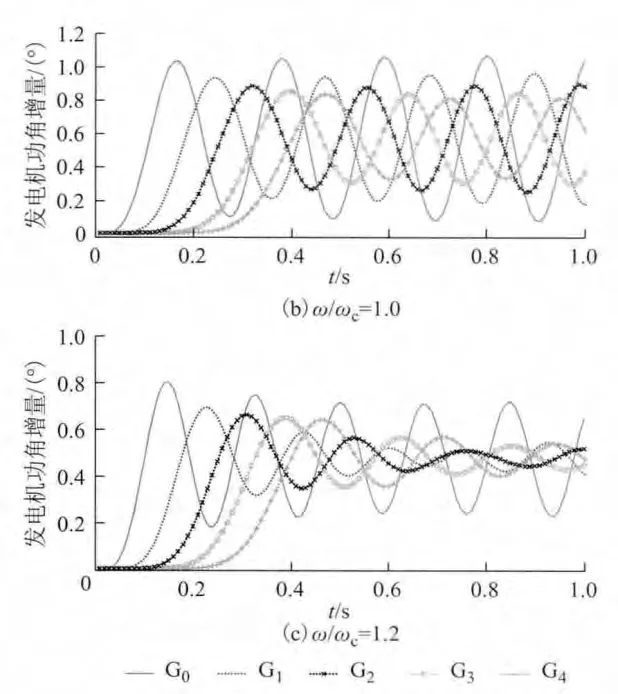
图6 扰动入射波的局部振荡现象Fig.6 The local oscillations of incident wave of disturbances

5 结论

本文针对具有简化发电机及线路模型的一维链式电网，从扰动频率和电网参数角度入手研究了离散惯量系统中扰动传播问题，提出了链式电网中用于判定扰动传播过程中幅值变化规律的转折频率ωc的概念。按照转折频率可将电网扰动信号划分为ω≤0.2ωc，0.2ωc＜ω ＜ωc和ω≥ωc三个频段。指出当扰动信号频率属于不同频段时，在扰动传播过程中将发生不同现象。

扰动信号的高频分量(ω≥ωc)在传播过程中会迅速衰减，因而其影响范围有限，说明发电机具有滤除高频扰动信号的作用。中频扰动信号(0.2ωc＜ω ＜ωc)能在电网中传播，但会发生频散效应，导致传播过程中波形的畸变。低频扰动信号(ω≤0.2ωc)则能持续在电网中传播且保持波形不变。

虽然本文的研究对象是一维链式电网，但实际电网中的扰动传播现象(如转折频率、频散效应和局部振荡现象等)有类似一维情形之处。本文阐明的机理有助于从根本上认识实际电网中扰动传播规律，对于开展电网扰动影响预测及基于扰动传播理论的电网安全控制方法研究具有的启发意义。

［1］ 吴晋波，文劲宇，孙海顺，等．基于储能技术的交流互联电网稳定控制方法［J］．电工技术学报，2012，27(6):261-267．

Wu Jinbo，Wen Jinyu，Sun Haishun，et al．Study of control method for improving AC interconnected grid stability based on energy storage technology［J］．Transactions of China Electrotechnical Society，2012，27(6):261-267．

［2］ Tamronglak S，Horowitz S H，Phadke A G，et al．Anatomy of power system blackouts:preventive relaying strategies［J］．IEEE Transactions on Power Delivery，1996，11(2):708-715．

［3］ De La Ree J，Liu Y L，Mili L，et al．Catastrophic failures in power systems:causes，analyses，and countermeasures［J］．Proceedings of the IEEE，2005，93(5):956-964．

［4］ Cresa P R，Hauer J．Emergence of a new swing mode in the western power system［J］．IEEE Transactions on Power Apparatus and Systems，1981，PAS-100(4):2037-2045．

［5］ 毕天姝，燕跃豪，杨奇逊．基于分段均匀介质模型的非均匀链式电网扰动传播机理研究［J］．中国电机工程学报，2014，34(7):1088-1094．

Bi Tianshu，Yan Yuehao，Yang Qixun．Disturbance propagation mechanism in non-uniform chained power networks based on sectionalized homogeneous medium model［J］．Proceedings of the CSEE，2014，34(7):1088-1094．

［6］ Thorp J S，Seyler C E，Phadke A G．Electromechanical wave propagation in large electric power systems［J］．IEEE Transactions on Circuits and SystemsⅠ:Fundamental Theory and Applications，1998，45(6):614-622．

［7］ Parashar M，Thor P J，Seyler C．Continuum modeling of electromechanical dynamics in large-scale power systems［J］．IEEE Transactions on Circuits and SystemsⅠ:Regular Papers，2004，51(9):1848-1858．

［8］ Nutaro J，Protopopescu V．A new model of frequency delay in power systems［J］．IEEE Transactions on Circuits and Systems II:Express Briefs，2012，59(11):840-844．

［9］ Semlyen A．Analysis of disturbance propagation in power systems based on a homogeneous dynamic model［J］．IEEE Transactions on Power Apparatus and Systems，1974，PAS-93(2):676-684．

［10］ 王德林，王晓茹，Thor P J．电力系统的连续体系机电波模型［J］．中国电机工程学报，2006，26(17):30-37．

Wang Delin，Wang Xiaoru，Thor P J．Electromechanical wave continuum model for power system［J］．Proceedings ofthe CSEE，2006，26(17):30-37．

［11］ Tsai S J，Zhang Li，Phadke A G，et al．Frequency sensitivity and electromechanical propagation simulation study in large power systems［J］．IEEE Transactions on Circuits and Systems I:Regular Papers，2007，54(8):1819-1828．

［12］ Dersin P，Levis A．Feasibility sets for steady-state loads in electric power networks［J］．IEEE Transactions on Power Apparatus and Systems，1982，PAS-101(1):60-70．

［13］ 王德林，郭成．电力系统连续体和离散模型中机电扰动传播的一致性研究［J］．电工技术学报，2012，27(6):161-167．

Wang Delin，Guo Cheng．Study on consistency of electromechanical disturbance propagation in continuum and discrete-models for power systems［J］．Transactions of China Electrotechnical Society，2012，27(6):161-167．

［14］ Thor P J，Seyler C，Parashar M，et al．The large scale electric power system as a distributed continuum［J］．IEEE Power Engineering Review，1998，18(1):49-50．

［15］ 吴晋波，文劲宇．基于机电波传播理论的柔性功率调节器稳定控制方法实验研究［J］．电工技术学报，2012，27(3):205-211．

Wu Jinbo，Wen Jinyu．Test on stability control method of the flexible power conditioner based on electromechanical wave propagation［J］．Transactions of China Electrotechnical Society，2012，27(3):205-211．

［16］ Yong Y，Lin Y．Dynamic response analysis of truss-type structural networks:a wave propagation approach［J］．Journal of Sound and Vibration，1992，156(1):27-45．