负荷按容分配的无线并联逆变系统收敛性分析

刘 斌 卢雄伟 熊 勇 谢积锦 伍家驹

(1.南昌航空大学信息工程学院 南昌 330063 2.科华恒盛股份有限公司 厦门 361006 3.钦州学院物理与电子工程学院 钦州 535000)

0 引言

随着国民经济的发展，电力需求也在迅速增长，但一味地扩大电网规模不能满足电力供应的要求。20世纪60年代的几次大型停电事故引发了科研人员对分布式发电系统潜在效益的重视。分布式电源尽管优点突出，但它相对于电网而言是一个不可控源，微电网便是在这种环境下应运而生的。它从系统角度出发将分布式电源、负荷、储能装置及控制装置等模块看成一个单一可控的单元，既可与电网联网运行，也可在电网出现故障或系统需要脱网时与主网断开单独运行。微电网的这种灵活可调度性，使得它可以成为未来大型电网的有力补充和有效支撑，因此，近年来关于微电网的研究引起了社会和学术界的广泛关注［1-4］。

在微电网控制策略中，最常见的有3 种［5，6］，即在并网运行时采用PQ 控制，在孤岛运行时采用V/f控制或下垂(droop)控制。由于本文侧重考虑的是微电网孤岛运行时的负荷分配问题，而基于单个V/f 微电源主从控制方式对主控电源的容量要求较高，整个微电网对主电源依赖性过高，因此最终选用基于下垂控制的微电源对等控制方式作为本文负荷分配的控制策略。

此外，依据逆变器之间是否存在互联线，可将逆变器并联技术分为有互联线并联和无互联线并联两大类，前者因为有互联线的存在而限制了逆变器模块之间的距离，相比而言无互联线并联技术具有更好的发展前景。其中，实现无互联线并联技术［7，8］的关键是按照输出电压幅值和频率与输出功率之间的下垂特性来调节系统给各逆变器模块所分配的负荷。

在国内关于无互联线并联技术的研究大多集中在同等功率等级的逆变器，这种传统并联技术要求系统实现功率均分。对于非同等功率等级的逆变器无线并联技术而言，因为均分系统负荷可能导致小容量逆变器无法工作，所以必须让负荷按照正比于逆变器模块容量的方式实现分配，这是近年来微电网研究的一个热点。国外相关的结论不多，国内就更少，远未达到完善的地步。

本文在介绍微电网结构和下垂控制原理［9］的基础上，首先通过对输出电压幅值和频率的收敛性分析推导出系统稳定的临界条件。然后，在系统控制器设计中，介绍了虚拟阻抗法［10］和双环调节器［11］。针对整流非线性负载引起的电压畸变问题，本文采用准谐振调节器进行谐波补偿。最后，为验证以上结论与策略的正确性，利用MATLAB/Simulink 进行了仿真，并搭建了由两台不同容量逆变器组成的实验平台。实验结果表明，通过调整下垂系数和虚拟阻抗可以较好地实现按逆变器容量分配负荷的目标。

1 微电网结构

图1为一种典型的微电网结构。从图中可以看出，一方面由于分布式电源与交流母线之间的传输距离较远且长度不一，因此线路阻抗不可忽略。另一方面由于分布式电源的容量有可能不一致，均分负荷的控制方法将严重限制微电网的潜力，因此本文的控制目标是依据电源容量按比例分配负荷。此外，在实际的微电网系统中，为了更加充分地利用分布式电源的发电量，往往需要通过K5来实现微电网与大电网之间的能量交换。然而由于本文侧重分析的是并联逆变负荷按容分配的问题，因此下文将围绕微电网处于脱网运行状态的情形展开讨论。

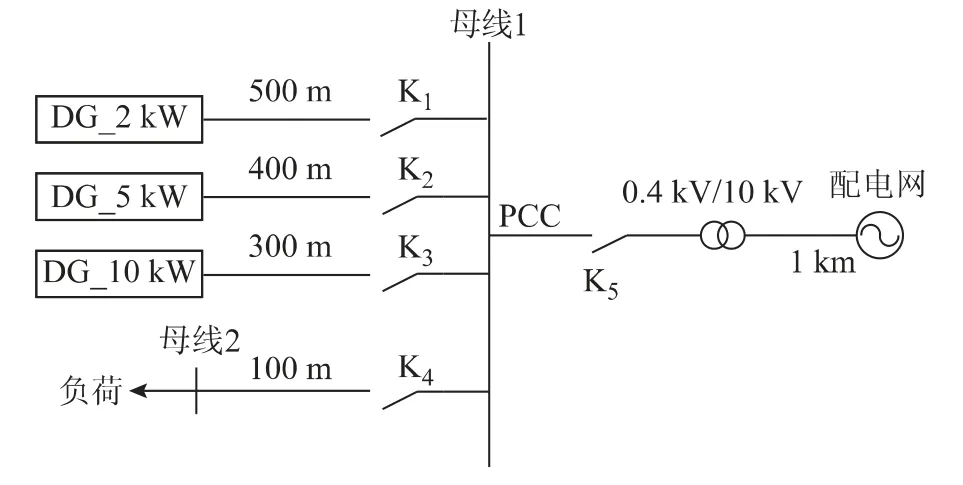
图1 微电网结构Fig.1 The microgrid structure

2 下垂控制原理

图2为逆变器并联系统的简化模型。其中Ei为第i 台逆变器输出电压的幅值(i=1，2)，σi为第i 台逆变器输出电压Ei相对于交流母线电压Eo的相位，Zi为第i 台逆变器等效输出阻抗，Z 为公共负载阻抗，Si、Pi和Qi分别为第i 台逆变器输出的复功率、有功功率和无功功率。

图2 逆变器并联系统模型Fig.2 A simplified model of the inverter parallel system

目前在逆变器的输出阻抗设计上有3 种选择，即阻性、感性和阻感性［12，13］。设计为纯阻性，在工程上易于实现，且可提高非线性负载的功率分配准确度;设计为纯感性，则在非线性负载时会使等效阻抗变大，使逆变器输出电压的总谐波畸变率(THD)增加，从而降低电能质量;设计为阻感性混合，则提高了控制的复杂程度［14］。因此，本文将等效输出阻抗设计为阻性，近似取Zi=Roi。

此外，由于本文讨论的负荷分配问题同时包含有功功率和无功功率，故将公共负载阻抗Z 设计成阻感性负载，即第i 台逆变器的输出电流Ii滞后交流母线电压Eo。

图3为第i 台逆变器的输出电压Ei与交流母线电压Eo的相位关系［15］(i=1，2 )。

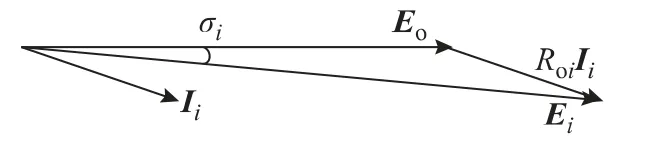
图3 相位关系图Fig.3 The phase diagram

从图3可看出，逆变器的输出复功率为

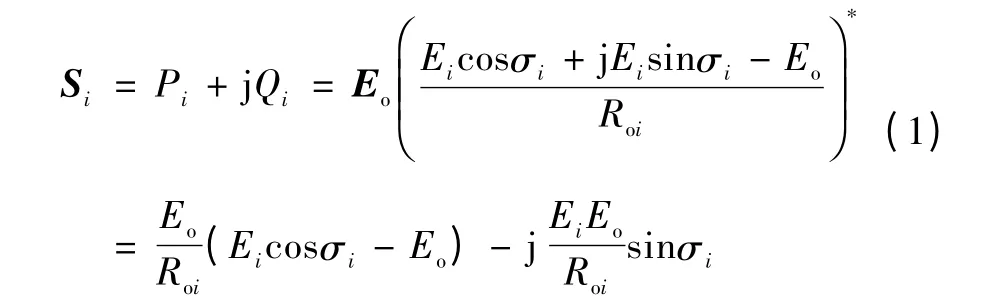
此外，由于实际的功率角σi很小，近似取cosσi=1，sinσi=σi，则有

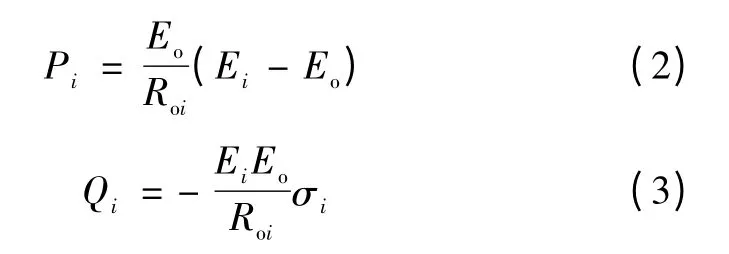
从式(2)可以看出，在等效输出阻抗呈阻性时，有功功率的变化主要由电压幅值Ei决定，无功功率的变化主要由电压相位σi决定，因此通过分别调整Ei与σi便可实现对有功无功的控制。此外，由于相位不方便直接进行控制，而频率的积分等于相位，因此可以通过调整频率来间接控制相位。所以，最终的下垂控制方程为

式中:E*和ω*分别为两台逆变器输出电压幅值和频率的给定;ni和mi分别为第i 台逆变器的有功和无功下垂系数。

图4为功率下垂控制示意图。在阻性阻抗时，由式(4)、式(5)可知，当逆变模块输出有功较大时，可以通过下垂控制使其幅值减小，从而引起有功功率的减小，最终达到并联系统有功功率的平衡;当逆变模块输出无功较大时，通过下垂算法控制其相位增大，从而引起无功功率的下降，最终达到并联系统无功功率的平衡。

图4 功率下垂控制示意图Fig.4 The control schematic of power droop

由式(2)～式(5)可以得到下垂控制框图，如图5所示。图中为经下垂后合成的参考正弦值，uo和io分别为逆变器的输出电压和电流信号。

3 系统收敛性分析

3.1 比例分配有功

本节将从单台分布式电源电压幅值收敛的条件、稳态时两台分布式电源电压幅值相等的条件及有功功率与分布式电源额定容量成正比的条件3 个方面对比例分配有功进行收敛性分析。此外，由式(4)进一步可推知，电压幅值收敛等效于有功的收敛，而稳态时两台电源电压幅值相等是实现按容分配有功的前提条件。

首先，分析单台分布式电源电压幅值收敛的条件，由式(1)和式(4)可以得到系统关于有功功率和电压幅值的瞬时表达式

由式(8)和式(9)，进一步得到变量Eik相对于稳态量偏差的迭代式

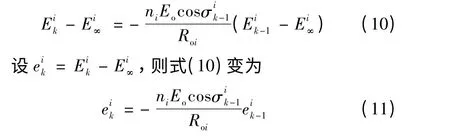
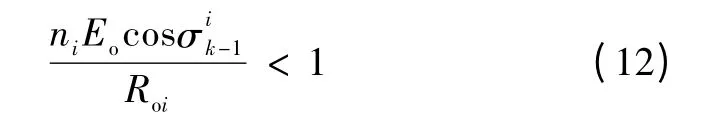
接下来，分析稳态时两台分布式电源电压幅值相等的条件。由式(9)可知，稳态时分布式电源电压幅值可表示为

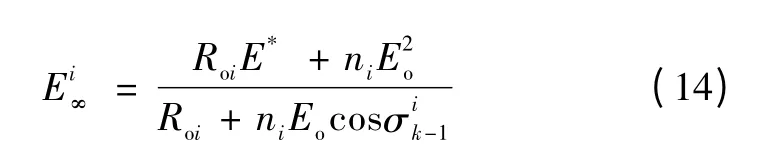
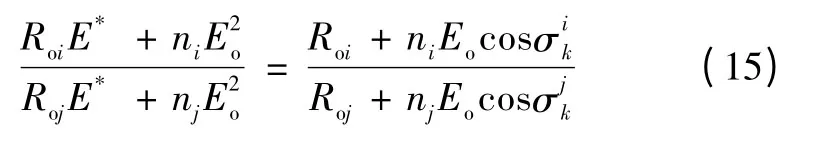
然而，使式(15)成立的充分条件是

最后，分析有功功率与分布式电源额定容量呈正比的条件。由于所有逆变器输出电压幅值的给定E*相同，且系统稳定后有Ei=Ej，故从式(4)可推知

假设有功下垂系数n 满足

式中S*为分布式电源的额定容量。联合式(17)和式(18)便可推知有功功率与分布式电源额定容量呈正比关系

综上所述，虽然在以上推导过程中出现的公式较多，但是可以看出，式(8)和式(9)是所有推导的出发点，而式(10)和式(15)分别是实现系统收敛和按容分配负荷的关键公式。同时也可以得出以下结论，即单个分布式电源电压幅值的收敛条件为有功下垂系数的取值受到线路阻抗和额定电压的限制，如式(13)所示。实现比例分配有功的条件为有功下垂系数和输出阻抗均与模块容量成反比。

3.2 比例分配无功

同理，本节将从单台分布式电源电压频率收敛的条件、稳态时两台分布式电源电压频率相等的条件及无功功率与分布式电源额定容量呈正比的条件3 个方面对比例分配无功进行收敛性分析。此外，由式(5)进一步可推知，电压频率收敛等效于无功的收敛，而稳态时两台电源电压频率相等是实现按容分配无功的前提条件。

首先着重分析单台分布式电源电压频率收敛的条件。设ωk为第k时刻逆变器的频率，为第k时刻公共负载电压的频率，σk+1和σk分别为逆变器在第k时刻和第k+1时刻相对于公共负载电压的相位差，则相位差σ 的动态变化过程可由图6表示。

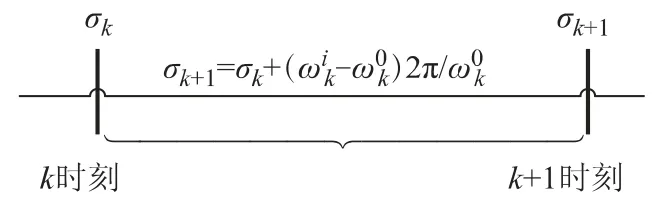
图6 σk的动态变化过程Fig.6 The dynamic changing process of σk

也即

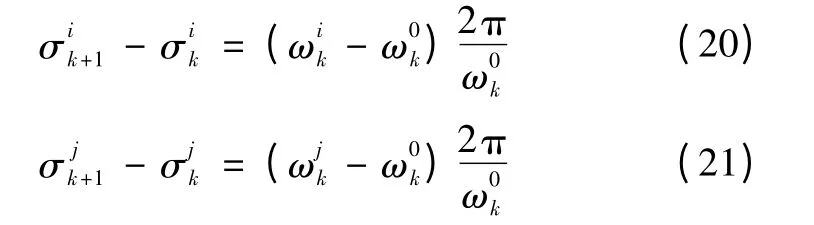
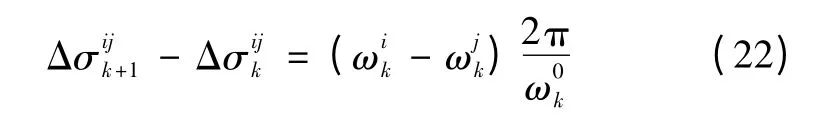
然后由式(3)与式(5)可推出逆变器i 和j 在第k时刻的频率差值为

此外，从第3.1 节可知，稳态时Ei≈Ej≈E，再，则式(23)变为

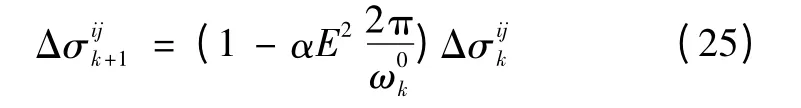
需要说明的是，本文讨论的范围是在比例分配有功的基础上实现比例分配无功。由式(3)可知，逆变器的无功大小主要由线路阻抗Roi和逆变输出电压相对于公共负载电压的相位差σi决定。更准确地说，是与线路阻抗Roi呈反比，与相位差σi呈正比。从第3.1 节可知，线路阻抗与模块容量已经设计呈反比，因此各逆变器只有在σi相等(即趋于零)时才能实现按比例分配无功。

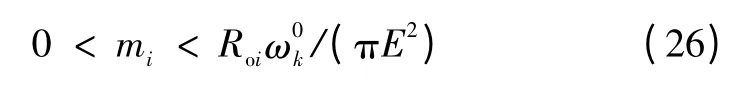
接下来，分析无功功率与分布式电源额定容量呈正比的条件。由于所有逆变器输出电压频率的给定ω*相同，且系统稳定后有ωi=ωj，故从式(5)可推知

假设无功下垂系数m 满足

式中S*为分布式电源的额定容量。联合式(27)和式(28)便可推知有功功率与分布式电源额定容量呈正比关系

综上所述，虽然在以上推导过程中出现的公式较多，但可看出式(22)和式(24)是所有推导的出发点。同时也可得出以下结论，即单个分布式电源电压频率收敛的条件为无功下垂系数的取值受到线路阻抗和额定电压的限制，如式(26)。实现比例分配无功的条件为无功下垂系数与模块容量呈反比。

4 系统控制器设计

系统的硬件部分选用单相全桥，后级加入LC 滤波器以消除输出电压中的高次谐波。

软件部分包括锁相环、功率计算环、下垂控制器、虚拟阻抗环和双环调节器等环节。其中，锁相环是用来实现逆变电源之间相位的同步。虚拟阻抗环以输出电流作为输入，用来校正输出阻抗近似成比例，从而满足负荷分配的要求。下垂控制器以锁相信号和功率计算结果作为输入，产生初始给定信号，再减去虚拟阻抗环的输出，便得到最终的逆变电压给定信号。系统的主控制器，以逆变电压给定信号作为输入，以电感电流和电容电压作为反馈，构建成电压外环电流内环的双环调节器，用来产生单相全桥的驱动信号。

当系统只为线性负载供电时，逆变器闭环控制的传递函数可等效为

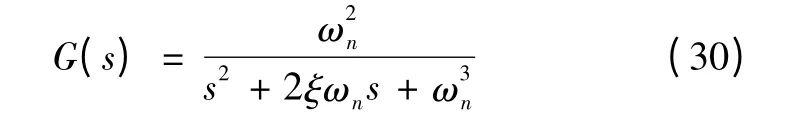
此时的逆变器系统是标准二阶系统。只要将阻尼比ξ 的取值范围约束在0．4～0．8(通常取0.707)，同时将ωn选择在既要足够大又要小于电力电子器件开关频率的取值范围(可选择1 000 rad/s)，那么系统便可获得较好的时域和频域性能。

然而，当系统带RCD 或其他非线性负载时，电流中的谐波成分将通过虚拟阻抗引入电压给定，从而导致输出电压畸变。由于谐波电流主要集中在3、5、7、9 次，因此可考虑在双环调节器的电压外环上并联准谐振调节器来补偿特定次谐波。式(31)为准谐振调节器的通用表达式。

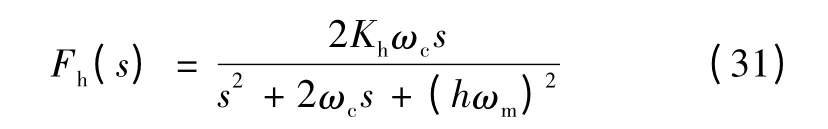
式中:Kh为准谐振调节器的比例系数;ωc为带宽;ωm为中心频率。

虽然准谐振调节器具有一定带宽，但即使给定频率偏移中心频率只有0.5 Hz，补偿效果也将大打折扣。因此非常有必要使准谐振调节器具有自适应性，即让ωm跟随下垂后变化的给定频率ωi。

本文侧重于讨论非同等功率等级的逆变器并联的收敛性分析。至于自适应准谐振调节器的实现方法，由于文献［16］中已出现较完善的方法，所以不再具体讨论。

5 仿真及实验验证

5.1 仿真验证

为了验证以上的理论分析，利用MATLAB 软件构建了一个仿真平台，设计两台额定容量比为1∶2 的逆变器并联运行(其中，DG1 的容量为2 kW，DG2 的容量为4 kW)。

仿真参数如下:DG1 的线路阻抗为0.1+j0.031 Ω，DG2 的线路阻抗为0.2+j0.016 Ω;DG1 的虚拟阻抗Rv1为1.9 Ω，DG2 的虚拟阻抗Rv2为0.8 Ω;负载阻抗为8+j1.57 Ω。

仿真过程为:0～0.2 s 空载运行，0.2 s时投入负载。

从图7中4 组波形的对比可发现，A 组，有功和无功的下垂系数均大于临界值，对应于仿真波形则是有功和无功均不收敛;B 组，有功下垂系数大于临界值，无功下垂系数小于临界值，对应于仿真波形则是有功不收敛而无功收敛;C 组，有功下垂系数小于临界值，无功下垂系数大于临界值，对应于仿真波形则是有功收敛而无功不收敛;D 组，有功和无功的下垂系数均小于临界值，对应于仿真波形则是有功和无功均收敛。因此仿真结果可验证第3 节的结论，即单个分布式电源电压幅值收敛的条件为有功下垂系数小于临界值(由式(13)计算可得);单个分布式电源电压频率收敛的条件为无功下垂系数小于临界值(由式(26)计算可得)。

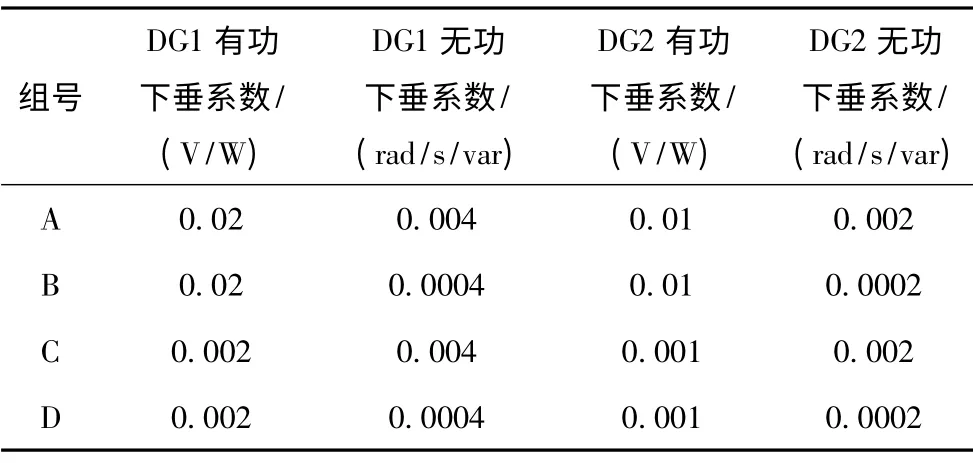
表14 组不同的有功和无功下垂系数Tab.1 Four different sets of active and reactive power droop factor

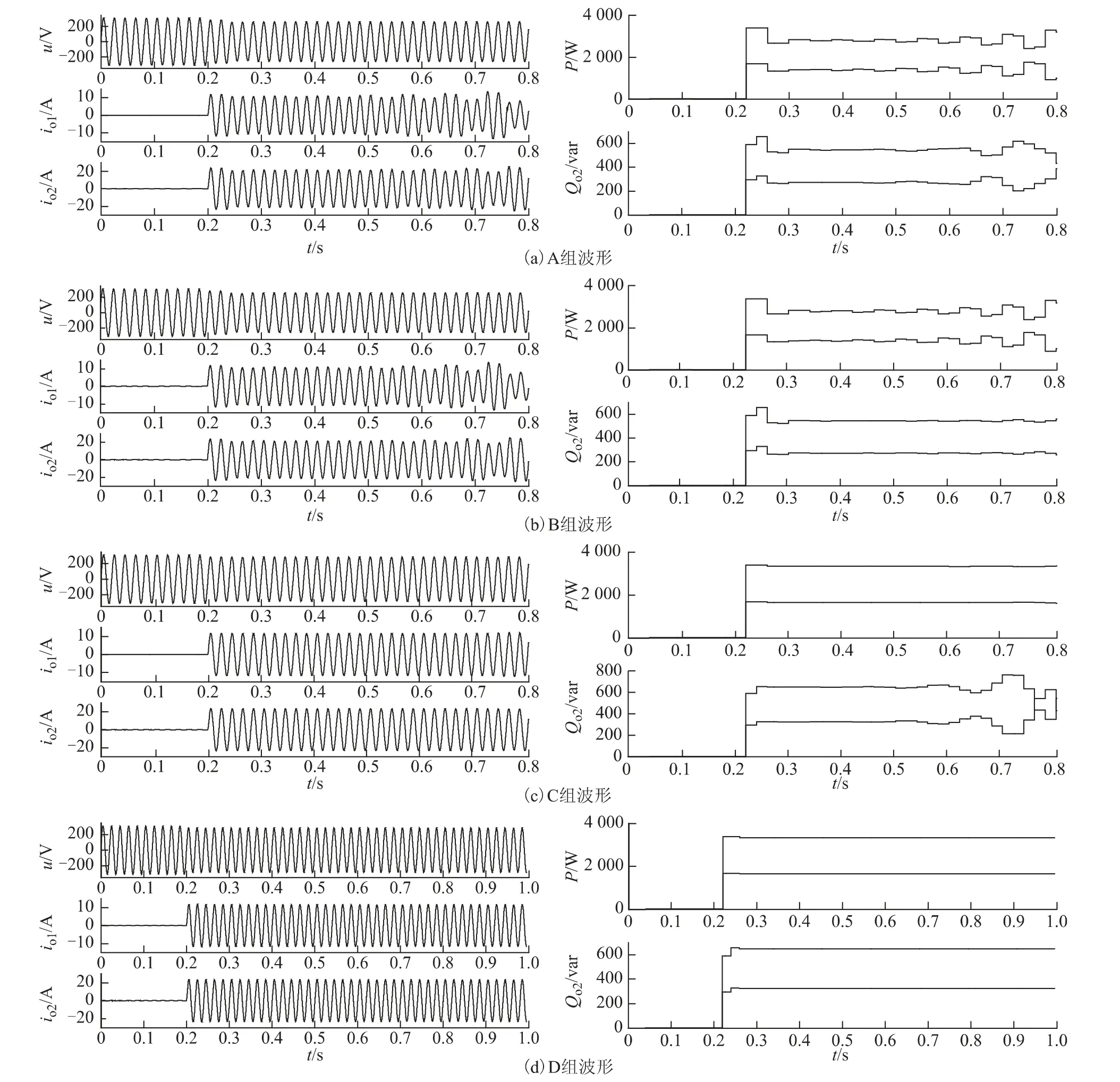
图7 A、B、C、D 组下垂系数对应的电压电流波形和有功无功波形Fig.7 The waveform of voltage，current，active power and reactive power correspond to the droop coefficient of group A，B，C，D

从式(13)和式(26)可知，由于有功下垂系数ni和无功下垂系数mi的临界值均与稳态电压幅值Eo有关，因此ni与mi之间存在耦合，也即当ni和mi中任一系数超出临界值时，则会引起电压幅值偏离稳态值Eo，进而导致临界值出现变动，假如另一系数的裕量较小，那么将导致另一功率也不再收敛，图7中的4 组有功和无功波形也验证了这一分析结论。综上所述，保证系统有功功率收敛的充分条件，除了要求有功下垂系数小于临界值之外，还需要保留一定的裕量来克服无功下垂系数对它的影响;而无功功率收敛的情形也存在同样的要求。

此外，当系统带整流性负载(阻抗为15－j3.185 Ω)时，为了改善交流母线电压THD，添加一个准谐振调节器进行谐波补偿。从图8a 与图8b 的对比可看出，添加准谐振调节器后，畸变的交流母线电压得到补偿，而实测的交流母线电压THD 也由7.01%降为3.16%。

图8 系统带整流性负载时，有无谐波补偿的仿真波形Fig.8 When the system with a rectifier load，the simulation waveforms with and without harmonic compensation

5.2 实验验证

为了对仿真结果进行验证，搭建了由两台不同容量逆变器组成的实验平台，图9为逆变器的实物图。主电路拓扑为单相全桥，控制芯片为TMSF2802 DSP，载波频率为19.2 kHz。

图9 逆变器的实物图Fig.9 The inverter physical map

在本次实验中，逆变器DG1 与DG2 的输出电压有效值均为110 V，两者并联之后，经过一个1∶2 的工频变压器与负载相连，其中公共负载阻抗为16 Ω，可计算出并联系统的总功率为3 kW。设计目标为DG1与DG2分配负荷之比为1∶2。在控制器中，将DG1 与DG2 的虚拟阻抗分别设置为3 Ω 和1.5 Ω，可计算出收敛的临界下垂系数分别为n1≈0.002 V/W，m1≈0.012 rad/s/var，n2≈0.001 V/W，m2≈0.006 rad/s/var。在程序中，取m1≈0.001 2 rad/s/var，m2≈0.000 6 rad/s/var，为了验证有功下垂系数对电压幅值收敛性的影响，将两台逆变器有功下垂系数的初值分别设置为0.002 V/W 和0.001 V/W。然后等待系统稳定工作10 s 左右，便将有功下垂系数分别调整为0.06 V/W 和0.03 V/W，此时并联系统的实验波形将出现振荡现象，如图10a 所示。接着让系统在振荡状态下工作2 s 左右，便将有功下垂系统回归初值，此时并联系统的实验波形将恢复稳定状态，如图10b 所示。因此，实验结果也可以验证第3 节关于系统收敛性分析的结论。

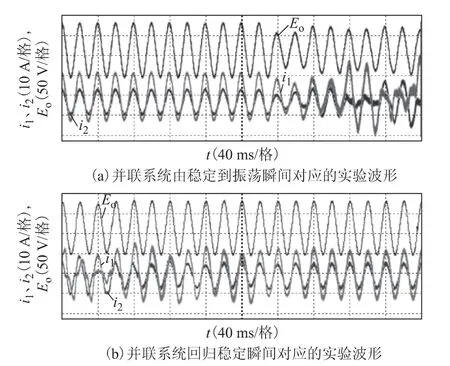
图10 并联系统发散和收敛过程对应的实验波形Fig.10 The experimental waveforms when the divergence and convergence process of the parallel system

此外，为了验证准谐振调节器改善交流母线电压THD 的效果，做了一个添加准谐振调节器前后的对比实验，如图11所示。从实验波形可看出，畸变的交流母线电压得到补偿，而实测的THD 也由7.05% 降为3.28%。

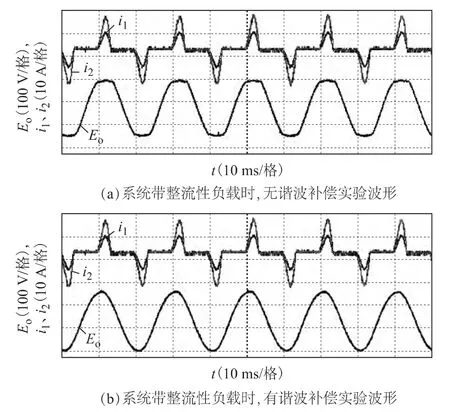
图11 系统带整流性负载时，有无谐波补偿的实验波形Fig.11 When the system with a rectifier load，the experimental waveforms with and without harmonic compensation

6 结论

本文围绕功率下垂控制原理对逆变器并联系统的按容分配负荷问题展开了讨论。首先，通过对输出电压幅值和频率进行收敛性分析，推导出系统稳定的临界条件。然后引入虚拟阻抗环和双环调节器构建一个微电网系统的仿真平台，对理论分析进行了相关验证，从图7中4 组波形的对比可知，单个分布式电源电压幅值收敛的条件为有功下垂系数小于临界值，单个分布式电源电压频率收敛的条件为无功下垂系数小于临界值。此外针对整流非线性负载引起输出电压畸变问题，本文采用准谐振调节器进行谐波补偿，图8中的2 组仿真波形可说明补偿效果。最后搭建的实验平台也对仿真结果进行了相应的验证。

［1］ 王成山，武震，李鹏．微电网关键技术研究［J］．电工技术学报，2014，29(2):1-12．

Wang Chengshan，Wu Zhen，Li Peng．Research on key technologies of microgrid［J］．Transactions of China Electrotechnical Society，2014，29(2):1-12．

［2］ 刘文，杨慧霞，祝斌．微电网关键技术研究综述［J］．电力系统保护与控制，2012，40(14):152-155．

Liu Wen，Yang Huixia，Zhu Bin．Survey on key technologies of microgrid［J］．Power System Protection and Control，2012，40(14):152-155．

［3］ 杨新法，苏剑，吕志鹏，等．微电网技术综述［J］．中国电机工程学报，2014，34(1):57-70．

Yang Xinfa，Su Jian，Lv Zhipeng，et al．Overview on micro grid technology［J］．Proceedings of the CSEE，2014，34(1):57-70．

［4］ Guerrero J M，Vasquez J C，Matas J，et al．Control strategy for flexible microgrid based on parallel lineinteractive UPS systems［J］．IEEE Transactions on Industrial Electronics，2009，56(3):726-736．

［5］ 廖扬帆，王家华，许健，等．微电网的自适应组网技术［J］．电子测试，2014(2):140-141．

Liao Yangfan，Wang Jiahua，Xu Jian，et al．Adaptive network technology of the micro grid［J］．Electronic Test，2014(2):140-141．

［6］ 舒海莲．微电网运行特性及其控制研究［D］．上海:上海电力学院，2011．

［7］ 吕世家，罗耀华．无互联线逆变器并联控制技术［J］．应用科技，2010，37(5):52-55．

Lv Shijia，Luo Yaohua．Inverter parallel system by wireless control technology［J］．Applied Science and Technology，2010，37(5):52-55．

［8］ 张尧，马皓，雷彪，等．基于下垂特性控制的无互联线逆变器并联动态性能分析［J］．中国电机工程学报，2009，29(3):42-48．

Zhang Yao，Ma Hao，Lei Biao，et al．Analysis ofdynamic performance for parallel operation of inverters without wire interconnections［J］．Proceedings of the CSEE，2009，29(3):42-48．

［9］ 姚玮，陈敏，牟善科，等．基于改进下垂法的微电网逆变器并联控制技术［J］．电力系统自动化，2009，33(6):77-80．

Yao Wei，Chen Min，Mu Shanke，et al．Paralleling control technique of microgrid inverters based on improved droop method［J］．Automation of Electric Power Systems，2009，33(6):77-80．

［10］ 鲍薇，胡学浩，李光辉，等．独立型微电网中基于虚拟阻抗的改进下垂控制［J］．电力系统保护与控制，2013，41(16):7-13．

Bao Wei，Hu Xuehao，Li Guanghui，et al．An improved droop control strategy based on virtual impedance in islanded micro-grid［J］．Power System Protection and Control，2013，41(16):7-13．

［11］ 朱承邦，李乐，王晓鹏．基于SPWM 控制的电压电流双环逆变器建模及其仿真［J］．中国舰船研究，2009，4(5):54-58．

Zhu Chengbang，Li Yue，Wang Xiaopeng．Based SPWM control voltage，current bicyclic inverter modeling and simulation［J］．Chinese Journal of Ship Research，2009，4(5):54-58．

［12］ Yao W，Chen M，Matas J，et al．Design and analysis of the droop control method for parallel inverters considering the impact of the complex impedance on the power sharing［J］．IEEE Transactions on Industrial Electronics，2011，58(2):576-588．

［13］ 陈宏志，王旭，刘建昌，等．基于虚拟电阻匹配模式的逆变器并联方案［J］．中国电机工程学报，2012，32(6):25-32．

Chen Hongzhi，Wang Xu，Liu Jianchang，et al．Current sharing method for parallel inverters based impedance matching mode［J］．Proceedings of the CSEE，2012，32(6):25-32．

［14］ 王成山，肖朝霞，王守相．微网中分布式电源逆变器的多环反馈控制策略［J］．电工技术学报，2009，24(2):100-107．

Wang Chengshan，Xiao Zhaoxia，Wang Shouxiang．Multiple feedback loop control scheme for inverters of the micro source in microgrids［J］．Transactions of China Electrotechnical Society，2009，24(2):100-107．

［15］ 陈达威，朱桂萍．低压微电网中的功率传输特性［J］．电工技术学报，2010，25(7):117-122，143．

Chen Dawei，Zhu Guiping．Power transmission characteristics of low voltage microgrids［J］．Transactions of China Electrotechnical Society，2010，25(7):117-122，143．

［16］ 刘斌，谢积锦，李俊，等．基于自适应比例谐振的新型并网电流控制策略［J］．电工技术学报，2013，28(9):186-195．

Liu Bin，Xie Jijin，Li Jun，et al．Novel grid-connected current control strategies based on self-adaptive proportionalresonant［J］．Transactions of China Electrotechnical Society，2013，28(9):186-195．