微电网建设规划方案评估与选择

黄雄峰 翁 杰 张宇娇

(三峡大学电气与新能源学院 宜昌 443002)

0 引言

微电网建设规划方案需满足一定的投资可能性，因规划原理、技术路线、运行维护、经济状况和环境保护等不同，规划方案的种类会产生多样化［1，2］，这会导致指标体系呈现出高维、非线性的特性［3］，对指标关联关系的合理处理直接影响微电网建设规划方案评估的科学性，因此，如何有效地指出规划方案的薄弱环节，兼顾指标间的关联关系，使管理者做出合理的决策，具有重要的工程实用意义［4，5］。

目前对微电网建设规划进行综合评估决策的方法主要有模糊综合评价法、层次分析法、数据包络分析方法等。文献［6］提出了一种基于区间数的城市配电网经济运行模糊综合评价方法，利用区间层次分析法计算指标权重，解决了专家判断的不确定性。文献［7］将D-S 证据推理方法与传统的贝叶斯网络法相结合，进行配电系统的可靠性评估，能够很好地处理具有模糊和不确定信息的合成问题。上述方法明确了决策问题中的层次结构的模糊性和不确定性，但忽略了要素间的关联关系。文献［8］采用网络层次分析法对电网建设项目进行研究，单纯使用ANP 法虽然考虑了指标间的相互影响和相互联系，但要素间影响关系的刻画较为粗略和主观。决策问题中存在层次结构间的关联性，评价指标并非相互独立［9］，而上述微电网建设规划综合决策方法对评价指标要素间的关联关系或者予以忽略，或者考虑过于主观随意，因此，亟需找到一种可以实现关联关系准确度量的评判方法，通过对综合决策过程中评价指标之间相互影响关系的量化处理，有效解决关联关系难以界定的问题。

在充分考虑影响因素之间的依赖-反馈关系下，本文建立了一套多属性的微电网建设规划方案决策体系，形成科学完善的决策方法，通过追求最大化群体效益和最小化个体遗憾，实现对备选微电网建设规划方案的排序和选优，并运用实例计算验证了该决策方法的有效性。

1 评价指标体系

建立科学合理的指标体系是规划方案评估工作的重要前提。微电网建设规划中各项指标需达到一定的技术要求，同时还应综合考虑供电的可靠性、建设的经济性和环境的保护性等诸多影响因素［10］。以指标尽可能全面、不重叠、易于取得为准则，在熟悉评估目标的内涵与构成的基础上完成了评价指标体系的初选，然后结合功能聚合与相关性聚合对初选的指标体系进行结构优化，最后从可靠性、经济性、技术性和环境性四个方面建立了一套可以对微电网进行科学评估决策的指标体系。建立的微电网建设规划方案评价指标体系如图1所示。

从指标体系的构成可以看出因素之间存在相互影响:对规划方案投资过多会导致资源浪费，投资不足又将无法实现优化配置，这将直接影响建设方案的技术性指标;微电网技术性的投入不足将会造成微电网可靠性的降低。因此，评价指标间的关联关系是广泛存在的，而传统的评估标准和准确尺度却很难衡量或界定［11］，采用DEMATEL-ANP-VIKOR 混合决策模型，通过建立指标间的网络层次关系，可以准确反映影响因素的实际情况。

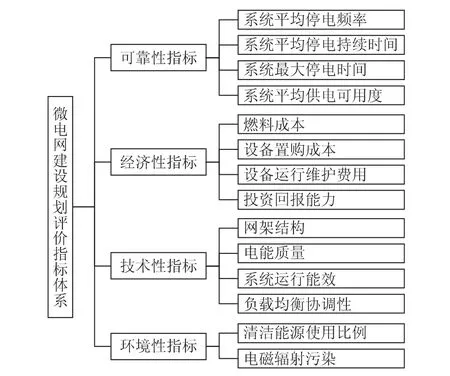
图1 评价指标体系Fig.1 Evaluation index system

2 基于DEMATEL-ANP-VIKOR 混合决策模型的评估决策

在微电网建设规划最优方案的优化选择中，首先采用DEMATEL 法量化准则层要素的影响关系强度;然后利用ANP 法确定准则层各指标的权重;最后结合VIKOR 法进行备选方案的排序和选优。

2.1 DEMATEL-ANP 建设规划评估

根据构建的评价指标体系，用DEMATEL 法建立综合影响关系矩阵，找出评价指标体系中指标间的关联关系，得到准则层要素的影响关系图，再结合专家分析的结论建立各准则下元素相互比较的判断矩阵，计算各指标对目标的权重分配，具体步骤如下［12，13］。

利用相关文献和专家评审结果对影响要素的相互关系进行分析，建立准则层要素的直接影响关系矩阵A

式中:aij为要素i 对要素j 的影响，aij=0、1、2、3、4;n 为准则层要素的数量。

将矩阵A 标准化

考虑要素之间的间接影响，计算综合影响关系矩阵T

在综合影响关系矩阵中，关联度较小的指标对ANP 法计算权重影响不大，通过设定门槛值p 来剔除关联度较小的关系，实现准则层要素之间的影响关系网络结构图的简化。

根据专家探讨的结果将ANP 网络层元素组中元素的相互影响力大小进行间接优势度比较，可形成各准则下元素之间的两两比较判断矩阵，再由特征根法计算权重向量，构造的未加权超矩阵W 形式为

式中:CN为ANP 网络层中的元素组;eNnN为元素组中的元素;Wij为Ci中元素对Cj中元素的影响力矩阵，Wij=0 表示Cj中的元素不受Ci中的元素影响。

为明确各元素组之间的相互影响关系，对超矩阵进行归一化处理。以元素组为研究对象，构造准则下各组元素对Cj的相对重要性判断矩阵，得到该元素组作为子准则下其他元素组的归一化的权重矢量［h1j，h2j，…，hnj］T。对于j=1，2，…，N，重复上述步骤，得到权重矩阵

构造加权超矩阵

对矩阵Wh求极限，得到极限超矩阵

若极限值收敛且惟一，则可得到列值相同、列和为1 的极限超矩阵，指标的权重即为极限超矩阵对应行的值。

2.2 VIKOR 规划方案决策

完成对备选方案各指标的评分后，结合上述DEMATEL-ANP 法计算得到的准则层指标权重，采用VIKOR 法对备选方案进行排序和选优，具体步骤如下［14-17］。

将方案指标的初始值标准化处理

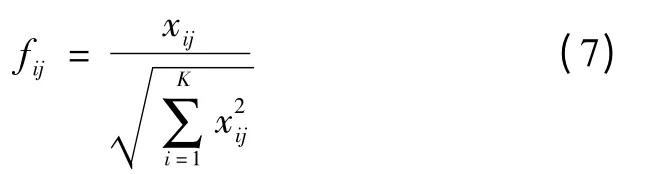
式中:xij为第i 个方案第j 个指标的评价值;K 为备选方案的数量。

式中:I1为效益型准则集合;I2为成本型准则集合。

得到第i 个评估方案的群体效益值Si和个体遗憾值Ri

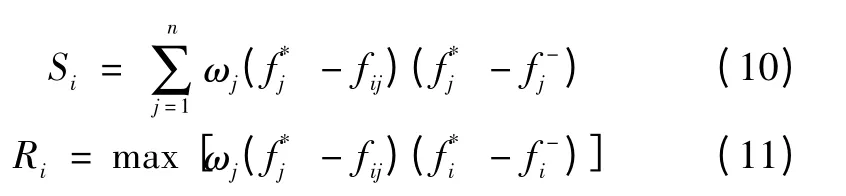
式中:ωj为第j 个指标的权重;Si值越小表示群体效益越大;Ri值越小表示个体遗憾越小。

考虑决策者的效用偏好，计算综合指标Qi的值为

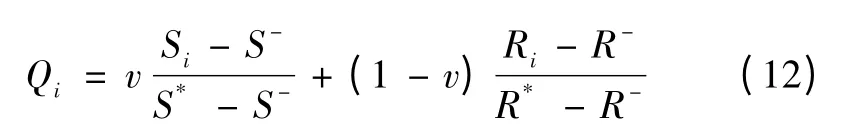
计算备选方案的Si、Ri和Qi值，并按由小到大排序，其中，Si、Ri和Qi值越小表示该方案表现越好。

结合理想方案的选取条件和评判准则［15，16］，对备选方案最优性进行验证，决策出Q 排列中的最优方案。

条件1:优势的可接受性。

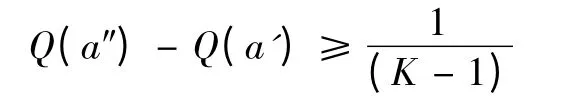
式中:a' 为Q 值最小的方案;a″为Q 值第二小的方案;K 为备选方案的数量。

条件2:决策可信度的可接受性。

方案a'的S 值小于方案a″的S 值，或方案a'的R值小于方案a″的R 值。

评判准则:若上述条件同时满足，则接受a' 为最优方案;若只满足条件2，则接受a' 和a″同为最优方案。当存在多个备选方案时，沿用上述选取条件及评判准则依次对其他方案的最优性进行验证，直到选出最优方案。

3 实例计算与分析

某地进行微电网项目建设，并给出了3 个规划方案。通过对备选方案进行评估，决策出最优的实施方案，以提高规划设计的科学性。3 个规划方案的相关指标评价值经过归一化处理后如表1 所示。

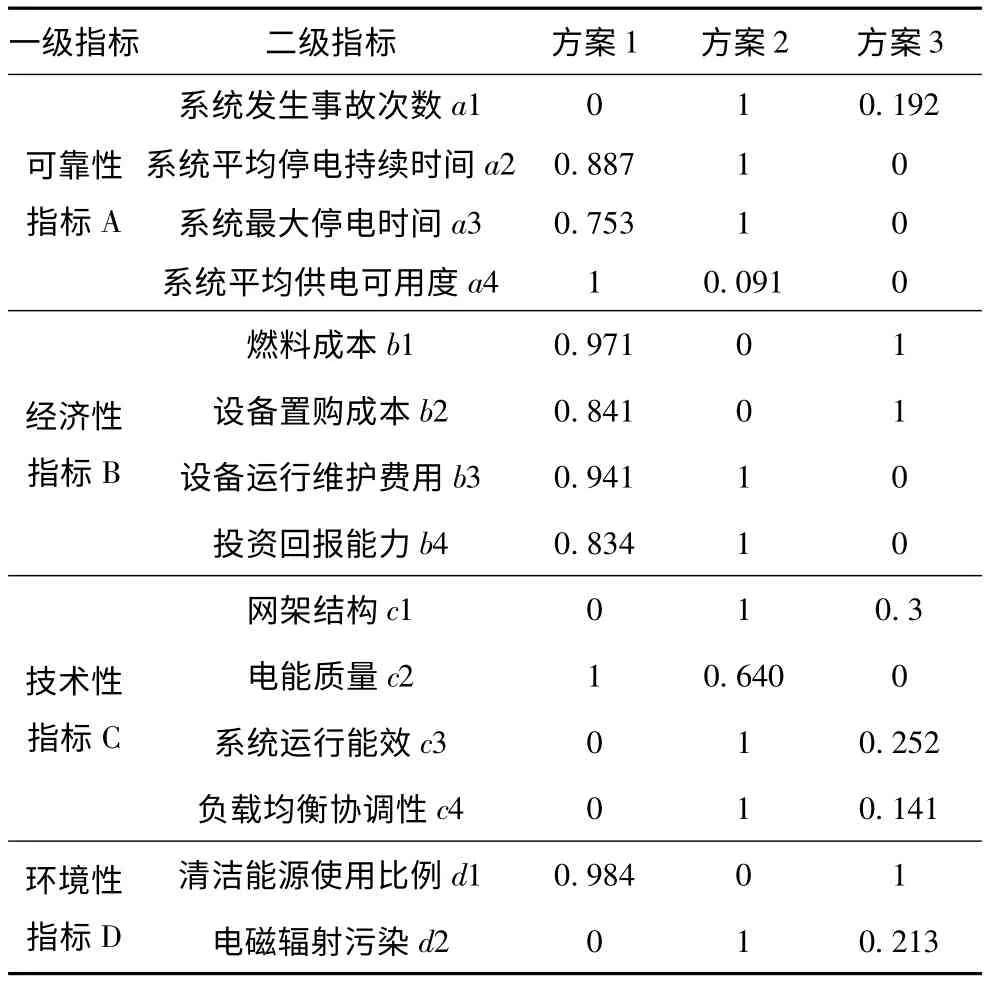
表1 备选方案指标的数据Tab.1 Data of the index to alternatives

1)准则层要素关系网络结构图。

将要素之间的影响强度分为无影响、低度影响、中度影响、高度影响和极高度影响5 个等级，分别用0、1、2、3、4 表示。4 位专家对两两要素的直接影响强度进行打分，平均打分结果，得到直接影响关系矩阵A，见表2。

表2 直接影响关系矩阵ATab.2 Matrix A of the direct influence relation

利用式(2)对直接影响关系矩阵标准化处理，再结合式(3)计算得到综合影响关系矩阵T(如表3 所示)，充分征求专家意见设定门槛值p=1．2，剔除影响度低于门槛值的关联关系(见表3 中的黑体数值)，得到微电网建设规划方案准则层要素间依赖-反馈关系的网络结构图，如图2所示(箭头方向表示由被影响者指向影响者)。

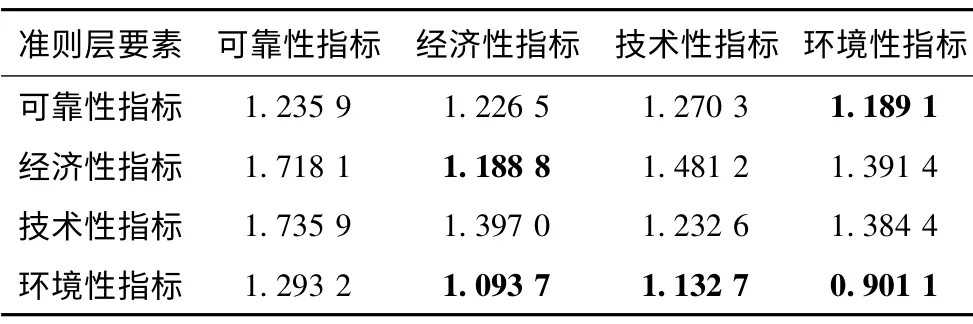
表3 综合影响关系矩阵TTab.3 Matrix T of the comprehensive influence relation

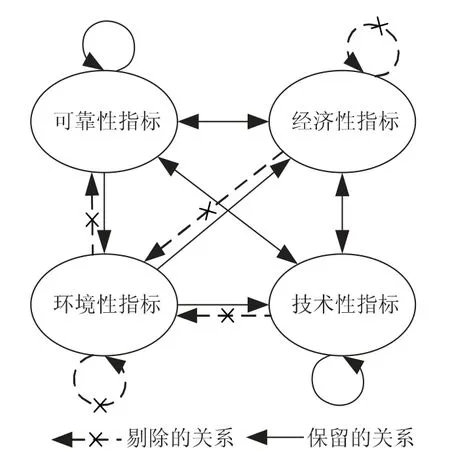
图2 准则层要素关系网络结构图Fig.2 The network structure of the criterion layer elements

2)指标权重分析。

结合准则层要素关系网络结构图，在专家打分结果的基础上建立判断矩阵，计算未加权超矩阵，加权超矩阵和极限超矩阵，得到对应的指标权重。与采用AHP 法对上述3 个方案进行评估的结果对比，如图3所示。

图3 ANP 法和AHP 法指标权重对比Fig.3 Weight contrast of ANP and AHP

ANP 法与AHP 法得到的指标权重在单个数值上有明显的不同，但其总体排序变化不大。指标权重排序分析:AHP 法注重环境指标对建设方案的影响，而ANP 法更强调经济效益的作用。指标权重离散度(即指标权重的标准差)分析:AHP 法为0.044 0，ANP 法为0.027 3，AHP 法的指标权重个体差异较大，而ANP 法的指标权重分配趋于均衡，体现了指标内部的依赖-反馈关系。通过考虑评价体系中复杂的影响关系，ANP 法对指标权重的衡量更为合理。

3)最优方案选择。

设定决策机制系数v=0．5，利用规划方案的相关指标评价值(见表1)计算出备选方案的Si、Ri以及Qi值，结果见表4(括号内的数字代表排序号)。

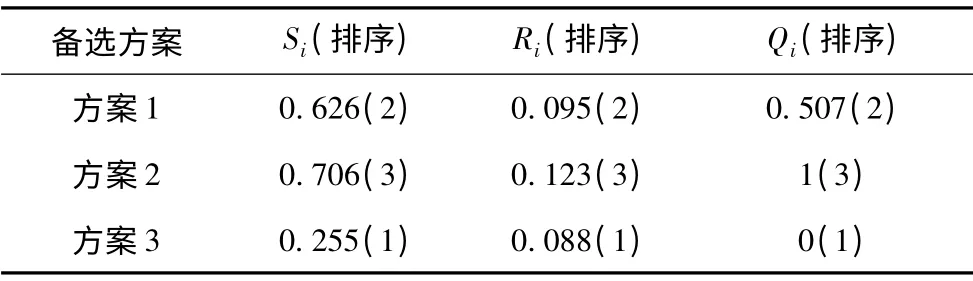
表4 备选方案排序结果Tab.4 Results ranking of alternatives

结合理想方案的选取条件，对备选方案的最优性进行验证:

根据评判准则可以得到，备选方案中方案3 综合表现最好，为最优方案，方案1 是次优方案，方案2的可选性相对较差。通过考虑群体效用的最大化与个体遗憾的最小化，得到的最优方案易于被决策者所接受。

4 结论

本文以微电网建设规划方案的评估与优化选择为背景，建立了DEMATEL-ANP-VIKOR 混合决策模型，对指标的相互关联性、指标权重分配和备选方案排序进行分析。研究表明，根据DEMATEL 法量化指标之间的相互影响程度，可有效实现指标体系中要素间关联关系的界定;结合指标要素关系的网络结构图，采用ANP 法得到的指标权重与层次分析法的计算结果相比其均衡性较高;最后利用VIKOR 法引入决策者的个人偏好得到优化选择方案，综合考虑了群体效益和个体遗憾的相对效果。研究结果对指标体系的设计、评价指标的改善和方案的优化选择具有一定的参考意义。

［1］ 韦钢，吴伟力，刘佳，等．基于SE-DEA 模型的电网规划方案综合决策体系［J］．电网技术，2007，31(24):12-16，27．

Wei Gang，Wu Weili，Liu Jia，et al．Comprehensive judgment for power system planning alternatives based on SE-DEA model［J］．Power System Technology，2007，31(24):12-16，27．

［2］ 赵媛媛，艾芊，余志文，等．考虑多种因素评估的微电网优化调度［J］．电力系统保护与控制，2014，42(23):23-30．

Zhao Yuanyuan，Ai Qian，Yu Zhiwen，et al．A microgrid optimal scheduling considering the assessment of various factors［J］．Power System Protection and Control，2014，42(23):23-30．

［3］ 李华，贺鹏举，景丽婷，等．基于RAGA-PPM 的电能质量综合评估方法［J］．电工技术学报，2013，28(S2):349-353．

Li Hua，He Pengju，Jing Liting，et al．The method of power quality comprehensive evaluation based on projection parsuit［J］．Transactions of China Electrotechnical Society，2013，28(S2):349-353．

［4］ 卢志刚，周雷，杨丽君，等．微电网规划评价指标体系研究［J］．电工电能新技术，2014，33(9):25-29．

Lu Zhigang，Zhou Lei，Yang Lijun，et al．Index system of microgrid planning evaluation［J］．Advanced Technology of Electrical Engineering and Energy，2014，33(9):25-29．

［5］ 陈奎，韦晓广，牛俊萍，等．基于AHP-DEA 模型的电网规划方案综合评判决策［J］．电力系统保护与控制，2014，42(21):40-46．

Chen Kui，Wei Xiaoguang，Niu Junping，et al．Comprehensive judgment for power system planning alternatives based on AHP-DEA［J］．Power System Protection and Control，2014，42(21):40-46．

［6］ 马丽叶，卢志刚，胡华伟．基于区间数的城市配电网经济运行模糊综合评价［J］．电工技术学报，2012，27(8):163-171．

Ma Liye，Lu Zhigang，Hu Huawei．A fuzzy comprehensive evaluation method for economic operation of urban distribution network based on interval snumber［J］．Transactions of China Electrotechnical Society，2012，27(8):163-171．

［7］ 赵书强，程德才，刘璐．结合D-S 证据推理的贝叶斯网络法在配电网可靠性评估中的应用［J］．电工技术学报，2009，24(7):134-138．

Zhao Shuqiang，Cheng Decai，Liu Lu．Reliability evaluation of power distribution system based on D-S evidence inference and Bayesian networks method［J］．Transactions of China Electrotechnical Society，2009，24(7):134-138．

［8］ 徐志勇，张徐东，曾鸣，等．基于ANP 的多层次模糊综合评价法的电网建设项目后评价研究［J］．华东电力，2009，37(3):488-490．

Xu Zhiyong，Zhang Xudong，Zeng Ming，et al．Application of ANP-based multilevel fuzzy comprehensive evaluation methods to post-evaluation for grid construction projects［J］．East China Electric Power，2009，37(3):488-490．

［9］ 王瑞莲，赵万里．基于模糊决策的城市高压输电网规划方案评价方法［J］．电网技术，2013，37(2):488-492．

Wang Ruilian，Zhao Wanli．A fuzzy decision-based method to evaluate planning scheme for urban high voltage transmission network［J］．Power System Technology，2013，37(2):488-492．

［10］ 杨琦，马世英，唐晓骏，等．微电网规划评价指标体系构建与应用［J］．电力系统自动化，2012，36(9):13-17．

Yang Qi，Ma Shiying，Tang Xiaojun，et al．Evaluation index system construction and application of microgrid planning［J］．Automation of Electric Power Systems，2012，36(9):13-17．

［11］ 周黎莎，于新华．基于网络层次分析法的电力客户满意度模糊综合评价［J］．电网技术，2009，33(17):191-197．

Zhou Lisha，Yu Xinhua．Fuzzy comprehensive evaluation of power customer satisfaction based on analytic network process［J］．Power System Technology，2009，33(17):191-197．

［12］ Ouyang Yuping，How-Ming S，Gwo-Hshiung T．A VIKOR technique based on DEMATEL and ANP for information security risk control assessment［J］．Information Sciences，2013，232:482-500．

［13］ 李金超，李金颖，牛东晓，等．基于ANP 的电网企业运营能力评价模型研究［J］．电力系统保护与控制，2011，39(19):37-43．

Li Jinchao，Li Jinying，Niu Dongxiao，et al．Study on the evaluation model for the power grid corporation operation ability based on ANP［J］．Power System Protection and Control，2011，39(19):37-43．

［14］ Zandi A，Roghanian E．Extension of fuzzy electre based on VIKOR method［J］．Computers ＆ Industrial Engineering，2013，66(2):258-263．

［15］ 林晓华，冯毅雄，谭建荣，等．基于改进DEMATELVIKOR 混合模型的产品概念方案评价［J］．计算机集成制造系统，2011，17(12):2552-2561．

Lin Xiaohua，Feng Yixiong，Tan Jianrong，et al．Product concept evalution based on hybrid model of advanced DEMATEL-VIKOR algorithm［J］．Computer integrated manufacturing systems，2011，17(12):2552-2561．

［16］ Rezaie K，Ramiyani S S，Nazari-Shirkouhi S，et al．Evaluating performance of Iranian cement firms using an integrated fuzzy AHP-VIKOR method［J］．Applied Mathematical Modelling，2014，38(21-22):5033-5046．

［17］ Liu Huchen，You Jianxin，Fan Xiaojun，et al．Site selection in waste management by the VIKOR method using linguistic assessment［J］．Applied Soft Computing，2014，21:453-461．